CSC2541HF 知识预备: Variational Auto Encoder
预备统计学和信息论知识
信息熵
信息熵这一概念要解决的问题时如何衡量 某个随机事件所包含信息的期望值. 理论上, 我们认为当某个随机事件 大概率发生 时, 该事件携带的信息量少, 反之则携带较大的信息量.
为了度量某个随机事件的信息量, 我们定义 信息函数 $I(p)$, 其中 $p$ 为该事件的发生概率. 基于上面的基本假设, 可知该信息函数需要具备如下的基本性质:
- 该函数应与 $p$ 成反比, $p$ 越大则 $I(p)$ 越小, 反之亦然.
- 必然发生的事件不具备任何信息量, 即 $I(p=1) = 0$.
- 独立事件同时发生所包含的信息量等于各自信息量的和: $I(p_1 \cdot p_2) = I(p_1) \cdot I(p_2)$
基于惯例, 我们将信息函数 $I(p)$ 定义为 $I(p) = -\log{(p)}$.
由此可知, $I(p)$ 用于表达一个发生概率为 $p$ 的随机事件发生后所产生的信息量, 即 不确定性. 若假设某个随机事件的概率分布为 $p$, 则其信息的 期望值 则为:
\[H(p) = \sum_{i}p_i (-\log{(p_i)}) = -\sum_{i}p_i \cdot \log{(p_i)}.\]即为信息熵, 它衡量 某个随机事件所包含信息的期望值.
信息熵理论的提出解决了 通信的最优前缀编码 问题. 关于这一问题此处不作详细介绍. 此处给出结论: 当信息函数为 $\log_{2}{(x)}$ 时, 信息熵即为编码信息所需要的最小比特数.
KL散度
K-L散度 (Kullback-Leibler Divergemce) 本质是一种 量化给定的两个概率分布之间差异 的方法.
在概率学和统计学中, K-L 散度可用于度量在 使用一个分布去近似另一个分布 时所损失的信息量.
任意给定两个分布 $p(x)$ 和 $q(x)$, 其 K-L 散度的计算方法为
也就是
\[D_{\mathbf{KL}}(p \Vert q) := \sum_{i}p(x_i) \cdot \log{\frac{p(x_i)}{q(x_i)}}\]同时不难看出: K-L散度不具备对称性, 所计算的 并非是 不同分布之间距离的度量.
如果我们将 $p(x)$ 和 $q(x)$ 分别视为 数据的原始分布 和 对数据的近似分布, 则 $p$ 和 $q$ 的 K-L散度 就是 数据原始分布和近似分布之间对数差值的期望.
似然函数和对数似然函数
假设随机变量 $x$, 因其作为随机变量服从于某个固定的分布具有概率结构, 因此可以使用刻画该分布的参数 $\theta$ 刻画它的随机性.
由此我们引入 概率 和 似然 的概念:
- 似然描述: 已知随机变量的值 (输出结果), 刻画该随机过程的参数 $\theta$ 取值的合理性. 它是给定一组观察数据值时, 概率模型参数的函数, 表示 这些参数使得观察数据值出现的概率, 一般表示为 $L(\theta \vert x)$, 它从 数据 的角度估计模型参数的好坏, 不涉及关于参数的任何先验知识或信念.
- 概率描述: 已知随机过程由参数 $\theta$ 所刻画, 在该前提下随机变量的不同值 (输出结果) 的合理性. 它是给定一组概率模型参数时, 观察数据值的函数, 表示 这些观察数据值由这些参数决定的概率模型所生成的概率, 一般表示为 $P(x \vert \theta)$.
由此可知, 在统计学和机器学习领域中, 似然函数可用于 模型的参数估计.
对数似然 (Log-likelihood) 是统计学中一种常用语估计模型参数的方法, 它就是似然函数取对数后得到的结果. 相比于直接使用似然函数, 对数似然函数关于未知参数的偏导数求解更容易.
ELBO和变分推断问题
此处我们只对变分推断问题和ELBO作简要介绍.
隐变量 (Latent Variables), 即 潜变量 或 隐藏变量, 指在统计学和机器学习中, 不可直接观测 但可以对观测数据产生影响的随机变量, 常用于对 未知因素 的建模.
假设 $x$ 为观测数据, $z$ 为一组建模了观测数据的隐变量. 在此为了确保一般性, 我们假设概率模型的参数也被视为随机变量, 包含在隐变量 $z$ 中.
由此, 我们接下来需要解决的问题即为一个 推断问题: 给定一组观测数据, 通过计算决定某个概率分布的参数/隐变量, 反向拟合这组观测数据的分布, 也就是找出使得后验概率密度
\[p(z \vert x) = \frac{p(x, z)}{p(x)} = \frac{p(x, z)}{\int p(x, z)dz}\]最大的变量族 $z$.
而在求解该优化问题中, 必须涉及到对 $p(z \vert x)$ 的计算.
而在实际应用中, 可能由于计算复杂度或积分无闭式解等问题导致直接计算后验概率密度不可行. 此时若仍要近似后验概率密度 $p(z \vert x)$, 就需要使用 变分推断.
变分推断的基本思想是: 既然无法直接计算后验概率密度 $p(z \vert x)$, 则可寻找一个简单的分布 $q(z)$, 用于 近似 这个后验概率密度. 也就是说, 要从候选的概率分布族 $Q$ 中选择出满足:
\[\min_{q(z) \in Q} \text{KL}(q(z) ~ \Vert ~ p(z\vert x))\]的分布 $q^{*}(z)$:
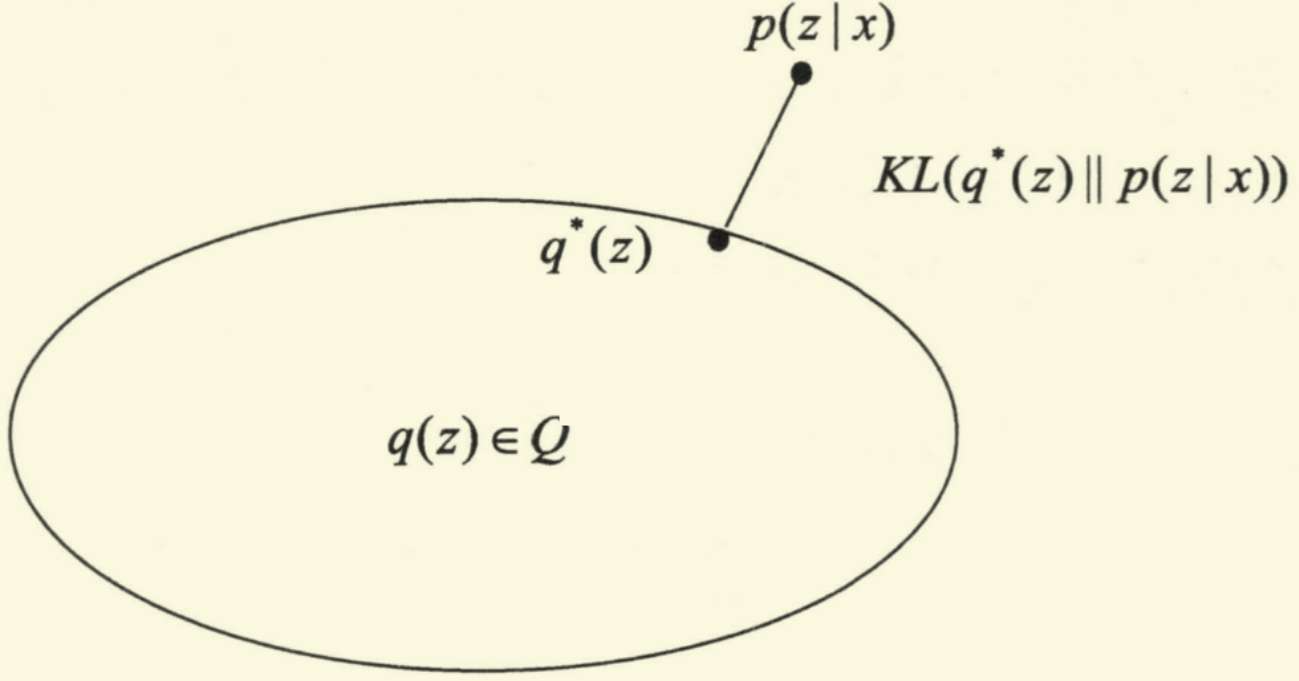
因此, 基于上述的想法, 需要对 KL散度:
\[\text{KL}(q(z) ~ \Vert ~ p(z\vert x))\]进行拆解:
\[\begin{align} \text{KL}(q(z) ~ \Vert ~ p(z\vert x)) &= \int q(z) \cdot \log{\frac{q(z)}{p(z \vert x)}} \\ &= \int q(z)\log{q(z)}dz - \int q(z)\log{p(z \vert x)}dz \\ &= \log{p(x)} - \{ \int q(z)\log{p(x, z)}dz - \int q(z)\log{q(z)}dz\} \\ &= \log{p(x)} - \mathbb{E}_q[\log{p(x, z)} - \log{q(z)}]\end{align}\]并且知, 由于 K-L散度非负, 故有
\[\log{p(x)} \geqslant \mathbb{E}_q [\log{p(x, z)} - \log{q(z)}]\]我们称不等式左侧式为 证据 (Evidence), 右侧则为 证据下界 (Evidence Lower Bound, 即 ELBO).
一般地, ELBO 记为 $L(q)$.
接下来, 求解目的即为 $q(z)$: 我们需要求解 $q(z)$ 从而最小化这个 K-L 散度. 由于 K-L 散度中 $\log{P(x)}$ 为常量, 因此要最小化K-L 散度, 问题转化为 最大化ELBO: $L(q)$.
总体上, 变分推断的常见步骤即为:
- 定义变分分布 $q(z)$.
- 推导证据下界:
ELBO的表达式. - 以最大化
ELBO作为优化目标得到最优化分布 $q^{*}(z)$, 将其作为无法直接求得的后验概率分布 $p(z \vert x)$ 的近似.
Auto Encoder
自编码器可被视为一个自动的, 试图还原其原始输入的模型. 常规的自编码器模型由 编码器 (Encoder) 和 解码器 (Decoder) 两部分组成. 编码器将输入 $x$ 转换为中间变量 $y$, 也就是 将输入数据的数据空间映射到某个隐变量 (latent variable) 所在的隐空间中. 解码器则接受中间变量 $y$ 作为其输入, 将其转换为输出 $\bar{x}$, 而优化目标则为: 让 $x$ 和 $\bar{x}$ 无限接近.
具体地说, 自编码器中的编码器将输入的高维数据样本编码为一个低维的隐向量, 该向量中的每个维度对应该样本的 某些 属性. 而解码器接受这样的 latent vector, 并将其从隐空间中重映射到原来的样本空间中.
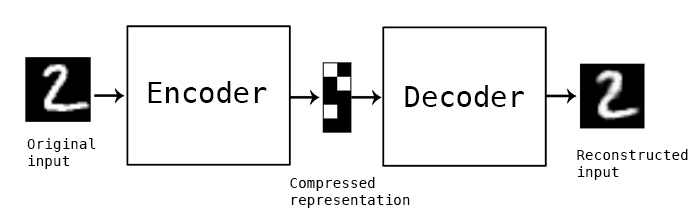
基本理念
本质上, 自编码器是一种 有损压缩 算法. 编码器可以学习到输入数据的隐含特征, 解码器则使用所学习到的新特征重构出原始的输入数据. 直观地, 自编码器是一种比主成分分析 (PCA) 更强大的特征降维方法.
自编码器的训练是 无监督 的. 在训练中, 自编码器神经网络会从数据样本中 自动学习 对输入的高维数据进行高效的特征提取和特征表示的方法.
由此我们亦可知, 自编码器是 数据相关 (data-dependent) 的. 由于自编码器在训练过程中只会接触训练数据, 它学习到的, 压缩和重构特征的方法仅限于和训练数据相似/相同的特征. 因此经过训练得到的自编码器只具有 压缩和重构与训练数据分布类似的输入数据 的能力.
自编码器的压缩也是有损的: 其解压缩的输出和原始输入相比是 退化的.
训练目标与损失函数的推导
自编码器的训练目标是是给定 输入数据, 求出输出的重建结果, 比对重建结果和输入数据之间的偏差, 然后对神经网络进行误差反向传播优化模型参数, 尽可能提升解码器重建所得数据的准确性.
由自编码器的基本结构可知, 构建自编码器需要设计 编码器, 解码器 并设计 损失函数.
Variational Auto Encoder
变分自编码器 (Variational Auto Encoder) 是一种生成模型, 希望从训练数据中建模训练数据的真实数据分布, 并反过来用学习到的数据分布去生成符合原分布的数据, 或者建模原分布.
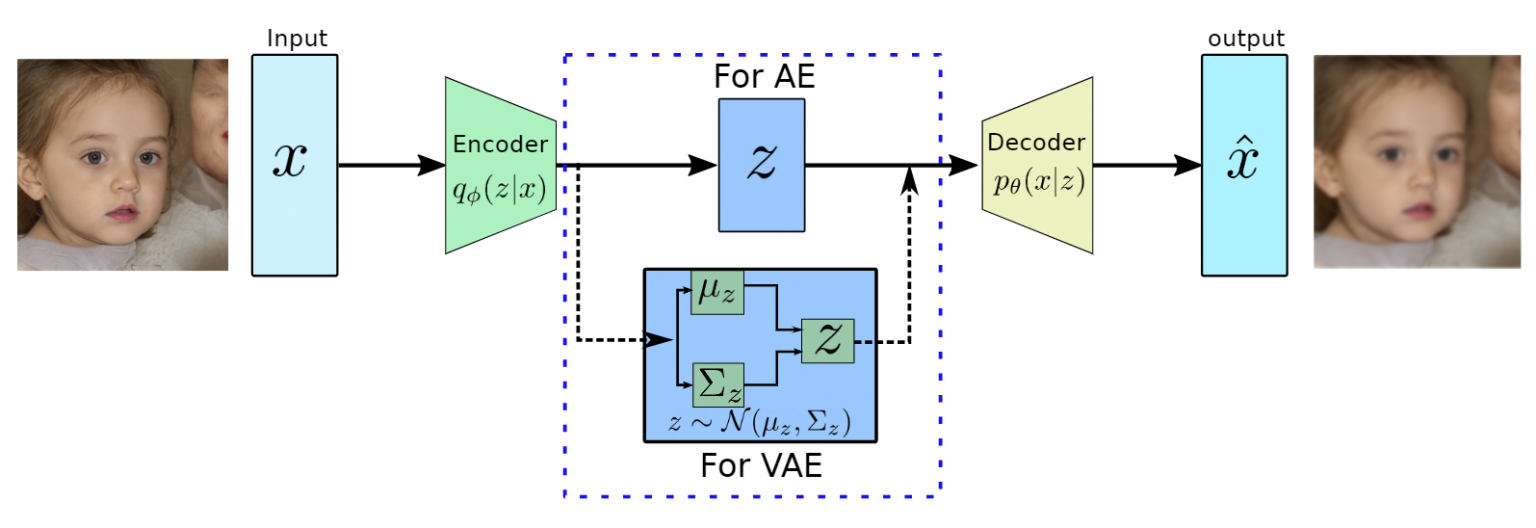
变分自编码器的网络结构和自编码器类似, 大致上均由编码器和解码器组成. 不同的是, 变分自编码器的编码器模块输出的是一个 多维高斯分布 的 均值 $\mu$ 和方差 $\delta$, 然后在由该均值和方差确定的多维高斯分布中采样得到一个隐向量 $z$, 再将其送入解码器中进行解码, 生成新的结果.
由此可见, 在架构上 VAE 允许同样的输入对应多个不同的输出, 并且希望这些输出之间尽可能类似. 相对的, 自编码器的输入和输出是 一一对应 的, 不具备生成新数据的能力.
基本理念
在理解变分自编码器的架构时, 重点是理解它是如何建模隐变量 $z$ 所服从的分布的. 为此, 我们假设隐变量的取值是和变分自编码器的输入 $x$ 取值相关的 ,也就是:
\[z \sim p(z \vert x)\]在本文上面的 “ELBO和变分推断问题” 一节中, 已经提到了后验概率 $p(z \vert x)$ 计算的困难性. 为了解决这一问题, 我们引入 变分推断 方法, 使用某个较简单的分布 $q(z)$ 拟合后验概率分布, 这也是 变分自编码器 其名中 “变分” 的来源.
训练目标与损失函数的推导
在确定了基本目标后, 可知一个粗略的目标是近似 $p(z \vert x)$ 和 $q(z)$. 显然我们可以使用 KL 散度衡量这两个分布之间的差异:
\[KL(q(z) ~ \Vert ~ p(z \vert x)) ~~ (*)\]随后对上述的KL散度公式变换如下:
\[\begin{aligned}(*) &= \int q(z) \cdot \log{\frac{q(z)}{p(z \vert x)}} dz \\&= \int q(z) \log{q(z)dz} + \int q(z) \log{p(x)}dz - \int q(z)log{[p(x \vert z) p(z)]}dz \\&= \log{p(x)} + \int q(z) \log{q(z)}dz - \int q(z) \log{[p(x \vert z) p(z)]}dz \end{aligned}\]可知: 由于 p(x)
杂记
Reference
https://mp.weixin.qq.com/s/KQUDz8cP95RQpHVl7TpaVA
https://blog.csdn.net/qq_27590277/article/details/129106904
https://blog.csdn.net/u010605984/article/details/140749144
https://blog.csdn.net/m0_51323388/article/details/134223701
https://blog.csdn.net/ttrr27/article/details/140731955
https://www.bilibili.com/read/cv33597441/
https://zhuanlan.zhihu.com/p/611373545
https://www.cs.princeton.edu/courses/archive/fall11/cos597C/lectures/variational-inference-i.pdf
https://zhuanlan.zhihu.com/p/650543717
