计算精度, 误差和数字表示法
本章将简述 数学建模 和 模拟 的基本目标, 并描述 精度, 误差 的一系列概念和计算方式, 并回顾计算机中二进制下的定点整数/实数表示法.
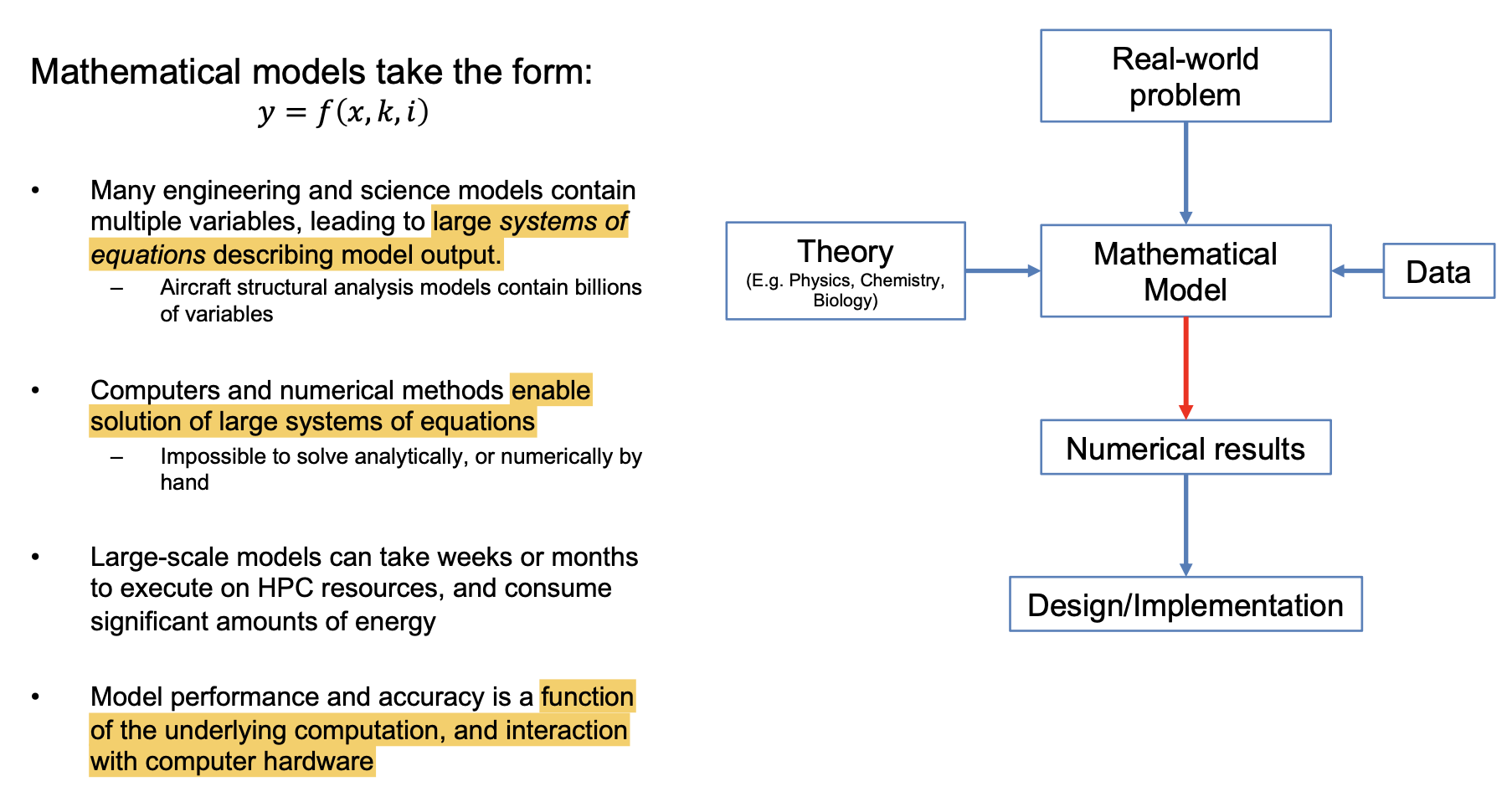
我们首先讨论数学建模的基本概念. 为了解决现实世界中的问题, 通过对问题本身的观察和分析, 将不同领域的理论, 定律和所收集的数据相结合, 所构成的模型就称为 数学模型, 而要基于数学模型解决问题, 就需要对问题进行 建模, 并执行运算或求解.
一般地, 数学模型具有下列的形式:
\[y = f(x, k, i)\]其中, 因变量 $y$ 代表数学模型 反映系统当前状态 的输出, 独立变量 $x$ 表示模型被计算和评估的不同维度, $k$ 为模型的可调参数, 而 $i$ 为我们向模型提供的输入.
为了实现对模型的计算和模拟, 往往需要实现复杂和大规模的计算, 为了实现这一目标, 就需要研究精度和误差控制, 数值分析方法和优化方法.
计算精度: 准确度和精确度
下面我们介绍数种常见误差的定义, 区分和计算方法.
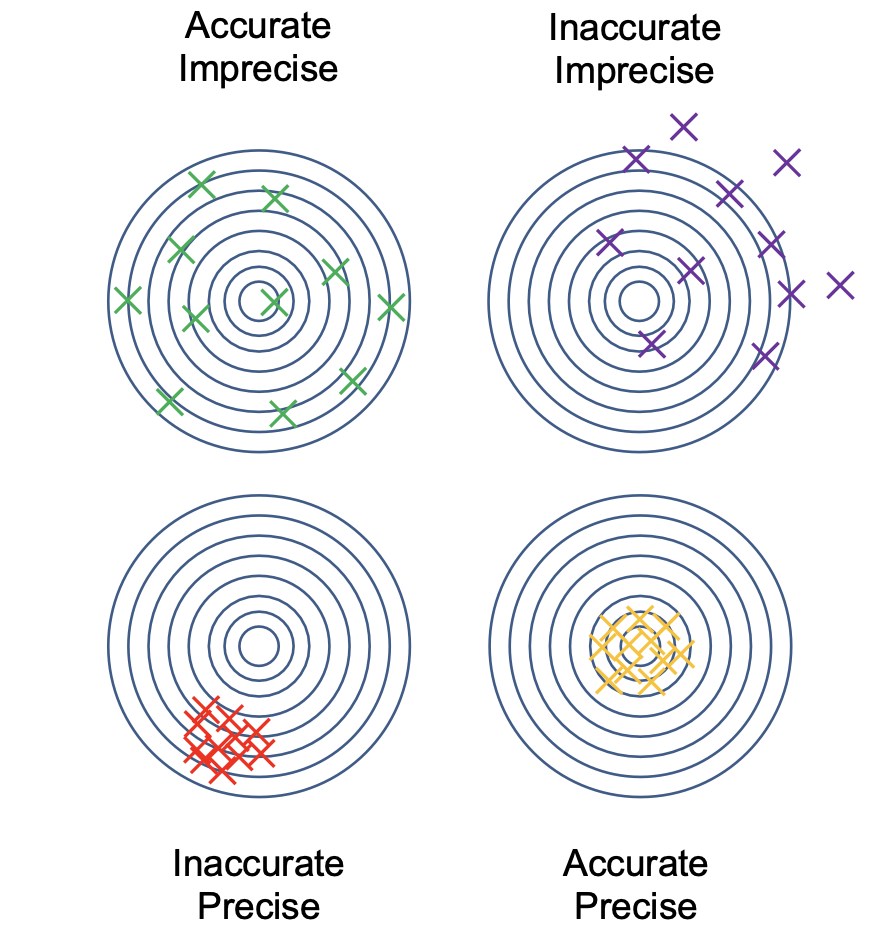
准确度和精确度 (Accuracy & Precision)
我们首先讨论准确度和精确度的概念.
准确度所定义的是: 所得到的计算结果从 总体上来看 距离真实值的偏差大小, 而精确度所量度的是所得到的全部计算结果的 离散程度 (How closely computed values agree with each other).
在表示误差 (Error) 时, 自然需要将准确度和精确度结合起来.
计算误差
下面介绍四种不同的误差定义: 绝对误差, 相对误差, 舍入误差和截断误差.
绝对误差 Absolute Error
任何计算上的误差都源于对 数学公式和计算结果的近似. 一般地, 在计算上的误差可被表示为:
\[\text{True value} = \text{approximation} + \text{error}\]而 绝对误差 的定义就是: 真实值 True Value 和近似值 approximation 之间的差别, 也就是:
值得注意的是: 绝对误差唯一考虑的是数值意义上的误差大小, 它并不将 “误差值大小相比近似值或真实值的百分比/占比” 考虑在内.
相对误差 Relative Error
相对误差所描述的是 误差值相对真实值的占比. 其计算方法是:
\[E_r = \frac{\text{error}}{\text{True value}}\]并表示为 百分比 的形式.

舍入误差 Round-off Error
舍入误差可以源于 “计算机对数值表示的精度有限” 这一客观限制, 也可以源于需要被表示的数值本身的性质, 如无理数或无限循环小数就不能被完整的表示, 只能取它有限长的一部分作为它的表示.
因而, 所取的那一部分表示和 理论上被表示数的真实值 之间的差别就被称为 舍入误差.
截断误差 Truncation Error
截断误差源于一些特殊的表示方法. 如: 若使用傅里叶级数或麦克劳林级数表示函数, 则会由于 表示法本身有无穷多项, 只能 截取 有限项而产生截断误差.

其他误差
此外, 在建模, 数据收集和处理过程中也可能引入误差: 例如所构建的模型并不是最优模型或并未考虑某些重要因素, 则会导致模拟的结果与真实情况产生较大的偏差; 在收集数据时, 由于测量工具本身存在的 系统误差 (Systematic Bias) 和测量过程中随机引入的 随机偏差 (Random Flucturations) 也会导致最终得到结果的误差的进一步加大, 在处理数据时人为犯错, 如单位转换或进制转换时出错, 也会引入误差.
数字表示
下面考虑数字表示. 在本课程中, 我们主要关注 二进制数 的表示.
整数表示法
整数可以表为无符号整数与有符号整数, 前者由于使用范围过于狭窄已不常见. 对于有符号整数, 目前主流的表示法为 实现简易, 计算方便 的 二进制补码表示法.
二进制补码表示法将最左侧的最高位作为 符号位, $0$ 表示正数而 $1$ 表示负数, 因此对于 $n$ 个二进制位, 表示范围是 $2^n - 1$ 到 $-2^n$. 同时, 满足 $\bar{x} + 1 = - x$, 因此对于使用补码表示的二进制数, 两数相减就转换为二进制加法计算.
定点实数表示法
确定可用于表示实数的二进制位数量后, 就可将二进制 bit stream 拆分为两个长度相同的部分表示实数: 左侧表示整数部分, 而右侧表示小数. 举例如下:

定点运算 Fixed Point Arithmetic

