光线追踪与辐射着色
本届我们讨论两种截然不同的, 渲染具有栩栩如生的光照的立体场景的方法: 建模光线并考虑光在场景中的传递路径与交互的 光线追踪, 以及将光视为 不同物体表面间的能量交换 的 辐射着色.
光线追踪 Raytracing
首先考虑对 光线 的建模. 一般地, 我们将光线建模为由 起始点坐标向量 和 方向向量 组成的 向量, 由此我们可使用这两个列向量表示任何一条光线.
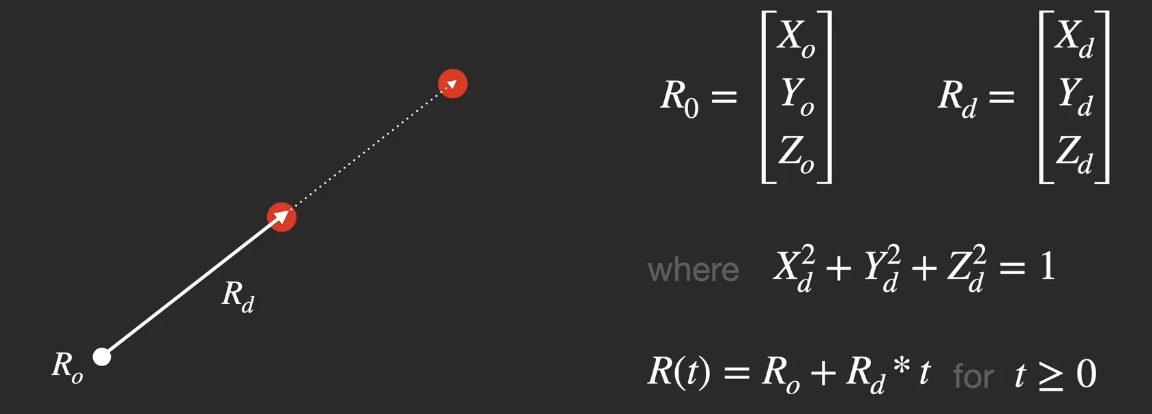
如上图所示, $R_d$ 是经过 归一化 后得到的, 指示光线传播方向的 单位向量, 通过控制参数 $t$ 我们可以调整光线的长度.
随后我们考虑: 什么是具有 “栩栩如生, 贴近现实” 的光影的三维场景. 从下面的图片中我们可以看出, 贴近现实的光影效果包括了 光的反射, 折射 (Reflection, Refraction) 和 透明或半透明物体的质感 (Transparency), 镜面反射的高光 (Specular Highlights), 阴影 (Shadows) 和 景深 (Depth of field).

值得注意的是, 上面提到的大多数真实光影效果都是 使用光线追踪技术模拟真实光影自然得到的产物, 而不像传统的光影模拟技术一样需要人为地 “分析和计算” 出阴影等.
下面我们考虑一个更简单, 更具代表性的场景, 讨论光如何在简化的场景中与物体交互.

考虑最简单的情形: 假设光源射出 一束光线 (虽然这在现实中不可能, 因为光线是人为定义的抽象概念), 它在空间中传播并打到物体的表面上, 并取决于物体本身的 BSDF 函数产生一系列的反射, 折射等效果.
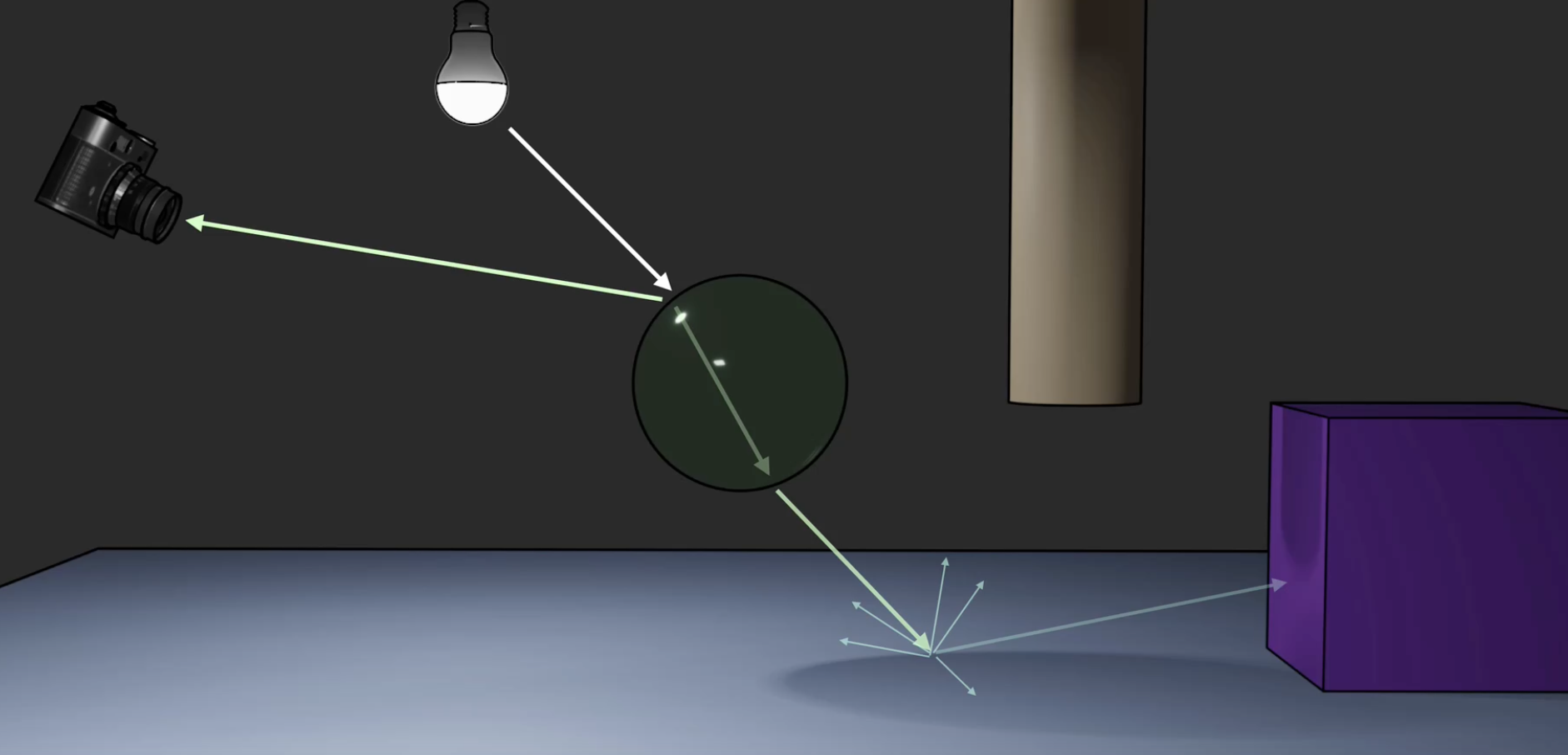
如上面的例子所示, 光源射出一束白光后, 经过场景中的传递打到绿色的玻璃球中, 一部分光线被绿色玻璃反射为射入视点 (也就是 Camera) 的绿光, 另外一部分经过折射穿透球体后射出, 打到 粗糙 的地面上同时发生漫反射, 少量光线发生镜面反射, 以很低的能量射到不透明的紫色块状物表面.
首先值得注意的是, 显然光源不可能只射出一束光线, 因此如果不做优化的话我们需要对大量的光线都进行建模. 比如下图的情形: 从光源射出的一束光直接打到光滑的障碍物上, 在反射一次后射出场景.
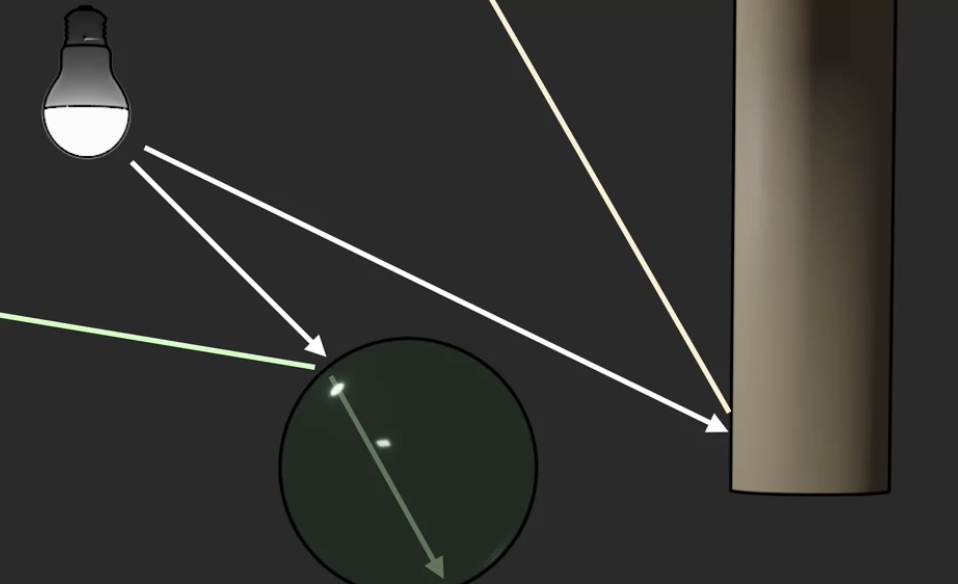
同时, 即便对于如此简化的光照模型, 在将光线追踪的执行过程转换为可用的算法时我们仍需要考虑一系列问题:
首先, 我们可以观察到光线和任何物体产生交互时都 可能发生反射和折射, 因此如果要建模光线的传播与交互, 所得到的就是类似 递归的树 一样的层级结构.
其次, 光线在任何物体上 漫反射 时会产生 大量的其他光线, 它们同样会在场景中传播并与物体交互, 因此如果不作优化的话, 随着我们对光线路径的推断, 我们所剩下的工作会变得 越来越多.
此外, 可以观察到, 在对光位于场景中的传播和与物体的交互进行建模的过程中, 如果从光源开始考虑每条发出的光线, 我们实际上建模了大量 最终并不会被视点捕获 的光线路径, 这些都是可以被省去的无效计算.
因此, 我们需要对光线追踪算法的执行步骤进行简化. 为了尽可能地避免无效计算, 我们将视点建模为 栅格化的视平面 (Viewplane), 然后从 视平面的每个像素开始, 反推所有 是从光源射出, 和场景中物体发生了交互, 并且最终射入了这个像素的光线.
称将 单独的一束光线射入场景 为 Raycasting. 如上一段所述的思路, 若从视平面的某个像素将光线射入场景, 考虑 这条光线在其传播路径上和场景中所有物体产生的所有交互, 就可确定这个像素的颜色, 并且可以提取出场景中诸如 物体之间的距离, 透视视角 (Perspective), 对视野的阻挡 (Occlusion) 等信息.
考虑下面的例子: 若要计算栅格化视平面上高亮位置的像素颜色, 我们从该像素出发, 从视点向这个像素射出一条 (实际上不存在的) 主光线, 在此处的例子中, 主光线首先打到了绿色的半透明球体上. ‘
注意: 在主光线打到任何物体上时, 我们自此要生成从 该物体被主光线打到的位置, 到 场景中任何可达到的光源 的新光线, 称其为 Shadow Feeler, 场景中有几个光源, 就应该有几条 Shadow Feeler. 不难看出, 这些 Shadow Feeler Rays 可以被用来计算场景中的哪些位置应该有 阴影:
如果某些从视平面像素出发, 经过物体的光线最终无法到达光源, 可认为它被 场景中的某些物体所阻挡, 因此这个对应的像素应该是相对昏暗的; 反之, 由于该光线最终可以达到光源, 我们可以认为在实际情况中确实存在这样从光源出发最终到达视点的光, 因此对应的像素应该是相对明亮的.
在给定的例子中, 由于场景中只有一个光源, 因此从视平面的像素上打出的主光线打到绿色的半透明球状物后, 生成的 Shadow Feeler Ray 恰好只有一条. 随后, 我们需要在光线传播树中 记录下这条信息, 关于这条光线实际的颜色将会在完成对场景中所有可见光线的分析后, 反着从光源出发再去分析光线打到了哪些物体, 根据不同物体的不同 BSDF 确定最终射入像素的颜色应该是什么.
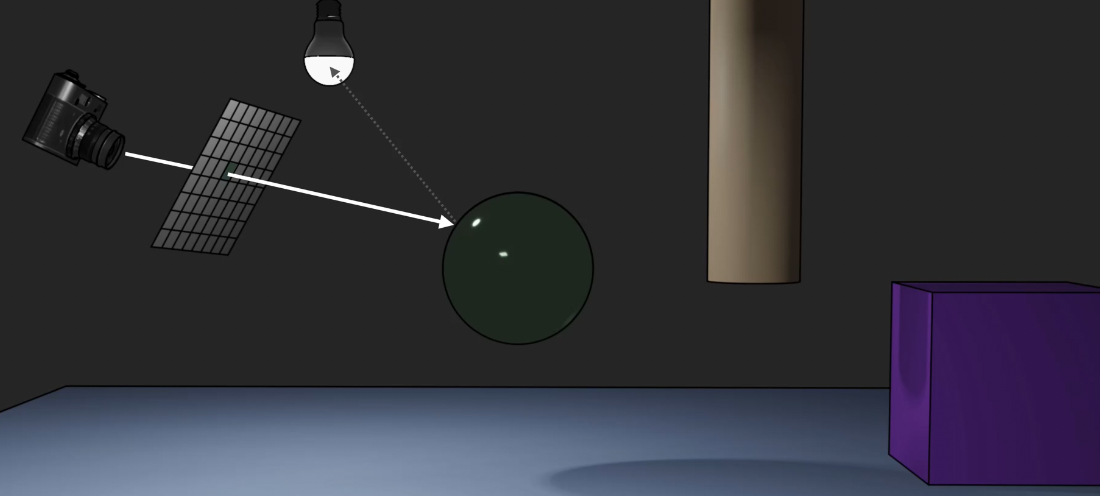
随后, 我们考虑在光线经过球体的折射, 在这个中空球体内部的传播情况. 由于随后经过折射的光线会打到球体的内表面, 因此在光线和球体内表面的交汇点上同样需要生成与这条被折射后的光线对应的 Shadow Feeler, 同样仅为一条.
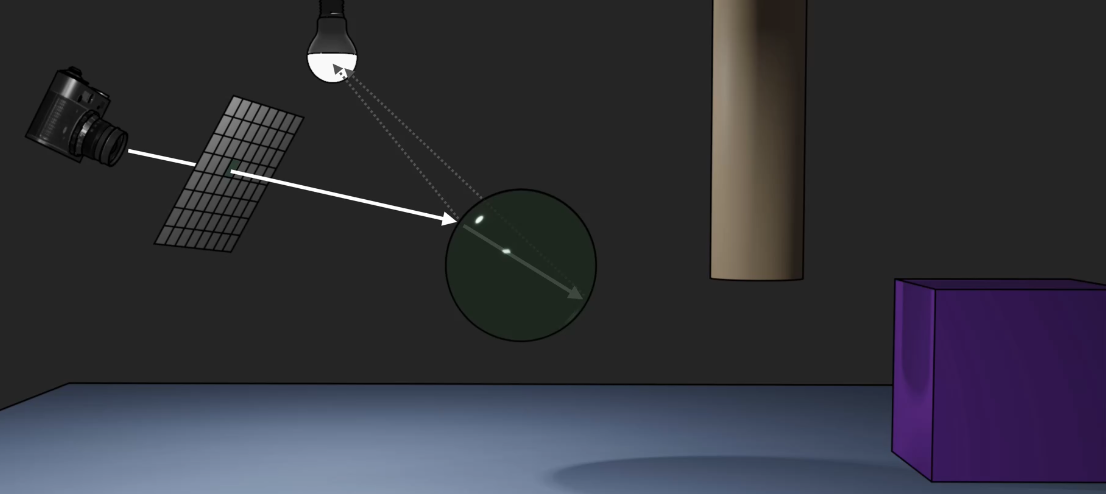
除此之外, 打到球体内表面的光线还可能在球体内部发生 内反射 (Internal Reflection), 但我们此处不予考虑这些复杂的光影效果.
最后, 光线穿过球体外壳继续传播, 打到紫色物体的表面. 同样我们构造关于 打到紫色物体表面的这束光的 Shadow Feeler. 由于这束 Shadow Feeler Ray 被墙阻挡, 无法到达光源, 因此我们对这束光的追踪到此为止, 同时可知紫色物体的表面对应位置应该有阴影存在.
随后, 我们对栅格化视平面上的其他像素也作同样的分析, 就可同样得出它的颜色应该是什么. 由此, 我们就对这个视平面完成了光线追踪任务.
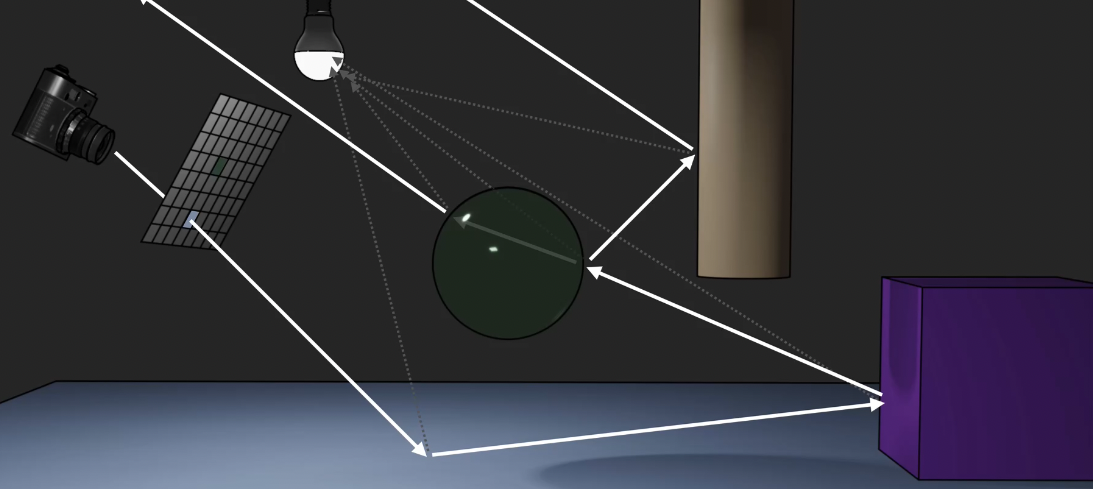
一般地, 我们会认为光线在传播过程中和不同物体的每一次交互都会带来一定的 能量损失, 因此会设定光线和物体追踪的 次数限额: 如果光线的能量耗尽或它在场景中超过了和物体交互的次数限制, 我们就会停止对这束光线的追踪.
但我们仍需考虑漫反射带来的 “光线数量爆炸” 的问题. 一种简单粗暴的解决方式是完全不考虑漫反射: 将物体的表面都认为是光滑的, 光线在表面上只发生镜面反射, 而不发生漫反射, 从而无需考虑漫反射引入的更多光线. 这一偷工减料的手段带来的负面效果是: 整个画面都会显得过于明亮, 甚至过曝, 无法生成 Soft diffuse surfaces 或 Soft Shadows.
以上就是 Classic Whitted Style Reverse Recursive Ray Tracing 的基本工作原理.
辐射着色 Radiosity
和传统的光线追踪一样, 辐射着色也属于计算机图形学中的过时技术, 但它的基本思想非常有趣. 在光线追踪方法中, 我们将光建模为 抽象的, 有方向但没有厚度 的向量, 辐射着色将光视为 不同物体表面之间的能量交换.
和光线追踪的长处恰好相反, 辐射着色不擅长于渲染透明物体或镜面反射, 但非常适合渲染粗糙的表面以及漫反射产生的光影.

辐射着色在渲染场景时关注的问题是: 场景中 不同物体表面的块 (Patches) 上的颜色和光影效果. 如下图所示, 若将场景从逻辑上切分为多个区块, 则对每个这些粗糙的区块都需要考虑它的光影效果.

在使用光线追踪技术渲染的场景中, 光源并不需要在场景中有对应的物理表示 (Physical Representation). 但对于辐射着色, 光源和其他物体无异, 被同样建模为多边形 (或多边形的组合). 唯一的不同是: 光源会 从自身发散光能 (Emitting their own light energy).

辐射着色利用了 热动力学 (Thermaldynamics) 中对稳态的计算思想: 能量平衡原则 (Energy Equilibrium). 给定的场景具有一定的能量, 这些能量在场景中的物体之间互相发生热传递, 直到达成稳态 (Steady State) : 物体之间不再发生任何热传递, 为止.
所谓的 Radiosity 或 Radiance (辐射), 就是指从某个位置 $X$ 离开物体表面的 粒子流 (Flux), 而 Irradiant (辐照) 则具有其他来源, 射到物体表面的位置 $X$ 的粒子束.
显然, 在计算机图形学的考虑范围内, 我们宿管新的粒子流只有 光子流, 换言之就是光.

自然, 对每个物体而言, 它表面的每个部分和外部环境进行的能量交换, 也就是它的 辐射 和所受到的 辐照, 都不是常量, 而会随着环境状态而改变, 这也是为什么在 Cornell Box 场景中, 方块表面的颜色并不是纯色的原因, 因为它和场景中的不同其他物体之间发生了值不尽相同的能量交换.
由此, 在辐射着色流程中, 对任何物体而言, 它表面的任何一块上都会有不同的能量交换状况. 同时, 因为处理的特性, 每一块上的颜色都会是 相同 的, 因此无论是出于严谨考虑还是视觉效果考虑, 辐射着色都需要将场景中任何物体的表面 分划为多个块, 并对这些块分别处理. 在实际情况中, 我们往往需要将整个场景的每一个平面上分划为 大量的小块 (Patches), 以满足对视觉效果的需求.

考虑下图所示, 仅涉及两个平面: $A_x$ 和 $A_{x’}$ 间的能量传递.
能量在表面 $A_x$, 以位置 $x$为中心的一小部分平面 $\delta A$ 和 表面 $A_{x’}$, 以位置 $x’$为中心的一小部分平面 $\delta A’$ 之间传递:
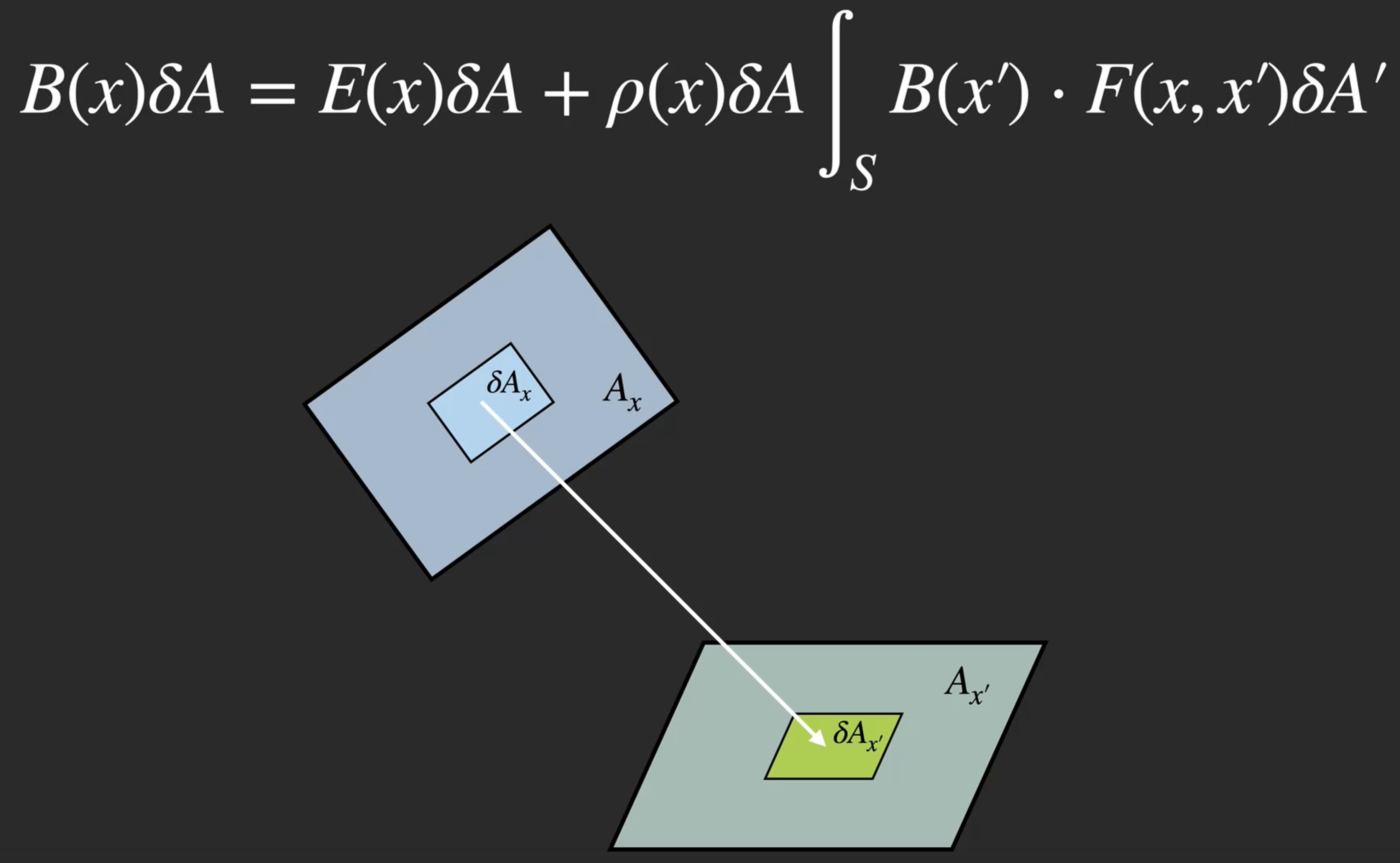
在式子中,
\[B(x)\delta A\]指从表面 $A_x$ 上, 以位置 $x$为中心的一小部分平面 $\delta A$ 辐射到平面 $A’$ 上的所有能量. 这些能量由两个部分组成. 首先是:
\[E(x)\delta A\]指 全部从这一片小区域中直接辐射出的能量, 而
\[\rho(x)\delta A\int_{S} B(x') \cdot F(x, x') \delta A'\]则是它所反射的 全部从场景中的其他物体那里所接收的能量, 其中 $\rho(x)$ 为点 $x$ 的 单位面积能量反射率 (Reflectivity), 因此 $\rho(x)\delta A$ 表示从场景中其他任何表面块 (Patches) 所接受的能量 总和.
$S$ 表示对变量 $x’$ 关于 整个场景 作积分, $F(x, x’)$ 表示这两个点之间的 Form Factor, 定义为: 当两个点 完全互相可见 时为 $1$, 反之为 $0$.
和渲染函数一样, 能量辐射方程同样由于关于 $x$ 递归而无法直接计算. 为了让辐射方程在计算上可行, 我们需要对它进行一定的 简化.
首先, 我们 不再关于场景中所有平面上的所有无限个点 $x’$ 做积分, 而是在将场景中所以平面分划为多个块 (Patches) 后, 对这些块求和:

注意 $\rho$ 是反射常数, 而 $B_i$ 就是辐射率 (Radiosity).
在实践中, 这一优化方式意味着我们需要进一步地对场景的多边形网格 栅格化, 直到表面的区块被划分得足够小, 以至于 可以用一种单独的颜色表示 为止.

就此, 我们就得到了 离散化 的辐射模型.
在将辐射方程离散化后, 我们就可使用雅可比迭代法 (Jacobi Iteration) 或高斯-赛德尔迭代法 (Gauss–Seidel method) 等数学工具近似计算仍具递归性的离散化辐射模型 (本质是一个复杂的线性方程组).
但是, 这仍需要大量的计算资源. 注意到这一步我们尚未在方程中引入 视点 (Viewpoint), 这是因为辐射是 空间特定 的, 而光线追踪是 视角特定 的: 一旦视点或视角发生变化, 光线追踪模型就需要重新计算, 而空间中的辐射不会随着视点或视角的变化而发生改变.
因此, 这意味着我们只需对场景中的辐射模型进行一次计算, 就可将计算的结果应用在场景里任意多种不同的视角上, 由此实现实时渲染.
此外, 我们还可以直接将对辐射的计算结果 写死到纹理贴图 (Texture) 中, 然后在渲染时直接将物体连同这个纹理一起渲染.
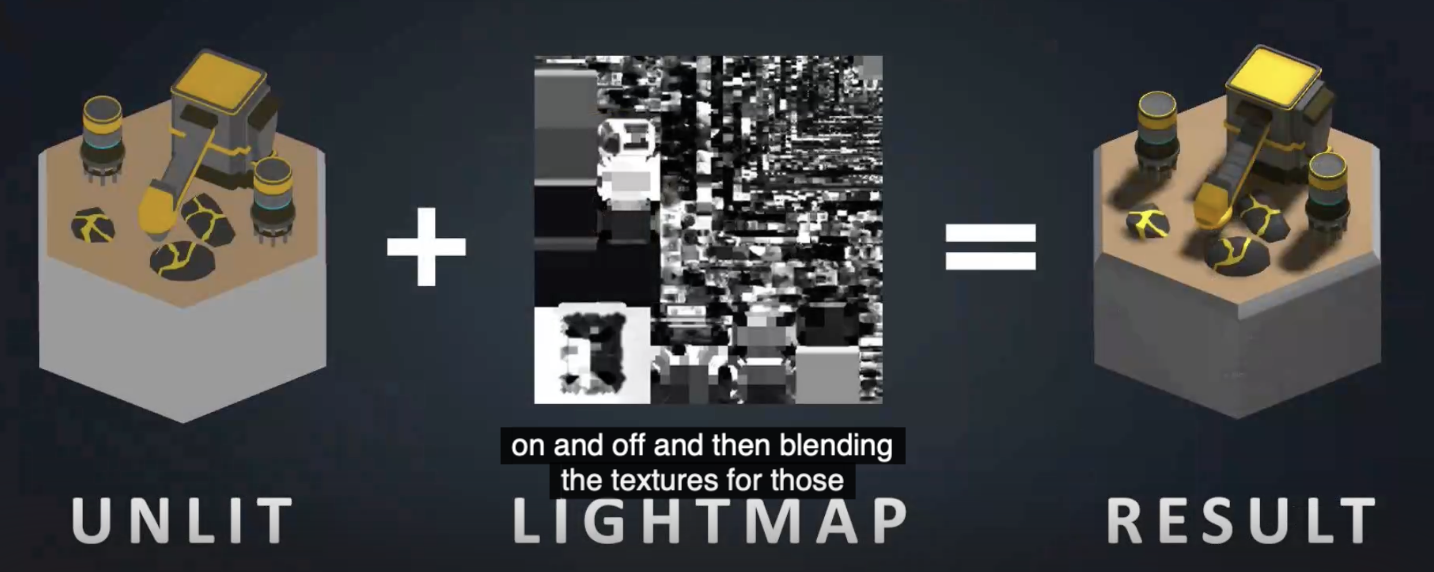
最后紧急补充:
注: specular reflection是specular highlight产生的原因, 后者是前者的效果.
并且注意: specular reflection (specular highlight) 是viewpoint dependent的, 因此不适合被texture baking.
什么是viewpoint independent? 如果某种效果或者技术的运算结果即便随着视点位置的变化也不会使视觉效果变得不真实, 则称它为 viewpoint independent.
有如下结果:
viewpoint dependent: ray tracing, path tracing, direct volume rendering, proxy geometry (splatting)
viewpoint independent: radiosity, the rendering equation, texture baking, marching cubes
