分布语义学
本章我们讨论分布语义学的相关定义和模型.
基本概念和相关定义
在自然语言处理任务中, 一项至关重要的任务是: 如何让计算机 “理解” 给定上下文中字词的 含义, 这个步骤被称为 语义处理 (Semantic Processing).
而分布语义学就是用来完成 语义处理 步骤的一种方法. 它基于下面的几个假设组成的 分布假设 (Distributional Hypothesis):
- 单纯依赖字词出现的上下文 即可推断出它的含义.
- 在类似的上下文中出现的字词共享 相似的含义.
- 字词的特征由它在上下文中的出现位置附近的其他字词刻画.

换言之, 分布假设认为, 文本的 上下文信息 就 足够形成 对某个 语言项目 (Linguistic item, 如字词) 的表示.
分布语义学模型的基本思想
分布语义学模型的基本思想是:
- 构造 高维特征向量 (
High-dimensional feature vector) 来描述某个语言项目. - 语言项目间的 语义学上的相似性 由 特征向量的相似程度 所刻画.
注意: 此处提及的 语言项目 是一个正式的语言学名词, 它用于指代 语言中任一个层次中的一个或一组单位, 如字词, 句子, 文本片段, 段落等.
为了描述语言项目所构造的高维向量所处的空间被称为 语义空间 (Semantic Space), 也称 嵌入空间 (Embedding Space), 潜在表示空间 (Latent Representation Space).
在语义空间中, 我们考虑 高维特征向量 的 相似性 和 差异性. 它们分别由 距离函数 (Distance Function) 和 相似函数 (Similarity Function) 所刻画:

而常用的距离函数和相似函数分别是 欧氏距离 和 向量内积或向量余弦距离:

最简单的分布语义学模型
最简单的分布语义学模型使用 向量空间模型 (Vector Space Model) 和 字词权重计算 (Term Weighting) 编码特征向量.
向量空间模型, Vector Space Model
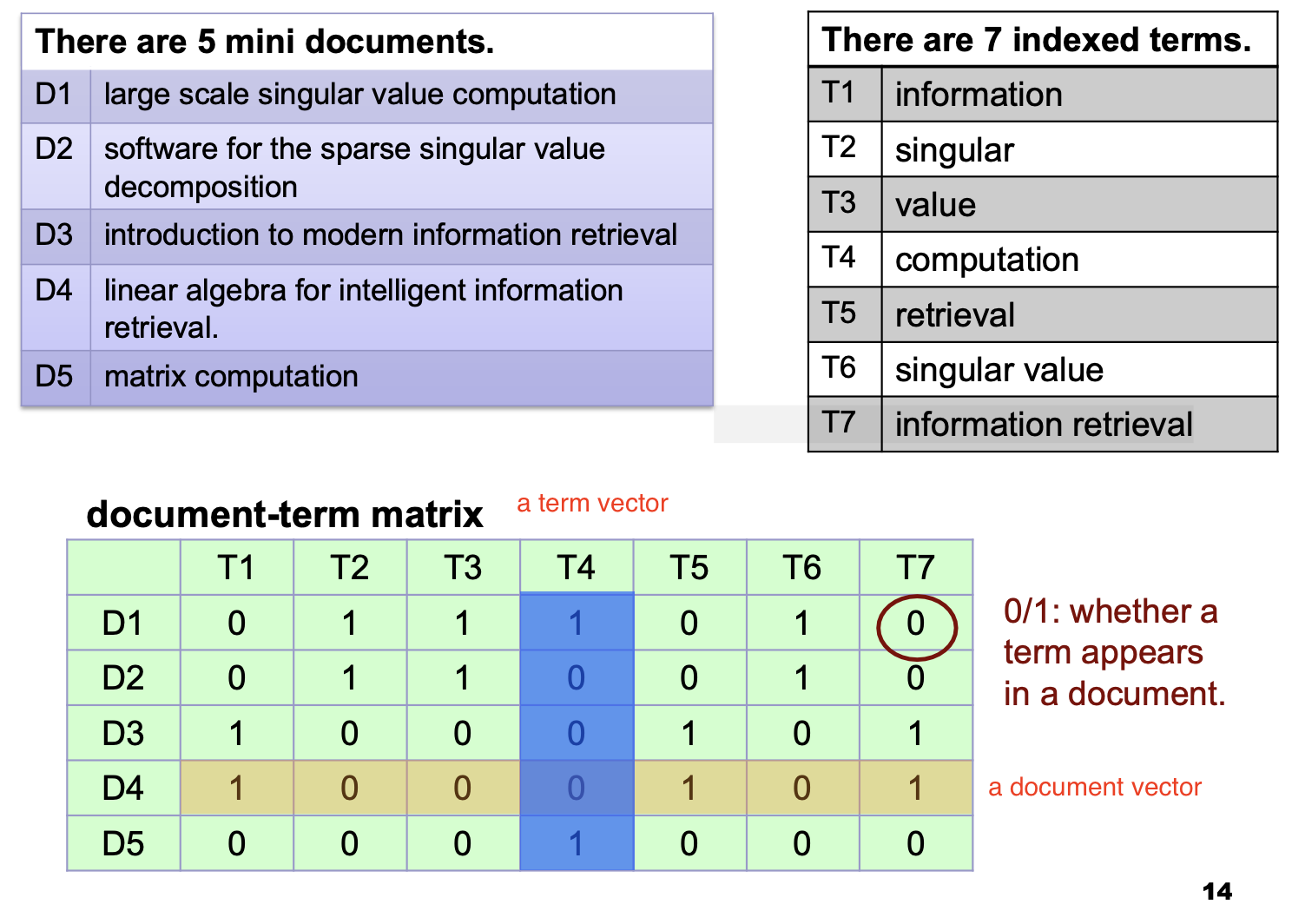
向量空间模型基于 对字词出现次数的统计 (Count based), 是将一段文本个体 (a piece of text object)表示为 存储由一系列预先给定的索引项的出现次数的高维向量 的 代数模型.
我们称涉及的 “一段文本个体” 为 文档 (document), 描述文档的高维向量称为 文档向量. 在文档向量中, 每个维度对应一个索引项 (Index Term) 在相关文档中的 出现次数.
显然, 如果对语料库中的每篇文档都统计和收集它们的文档向量, 我们最终就会得到 文档频数矩阵 (Document Frequency Matrix).
字词权重计算
下面考虑对 字词权重的计算 (Term Weighting). 一般地, 在进行计算时我们考虑下列的三个因素:

其中, Binary Weighting 就是一个可能取值为 $0$ 或 $1$, 表示 这个字词是否在文档中出现 的指标:

而 Term Frequency 词频和 TF-IDF 的定义就不再赘述:


基于向量空间模型的字词相似度计算
下面我们考虑如何 基于向量空间模型 计算 字词的相似度.
显然, 首先需要使用向量空间模型构造相关的 Word Vector. 然后, 就可以使用 某种描述向量间相似程度的测度, 比如 向量的余弦相似函数, 计算 Word Vectors 之间的相似程度.
而两种常规的构造 Word Vector 的方式是: 基于文档的方法 和 基于上下文的方法.

基于文档的方法
该方法基于 文档频率 的统计构造 Word Vector.
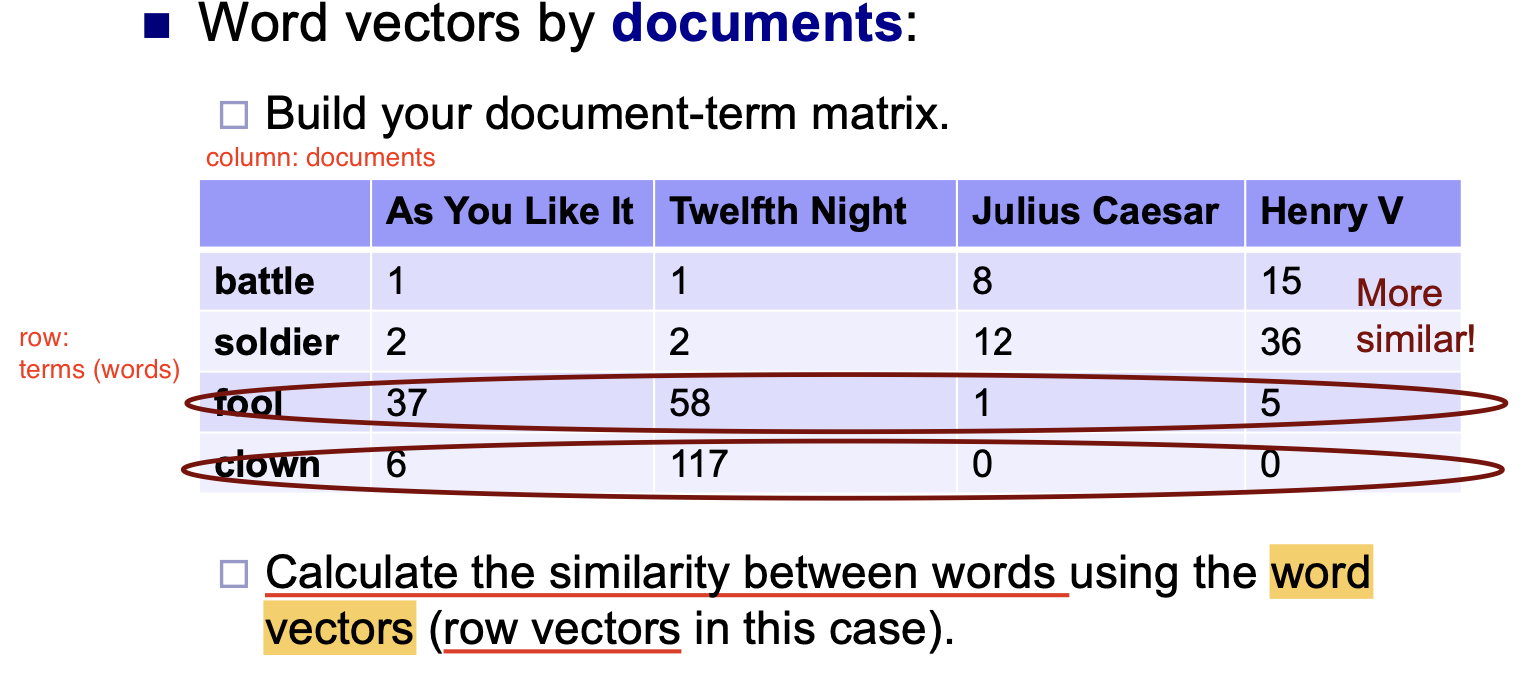
基于上下文的方法
该方法基于对 给定单词表中每个单词, 不同项 (Term) 的解释文本中出现的次数 构造 Word Vecor.

进一步地, 对包含目标字词的文本的选择有多种方式:
- 选择包含目标字词的 整个文档.
- 在文档中, 以目标文本为中心, 以某个窗宽为范围内的所有单词.
- 在文档中, 以目标文本为中心, 以某个窗宽为范围内的所有 具有实际含义 (如: 不为
Stop Word) 的单词.
注意此处窗宽一般有两种选择: 或者选定一个 很大 的窗宽, 或者选择一个 更小的 窗宽:

对文本的选择过程也就是所谓的 Context Engineering.
基于奇异值分解的稀疏向量转化
在生成 Word Vector 时, 不难注意到一个问题: 基于上下文方法和向量空间模型所生成的 Word Vector 实际上是 稀疏向量: 它们具有很大的维度, 但向量中绝大多数的维度上都为 $0$.
由于稀疏向量和稀疏矩阵一样, 在计算和存储上都存在效率不高的问题, 我们需要将 Word Vector 降维.

此处我们介绍一种常用且有效的数据降维方法: 基于 矩阵奇异值分解 的 潜在语义索引 (Latent Semantic Indexing).

通过矩阵奇异值分解, 可将规模庞大的文档矩阵 (Document Matrix) 分解为三个较小的行列式的 乘积. 此处还有下列的结论:
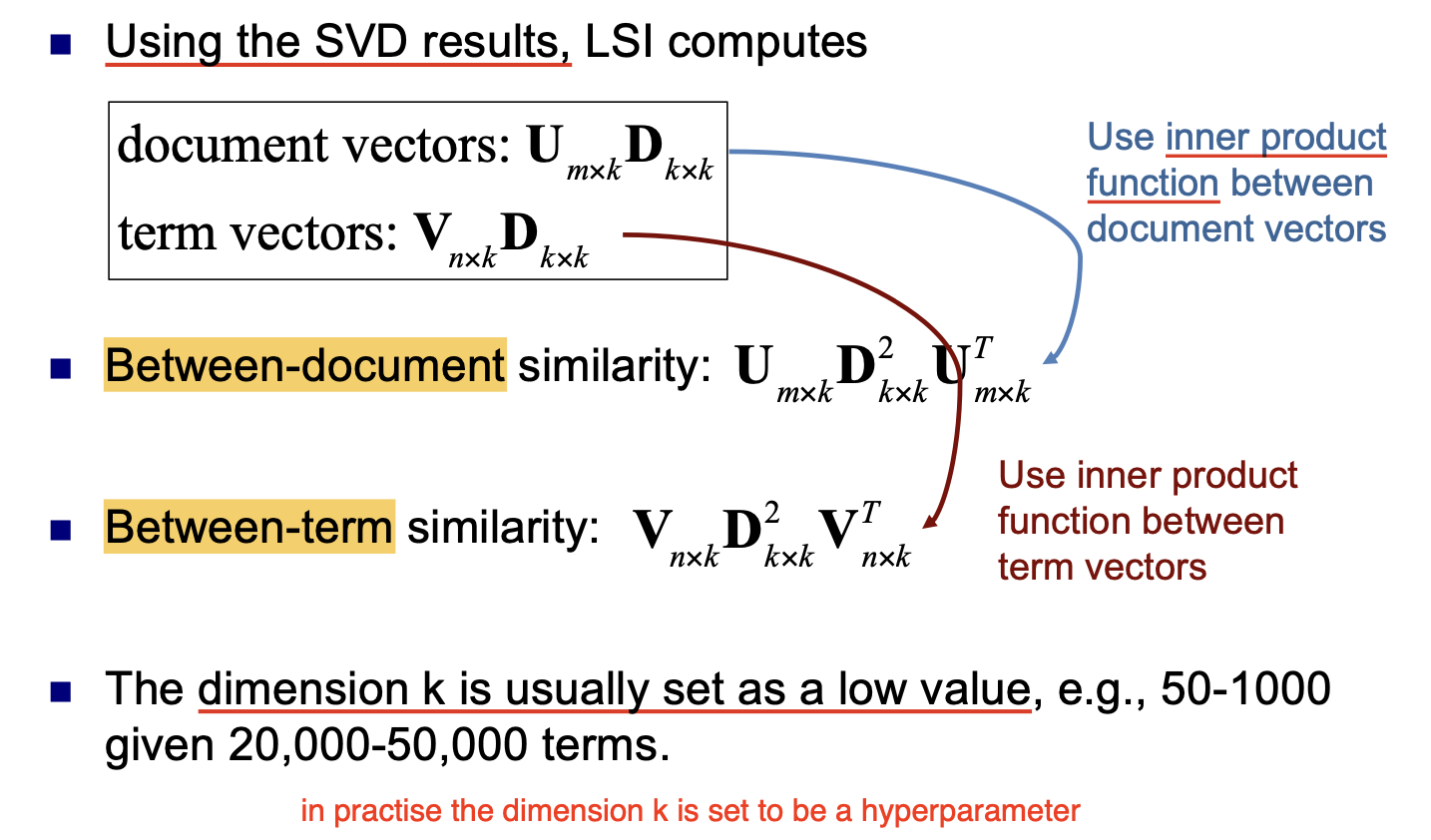
注意 Document | Term Vector 的表示方式.
这里使用的奇异值分解可被 单独视为一种通用的数据降维方法:

预测性的词编码 (Predictive Word Embedding)
预测性词编码模型的主要任务是: 基于 单词的出现信息, 如 “在目标词对应的内容文本中, 某个另外的词出现了多少次”, 或 “某个词是否在目标词对应的内容文本中出现过”, 对单词本身的含义进行预测.

我们可以使用词典中关于文字本身和其所处上下文的信息作为模型输入的一部分, 对模型进行训练. 下面我们介绍三种典型的预测性词编码模型: 连续词袋模型, Skip-Gram 和 GloVe.
连续词袋模型和 Skip-Gram 模型
连续词袋模型和 Skip-Gram 模型同属 Word2Vec 类的模型: 为了将文字转换为可被计算机处理的形式, Word2Vec 类模型将 词映射到实数域上的向量, 而这个从词到向量的过程被称为 编码 过程, 也就是 Word Embedding.
连续词袋模型
连续词袋模型使用上下文的信息预测中心词, 它既可被训练为 给定上下文信息预测中心词到底是哪个, 也可被训练为 给定上下文信息, 对中心词基于其词性进行分类. 它的处理管线主要由稠密化编码和 Logistic Regression 分类器组成.
连续词袋模型的输入被编码成 One-Hot 向量, 下图中的 $V$ 为词典 (Vocabulary) 中的总词数.
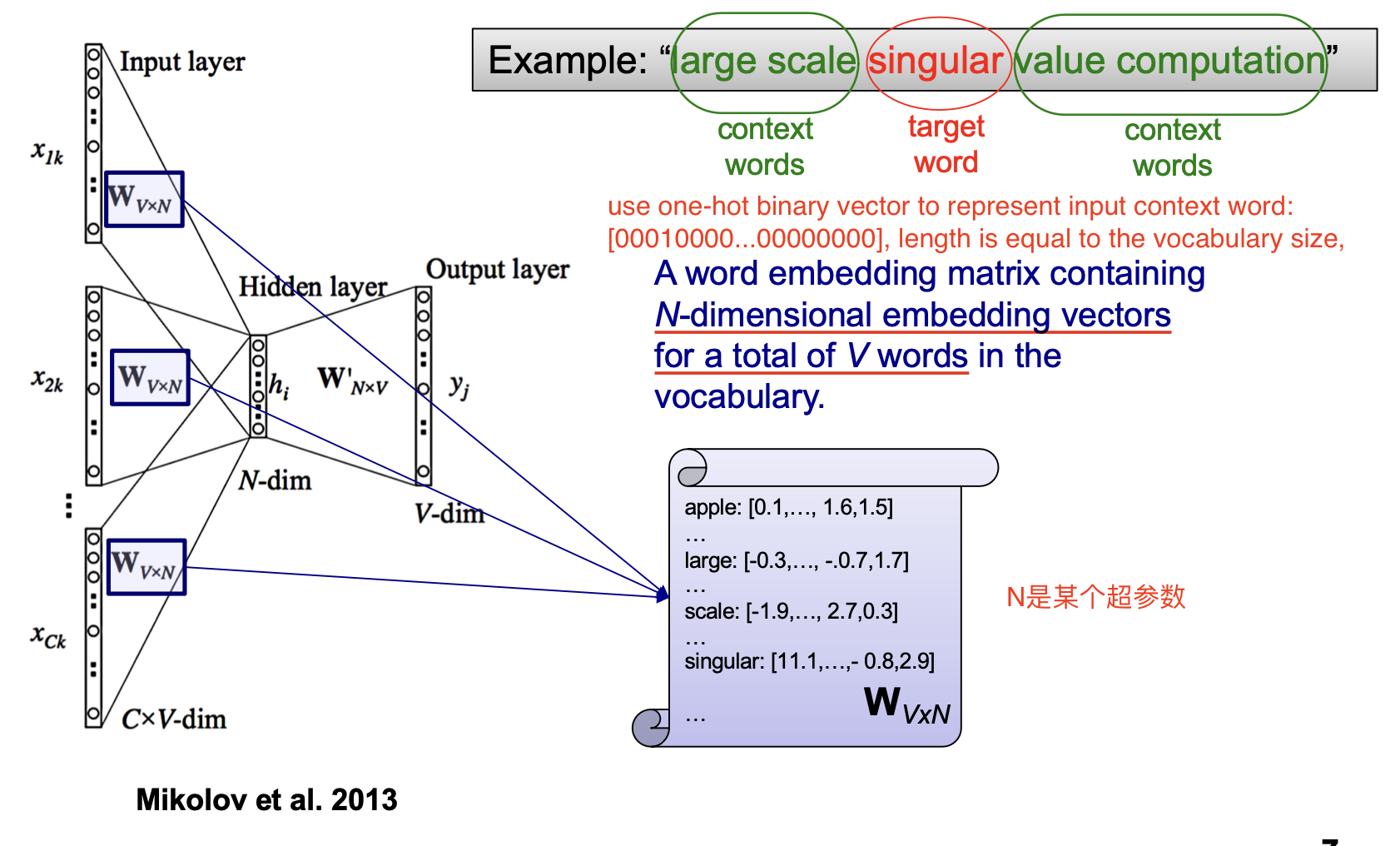
作为输入的 One-Hot 向量经过中间维度为 $V \cdot N$ ($N$ 为超参数) 的压缩矩阵后被压缩为只有 $N$ 个元素的向量 $h$. 也就是:
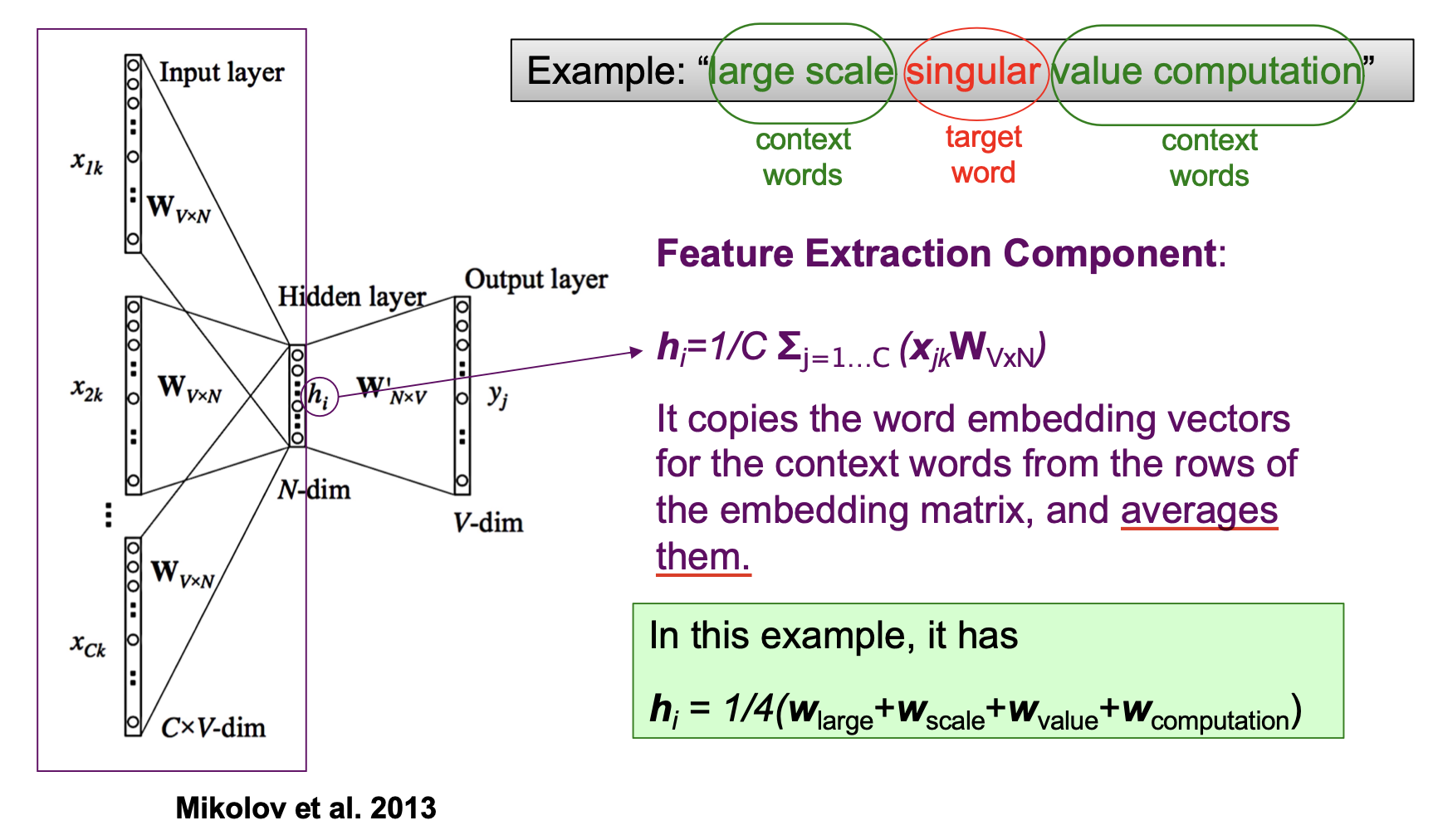
这是为了实现使用 由多个词组成的上下文 预测目标词的目的, 因此使用了 上下文词向量的平均.
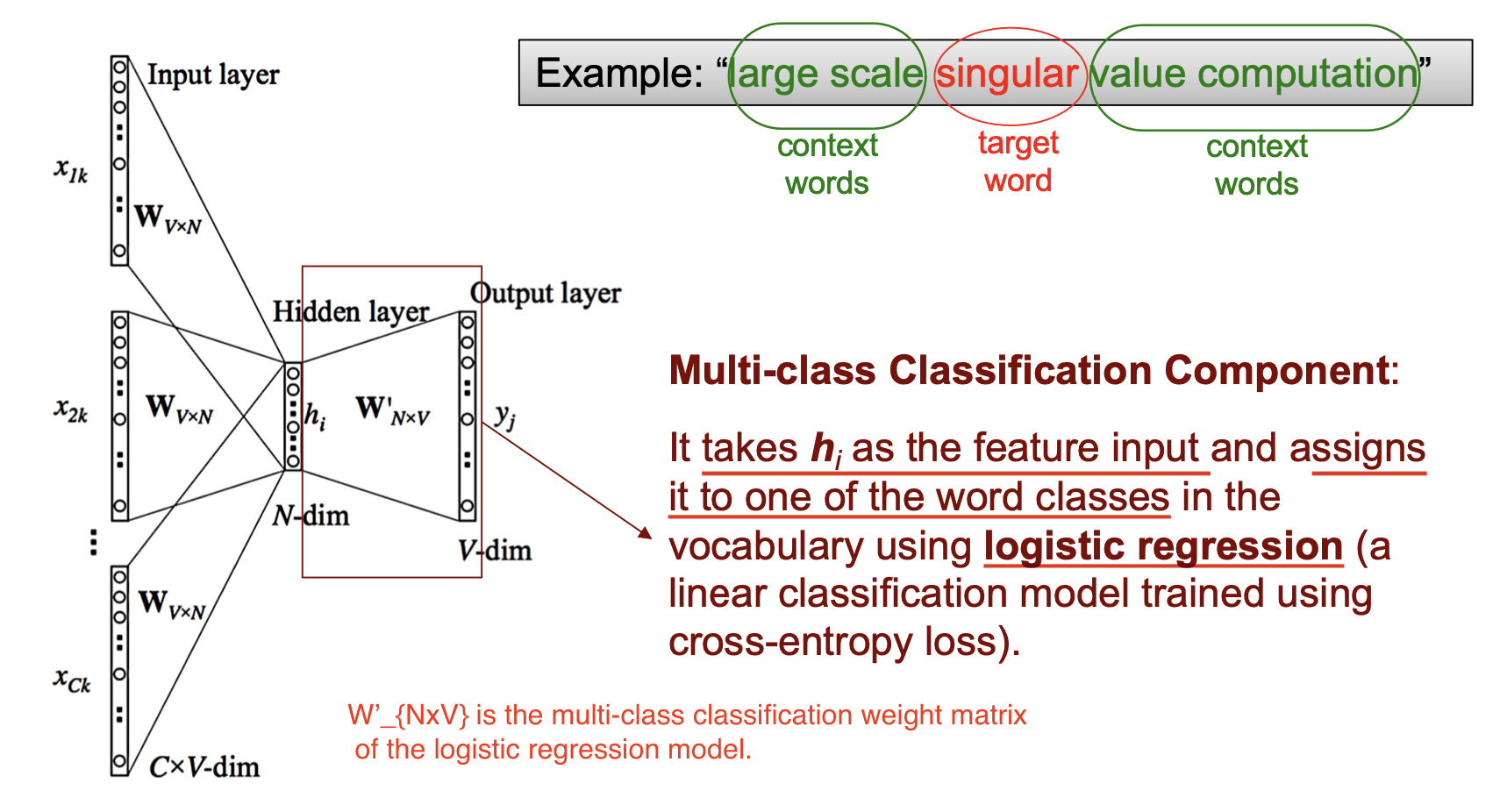
随后经过 Logistic Regression的权重矩阵 $W’$ 并使用 Sigmoid 函数得到概率形式的输出, 取最大概率对应的类, 这就是模型的预测结果.
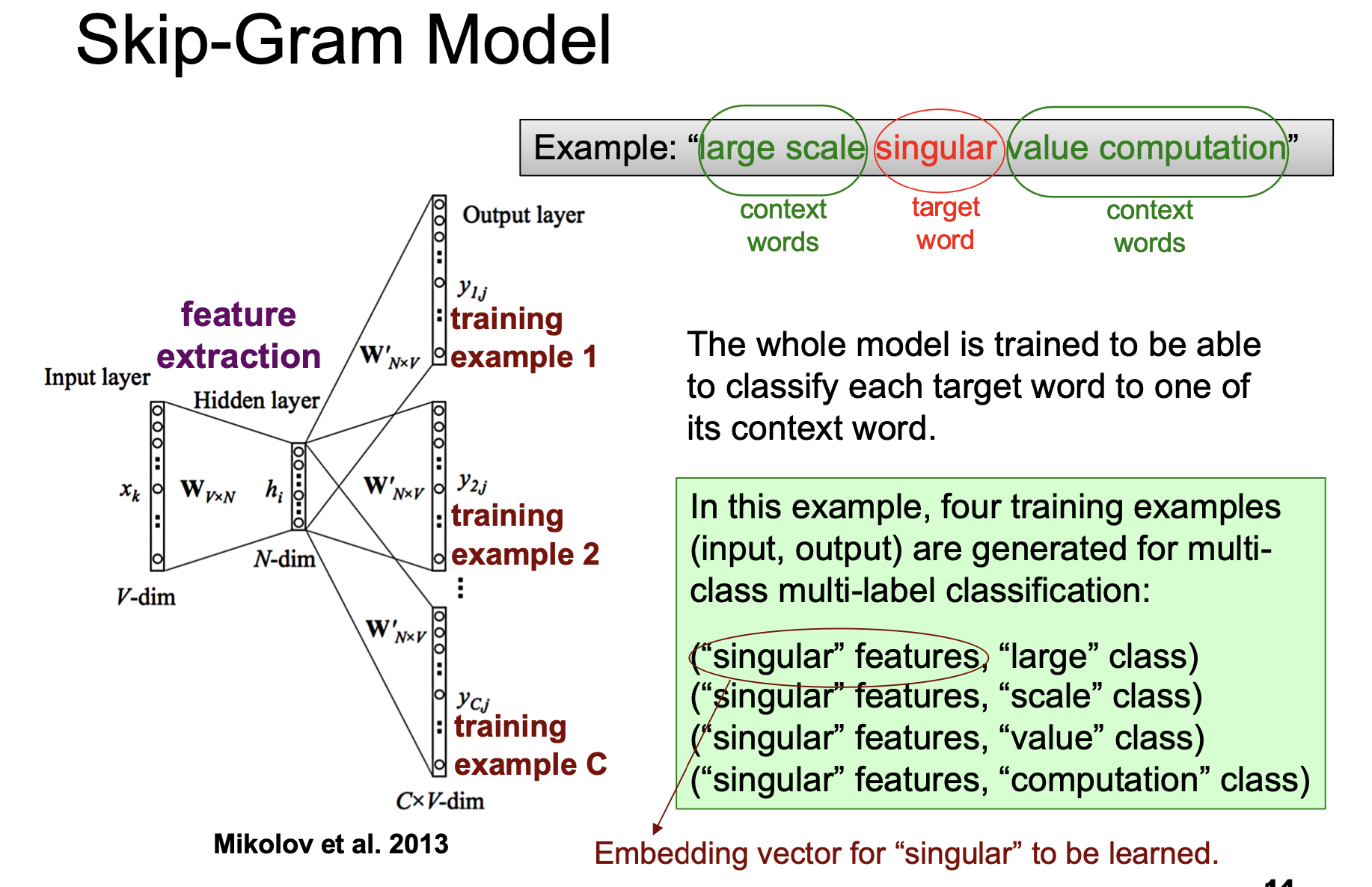
Skip-Gram 模型
Skip-Gram 模型的处理管线大致形态和连续词袋模型正好相反, 它需要解决的问题也大致恰好是反过来的: 给定目标词, 预测目标词的上下文.
GloVe 模型

