渲染方程 The Rendering Equation
从本章开始, 我们讨论支撑建模和动画的, 和实时且真实渲染相关的重要技术, 知识和概念.
渲染方程 The Rendering Equation
在此前的数节中, 我们介绍了多种通过 Shortcut 和近似等经验模型实现 类似现实世界中的光照效果 的方法. 下面我们讨论 基于物理世界的真实规则表达光照 的方法和技术.
为了准确表达光照所需要的物理量, 我们需要为光线在场景中的传播建立数学模型. 在现实中, 人之所以能观察到场景中的物体, 归根结底是因为 从一个或多个光源发出的光在经过和场景以及场景中的物体交互之后, 最终射入人眼并在视网膜上成像. 我们可以将这一过程抽象为下图所示的 渲染方程:
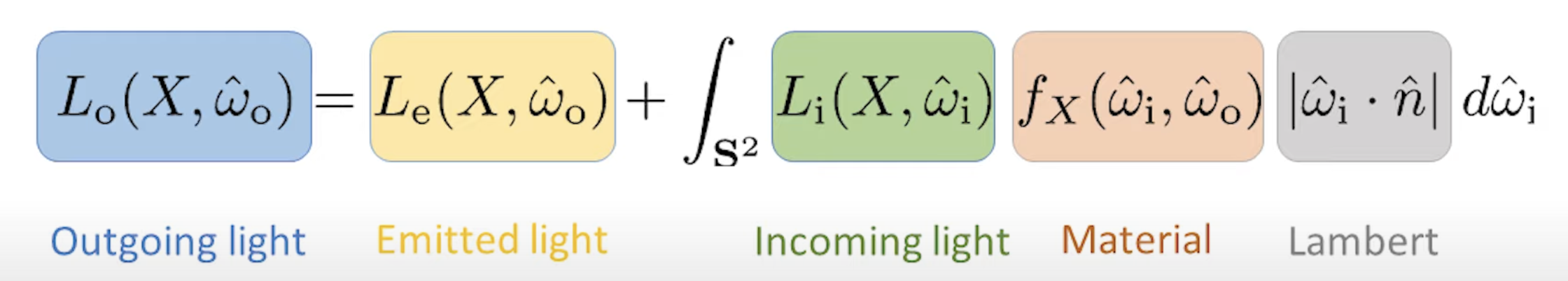
更详细地, 有:
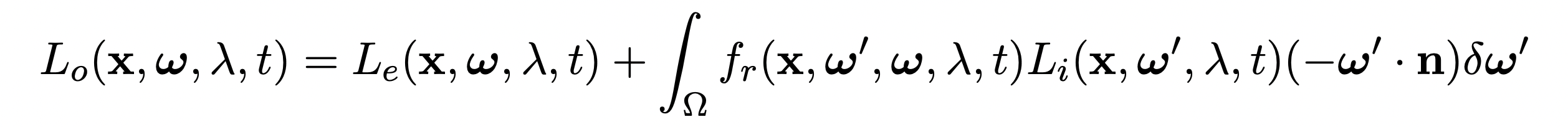
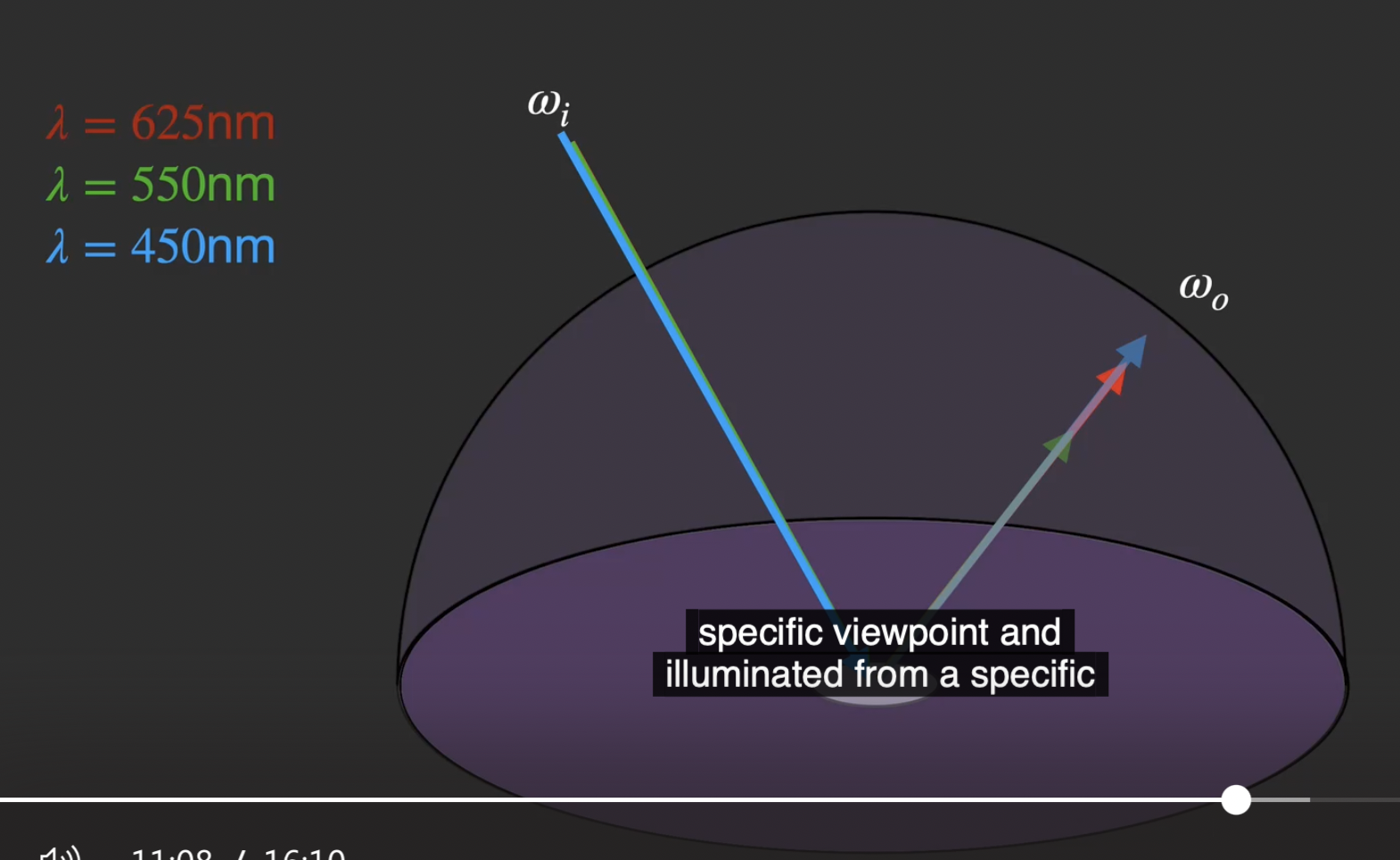
其中, $X$ 表示 场景中的某个位置, $\hat{\omega_0}$ (也就是第二个式子中的 $\omega$) 表示 从这个位置射到观察点的光的角度, $\hat{\omega_i}$ (也就是第二个式子中的 $\omega’$) 表示对于场景中的位置 $X$ 而言的入射光, 也是被积分项. 第一个式子就是第二个式子隐去关系不大的 时间 $t$ 和特定的光波长 $\lambda$ 后的简化版本.
可以看出, 本质上渲染方程的建模逻辑满足了 热力学第一定律: 在某个位置 $X$ 射出的光就是由 该位置 (上的物体) 本身发出的光 与 从所有可能的其他位置射到这个位置上的光 的 效果的组合. 由此渲染方程就被拆分为两项: 第一项描述该位置本身发出的光的效果, 第二项积分所描述的就是 “从所有可能的其他位置射到这里来的光” 的效果.
在积分项中, 该积分的实质是对 以该点为原心的一个半圆面上所有的点的光效 进行积分. 对于每个被积分的点, 积分中的项同时考虑了 射入到这个点的光效, 射入到这个点的光和该点的材质产生的效果 (也就是后面提到的 BRDF) 以及 由于入射角度不同所必需考虑的 Lambert Law.
同时, 渲染方程本身是线性的, 而且满足 Spatially Homogeneous 的性质: 这意味着它可以应用于 空间中的任何点, 无论它们的位置或者观察的方向如何.
我们还需注意到: 渲染方程实际上是 无限递归 (Infinitely Recursive) 的: 无论是从公式本身还是基于合情合理的分析, 如果严格按照渲染方程求解出场景中某处位置像观察点射入的光的颜色, 我们可能需要沿着光的路径一直分析, 而在分析过程中由于光可能会和多个物体交互多次, 因此为了计算一个渲染方程, 还需要连带着计算更多的渲染方程.
因此, 渲染方程作为一类 Fredholm Equation of the Second Kind, 我们 无法求出它的分析解. 我们实际上无法真正 “求解” 它, 而需要使用一系列技巧对其进行 近似.
光线与物体材质的交互: BRDF
我们下面讨论之前解释渲染方程时略过的部分: 描述物体本身材质对入射光影响的 BRDF.
当光射入物体表面时, 总的来说可能分别出现三种情形: 光在物体的表面被反射, 让物体的表面看上去类似 镜面 (Mirrored) 或 闪亮 (Shiny), 抑或 粗糙和平滑 (Diffuse), 取决于物体的表面是光滑还是粗糙.
第二种可能是: 光穿透物体表面, 并在物体内部发生反射和折射; 而第三种可能则是: 物体表面将入射光 吸收 或 部分吸收.
在实际情况中, 一般而言我们观察到的现象往往是上述三种不同情形的 混合. 而这些效果在渲染方程中则由建模物体表面光效性质的 BRDF 所描述.

我们首先考虑光在物体表面发生的反射.
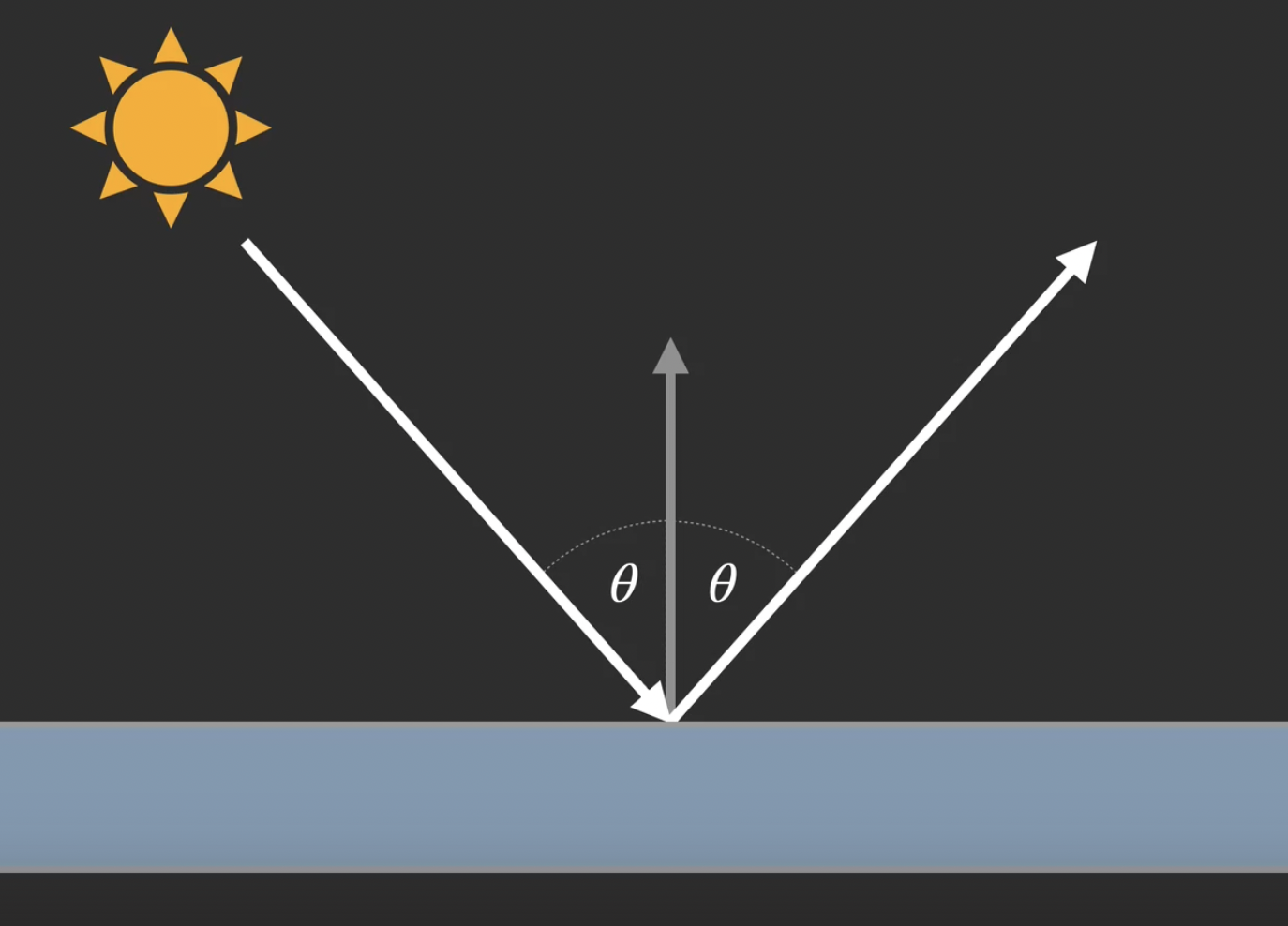
镜面反射 Specular Reflection
若光照到物体表面上之后向 唯一的方向 或 非常小的一个区域内的方向 (Narrow range of directions) 反射, 我们所观察到的将是 明亮, 镜面一般的物体表面 (Mirrored, Shiny Surface).
这也就是镜面反射的效果: 光以相同的角度从另一个方向射出, 让我们看到经过反射的画面, 感知到的, 画面的空间距离似乎就在镜面的对面一般. 具有镜面效果的表面一般都具有 金属质感, 这是由于在现实中使金属具有导电性质的自由电子具有 排斥电磁辐射 (如可见光) 的性质.
只要表面 平滑 (Smooth and Flat), 光就会在表面上发生 保持光的颜色 的 镜面反射, 在这种情况下画面的形状和主要的颜色都会被镜面反射所保留.
漫反射 Diffuse Reflection
若反射光向 多个方向漫无目的地发散, 则光照到物体表面上的时候所发生的反射就是 漫反射. 在现实中, 发生漫反射时往往 光略微穿透了物体表面, 如光打到看似平滑的纸上时实际上略微穿透了纸表面薄薄的一层 纸纤维, 由此导致光在物体内部发生了较为复杂的传播, 因此打乱了光反射的方向.

混合反射
另一种可能性时: 物体的表面并不完全平滑, 也不完全粗糙. 在这种情况下, 光打到物体表面发生的反射实际上介于纯粹的漫反射与绝对的镜面反射之间.
如果 总体来说, 光经过反射后的传播角度在一个 较小但并非小的离谱 的范围内时, 我们所观察到的现象就是 “较为浑浊的镜面反射”: 我们也许可以在物体表面观察到被反射的画面, 但画面的明亮程度可能远不如真正的镜面反射.
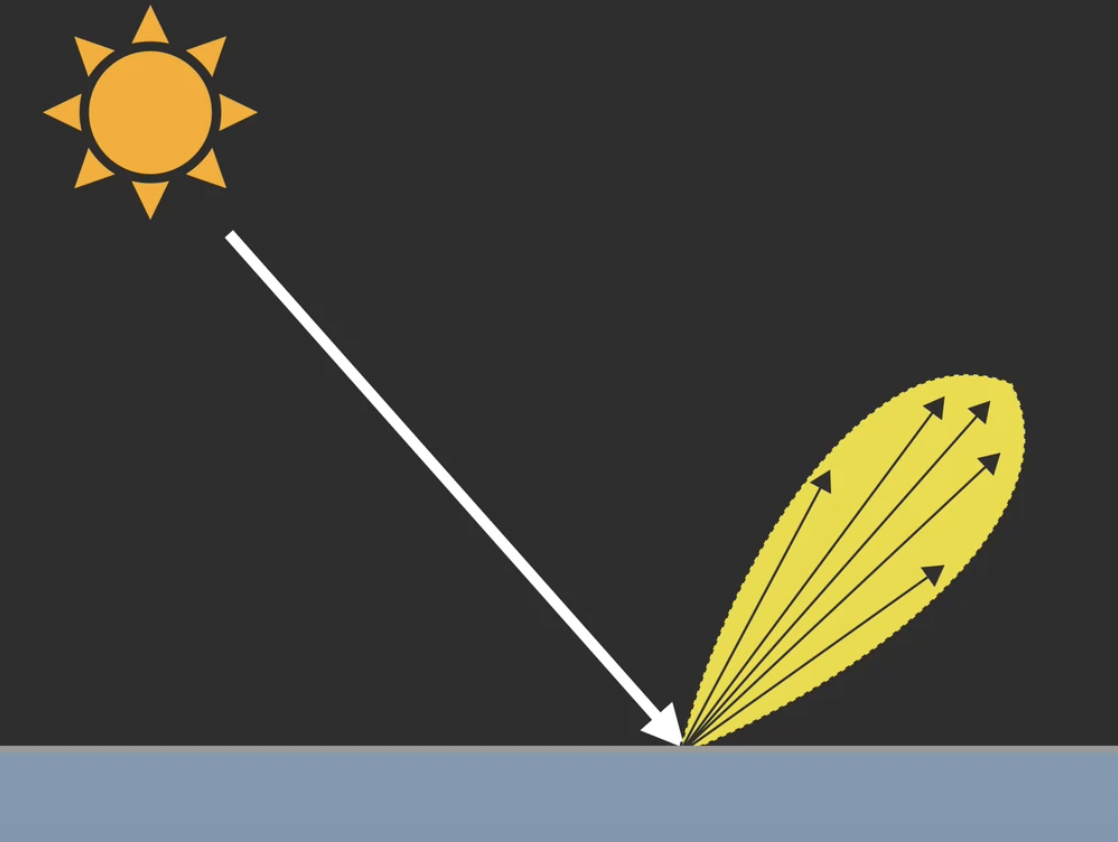
在现实中, 绝大多数的物体表面发生的反射都属于混合反射的范畴, 因为现实中 不存在绝对平滑的表面. 实际上, 即使在物体表面发生漫反射, 光也并非如理想状态的漫反射一般 均匀地向所有方向射出.
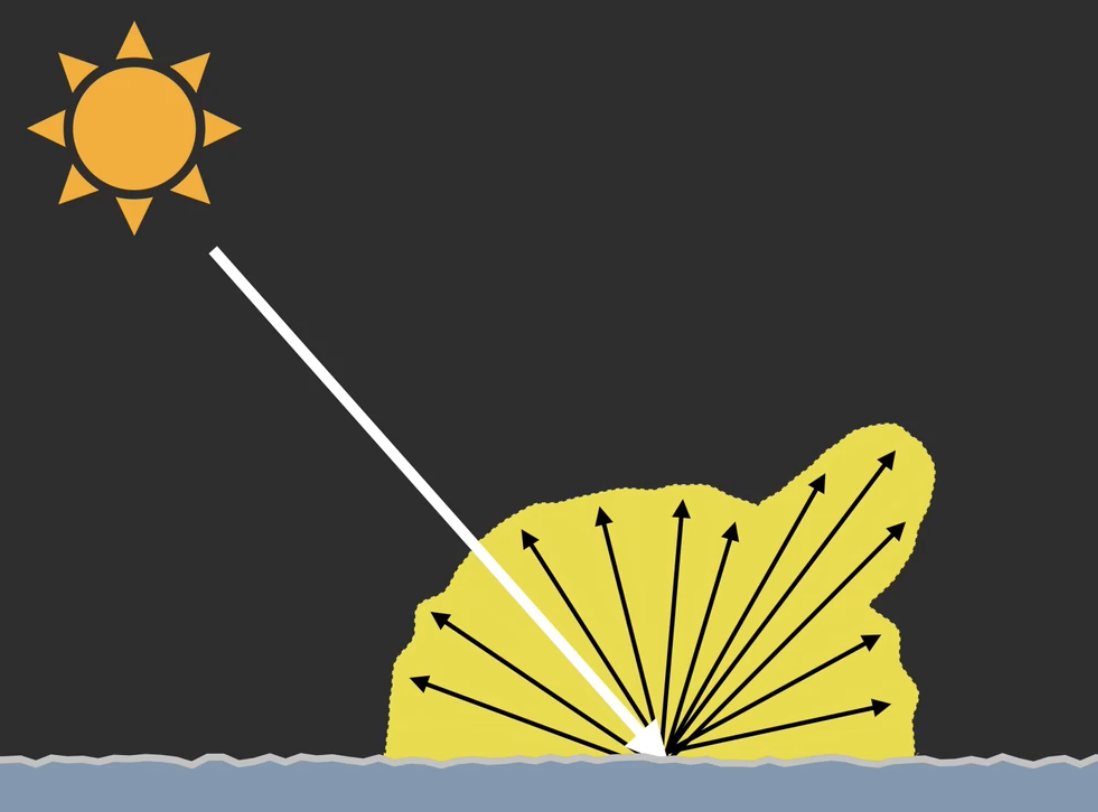
而 BRDF 尝试建模的就是这种复杂的现实情况. 总体上来说, BRDF 所描述的是 (在特定的时刻) 不同波长的光从特定角度射入物体的表面, 给定射出方向后, 射出的光强大小. 在详细解释 BRDF 前, 我们首先回顾可见光的定义以及肉眼对光的感知的性质.
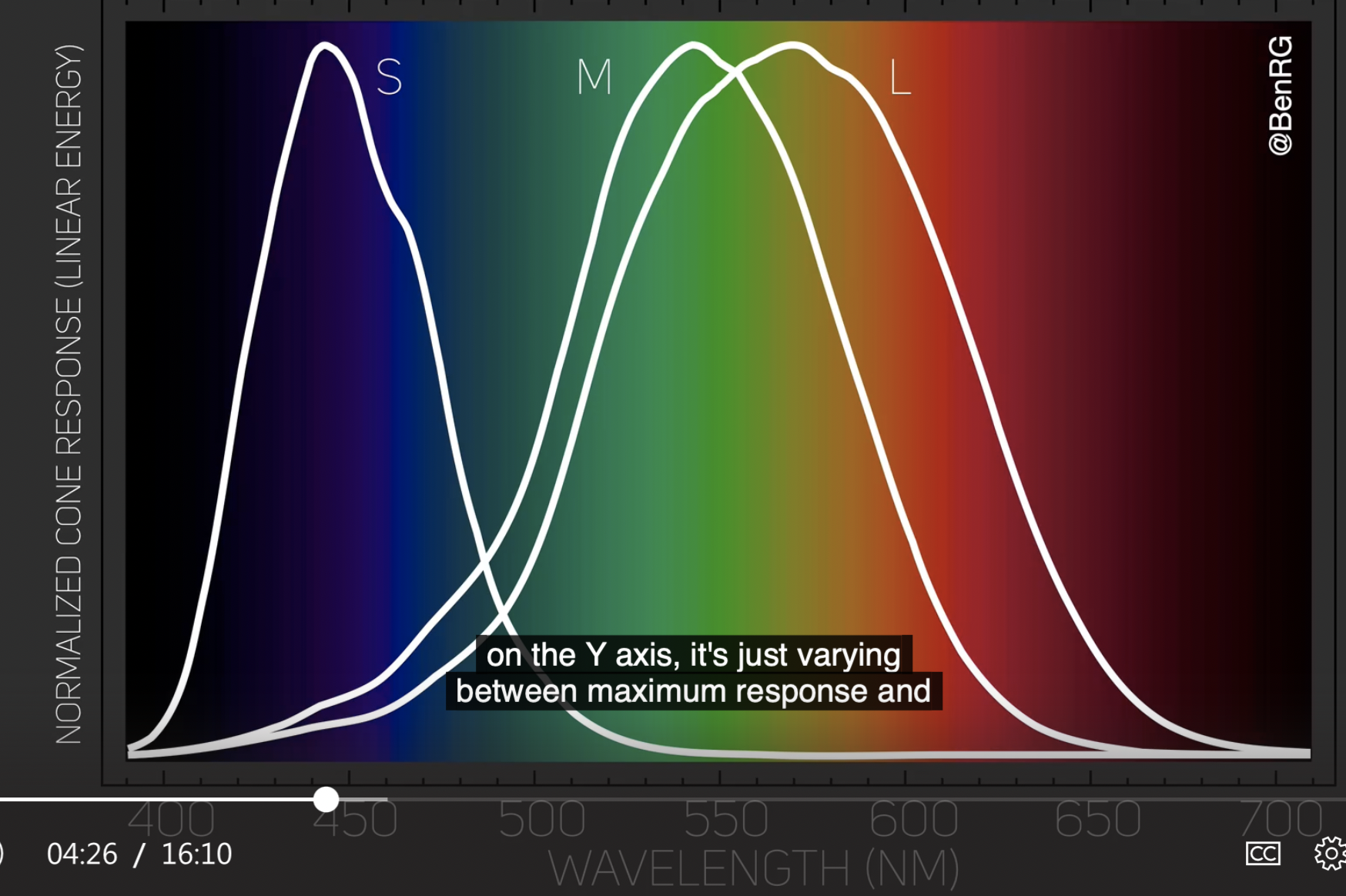
结合此前接触的知识, 我们知道视网膜上包含三种对不同波长敏感的视锥细胞. 它们在 可见光范围内, 实际上对范围内所有波长的光均敏感, 只是 不同视锥细胞的敏感度曲线不同, 如下图所示.
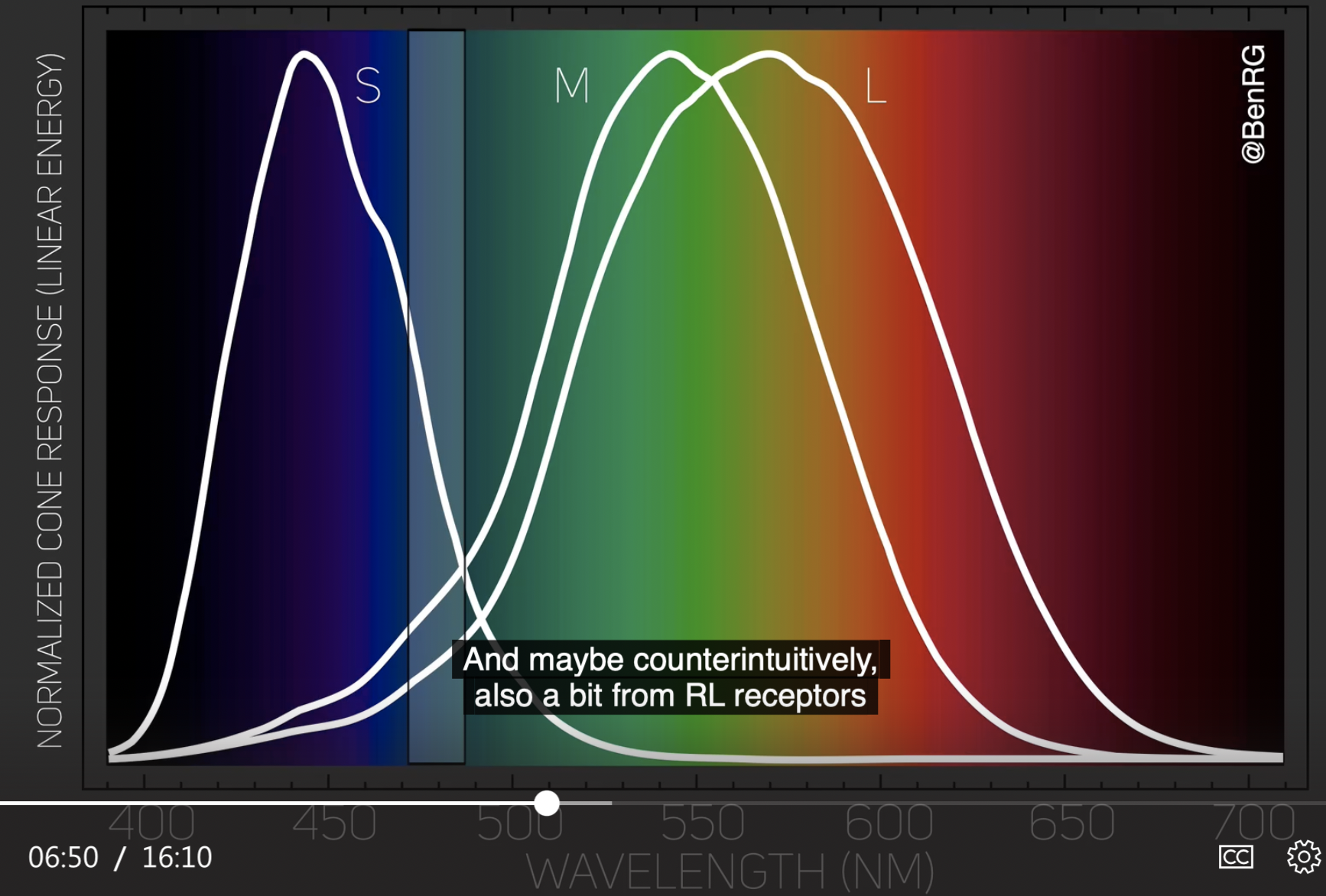
而实际上, 我们所观察到的光的颜色不完全取决于 这束光本身的波长, 本质上是取决于 这束光对视网膜上三种不同视锥细胞的刺激程度的总和: 如下图所示的这片区域内的 “蓝紫色光”: 我们既可以向视网膜发射 纯的蓝紫色光, 也可以通过适当的调制使 视网膜上三种不同视锥细胞接受的刺激程度总和与接受纯的蓝紫色光的刺激程度总和相同, 这样 即便射入视网膜的是本质上完全不同的两类光, 视网膜向大脑传达的信号 也是完全一致的, 在感知上, 我们所感受到的光的颜色 就是完全一致的, 这也就是可以使用 三原色 经过合适的混合 “产生不同颜色” 的原因: 我们实际上所产生的并非是 “真实的彩色”, 而是 “与真实彩色对视网膜的刺激相同的混合颜色”.
下面继续讨论 BRDF. BRDF 可以在概念上被简化为下图所示的 “辐射比例公式”: 给定光的入射角和出射角, BRDF 的值可以视为 反射出该点的辐射与射入该点的辐射 的比值, 表现为 光的能量损耗.

而 BRDF 的详细公式所建模的就是: 在球面坐标系上, 若某一束光以特定的入射角和方位角 (Azimuth) 射入点 $X$, 在这个球面的特定位置 (同样由一组方位角和偏角所确定) 观测到的光的 光强.
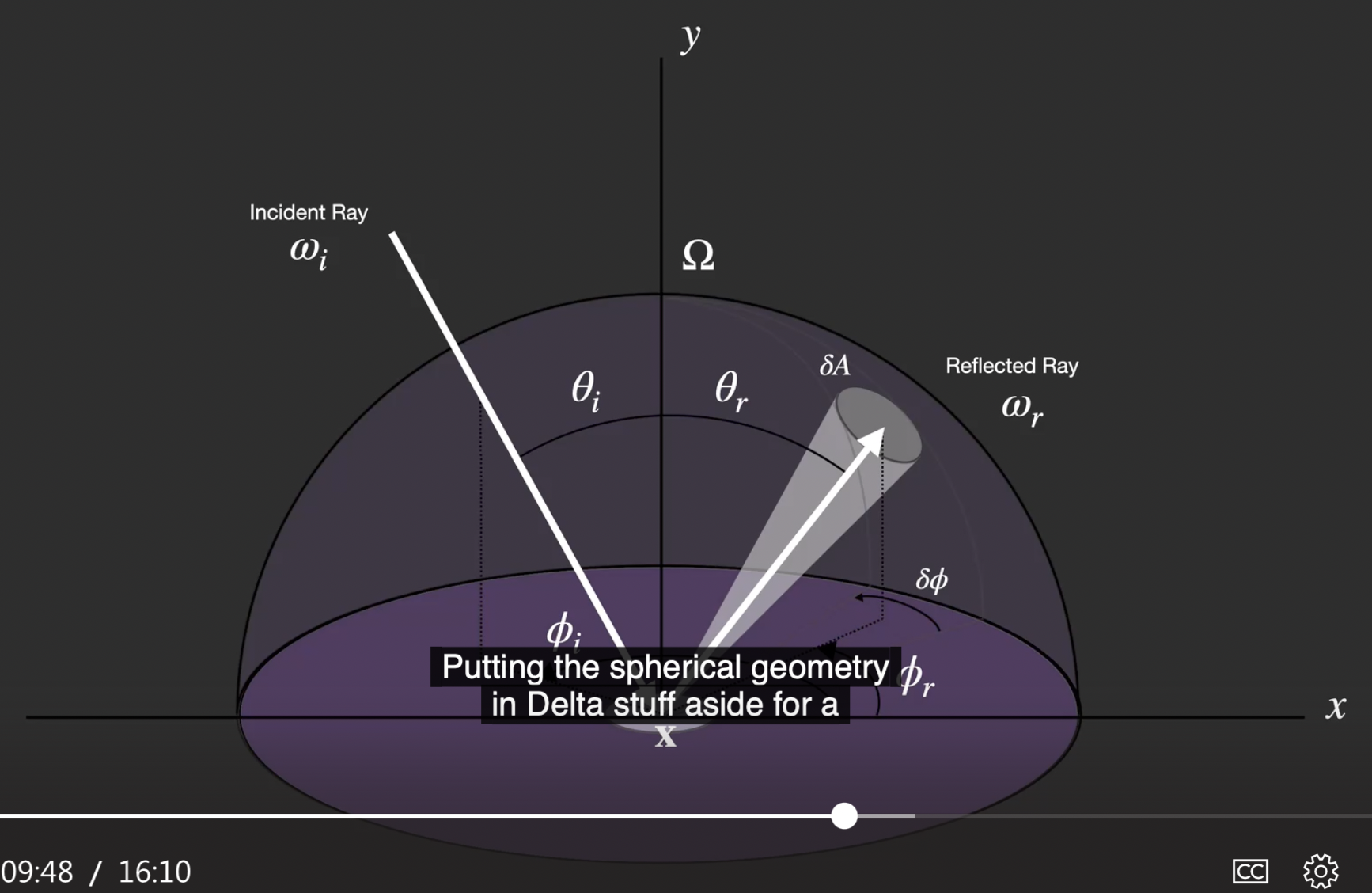
因此为了便于理解, 我们可以将 BRDF 简化为:
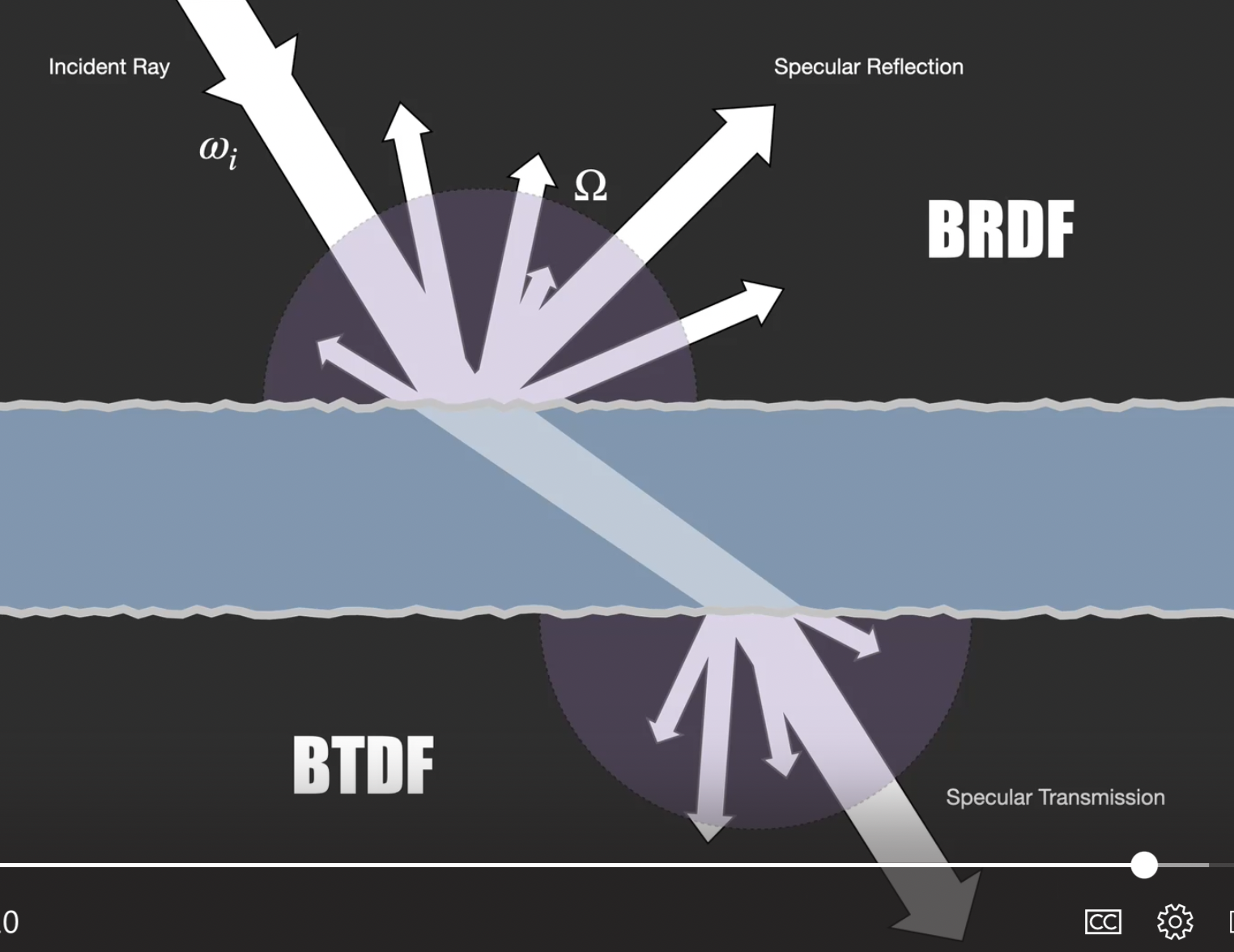
BRDF 唯一 地建模了物体表面关于不同波长的光的交互性质, 因此不存在所谓的 “the BRDF”. 在历史上, 对物体表面关于不同波长的光的反射/吸收/交互性质的测量是 手动进行 的, 如下图所示.

如果将物体表面对 特定波长 的光的交互性质可视化, 我们得到的大概是这样的图像:

其中这些奇怪的三维模型在不同角度上的长度 (大小?) 表示的就是物体表面在这个角度对特定波长的入射光的能量削减程度.
最后, 需要注意 BRDF 仅仅是对 物体表面反射光效果 的建模. 对于 透射 (Transmission) 的建模, 有对应的 BTDF (虽然它的实质和 BRDF 别无二致, 只不过一个建模的是反射光, 一个建模的是透射光):
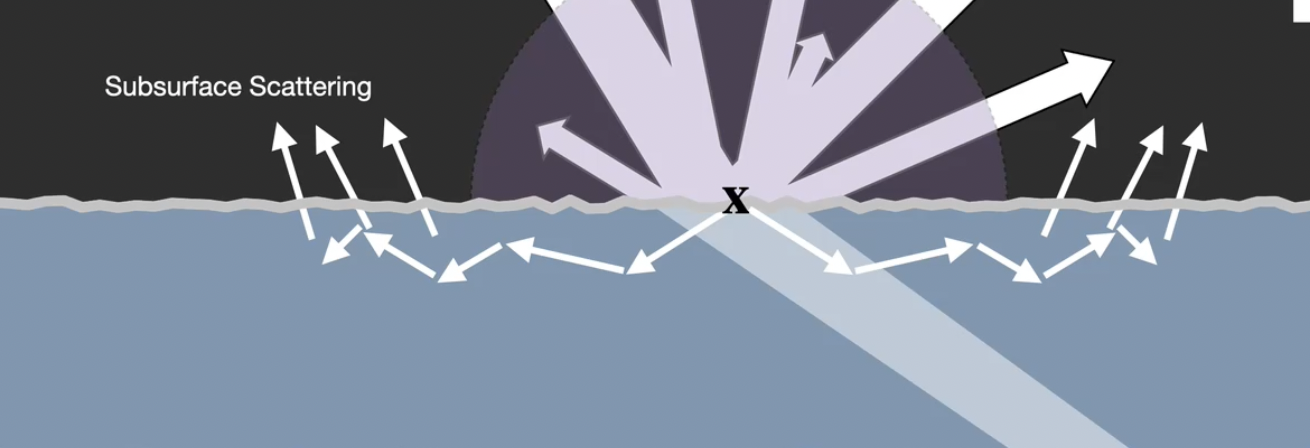
更复杂地, 对于 光射入物体表面后, 稍稍穿透物体表面并在物体接近表面的内层发生反射并最终射出 的 Subsurface Scattering (次表面散射), 也有对应的 BSSSDF 对其专门建模.
最后, 我们常常将同时建模了 反射, 透射 和 次表面散射 的量称为 BSDF.

