复杂粒子模拟和物体碰撞
下面我们讨论一些基本的 模拟方法.
上一章中我们介绍了 大规模弹簧模拟 (Massive Spring Simulation) 和 粒子模拟 (Particle Simulation), 这些模拟的基本单位都是 质点. 我们下面讨论以 几何体 (Geometry) 为模拟对象的另一种模拟方法: 刚体模拟.
刚体模拟 Rigid Body Simulation
刚体模拟的最基本兑现是 几何体, 它和质点的第一个区别在于: 对于质点我们不考虑 坐标轴上的旋转, 而对几何体而言, 由于它具有 形状, 因此必须考虑它的旋转, 因此几何体具有 $6$ 个自由度: 三个分别在 $x, y, z$ 轴上的 位移自由度 和关于三个坐标轴的 旋转自由度.

增加的自由度使刚体模拟更加复杂, 而 如何处理刚体和环境中其他物体的交互 则是另一个困难点. 以 碰撞 为例, 刚体和其他物体之间发生碰撞时, 刚体本身或被 回弹, 或会围绕某个点 旋转,
因此, 在考虑刚体和其他物体的碰撞时, 不同于质点碰撞中只需考虑影响物体位移的 反弹力, 还需考虑改变刚体旋转状态的 扭转力 (Torque).
模拟刚体碰撞的一个常用办法是 冲量法 (Impulse-based collision), 它直接计算碰撞对物体 速度的改变情况, 而非一步步地先计算受力, 然后计算加速度, 最后根据时间推移依次算出物体运动状态的改变情况.
冲量法不仅适用于刚体碰撞的模拟, 它同样可以模拟大规模弹簧系统中每个质点的运动情况.
同样, 当刚体和别的物体 静止接触 时, 就需要 忽略在这种情况下模拟方法带来的噪声可能对物体速度产生的改变. 自然, 当物体相互接触而非碰撞时, 我们希望它们保持当前的静止状态不变, 比如把石头放在桌子上, 自然石头就不该自己动起来. 而如果不忽略模拟方法的噪声, 我们所模拟的石头就可能会不断的振动, 因为此时计算的速度改变量虽然极小, 但不为 $0$. 这一原则称为 Rest in contact: 当两个物体静止地相互接触时, 直接 停止对它进行刚体模拟, 由此避免产生微小的速度改变量.
刚体之间的交互除了碰撞之外还有 堆叠 (Stacking). 如下图所示, 多个刚体之间上下堆叠, 由于受力平衡此时所有物体均相对静止.

绞接刚体 (Articulated Rigid Body)
下面考虑对 绞接刚体 的模拟. 上一章介绍的 骨架装配 环节中就会涉及绞接刚体的模拟: 假设骨架中的骨头就是刚体, 连接骨头的关节就是对刚体的 铰接.
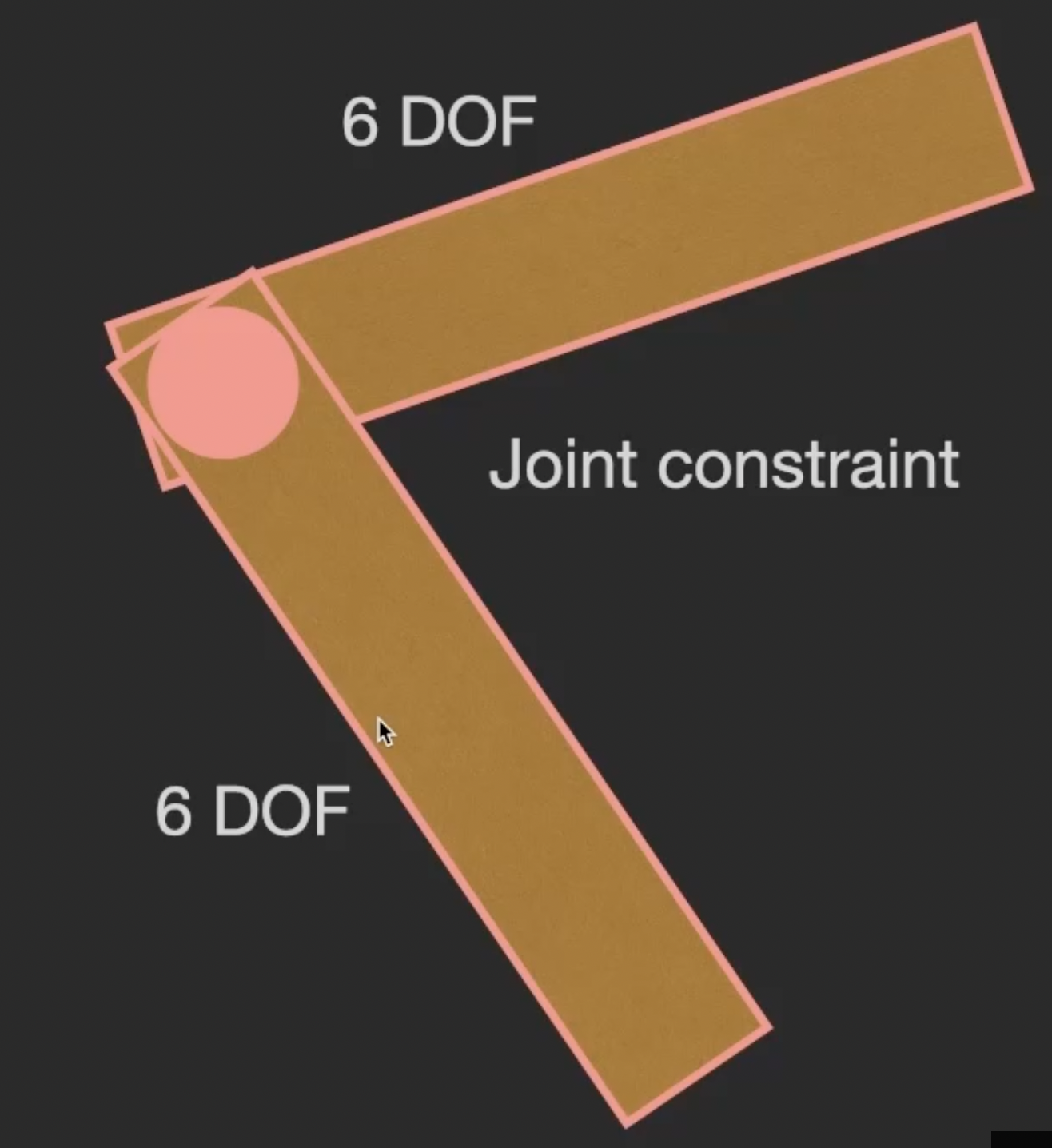
下面考虑将两根骨头用一个关节铰接在一起. 此时我们称关节为 关节约束 (Joint Constraint), 因为显然在引入铰接关节后, 原来的两根骨头都 失去了一些自由度, 无法像以前一样随意运动.
下面是对自由度的分析: 上面已知, 任何刚体的自由度都是 $6$, 因此在不考虑关节的情况下, 两个骨头 (刚体) 共有 $6 + 6 = 12$ 个自由度.
此时引入铰接关节. 显然可见, 铰接关节的引入约束了刚体的两个 旋转自由度: 它只允许刚体基于关节转动. 同时, 铰接关节将两个刚体 合二为一, 故此时它们构成了一个 组, 在这个组中的全体元素 共享位移自由度, 因此可知铰接关节还约束了刚体的三个 位移自由度, 所以总体上铰接关节的引入约束了五个自由度.
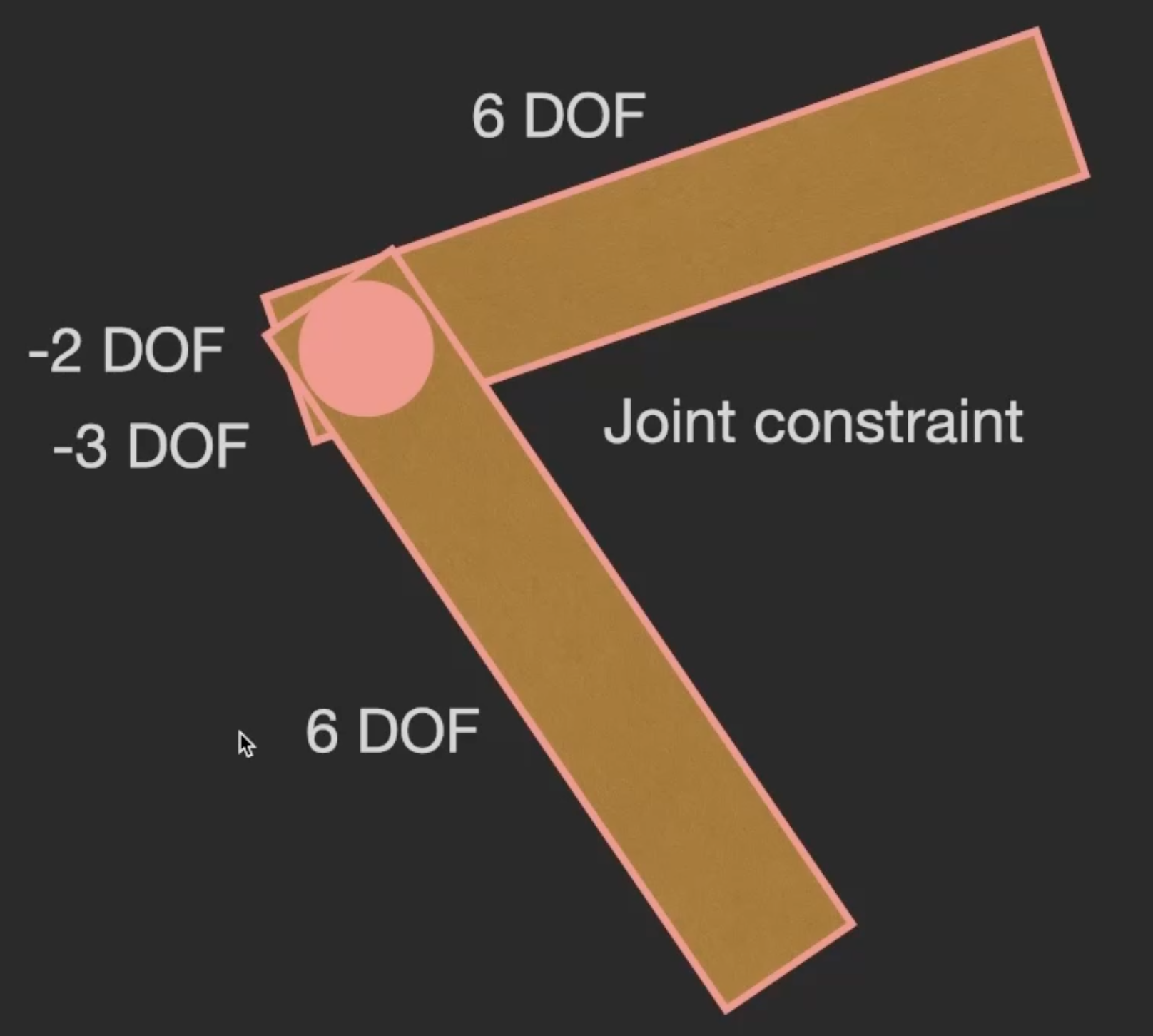
绞接刚体可用于包括但不限于 车辆, 骨架 等任何 包含了互相连接的刚体 的物体. 我们可以使用绞接刚体建模法, 基于刚体之间连接类型的不同, 计算出刚体的可能运动自由度.
可形变物体 (Deformable Objects) 的模拟
下面考虑 可形变 物体的模拟. 由于此时物体本身具有 可塑性 和 弹性, 刚体模拟中的规则不再使用.
有限元方法
有限元方法 (Finite Element Method) 是其中一种最常见的可形变物体模拟方法. 其基本逻辑是将物体 分解为多个四面体, 这个过程也称为 四面体化 (Tetrahedralization).
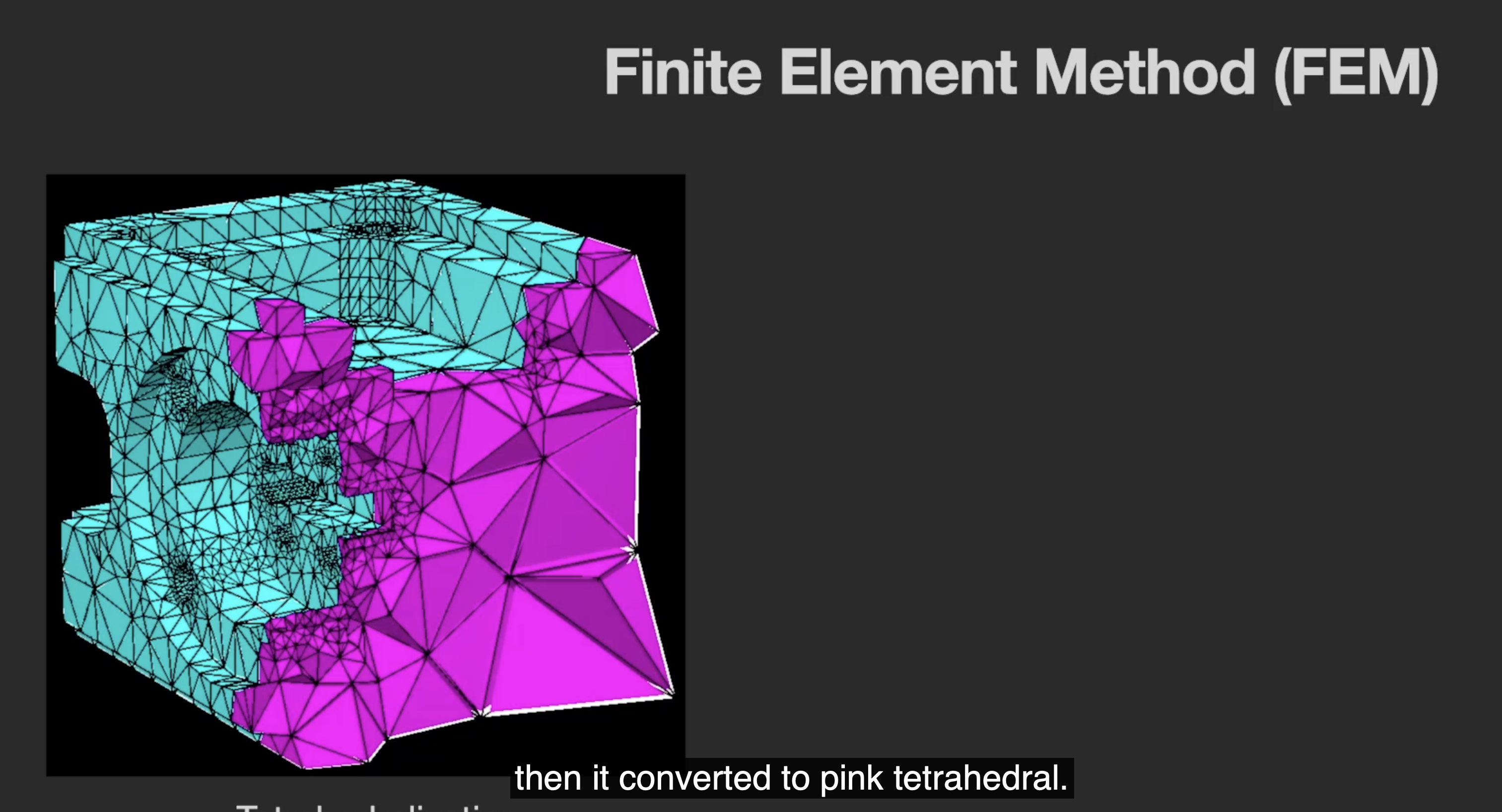
如上图所示, 有限元法将蓝色的物体转换为红色的, 由多个四面体组成的新形式. 此处将转换的目标设为四面体的主要原因是: 四面体是最简单的, 具有体积的三维物体.
随后, 对组成物体的每个四面体, 都逐个定义它的 Rest shape 和 Deformed shape, 假定四面体总是倾向于 回归到 Rest Shape. 因此和大规模弹簧模拟类似, 通过定义组成物体的每个四面体的形变规则, 就可以计算出 将物体从当前状态形变到另一状态, 所需施加的力的大小和方向.
布料模拟和破碎模拟
大规模弹簧系统 可用于模拟 布料 和 物体破碎. 前者的基本原理已经在上一章中解释, 下面讨论物体破碎模拟.
使用大规模弹簧系统模拟物体碰撞并碎裂的情况, 只需将 “连接质点之间的弹簧” 的 脆弱程度 Stiffness 适当提升, 使弹簧受到超过一定阈值的力后 破裂断开, 所受到的力再 传导到相邻质点上, 由此就可以模拟物体碰撞后碎裂的情况.

流体模拟
在上一章中我们还介绍了 使用粒子模拟法模拟流体 的思想. 常用的流体模拟方法是 Lagrangian Fluid Simulation, 本课程只提及术语, 不进行系统的介绍.
在实际渲染时, 我们会将相邻的几个质点转换成 网格 (Mesh), 也就是将它转换为平面, 然后使用诸如法线等平面表示 (Surface Representation) 结合纹理贴图进行相应的计算.
另一种流体模拟方法称为 基于网格的流体模拟法 (Grid Based), 其基本思路是:
-
将流体用网格切分为一个个的 块, 每一个块都是这部分流体的 限位框 (
Bounding Box). 这一步称为 分立化 (Discretization).
-
然后就需要分别对分立化后得到的每个
Voxel(也就是体积块, 在后面讨论体积渲染-直接体积渲染时会再次提及) 的属性进行分析, 确保 在运动过程中, 对每个Voxel, 流入的流体体积和流出的一定相等. 求解网格流体模拟的通用方法为Eulerian Fluid Simulation. 同样, 在此处不详细介绍.
进一步地, 结合网格模拟的 Eulerian Fluid Simulation 和粒子模拟的 Lagrangian Fluid Simulation, 就得到了 混合流体模拟法 (Hybrid Fluid Simulation). 它具备二者的优点, 在模拟中同时考虑了网格和质点粒子, 可用于模拟布料, 烟雾等.

碰撞检测
下面讨论 碰撞检测, 它主要回答的问题是: 在建模的空间中, 哪些物体 在 什么时间 以 什么样的方式 发生碰撞.
碰撞检测问题的难度一方面取决于发生碰撞的物体的碰撞表面类型是什么. 如果发生碰撞的物体表面都可用 曲面的隐式表示 描述, 则判断两物体是否相撞则是一个非常简单的问题, 而对于其他的曲面表示, 比如 网格表示 等, 要判断物体之间是否发生了碰撞就相当困难了.
我们同时需要计算 何时与何处发生了碰撞. 一般地, 算法检测到碰撞时, 在建模的空间中物体的碰撞其实 已经发生, 因此可以利用这一现象使用 回溯法 (Backtracking) 计算碰撞发生的时间和地点: 考虑未来某个时间点上物体的状态, 若发现物体已经相撞, 则反过来推算物体何时恰好相撞. 这一技术常用于对光线路径的计算.
另一种取巧的方法称为 Quick Dirty Fixing, 其基本逻辑是: 取一个 “两物体已经发生碰撞” 的时间点, 并且认为物体碰撞后无事发生, 两个物体 “互相对穿”. 然后, 将一个物体的当前位置投影回另一个物体表面, 把这个投影得到的位置近似地视为这两个物体发生碰撞的位置.
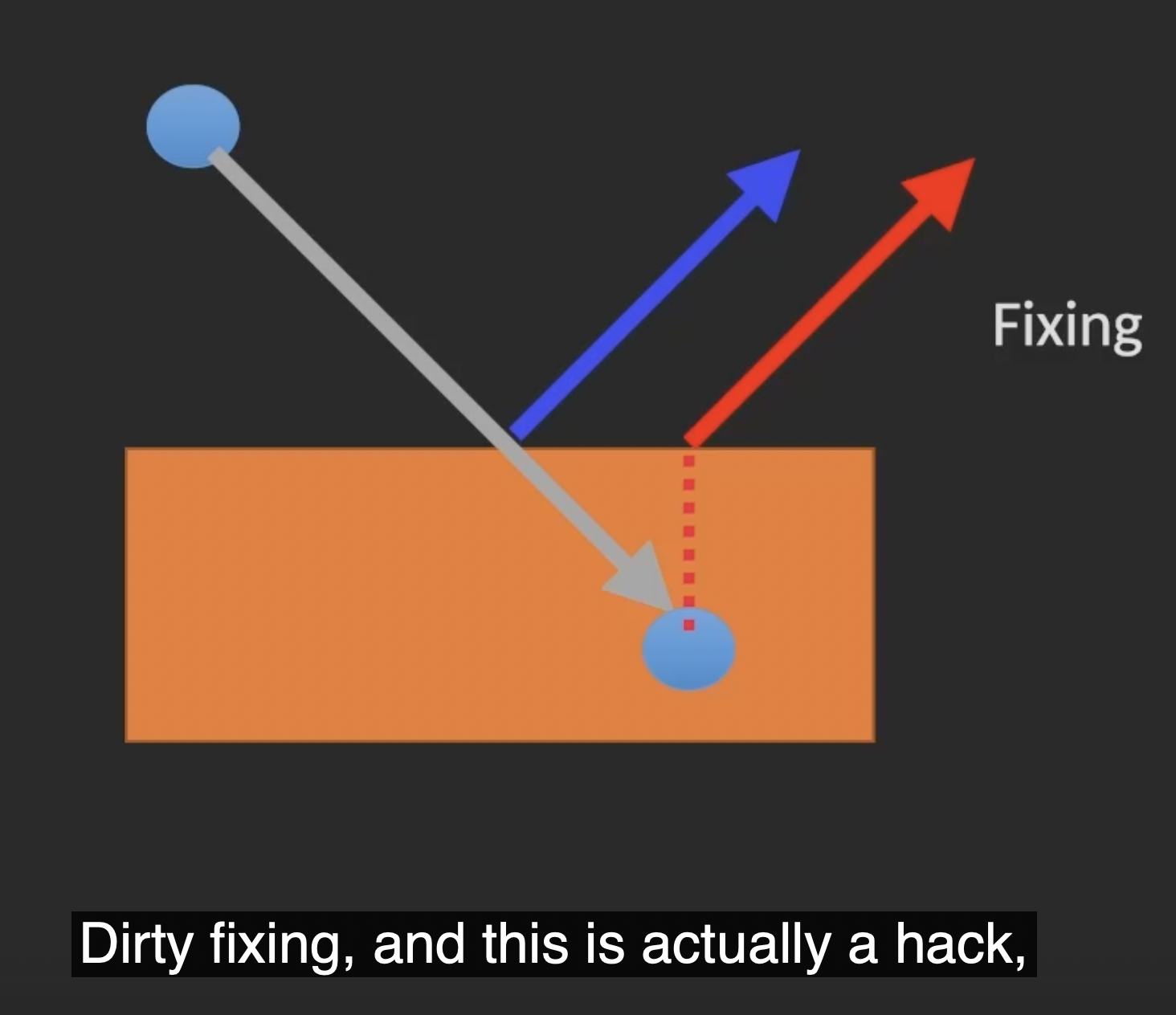
这一方法很不精确, 但计算速度很快. 如果要考虑 $N$ 个物体之间的相互碰撞, 执行碰撞检测的次数就是 $O(N^ 2)$, 因此快速计算物体碰撞的反馈还是很重要的.
减少计算量的方法包括 减少检测次数, 如将空间中的物体进行逻辑分划, 不去考虑显然不会发生碰撞的物体, 以及 进一步简化物体的碰撞逻辑, 如使用 碰撞箱 (Collision Box) 代替物体本身, 如果物体的碰撞箱不重叠显然它们不可能碰撞, 就无须再执行更精确的碰撞检测.
基于对碰撞时物体 边缘体积 (Bounding Volume) 的选择, 衍生出了多种碰撞检测算法:
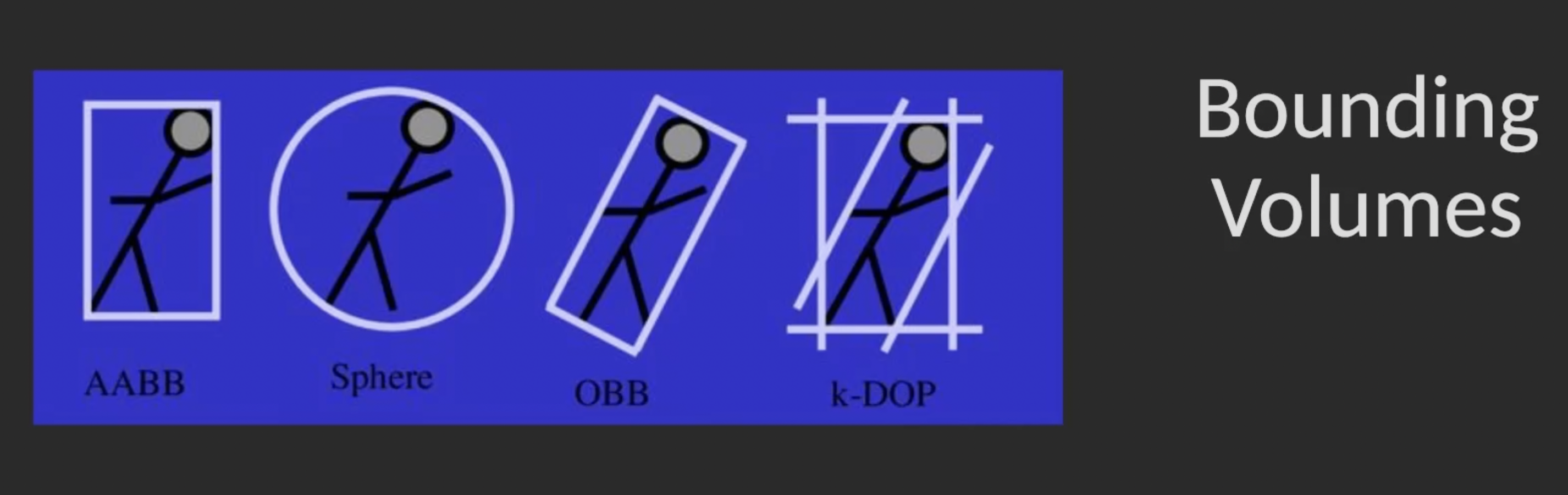
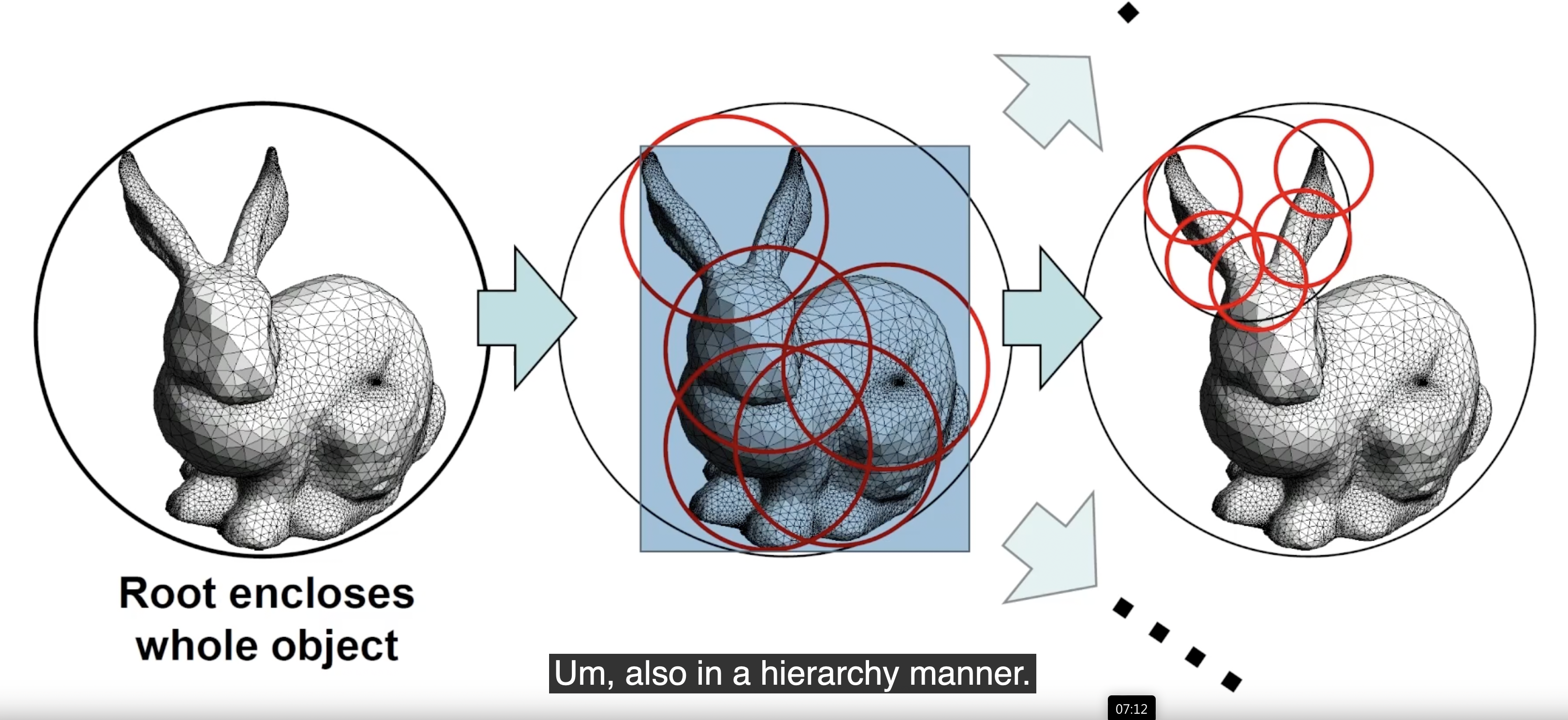
如 AABB: Axis-Align Bounding Box, OBB: Oriented Bounding Box 和 k-DOP: k-Discrete Oriented Polytope. 下面考虑最简单的 Sphere: 它将一个 恰好可以包住物体的圆/球 作为物体的碰撞检测边缘.
无论物体的碰撞检测边缘是什么形态的, 只要两个物体的检测边缘 不相交, 就可认为它们之间不发生碰撞. 在具体实现中, 由于物体本身也可以分为多个组成部分, 因此物体的碰撞检测边缘也可以基于同样的 逻辑层级 构造: (实际上也就是后面介绍的 “Hierarchical Bounding Volume”)