分词, 语言模型和语言表示
本章将讨论分词问题, 介绍数种主流的语言模型并讨论语言表示问题.
1. 分词
分词 (Tokenisation) 是文本数据进入到模型进行计算前必须经过的步骤, 其主要目标是将文字输入 拆分为最基本的组成元素: 字词 (Tokens).
最简单的分词策略是将文本数据 基于空格或其他标点符号 进行拆分, 但这样的方法一般情况下都是不准确的. 分词策略的选择和构造取决于 被拆分的文本数据所属的语言类型 和 文本数据本身所包含的内容主题.
举例而言: 中文 不使用空格分离字词, 而日文数据中一句话里可能夹杂平假名, 片假名, 汉字和罗马字符; 以阿拉伯语和希伯来语为代表的一些语言遵循 自右向左 的阅读顺序, 但阿拉伯数字的阅读顺序却又始终是 自左向右.


同时, 一些 具有特殊含义的词 往往包含连接号 - 或空格 ` `, 此时若使用最基本的分词策略就会出现明显的问题.

此外, 如何进行分词在一些情况下还是 主观的, 并无明确的标准. 如下图的例子所示, 若要对 900g/21lb 进行分词, 就可能出现多种不同的分法, 而这数种不同的分法都有一定的合理性.

因此, 分词在实际应用中是一个非常复杂的问题. 一般地, 分词包含下列的四个步骤:

下面以英文为例简要解释这四个步骤.
1.1 初始分词
在英语中, 绝大多数的字词都被 空格和标点符号 (Word and Punctuation) 所 划分和界定 (delimit). 因此, 可通过下列的两个步骤划分出 字词的粗略边界:

这一步可以生成相对不错的单词划分, 但它可能存在 过分割 Over-Segmentation 和 欠分割 Under-Segmentation 问题:

因此我们需要执行后续的三个步骤以对初始分划的结果进行 细化或修正.
1.2 处理缩写和省略撇号
第二步的主要工作是:
-
处理 缩写 (
Abbreviation) 导致的潜在分划错误:一般地, 在 缩写 的内部出现的句号 (
period) 应该被认为 属于该缩写的一部分, 因此需要和这个缩写一起被划分为 一个单独的字词.
一般地, 连接在单词末尾的句号表示 该句子的末尾, 因此需要被划分为一个单独的字词. 但若某个句子的结尾是一个缩写词, 此时末尾的句号就同时包含了 表示缩写 和 表示句子结尾 的双重含义. 在处理一些特定语料时, 可能需要 强行将这个句号从缩写字词中拆分 或 强行将这个句号包含到缩写字词中, 因此需要这一步检查.
此外, 包括 逗号 (
Comma), 分号 (semi-column), 引号 (quotation mark) 等标点符号都应该被视为 单独的字词. -
处理省略引号因歧义性导致的潜在分划错误:
引号存在 歧义性, 因其根据语境不同可以解释为 引用标记 (
Quotation Marks), 所属格符号 (Genitive Marker) 和 后附着语素/重读词后词 (Enclitic):

1.3 处理连接号
连接号的含义也存在 歧义性: 它可能在被分行的文本材料中表示句子在上下两行之间的连接, 也可能是某个 合成词 (Compound Word) 中不可分割的一部分. 因此我们需要对分词结果进行进一步检测以修正由于连接号的歧义性所导致的潜在分划错误.


1.4 处理其他难以归类的特殊表示
最后, 我们需要处理文本数据中可能存在的, 难以归类的特殊表示, 如下图所示:

需要处理哪些特殊表示, 数字和日期等特殊表示应该如何分划, 都需要基于具体的文本数据而定.
1.5 对分词和相关问题的总结与讨论
最后总结: 在分词这一步中, 实际上 不存在唯一正确的规则, 任何与对应的自然语言处理系统 一致 的分词规则就是理论上合适的规则.
需要注意: 分词遵从的 基本原则 是: 从完全未被划分的初始语料出发, 基于 一系列规定好的划分规则 将语料一步步地划分, 从而 避免过划分的问题出现.
分词是 文本预处理 (Text pre-processing) 的重要一步. 文本预处理还包括 文本文件级别的预处理 和 词汇级别的预处理, 分词是承上启下的一步.
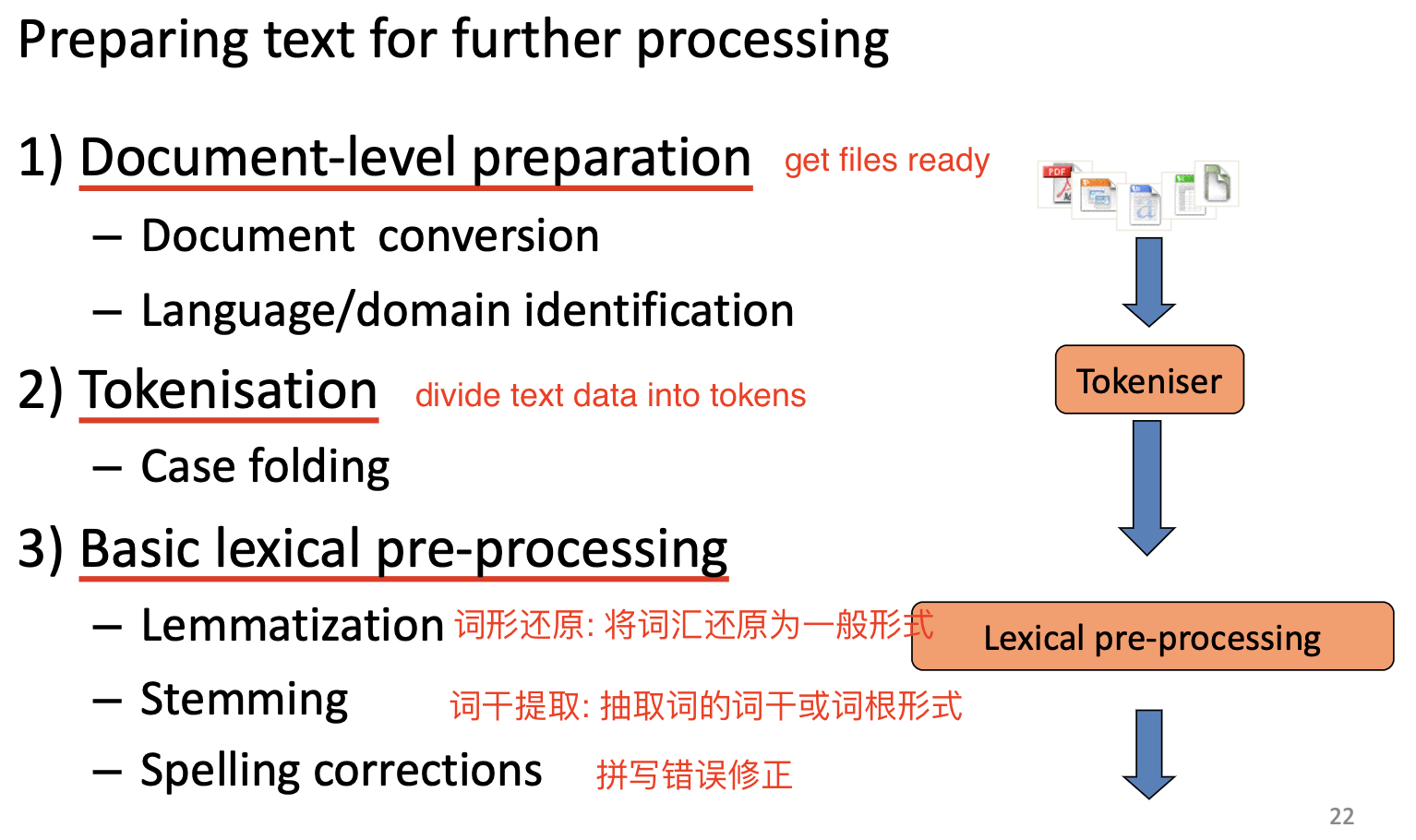
此外, 大小写折叠 (Case Folding) 也是一个受 歧义性困扰 的问题. 由于有大量的 著名名词 (Popular Noun) 是由首字母大写的普通名词拼合而成的, 因此如果将所有单词全部转成小写就会导致信息丢失.

一种方法是: 仅将句子开头的首字母改为小写形式. 这也被称为 truecasing. 更合适的解决方案还是基于机器学习构造自动大小写折叠模型.

2. 语言模型和语言表示
我们接下来介绍数种主流的语言模型和语言表示.
考虑一个最简单的语言相关问题: 完形填空. 从未接触过文章中所描述内容的学生也能正确填出留空的单词, 其背后是基于 足够多的语料阅读 所积累的 语感. 相应地, 比起完全形式化的, 基于 语法 所构造的复杂语言模型, 我们基于从现实中收集的大量语料数据为语言进行 统计学意义上的建模. 我们用 概率数值 表示给定语料 可能在现实中出现 的概率, 自然而然, 更 符合人类理解常规, 运用更自然 的语料被分配的概率值就更大.
形式上说, 所谓的 语言模型 (Language Model) 就是这样一个以 任意语料 为输入, 以某个解释为 概率 的, 位于 $0$ 到 $1$ 之间的数值为输出的 函数.

所谓 模型, 就是对某个现实事物的 抽象, 简化 的表述. 对 语言模型 而言, 自然就存在这个问题: 应该如何表示语料数据?
2.1 词袋表示 (BoW Representation)
词袋表示 (BoW Representation) 是最简单的语言表示方法, 它将含有顺序和符号的语料简化为一系列字词, 将其装进 包含重复元素的集合: “词袋” (Bag of words) 中.
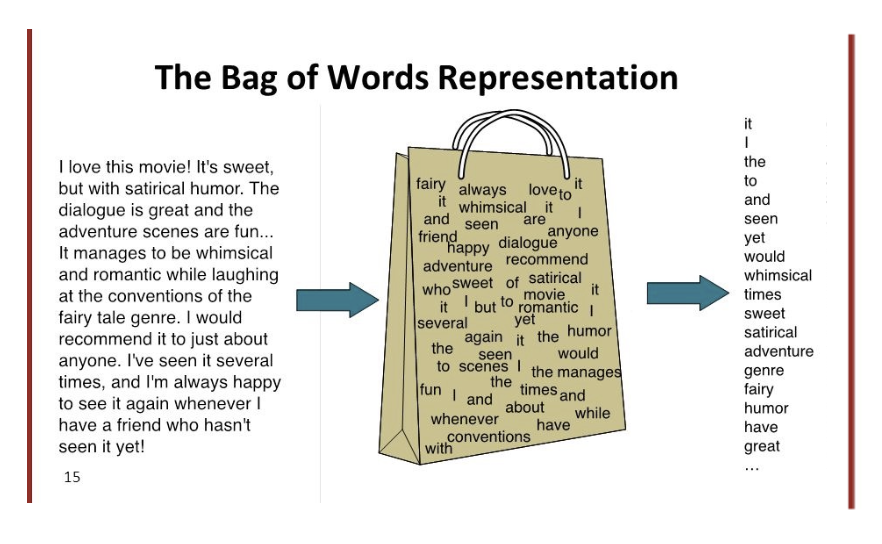
词袋模型非常简单, 以至于语料在转换为词袋表示的过程中会不可避免地损失信息, 如 单词之间的顺序会完全丢失, 转换后无法区分单词的相对重要性 等, 词袋模型也 不适用于所有的语言, 但从计算的角度看它非常 高效.

一般地, 在将语料转换为词袋时我们需要定义 停用词 (Stop Words) 以 提升文本特征的质量, 停用词一般无法提供有价值的信息, 因此可以忽略.
在人们的日常语言交流中, 一些词语相比其他词语承载了更重要的信息, 还有一些词语的使用频率明显高于其他的词. 关于这个发现, 有 齐夫定律 (Zipf's Law):

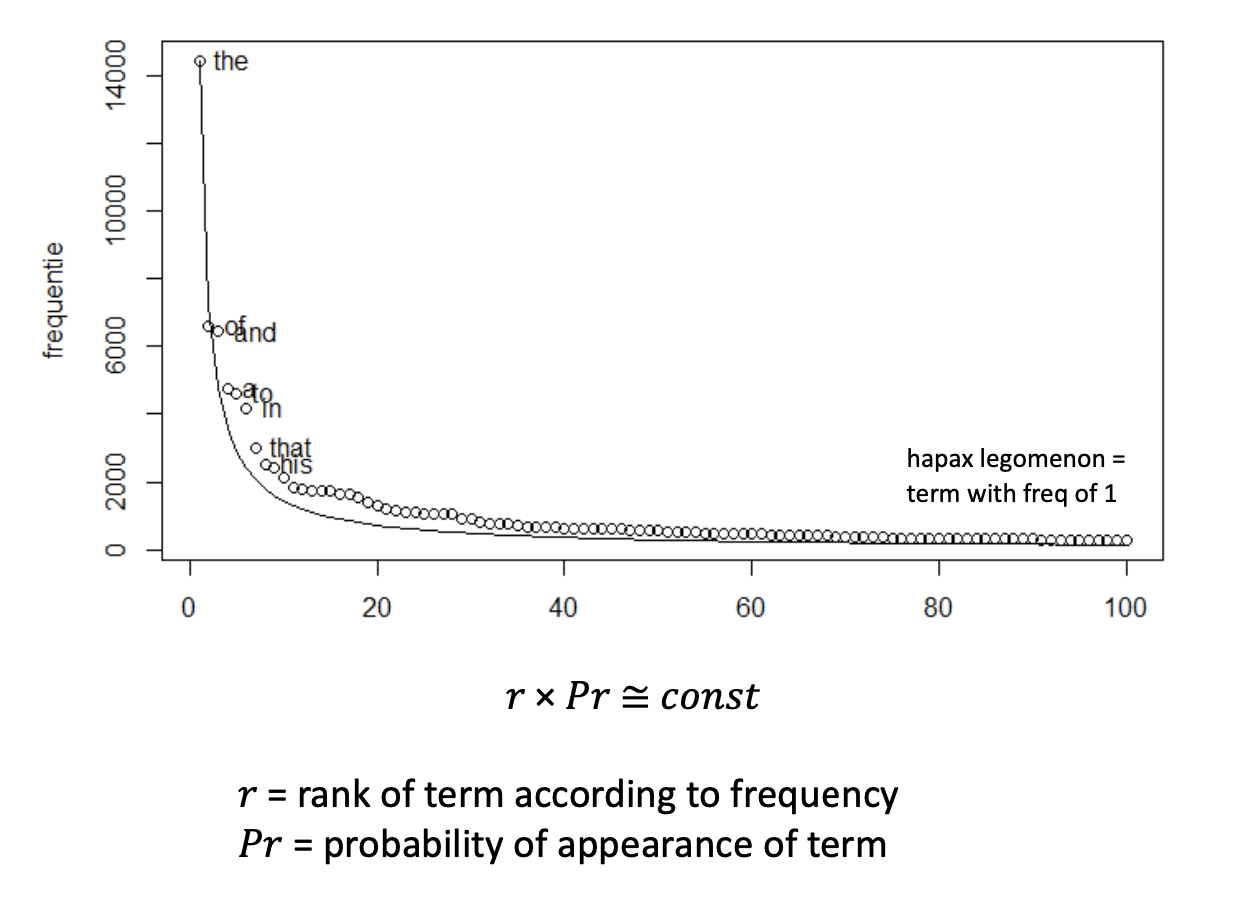
以及 卢恩假设 (Luhn's hypothesis):
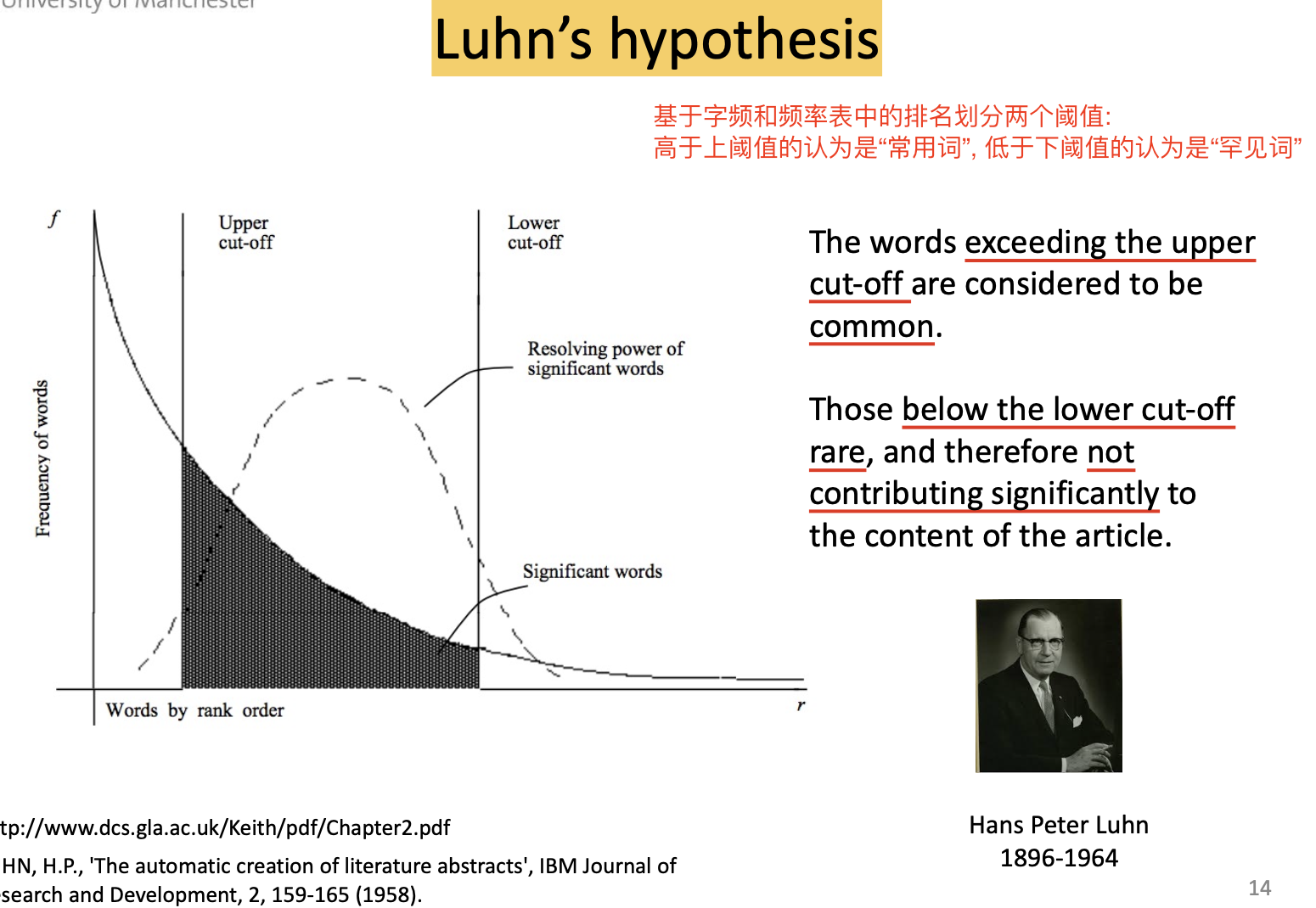
我们称这种 出现频率高, 但 信息价值低 的词为 停用词.

2.2 向量表示 (Vector Representation)
向量表示是一种 对词袋模型的实现. 我们称 词汇组 $V$ 为经过文本预处理后得到的所有项 (terms) 组成的集合, 而每个文本语料 (document) 都可表示为一个 $\vert V \vert$ 维的向量:

可见, 这样的表示是 高维 且 稀疏 的: 向量维度取决于词汇组中词汇的数量, 而并非所有的单词都会在某个句子中出现, 因此可能向量中大多数的项都是 $0$. 可见, 设定合适的停用词表可以适当地起到 降维 的作用.
向量表示中, 向量的每一个维度存储的值都是对应的词项 (term) 在这个向量表示的句子中的 发生率 (incidence), 取值在 $(0, 1)$ 之间. $0$ 表示不出现, $1$ 表示该词在句子中出现.
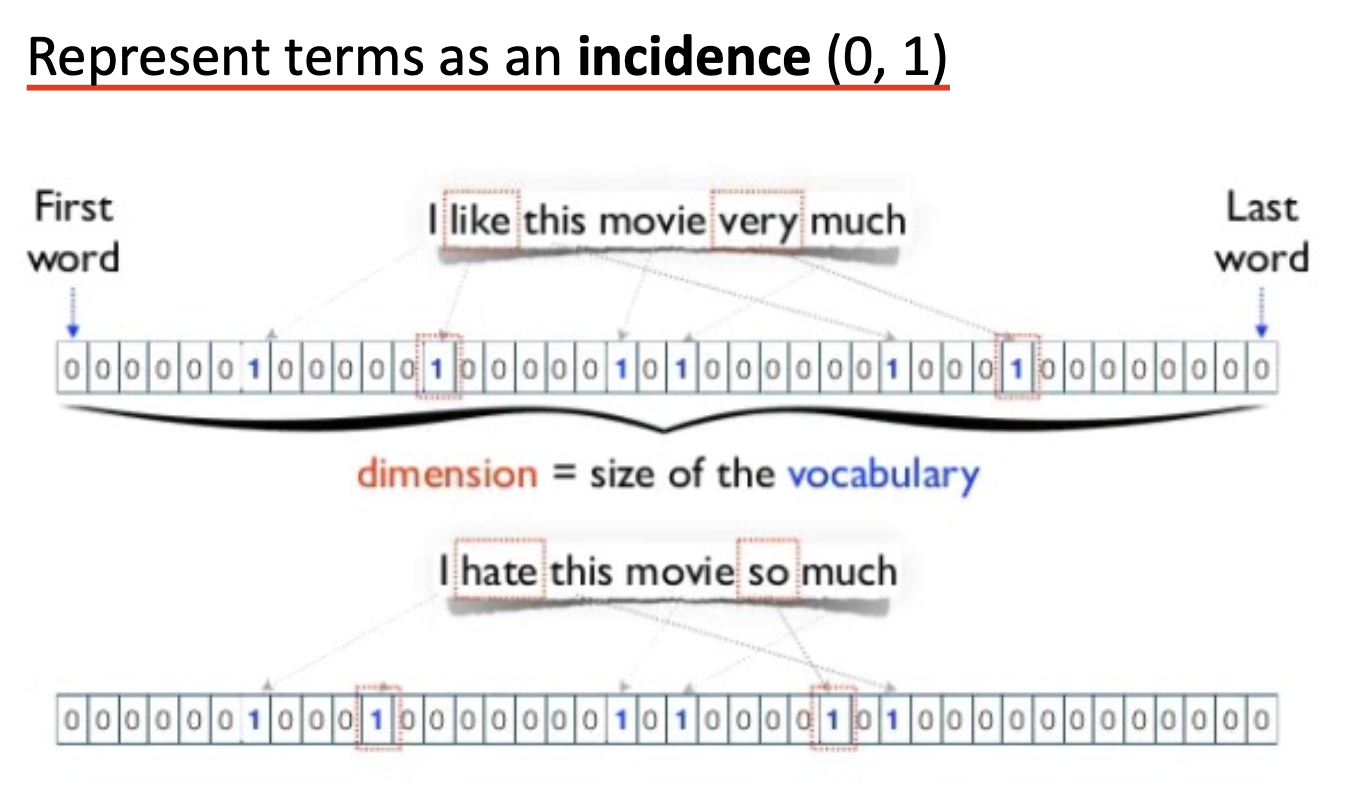
在接触了上述的 二元权重 后, 我们不难联想, 理论上也可以将 单词在句子中的出现次数 作为权重. 但 单词的重要性并不和它在句子中出现的次数成正比, 因此这样设置会导致下列的问题:

在下一章的内容中, 我们将讨论更复杂, 但更能反映单词真实重要性的权重定义方式.
总的来说, 向量表示仍然是 非常稀疏 的. 我们将在下一章中介绍 更致密的表示模型: word embedding.
在考虑 BoW 模型时, 放到 “词袋” 中的除了可以是 单独的单词 外,自然还可以是 n-gram. 回顾此前所提到的定义, n-gram 是语料中 连续的 $n$ 个单词.

除了使用词袋模型表示语料数据外, 我们还可以考虑 概率语言模型 (Probabilistic Language Models):
2.3 概率语言模型
不难看出, 在人们使用语言的过程中, 包含大量的不确定性. 我们可以使用 概率语言模型 描述和利用这种不确定性.

2.3.1 一元语言模型 (Unigram Language Model)
一元语言模型的基本假设是: 将表示为 一系列单词组成的序列 的语料 $S = w_1 w_2 \cdots w_n$ 视为一系列 彼此独立的 Unigram 组成的序列. 因此有:
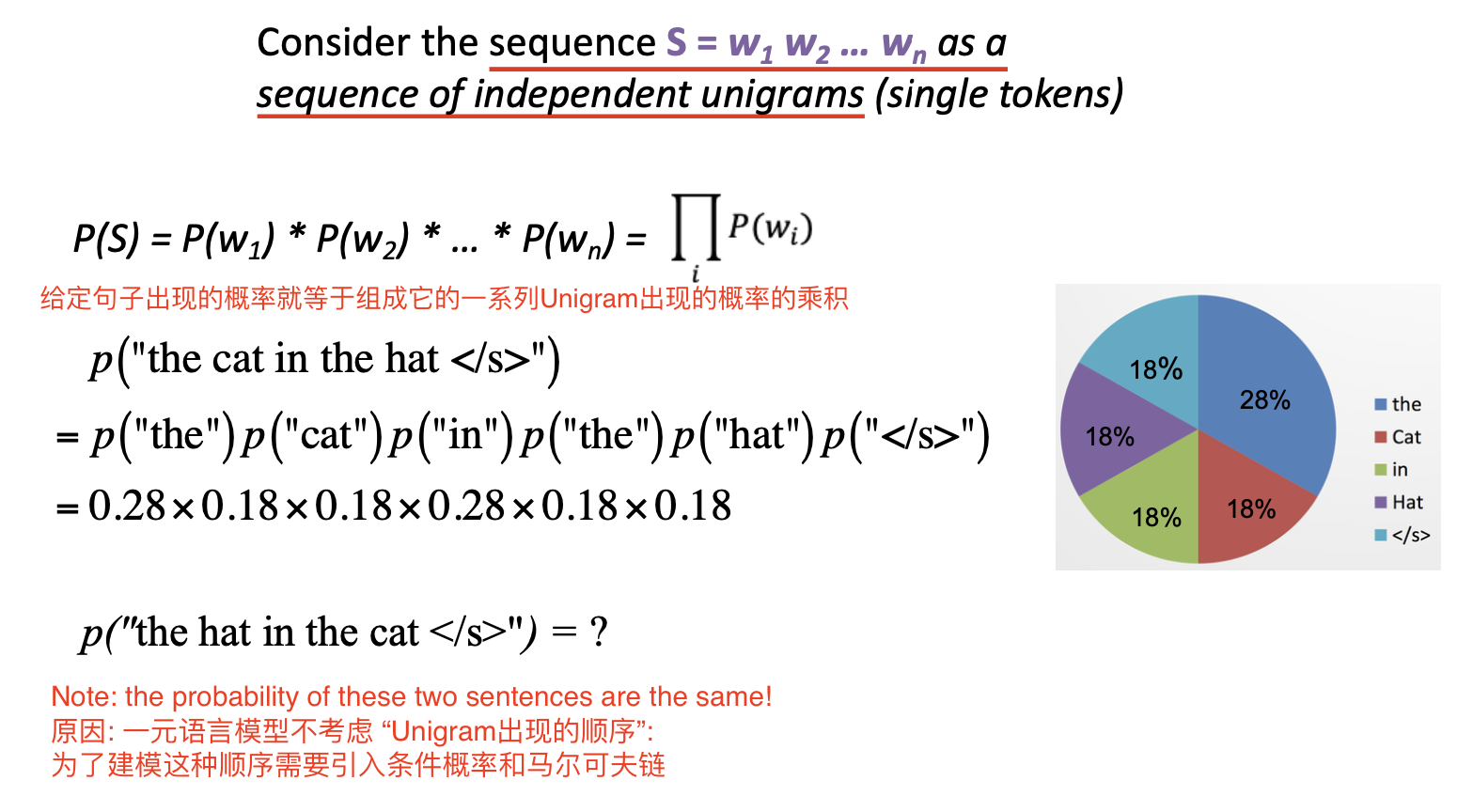
一元语言模型同样没有将 单词出现的顺序 考虑在内, 而是假设不同单词在句子中出现的顺序彼此无关, 因此它也是一种非常简单的概率语言模型. 虽然这样建模并不符合实际, 但在大多数情况下它同样具有足够良好的性能.
要计算单词出现的概率, 只需计算语料库中这个单词出现的 频率.
 ‘
‘
语料库包含的信息总是有限的, 因此需要考虑 如何处理从未在语料库中出现过的字词 的情况. 由于我们对单词出现的概率的计算是基于它在语料库中包含的频率的, 因此我们可以通过 在算式的分子和分母上同时加上一个常数 的方式 将计算出的概率平滑.

2.3.2 多元语言模型 (N-gram Model)
为了解决一元语言模型中无法准确建模 字词顺序 的问题, 我们需要引入 链式法则 (Chain Rule).
下面我们关心的是: 如何计算 一系列单词按照给定顺序出现的概率. 最朴素的思想是: 给定一系列单词 $w_1, \cdots, w_n$, 分别计算条件概率: $w_1$ 在句子开头出现的概率, $w_2$ 在 $w_1$已经出现在句子开头的前提下, 是句子中第二个单词的概率 ,等等. 也就是:

但显然基于大小有限的语料库, 我们一方面不可能得到所有这些准确的条件概率值, 另一方面对这种考虑所有情况的条件概率的计算也很复杂, 因此我们需要对链式法则进行 简化.
为了简化链式法则, 我们下面引入 马尔可夫链 的概念. 马尔可夫链 描述的是 从某个状态到另一个装态转换的随机过程, 基本假设是: 下一个状态的概率分布只由当前状态决定, 在 时间序列中 它前面的事件都和决定下一个状态 无关. 自然, 我们可以将文本或句子的生成视为一个 马尔可夫过程, 并给出 “句子中下一个单词是什么只取决于此前的一个或有限多个单词” 这一假设. 因此就有:

特别的, Bigram Model 恰好完美符合 马尔可夫链 的定义:

于是通过调整 下一个单词是什么和前面几个单词相关, 我们就可以进一步地扩展到 n-gram 模型:

对于一般的 n-gram 模型, 其条件概率仍然需要基于训练语料库进行 估计.

最简单的估计方式就是对整个语料库中, 符合条件的 occurrences 进行 计数:

而更复杂的估计方法不在本章的讨论内容之内.
