每周习题解析
Week I

回顾基本常识: B-Spline 是一种比 Bezier Curve 更强的曲线建模技术, 使用 B-Spline 方程建模的曲线首尾连接时, 接合处天然满足最强的 $C2$ 连接性 (即: 反映 tangent 的一阶导数和反映 curvature 的二阶导数都相等), 通过调整控制点即可 局部调整曲线形态, 而且控制点的数量和曲线的次数 无关, 直观区分一条曲线是被使用什么方法建模的可以直接观察曲线的两端是否通过控制点: Bezier Curve 是通过控制点的, 而 B-Spline 不是.
因此, 该题答案显然为 B.

回顾连续性的概念: C0 指视觉上两条曲线首尾相接; G1 指两条曲线在接合处切向量的方向相同; C1 指两条曲线在接合处切向量的大小和方向相等, 也就是一阶导数相等; C2 指两条曲线在接合处的一阶与二阶导数均相等, 即 Curvature 相同.
因此该题答案显然为 C.
下面讨论第三和第四题: 这两题的答案都需要使用曲线的参数化矩阵表示, 通过代入对应的 $t$ 得到坐标.

要求解这两题, 首先回顾 Bezier Curve 和 B-Spline 的 矩阵表示:

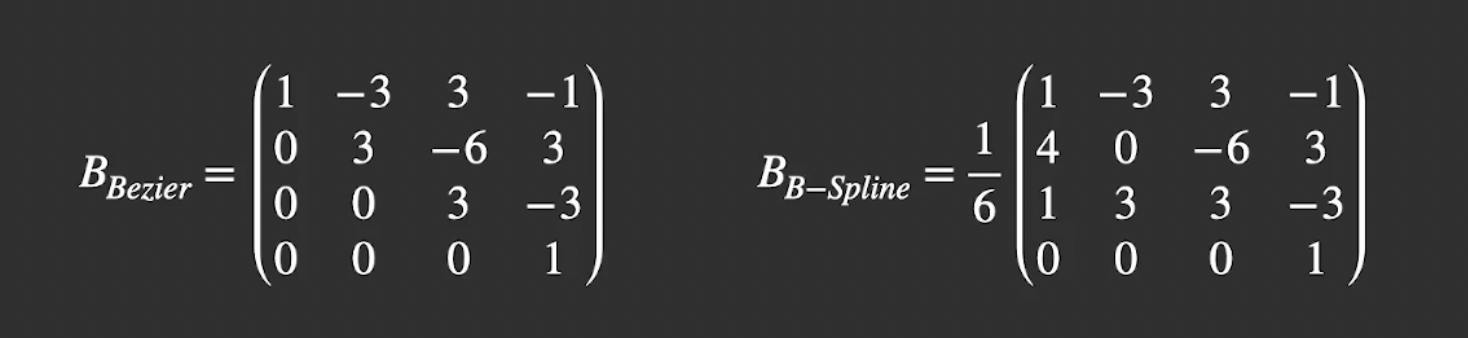
从矩阵表示中不难得到给定曲线的, 被参数 $t$ 所控制的 $x$ 和 $y$ 轴坐标的参数表达式:
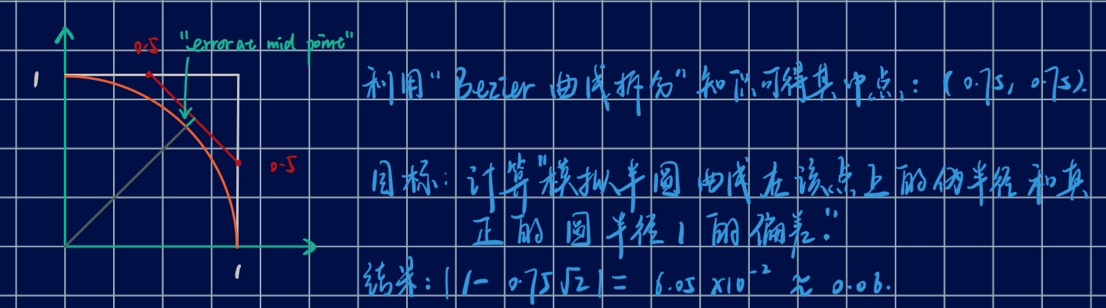
\[x = \frac{-4 + 6t + 6t^2 -4t^3}{6}\] \[y = \frac{4 + 6t - 6t^2}{6}\]因此对第三题, 分别代入终点对应的 $t=0$ 和 $t=1$ 可以分别得到坐标: $(-\frac{2}{3}, \frac{2}{3})$ 和 $(\frac{2}{3}, \frac{2}{3})$.
而对于第四题, 带入中点对应的 $t=\frac{1}{2}$ 可得到坐标: $(0, \frac{11}{12})$.

此题看图说话即可:
Week II

答案为 B. A 和 D 显然错误, C 在此处所考虑的更多是 “在游戏中创建人物” 的流水线, 和构建模型无关.

A 是正确的: 由于曲线的隐式表示形如 $F(x, y, z) = 0$, 故若要 trace a variable, i.e., 给定自变量 $x, y$ 求因变量 $z$, 不同于显式表示和参数化表示的情形可以直接得出结果, 我们需要 求解隐式表示的方程 才能得到对应的 $z$.
B 也是正确的: 通过调节参数, 我们即可修改曲面的表示.
C 符合参数方程的定义, 因此也是正确的.
D 不符合显式函数表示的定义: 显式函数表示应该形如 $f(x, y) = z$.
因此本题答案应该为 D.

A, B 是正确的: Frenet 标架的主要作用是基于曲线上的点确定关于这个点的坐标系. 回顾 Frenet 标架确定的坐标系中, 三个坐标轴分别是曲线在该点的一阶导数 切线, 二阶导数 法线 以及三阶导数 切线与法线的叉乘, 因此可以说 Frenet 标架描述了曲线的几何性质.
C 选项是错误的, 因为实际上在转折点 (Inflection Point) 处真正发生翻转的是法线 $N$, 但 这是结果而非原因. 从直接原因的角度看, $T$ 向量就是切线向量, 被曲线的一阶导数描述, 是切线向量的转折导致了法线向量的翻转.
D 选项是正确的.
综上, 本题答案为 C.
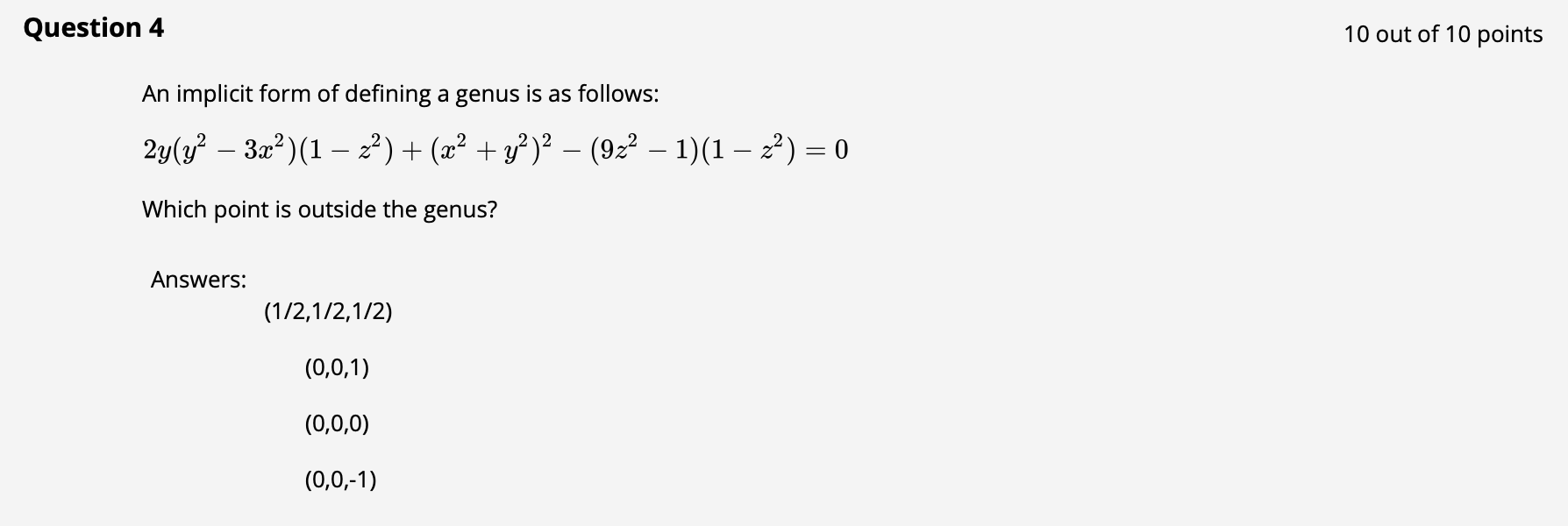
回顾曲线隐式表示的定义: 对于隐式表示 $f(x, y, z)=0$, 若代入点导致 $f(x,y,z)<0$, 说明该点位于曲线内部, 若代入点导致 $f(x, y, z)=0$, 说明该点在曲线上, 若代入点导致 $f(x,y,z)》0$ 可知代入点在曲线外. 由此可知: 因为 $(0, 0, 0)$ 时表达式值为 $1$ 大于 $0$, 符合 “位于曲线外” 的情况. 故本题选 (0, 0, 0).

A 错误: 使用双三次贝塞尔表示法表示的曲面控制点数量是 $16$ 个.
B 错误: 向网格中添加新的点和边都非常方便.
C 正确: 任何情况下使用任何方式建模的曲面最后在渲染管线中都会被栅格化.
D 错误: Displaced Surface 是凹凸不平的, 因为平面上的点的高度会基于 Displacement Map 中存储的 offset 被抬升对应的高度, 形成 凹凸不平 的曲面.
故本题答案为 C.
Week III

在构造物体运动的动画时, 对物体加速度程度的建模基于它的 质量.

Rigging: 绑定, 构造骨骼约束.
Skinning: 蒙皮, 将骨骼和模型结合起来: 把 “蒙皮” 上的关键点映射到骨骼的对应位置上.
Tweening: 自动插值补全关键帧间的动画, 又称补间.
Posing: 将模型摆出特定的姿势.
基于题意可知, 在完成 Rigging 后下一步自然需要进行蒙皮操作.

色度图 (Chromaticity Diagram) 是从完整的色彩空间 拍扁到二维平面上 得到的, 因此它 不包含明度信息. 由此可知, 在更改颜色的亮度后, 它在色度图中的坐标 不变.

物体的颜色取决于它 不吸收什么波长的光, 若一个物体看上去为白色, 说明它 不吸收任何波长的光. 若某个物体吸收 所有波长的光, 则它看上去应该是 纯黑色. 其余选项均正确.

第二个视频中已经说明, 电影行业的帧速率标准 (大概) 为 $24\text{fps}$, 对视频而言 $30\text{fps}$ 已经够用, 视频网站, 手机和相机的默认视频播放/录制帧速率都是 $30\text{fps}$. 对于 VR, 为避免眩晕, 内建的显示屏需要提供至少 $90\text{fps}$ 的刷新率.
Week IV

注意: Rigging 是指为模型添加骨架的过程, 而 Skinning 是指将模型的表面贴图绑定到模型已有的骨架上的过程.

动作捕捉技术可以直接记录现实中物体的运动轨迹, 本质上相当于 “让现实的物理规则帮我们计算物体的运动, 白嫖大自然的算力”, 因此可以实现绝对贴近真实的效果.

该二阶微分方程描述了给定粒子的运动情况. 显然, 由于该粒子受两个作用力: 重力 $mg$ 和阻力 $dv$, 其受到的合力可以记为 $-mg-dv$. 由 加速度是速度的一阶导数 可知:
\[\frac{dv}{dt} = \frac{dx}{dt} \cdot \frac{d}{dt} = \frac{d^2x}{d{t^2}} = -g - \frac{dv}{m}.\]
由上一题的结论, 显然可得出正确答案.
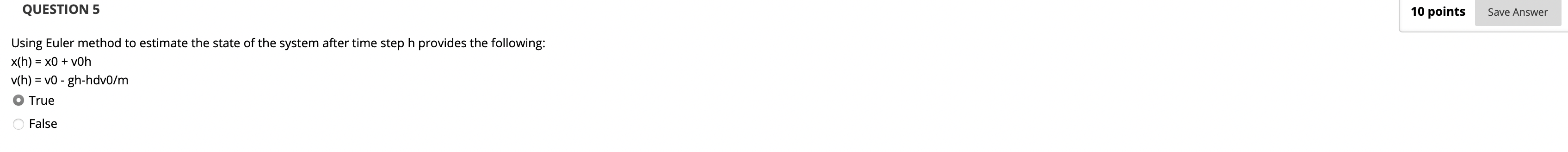
注意欧拉法假设在考虑的这段极小的时间内物体的速度不发生变化, 因此沿用当前时刻物体速度的大小和方向, 预估极小时间变化内物体位移的变化. 由此可知, 给定的方程显然属于欧拉法的方程.
Week V

注:
hinge joint: 1 degree of freedom, (therefore when forming a hinge joint you need to decrease for 5 dofs)
ball joint: 3 degree of freedom (rotational), (therefore when forming a ball joint you need to decerase for 3 dofs)
universal joint: 2 degree of freedom (also rotational), (therefore when forming a universal joint you need to decrease for 4 dofs)
肩膀处的关节属于球状绞接关节. 如果实在难以想象, 请回忆一下鸡锁骨的结构.
有限元法适用于任何可形变物体的模拟, 弹簧模拟更适合模拟布料而非液体. 网格模拟的 Eulerian Fluid Simulation 和粒子模拟的 Lagrangian Fluid Simulation 是两种常用的流体模拟方式, 因此在这些模拟方法中需要选择相对最不合适的 弹簧模拟法.

考虑上述多种构造碰撞检测箱的算法时, 要确认它们的复杂程度级别只需回忆下面的图即可:
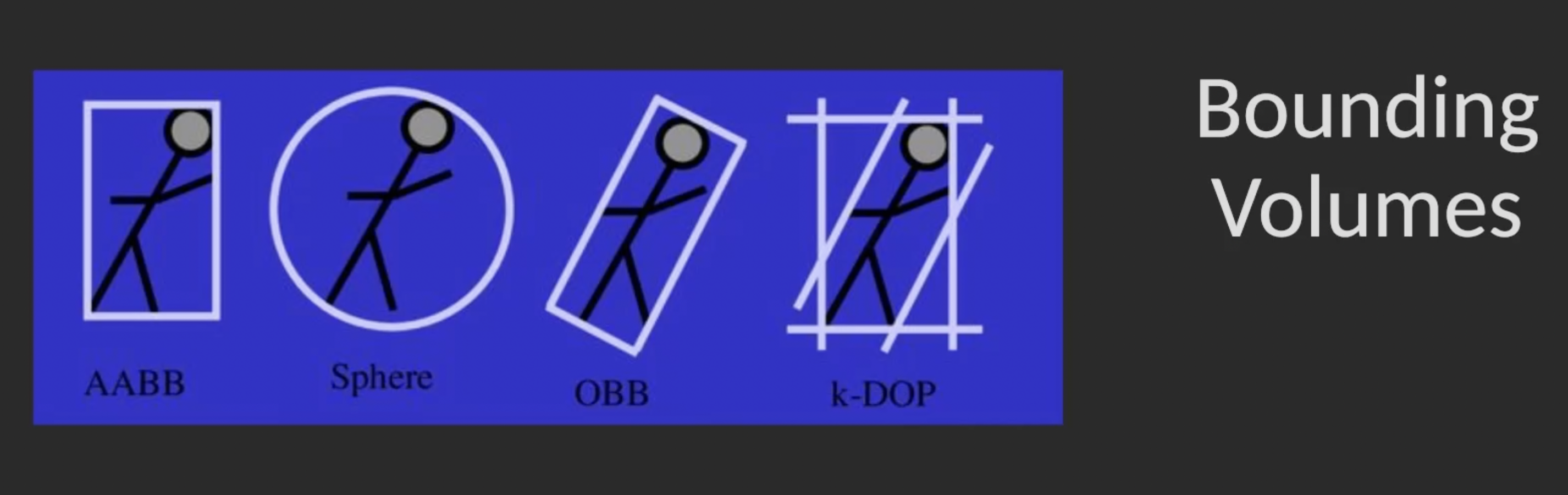

在考虑 $N$ 个物体之间的碰撞时, 任何两个不同的物体都需要检测一下, 因此总共需要执行 $\binom{N}{2} = \frac{n^2-n}{2} \in O(n^2)$ 次检测.
注意: 这也是本课程最后介绍的 Hierarchical Bounding Volume 的优点之一.
Week VI

渲染方程的一大重要假设就是: 在场景的某个点上观察到的光是该点自身发出的光和从所有其他点射到此处的所有光的合成. 由于可见光也可视为能量辐射, 因此这对应热力学第一定律: 物体内能的增加等于物体吸收的热量和对物体所作的功的总和.
渲染方程只关心 观察点到被观察点之间的角度, 并未真正考虑观察点的具体位置.

基于 Lambert Law 可知: 入射光线恰好垂直于平面时, 光强最大.

原因正确但结论不对: 在第一个视频的末尾提到, 正是因为渲染方程是 Fredholm Equation of Second Kind, 因此我们无法求出它的分析解.

a) 为我们从观察点所观测的, 目标点发散出的能量辐射 (Radiance), b) 为该点自身发散出的能量辐射 (Radiance), d 为不同方向上射入目标点的能量辐照 (Irradiance).
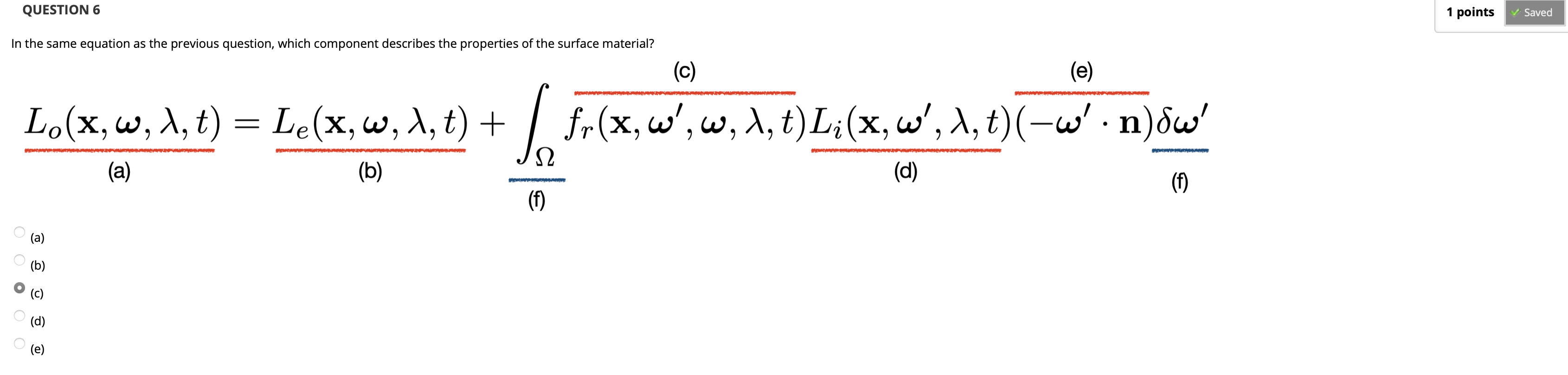
此题显然, 不做解释.

原因正确但结论显然错误. 项 e) 是 Lambert Cosine Law Factor.
Week VII

答案显然, 回顾基础定义: 用于确定平面上的给定点是否能够接收来自任何光源的光照的光线是 “Shadow Feeler”, 它的指向必 直接朝向场景中光源的方向.
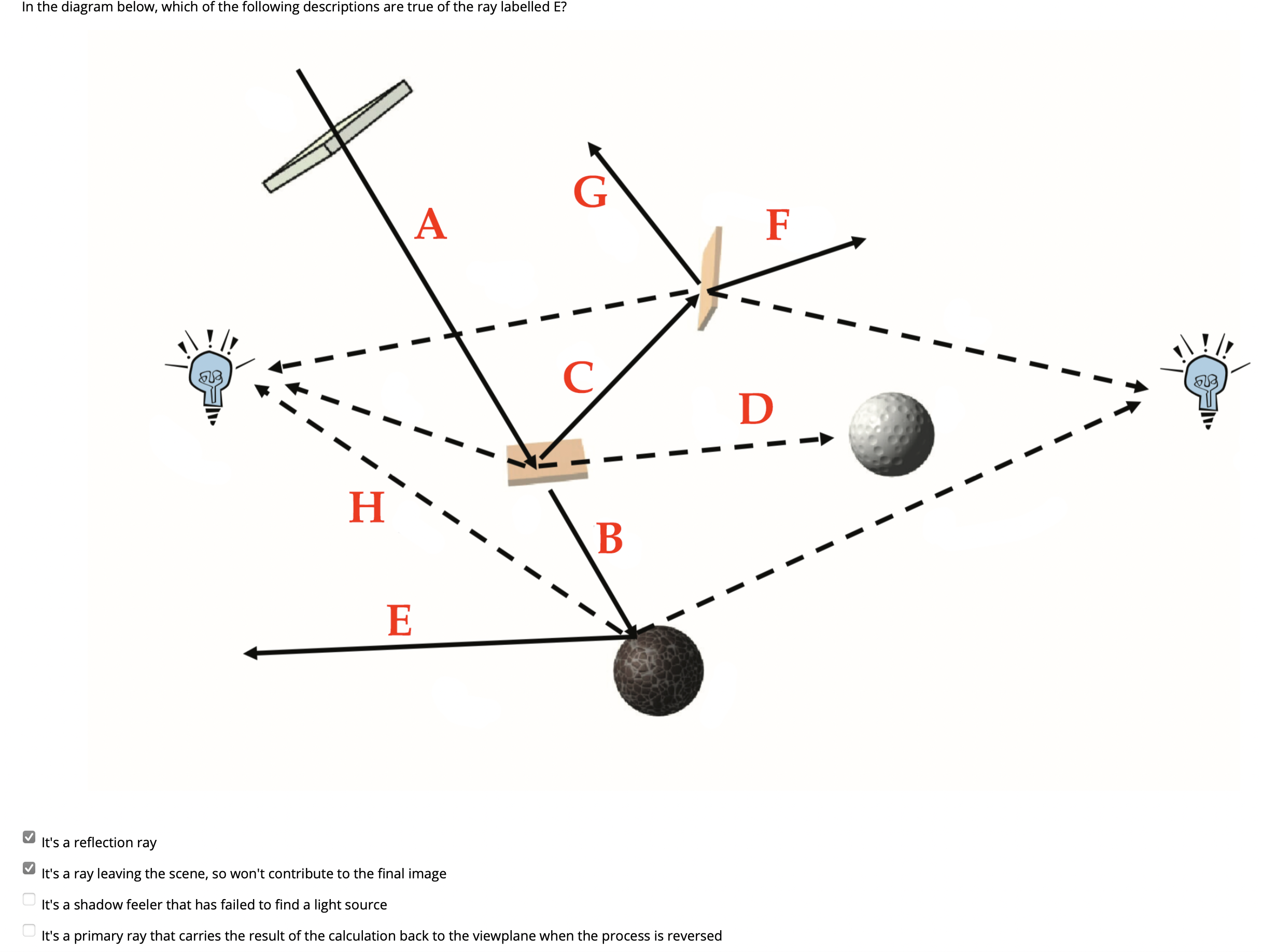
首先, 显然可以确认光线 E 是一条 反射光线, 并且它并不是 Shadow Feeler, 因为它并不直接指向场景中的任何光源. 此外, 在整个场景中只有 A 满足 Primary Ray 的定义: 直接从视平面中射出的光线. 由于此光线射出了场景之外, 既不是包含局部光照信息的 Shadow Feeler, 也没有再和任何物体交互, 也不会改变原光线的颜色, 因此可以确定它不会对最终场景有任何实质影响.
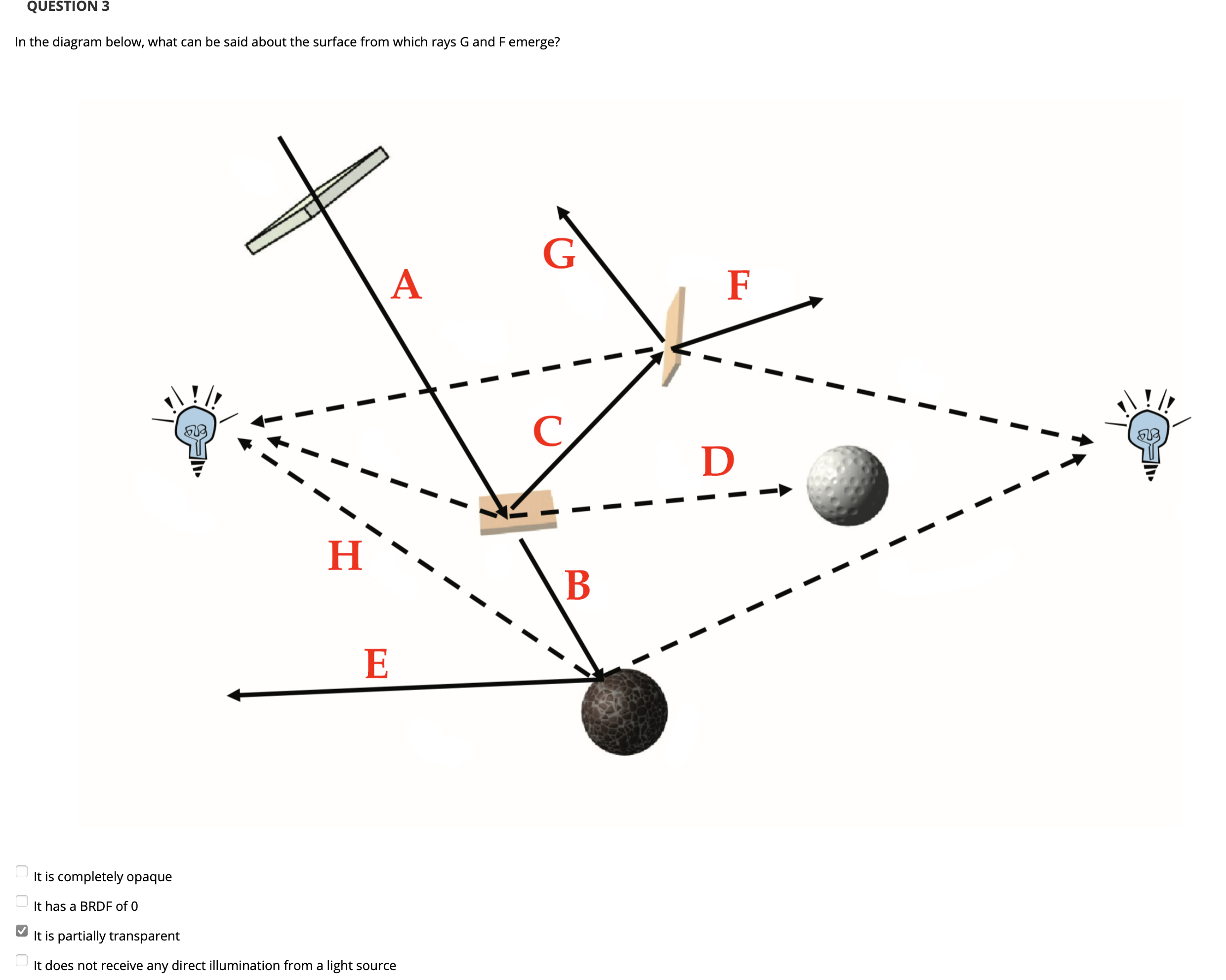
显然对于光线 G 和 F 交汇的平面而言, 可以看出入射光线 C 与其交互后射出的两条 Shadow Feeler 都打到了场景中的两个光源上, 说明该平面是可以接受场景中光源的直接光照的. 此外, G 和 F 实际上分别是入射光 C 的 反射光 和 折射光, 因此说明该平面 既不是完全不透明的, 也不是 会吸收所有光, 即 BRDF 为 $0$ 的.

个人认为这题的答案有问题, 应该是 irradiance flux.

基础概念题, 不做解释.

Form Factor 是描述两个面之间是否存在 遮挡 的量, 在确定 Form Factor 时显然考虑物体表面的材质不会有任何实际意义.

此题的语言描述极其不严谨: 在此处它所考虑的应该是 “光线追踪和辐射着色这两种方法间, 只能被辐射着色实现的效果有哪些”. 因为实际上, color bleed 是可以被路径追踪所实现的. 这是由于在第七周时我们还没学到路径追踪, 因此题目假设我们只会在传统光线追踪和辐射着色之间考虑. 希望考试时不要出现如此不靠谱的题目…
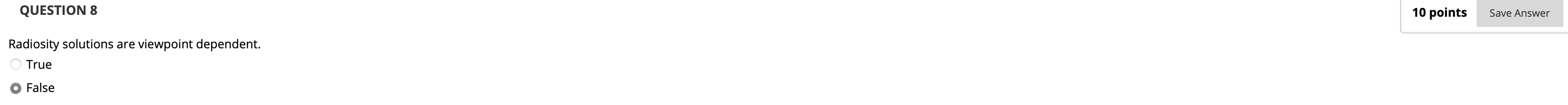
由于辐射着色是对整个场景中平面之间的辐射状态进行建模, 因此它的结果是与视点位置无关的.
Week VIII

传统的光线追踪首先可以实现所有的 Specular 效果和 Hard Shadow. 其次, 由于它以 确定性 的方式对光线的传播路径进行绝对精确的追踪, 因此它可以同时渲染出反射 (Reflection) 和折射 (Refraction) 效果. 最后, 在 nVIDIA 的视频 $7$ 中, 明确提及传统光线追踪也可支持类似丁达尔效应的 Participating Media 和视觉景深效果.

辐射着色的效果与任何 Specular 效果无缘. 在此基础上, 由于它的渲染逻辑基于 “物体表面之间的辐射交换”, 因此自然具有渲染出 Color Bleed 和 Diffuse Interreflection 的能力. 此外, 辐射着色渲染出的影子自然具有柔和的边界.

路径追踪具有上述的全部性质.

在只使用 BRDF 结合渲染方程对场景进行渲染时, 首先由于没有考虑 BTDF, 因此自然无法渲染折射 Refraction. 其次, 由于缺乏光线追踪或路径追踪对视觉景深的模拟, 单纯使用 BRDF 无法渲染出景深. 同样, BRDF 无法渲染出 Relativistic Effect. 最后, 由于 BRDF 是基于热力学的, 它自然也无法渲染 冷发光效果 (Luminsense).

注意: 纹理烘焙技术本身不依赖于视点的位置: 即便改变视点位置也不需要重新烘焙纹理贴图. 但烘焙到纹理贴图中的信息只有结合特定的视点位置才能得到最佳效果, 因此一旦移动视点, 纹理烘焙就无法再模拟物体表面的平滑高光, 平滑反射或折射, 而纹理烘焙技术更不可能模拟景深.

采样不足的话会导致渲染出的场景具有两个问题: Noisy 和 Inaccurate.

显然, 增加每个像素的采样数会导致计算复杂度随着像素数量 线性 增加, 也就是随着视平面的大小而增加: 视平面越大, 包含的像素数就越多.
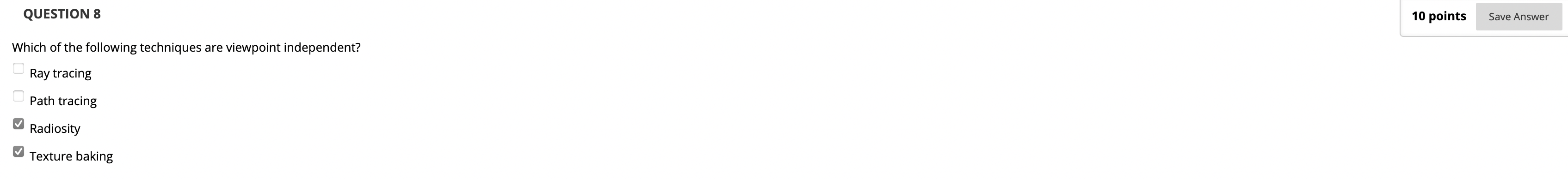
作为基于热力学的渲染方法, 辐射着色自然与视点位置无关. 而变换视点位置也不会导致我们不得不重新烘焙纹理贴图, 唯一的后果就是让效果变得不真实.
Week IX
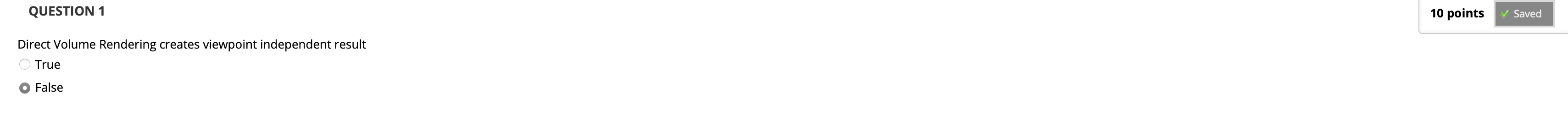
回顾直接体积渲染的相关知识: 由于直接体积渲染中包含类似于 ”光线的路径追踪“ 的流程, 因此它的渲染结果是 Viewpoint-Dependent 的. 不过需要注意: 在渲染前对 Volume Set 中每个 Voxel 的颜色和透明度的计算是 Viewpoint-Independent 的, 因为它只基于我们的实际观测需求和所有 Voxels 中数值的分布情况.
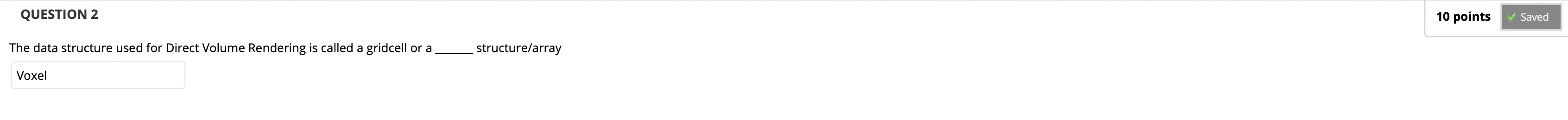
直接体积渲染以来的数据结构是 Voxel Array, 也称为 Volume Set.

原始数据中每个 Voxel 存储的数值可以是使用任何测量手段得到的, 关于物体的某种测度, 不局限于频率, 密度等; 如第一题的解释中提及的一样, 颜色和透明度在视角变换时无需被重新计算.

回顾间接体积渲染中, 使用 Marching Cube 方法计算 ISO Surface 所存在的问题: 由于 Ambiguity, 我们计算出的曲面多边形很可能是不真实的. 即便使用 Proxy Geometry, 在视角变换时也 不一定非得重新计算切片, 只不过不计算的话会使视觉效果不真实而已.

多边形网格可以直接用于执行常规渲染, 执行体积渲染需要提供对物体的某种测度.
Week X

Gridcell 背后的数据结构是 $3$ 维数组.

$3$ 维数组的访问时间复杂度是 $O(1)$.
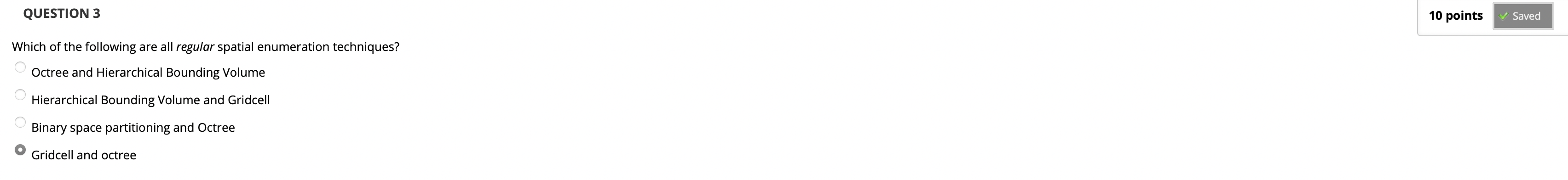
Gridcell 和 Octree 的索引构建过程都是基于给定规则的.

Binary Space Partitioning 分划可以保留空间中的相对前后, 上下和左右关系.
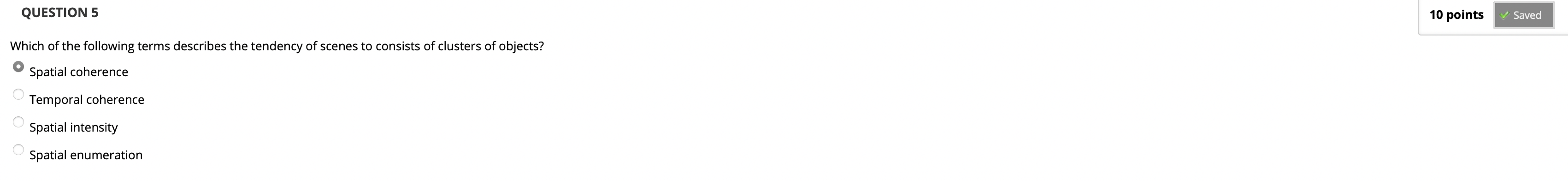
不做解释, 概念题.

注意此处的 “Projected winding”, 这意味着多边形已经被渲染, 从而意味着此时再进行检测起到的仅是类似 z-buffer 的作用, 因此无法对渲染时间的提升起到有价值的帮助.
