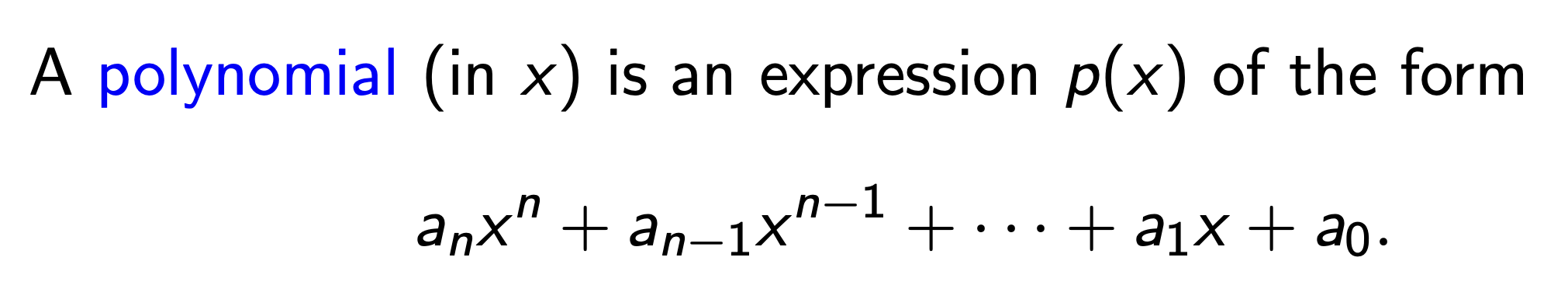时间复杂度层级和字符串查找算法

!!注: 完整详细的复习内容请参阅 《COMP36111 期末总复习》.

本章将介绍更高的时间复杂度层级, 证明并查算法的时间复杂度为常数级别, 并介绍数种字符串查找算法.

Fast and Slow: 时间复杂度层级

在本节中, 我们将首先介绍数种 增长速度不同 的函数定义, 并进一步证明: 上一章中最后介绍的 Optimized Union-Find 算法的时间复杂度是 几乎线性 的.

定义 (多项式)

称以 $x$ 作为自变量, 具有下图所示的形式的关于 $x$ 的表达式为 多项式:

定义 (多项式有界)

对函数 $f: \mathbb{N} \rightarrow \mathbb{N}$, 若存在某个 多项式 $p$, 使得:

\[\forall n, f(n) \leqslant p(n)\]

则称 $f$ 是 多项式有界 (Polymonially Bounded) 的.

类似地, 我们还可定义 指数有界, 双指数有界, 以及更高的 $k$-倍指数有界:

注意 $k$-倍指数有界的定义:

不难看出有以下结论:

1. $2^n$ 不是多项式有界 的, 但它是 一次指数有界 的.
2. $2^{n^2}$ 是 单指数有界 的.
3. $2^{2^n}$ 不是 一次指数有界 的, 但它是 二次指数有界 的.
4. 对于 $n!$, 只要 $n$ 足够大 (大于 $2$), 则它是 一次指数有界 的: $2^n < n! = 2^{n\log{n}} < 2^{n^2}$.

我们下面介绍一些增长 非常迅速 的函数:

塔函数 (Tower | Tetration Function):

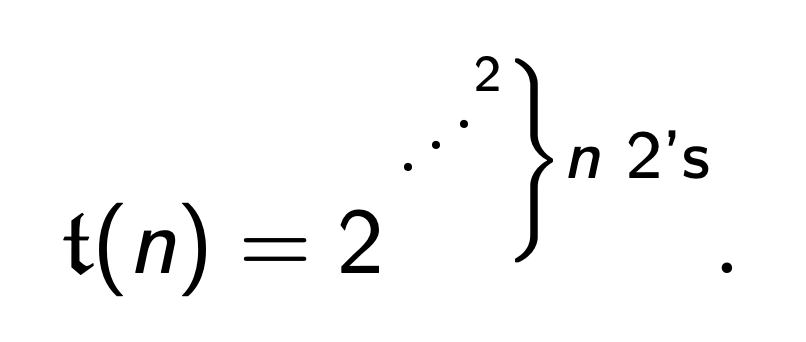
我们用下列的简化脚本语言 LOOP 描述塔函数:

在 LOOP 语言中我们只考虑下列所示的语法:

则分别有:

可见, 使用简单的嵌套循环就能得出 $n$ 阶塔函数的实现, 理论上这样的构造可以一直持续下去.

由此我们构造一套 函数时间复杂度的分级机制:

因此可知:

Ackermann 函数

Ackermann 函数是一种 递归定义, 增长速度 更快 的 非原始递归 函数. 它是如下定义的:

其中, 我们用下列所示的表述来描述 “对变量 $x$ 应用了 $k$ 次的 Ackermann 函数”:

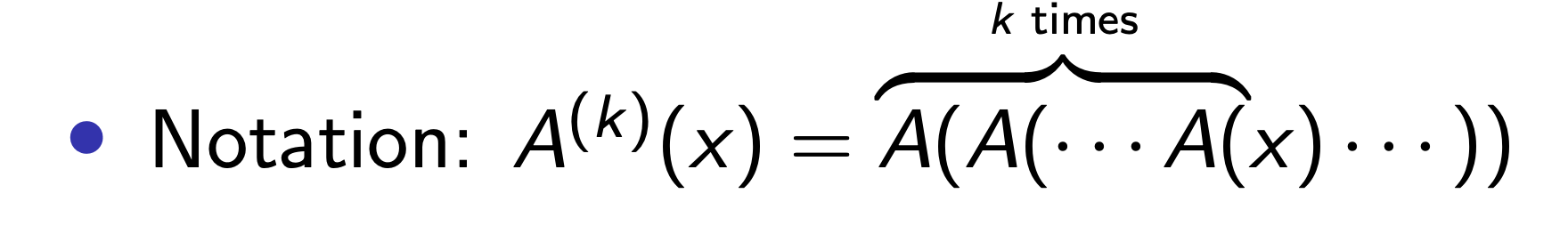
由于 Ackermann 函数可被解释为 映射, 因此作为函数, 它自然有自己的 反函数.

Ackermann 函数的反函数记为 $\alpha(n)$. 它接受输入 $A(x)$, 输出 $x$. 换言之:

证明优化的并查算法的时间复杂度为常数级别

在介绍了必要的工具后, 我们下面开始对 优化的并查算法的时间复杂度为常数级别 这一结论给出证明.

定理

使用 树 数据结构实现的并查算法 union-find(G=(V,E) 的时间复杂度为 $O((n+m)\alpha(n))$

其中 $n=\vert V \vert$, 而 $m=\vert E \vert$.

证明

字符串查找算法

本节讨论字符串中 子字符串 的搜索问题. 我们将首先完成 问题描述, 然后依次介绍三种解决问题的算法: 最简单的弱智算法, Rabin-Karp 算法和 Knoth-Morris-Pratt 算法.

问题描述

字符串查找问题是指, 给定一段文本和一小段需要被查找的字符串, 要求在这段文本中对字符串进行查找. 如果这段字符串在文本中存在, 需要给出它在文本中的 位置, 反之需要返回 “目标字符串不存在” 这一结果.

我们首先对问题建模:

弱智算法

解决字符串查找问题的最简单的想法是: 既然要被查找的字符串 $P$ 的长度为 $\vert P \vert$, 则可以 遍历 文本 $T$ 中从 $0$ 到 $\vert T \vert - \vert P \vert$ 的位置作为 可能的起始位置, 然后对于每个可能的起始位置再去遍历长为 $\vert P \vert$ 的字符串序列, 看看它是否和要被查找的字符串相同.

显然, 这是一个两层嵌套的循环, 时间复杂度为 $O(\vert T \vert \cdot \vert P \vert)$.

Rabin-Karp 算法

Rabin-Karp 算法的基本思想是: 仿效哈希表中使用数字对字符串编码的方式, 对文本和目标字符串都进行编码, 然后利用编码的数学性质进行检查和搜索. 其具体实现如下:

回顾我们有三个基本元素: 文本 $T$, 目标字符串 $P$ 以及定义文本和字符串的 字母表 $\Sigma$.

我们分别取字母表, 文本和目标字符串的 长度 (大小): $b = \vert \Sigma \vert, n = \vert T \vert, m = \vert P \vert$.

然后我们可以将字母表中的每个字母分别赋予 以字母表大小 $b$ 为底的计数系统中的编号, 比如: 如果某个字母表中有 $16$ 个字母, 则依次对它们赋予 $16$ 进制中的不同编号.

然后给定一个字符串, 比如这里就直接考虑目标字符串 $P$, 它就可被表示为:

相应地, 文本 $T$ 就可被表示为:

然后文本 $T$ 的一个长为 $m$ 的 分段 就可表为:

这样我们就得到了:

1. 目标字符串 $P$ 的 唯一表示
2. 文本 $T$ 中 可能和目标字符串匹配的一个长为 $m$ 的分段的唯一表示

这样的话通过对比它们的唯一表示就可确定 它们是否相等.

而这种表示方式的优越性在于: 在文本上 “移动观察窗口” 时, 无需进行多余的重复计算:

假如我们现在已经计算出了位置在 $i$ 到 $i+m-1$ 的子串 $T[i, \cdots, i+m-1]$, 要计算观察窗口向右移动一个字符后得到的子串 $T[i+1, \cdots, i+m]$ 就只需要进行以下的计算即可:

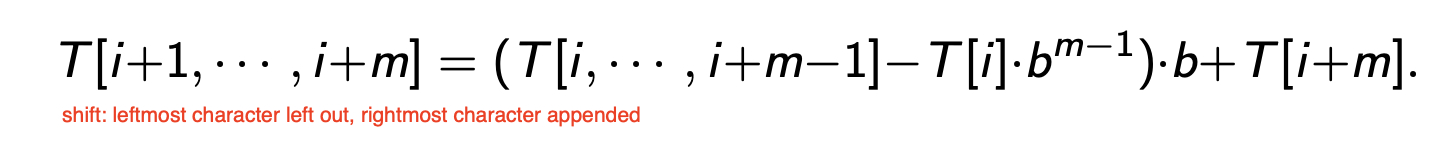
当然, 如果我们直接使用计算出的直接结果, 我们会不可避免地需要比对两个 可能很大的数. 但我们可以 通过对计算结果取模 $q$ 后的结果避免这个问题.

改算法在 最坏情况下 的时间复杂度仍然是 $O(\vert T \vert \cdot \vert P \vert)$. 但如果考虑平均情况: 出错, 也就是 计算出文本中某个子字符串的数字表示和目标字符串一致, 但实际上它和目标字符串不同 的概率是 $\frac{1}{q}$.

而在整个文本中, 首先只要我们找到一个真正的匹配, 就无须继续寻找剩下的, 因此可以在这里停止; 其次, 最坏情况下出现这种问题时需要特别处理, 所耗费的时间复杂度为

因此在平均情况下该算法的时间复杂度为

也就是大概

因为一般来说字典的大小 $q$ 可能比目标字符串的长度 $m$ 要大.

算法的伪代码如下:

Knoth-Morris-Pratt 算法

我们最后讨论相对最优的 KMP 算法.

KMP 算法要解决的问题仍然是 主串中的字符串匹配问题.

它的基本逻辑是: 我们在进行匹配时所找到的第一个不匹配的位置实际上已经包含了 “指针应该跳转到的下一个方向” 的信息, 通过利用这个信息, 保持主串 (也就是文本 $T$) 的指针不回溯, 通过修改 目标字符串的指针, 让它尽可能地移动到有效的位置, 我们就可以减少尝试次数, 降低时间复杂度.

KMP 算法中目标字符串的指针的移动规律

下面首先来探究目标字符串中指针 $j$ 的移动规律:

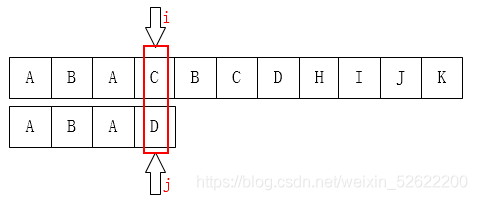
通过对比两个指针 $i$ 和 $j$, 可以看出此时字符不匹配. 如果控制 $i$ 指针位置 不变, 移动 $j$ 指针, 最合适的位置自然是 目标字符串的第 $1$ 个位置 $B$ (从 $0$ 开始编码位置), 因为不难看出在对应的位置都有一个 $A$, 可以无需比较.

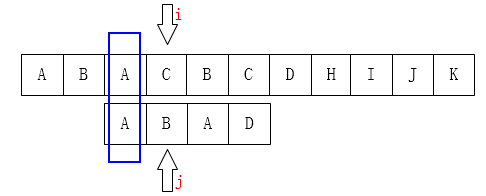
在这里可以看出: 需要被移动的目标位置 $1$ 的前后 $1$ 个位置范围内: 位置 $0$ 和后面一个位置 $2$, 都有 相同的字符.

下面看一个更复杂点的例子:

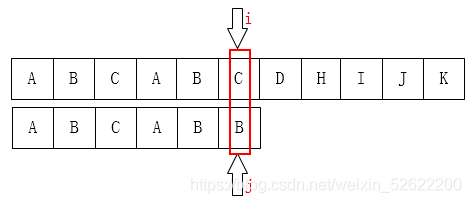
此时不难看出 $j$ 应该被移动到的合适的位置是 $2$, 并且位置 $2$ 前后 $2$ 个位置范围内都有相同的字符.

从上面的两个例子中大致可以看出, 当字符串匹配失败时, 子字符串的匹配指针从当前位置 $j$ 所需要移动到的下一个位置满足这样的性质:

从这个位置往前数, 一直数到头, 假设数了 $k$ 个字符, 则从 $j$ 这个位置往前数, 也数 $k$ 个字符, 它们应该是 一样的.

用公式来表示的话就是这样:

1
P[0 : k-1] == P[j-k : j-1]

经过简单思考即可得知, 我们将指针从 $j$ 移动到这样的新位置的正确性. 如果我们从 $0$ 开始标记字符串序列的每个位置, 那这个操作就等同于: 将指针 $j$ 移动到 $k$ 而不再比较前面的 $k$ 个字符.

算法的伪代码如下:

KMP 算法中对目标指针下一个最适位置的计算

下面我们需要考虑的问题是: 如何求出这些新位置 $k$.

由于我们将在完全未知的文本中匹配目标字符串 $P$, 因此在 $P$ 的 每一个位置上 都可能发生 “从此开始不再匹配” 的问题. 也就是说, 我们需要计算 $P$ 中每一个位置 $j$ 所对应的 “指针移动到的下一个位置 $k$“.

同样, 我们首先从例子出发探究计算思路. 在这里我们用 $\pi$[j] 表示, 当 $P[j] \neq T[i]$ 时, 指针 $j$ 的 下一个移动位置.

首先考虑一个 edge case: 指针 $j$ 已经在目标字符串的第 $0$ 个位置, 此时它 无法再移动, 因此只有让 $i$ 指针 后移:

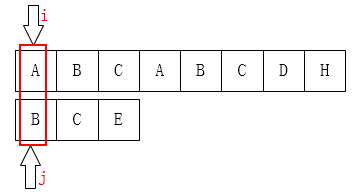
而当指针 $j$ 在目标字符串的第 $1$ 个位置时, 它只能前移到第 $0$ 个位置:

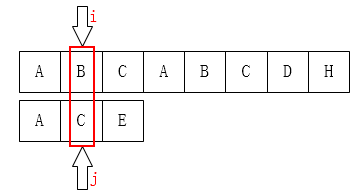
并且可以发现: 当 $P[k] = P[j]$ 时, 有

这是因为, 在 $P[j]$ 前已经有相等关系:

而此时又有

因此满足

也就是

所以

该关系如下图所示:

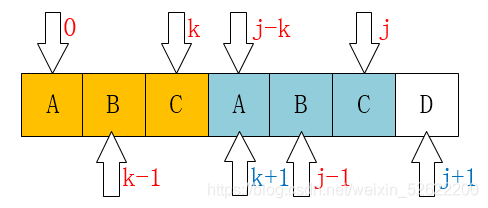
而在 $P[k] \neq P[j]$ 的情况下, 应该跳过当前得到的 $k$, 反而去进一步取 $\pi(k)$.

由此对 “存储下一位置 $k$ 的矩阵” 的计算方法如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def compute-pi():
    p = list(p)
    next = [-1 for _ in range(len(p))]

    j, k = 0, -1

    while (j < len(p)-1):
        if (k==-1 or p[j] == p[k]):
            j = j+1
            k = k+1
            next[j] = k
        else:
            k = next[k]

    return next

REF: https://blog.csdn.net/u012948161/article/details/126241717

https://blog.csdn.net/weixin_52622200/article/details/110563434

最后给出结论: KMP 算法的时间复杂度是 $O(\vert P \vert + \vert T \vert).$

• Previous
  高级计算机图形学:曲面建模理论
• Next
  高级计算机图形学:每周习题解析