曲面建模理论
在上一章中, 我们讨论了建模曲线的主要方法, 本章主要介绍对 曲面 的一般建模方法.
Triangle Mesh 三角网格是表示 平面 的主要方式, 它通过将三角形的网格拼接来模拟平面.
此外, 通过基于原始的三角网格构造 细分曲面 (Subdivision Surface), 可以得到相对平滑但仍然粗糙 (Coarse) 的曲面表示.

上图所示的两个兔子模型从左到右分别是基于三角网格生成细分曲面的表示, 以及使用三角网格的表示.
另一种模拟曲面的方式是 张量积样条 (Tensor Product Spline), 它基于样条 (Spline) 模拟某个曲面, 如下图所示.
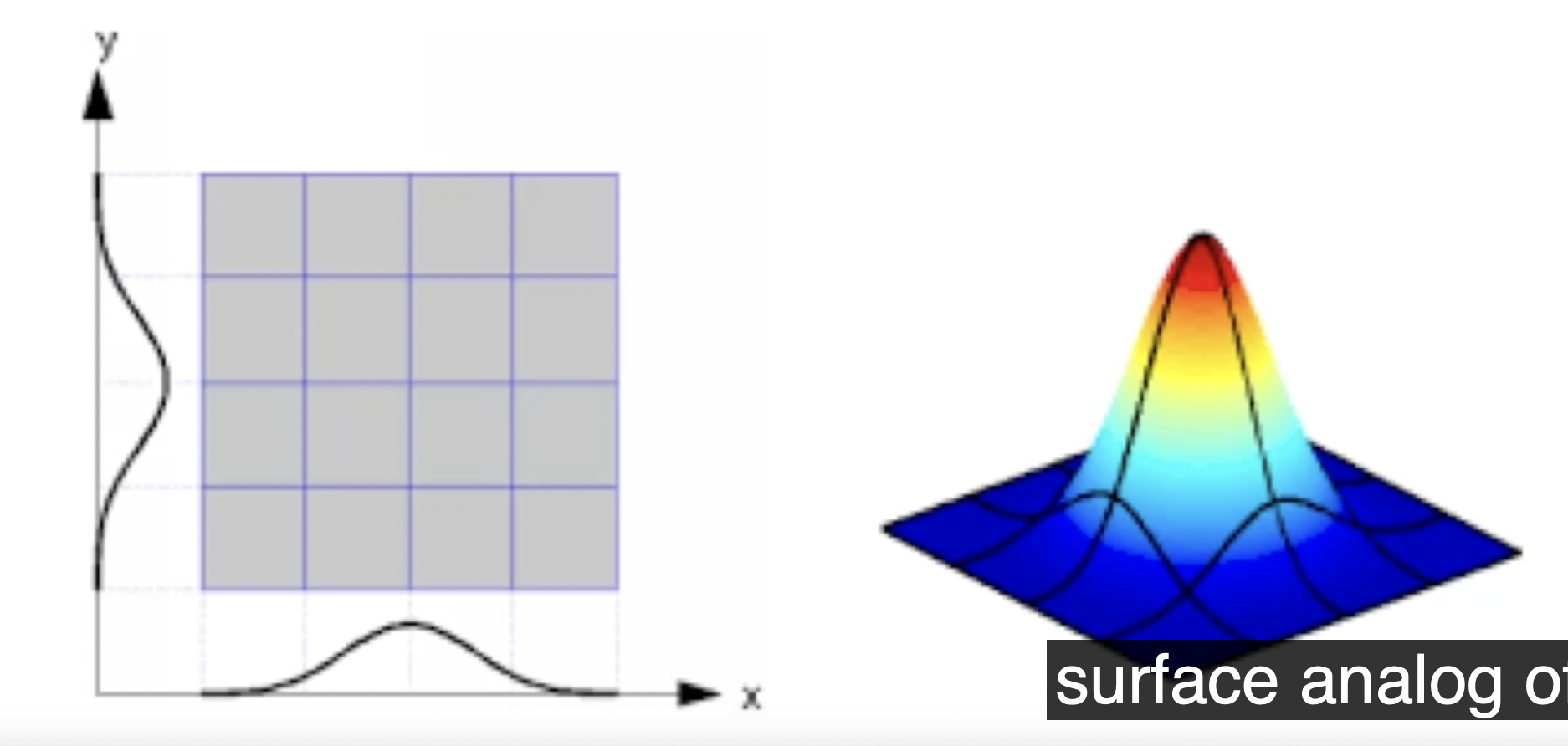
最后, 还有 Implicit Surface: 使用曲面方程的 非显式表示 (Implicit Representation) 描述曲面, 以及 程序曲面 (Procedural Surface): 通过某个描述物体轮廓曲线的周期性运动的轨迹来对曲面 (或物体本身) 建模, 如下图所示.
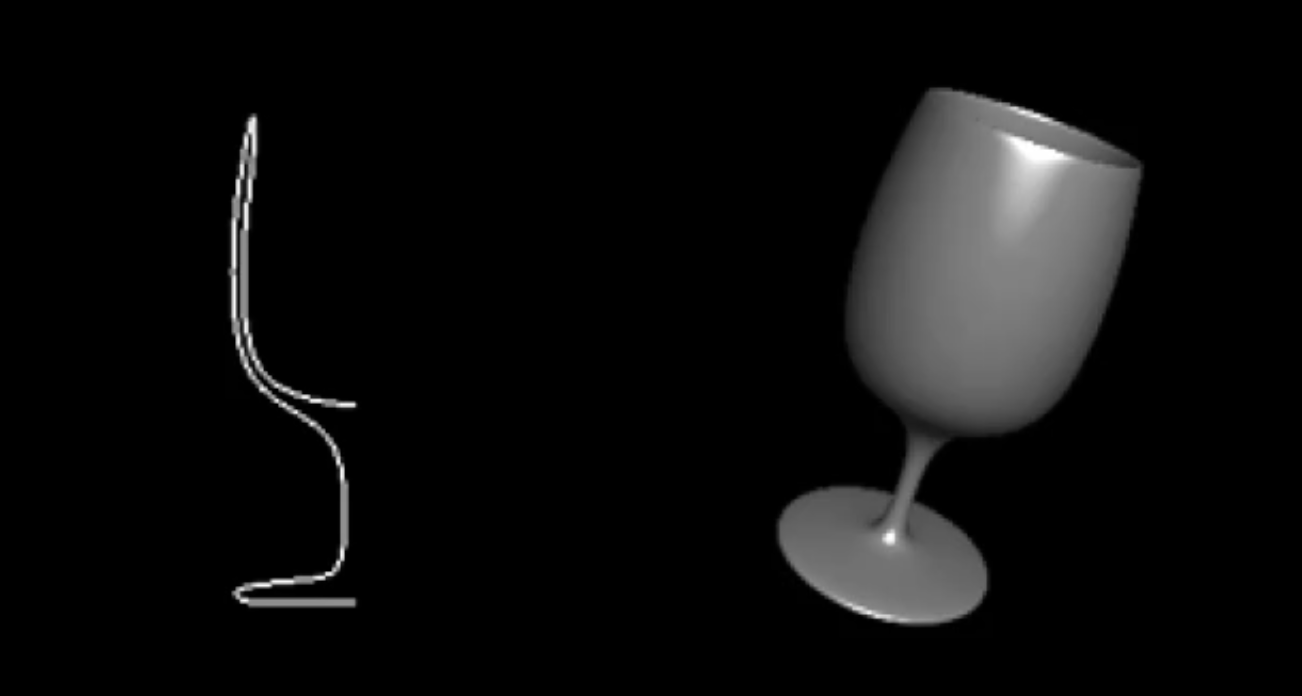
下面讨论对曲面的构造.
曲面的构造方式
在上一节中我们已知, 可以使用包括三次贝塞尔曲线表示法和 B-样条曲线表示法对曲线建模. 曲线在给定 $t$ 的情况下, 其解析式的对应值唯一确定, 因此在将曲线解析式的值和参数 $t$ 的取值视为两个维度的情况下曲线位于二维空间内. 而 其实际上是一维的.
要实现 在三维空间中构造曲面 的目标, 就需要扩充参数, 使解析式所描述的几何物体从 一维曲线 变为 二维曲面.
双三次贝塞尔曲面
还是从贝塞尔曲线开始. 考虑三次贝塞尔曲线, 可知它 有四个控制点. 我们下面用它 建模曲面的一个方向, 方便起见如下图所示考虑竖直方向. 记这些竖直方向的贝塞尔曲线的参数为 $u$.
下面对曲面的水平方向进行建模: 若 假设每个控制点都在另一条不同的, 参数为 $v$ 的贝塞尔曲线上, 则可知得到的是一个 二维曲面: 每个控制点 由参数 $v$ 和 它所在的三次贝塞尔曲线的解析式对应给定参数 $v$ 的值 所确定, 这也就是这些控制点的两个坐标.
而对于任何情况, 给定参数 $v$ 后可以立即确定四个控制点的坐标, 因而可以确定对应水平位置 $v$ 的, 竖直方向上的贝塞尔曲线的解析式; 再给定确定竖直位置的参数 $u$, 就可以得出这个曲面上对应点的坐标, 由此就完成了对三维空间中二维曲面的建模: 该曲面的值完全由两个参数 $u, v$ 决定.
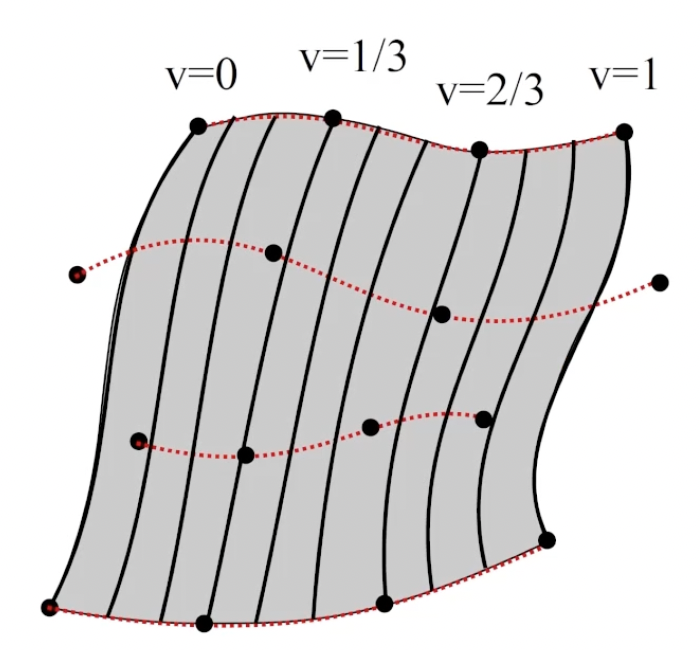
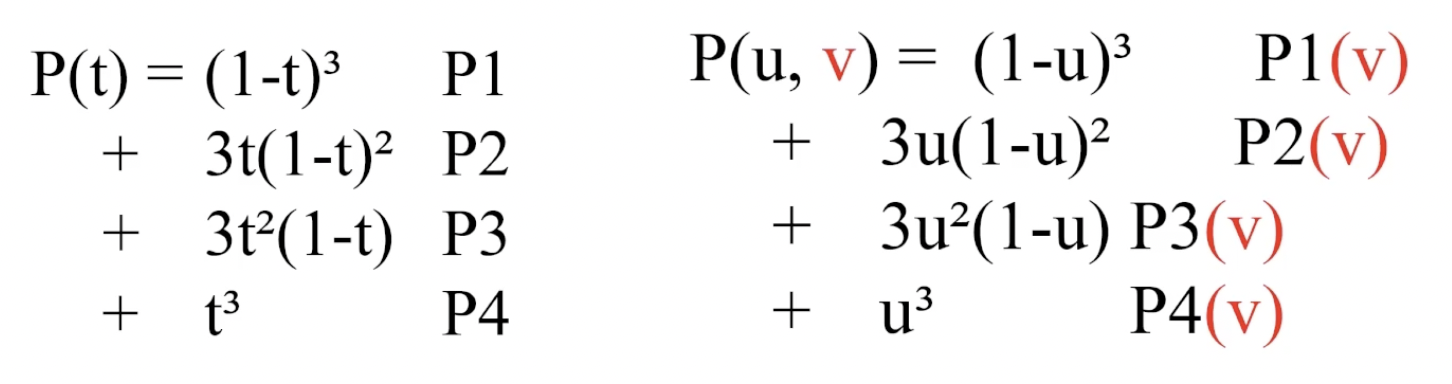
要表示这样的曲面, 就需要 记录全部 $16$ 个控制点. 我们称纯粹由三次贝塞尔曲线表示的曲面为 双三次贝塞尔曲面 (Bicubic Bezier Surface).
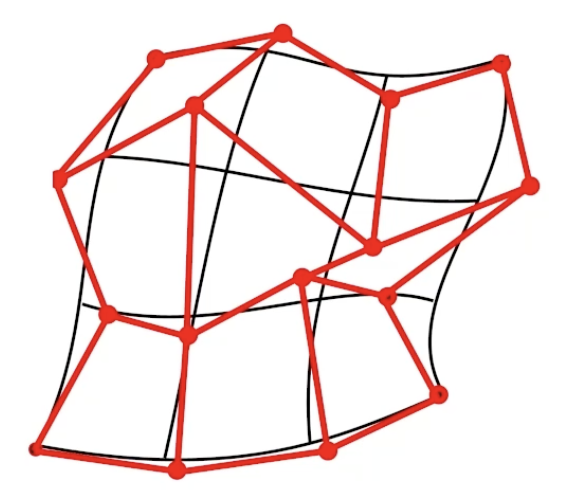
双三次贝塞尔曲面需要 $16$ 个控制点来完全确定.
参数化曲面
下面讨论 参数化曲面 (Parametric Surface):
参数化曲面仍然需要 $16$ 个控制点才能完全描述. 曲面的边缘是对 控制点的近似 (Approximation), 曲面的基是 两个伯恩斯坦多项式的积.
下面考虑曲面上的点. 由于曲面位于 三维空间中, 因此所考虑的点也是 三维的.
在上面的讨论中已经知道, 曲面上的点由参数 $u$ 和 $v$ 唯一确定. 但此处对该点横纵坐标的定义分别为 曲面方程 $P$ 关于 $u$ 和 $v$ 的偏导, 而第三维度则被定义为 曲面在该点的法线向量.
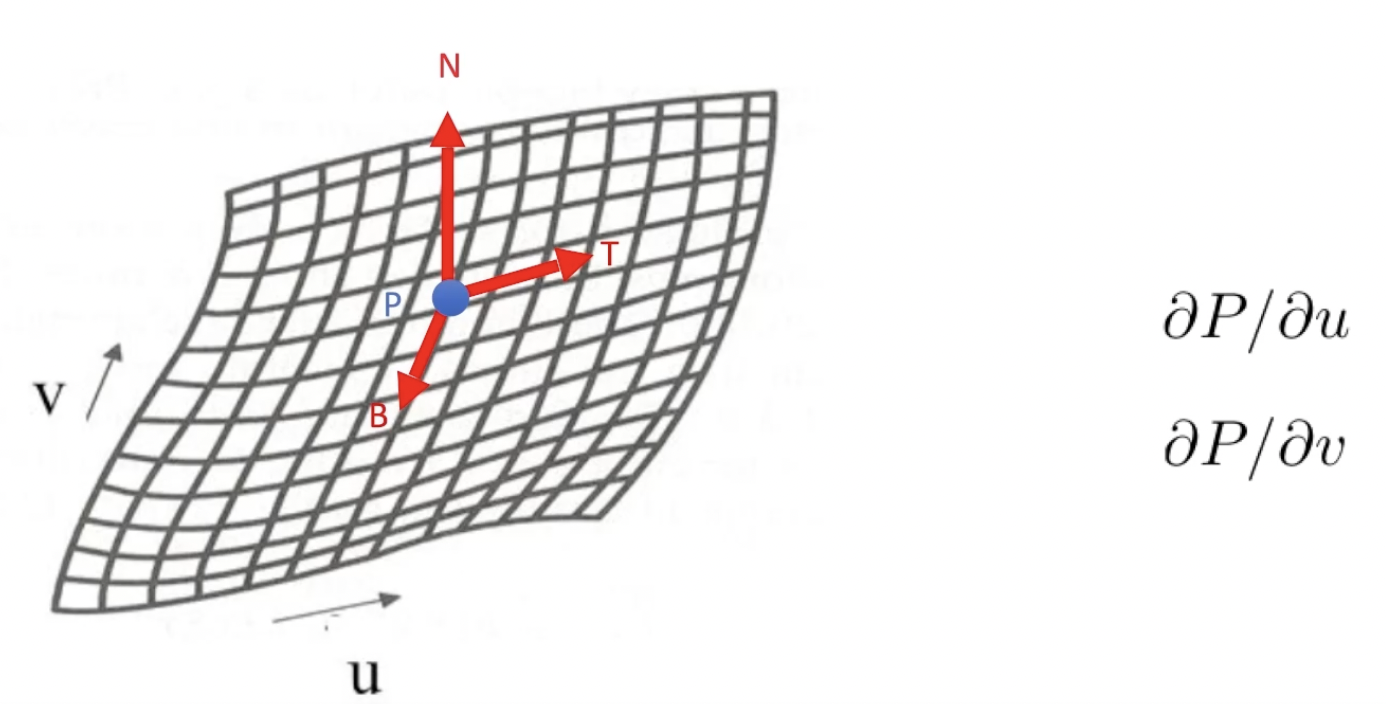
随后讨论参数化曲面表达式的矩阵表示:
我们称参数化曲面为 “Patch”. 基于曲线的矩阵表示, 以及我们前面提到的对曲面的建模思路, 可知:
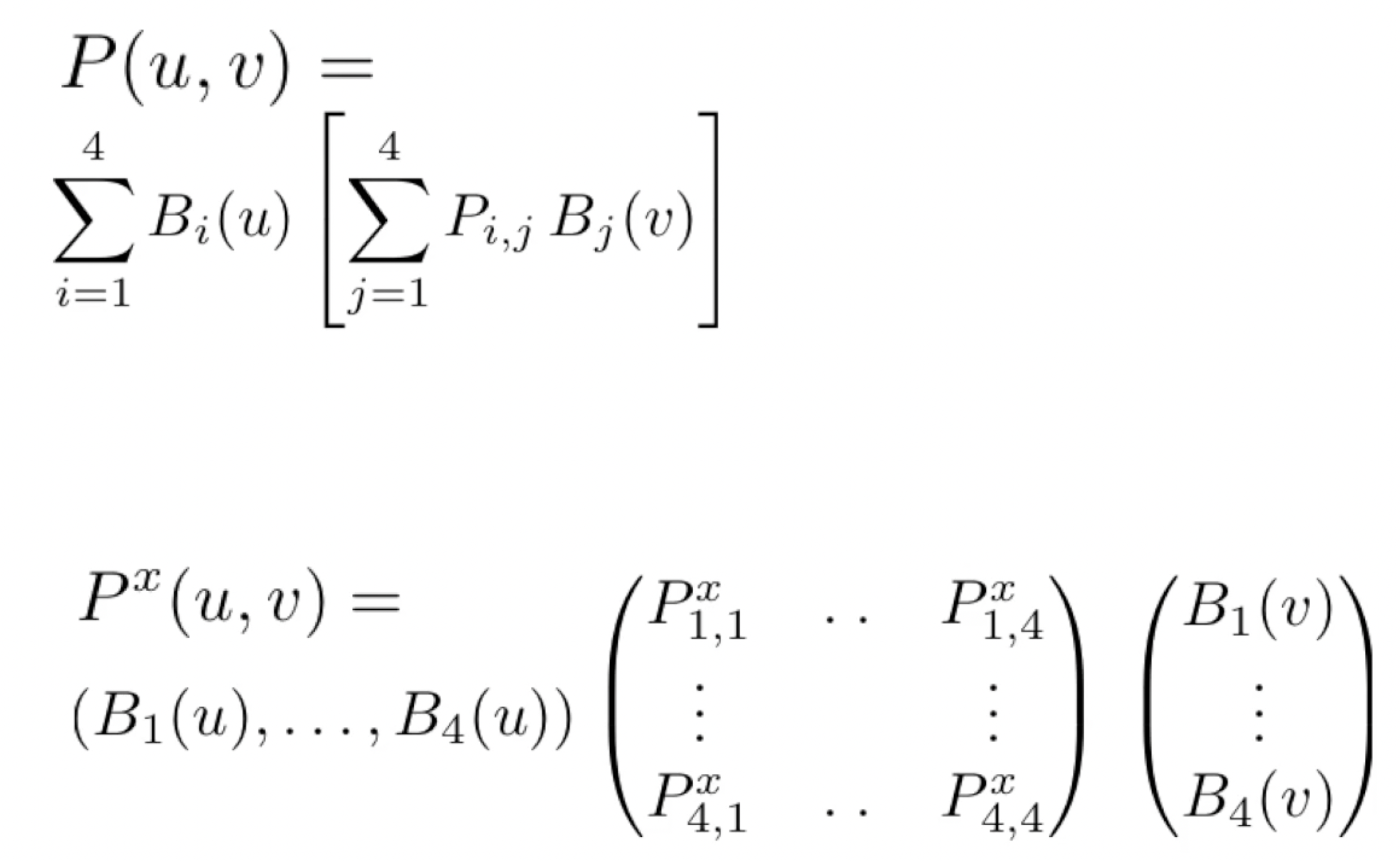
进一步地可写成形式化的矩阵表示:
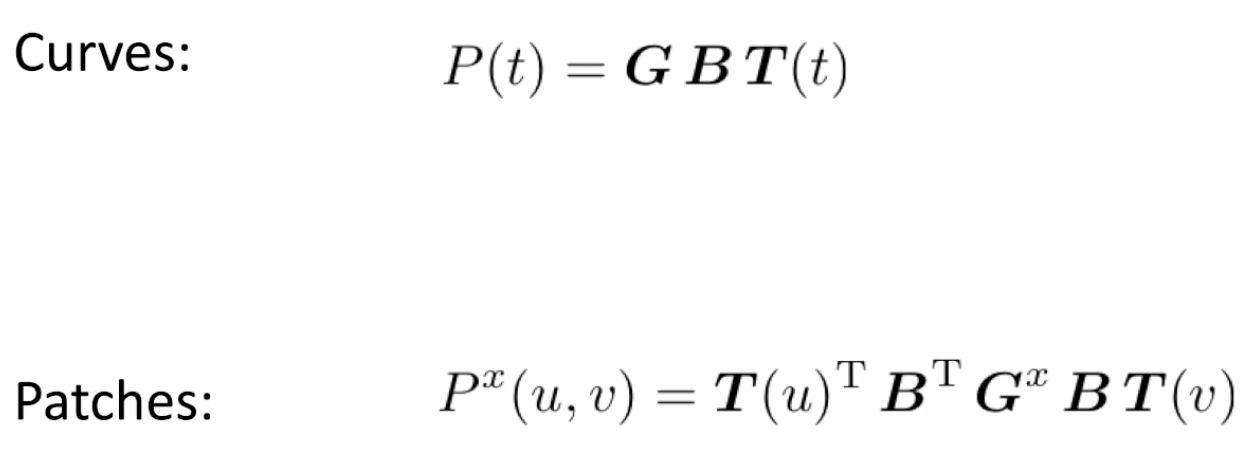
这一表示可用于表示 用B样条曲线或三次贝塞尔曲线 建模的参数化曲面.
参数化曲面可以在仅需 $16$ 个控制点 (这个数量不算多, 但也不算少) 的情况下生成足够平滑的曲面, 但 渲染参数化曲面对计算资源要求高, 因为它在渲染时会被转换为 三角形网格 (Trianglelated Mesh).
此外, 曲面在 Patch Boundry 处的连续性难以保证.
需要注意, 并非所有的曲面都是平滑的. 要建模 非平滑曲面, 我们可以在某个平滑曲面的表面覆盖 Displacement (位移贴图) 将曲面上实际几何点的位置沿着垂直于曲面的曲面法线, 根据存储在贴图对应位置的数值进行移位, 从而产生凹凸不平的纹理.

细分曲面
随后讨论 细分曲面 (Subdivision Surface).
下面讨论最简单的细分曲面技术: 从最初始的多边形网格 (Polygon Mesh) 开始, 对每条边不断进行如 De Casteljau’s algorithm 的 “取中点-链接中点” 的操作, 就可以逐渐得到一条越来越平滑的曲线. 而最终无论如何继续平滑, 得到的曲线仍会被最初始的多边形网格所 约束, 如下图所示:
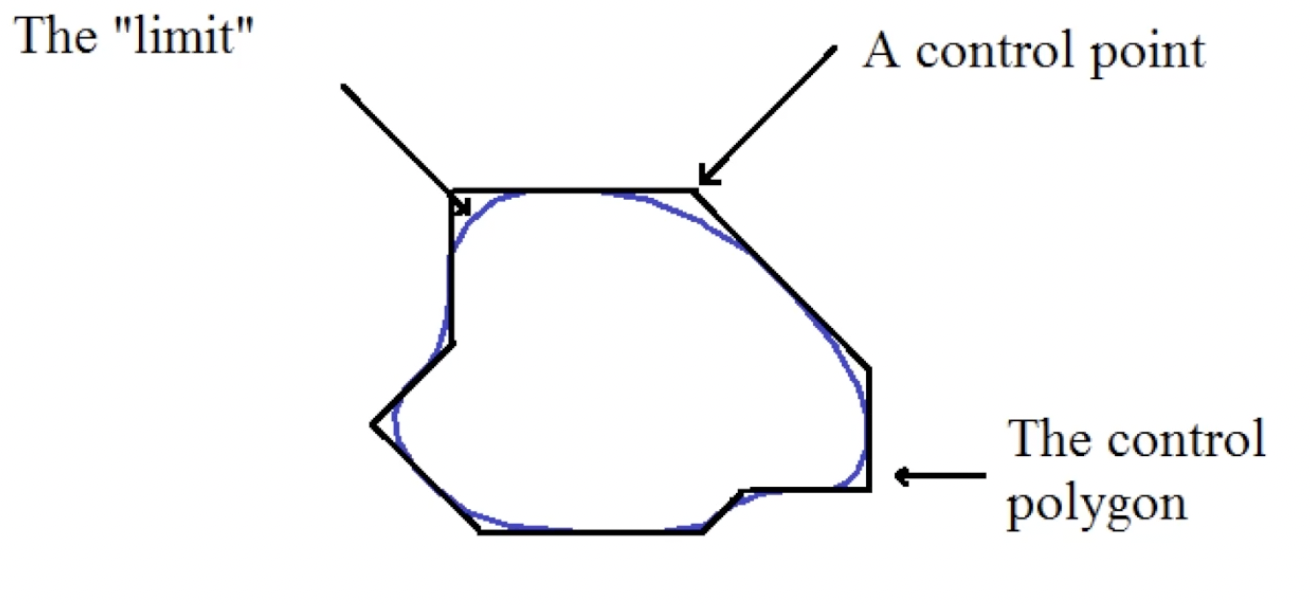
旋转曲面
我们也可以使用特殊构造的曲线生成 旋转曲面 (Surface of Revolution).
典型的旋转曲面表达式可写为:
\[s(u, v) = R(v) \cdot q(u)\]其中 $s(u, v)$ 是曲面的解析式 (或者在 $u, v$ 都确定的时候可以看成是曲面上的一个点), $R(v)$ 是 旋转矩阵, $q(u)$ 是由一系列点组成的向量.
我们还可以通过先构造一段曲线, 然后让曲线沿某条轨迹 (Trajectory) 移动, 取其扫过的曲面作为它所建模的曲面. 该方法称为 General Swept Surface.
这样构造的曲面表达式可写为:
\[s(u, v) = M(c(v))q(u)\]其中 $q(u)$ 就是给定的移动轨迹 它将 提供一个维度, 而 $M(c(v))$ 则是提供第二个维度的, 构成曲面切面的曲线本身.
需要注意, 当移动轨迹是闭合的圆时, General Swept Surface 就是旋转曲面.
标架 Frames
标架 Frame 是用于 完全决定空间坐标系 的, 由三个拥有相同的出发点, 坐标原点 的, 互相垂直的向量 组成, 称为 坐标向量.
一种标架是 Frenet Frame, 它的坐标原点是曲线上 任意确定的点, 坐标向量由 曲线的一, 二和三阶导数 组成, 也就是 切线 (Tangent), 法线 (Normal) 和切线与法线的向量叉乘 (Binormal).
Frenet Frame 的问题是: 由它确定的曲面法线可能会在曲线的某个点之后 方向发生偏转, 称这一现象为 Inflection, 法线方向开始发生偏转的点称为 Inflection Point, 如蓝色箭头所示.
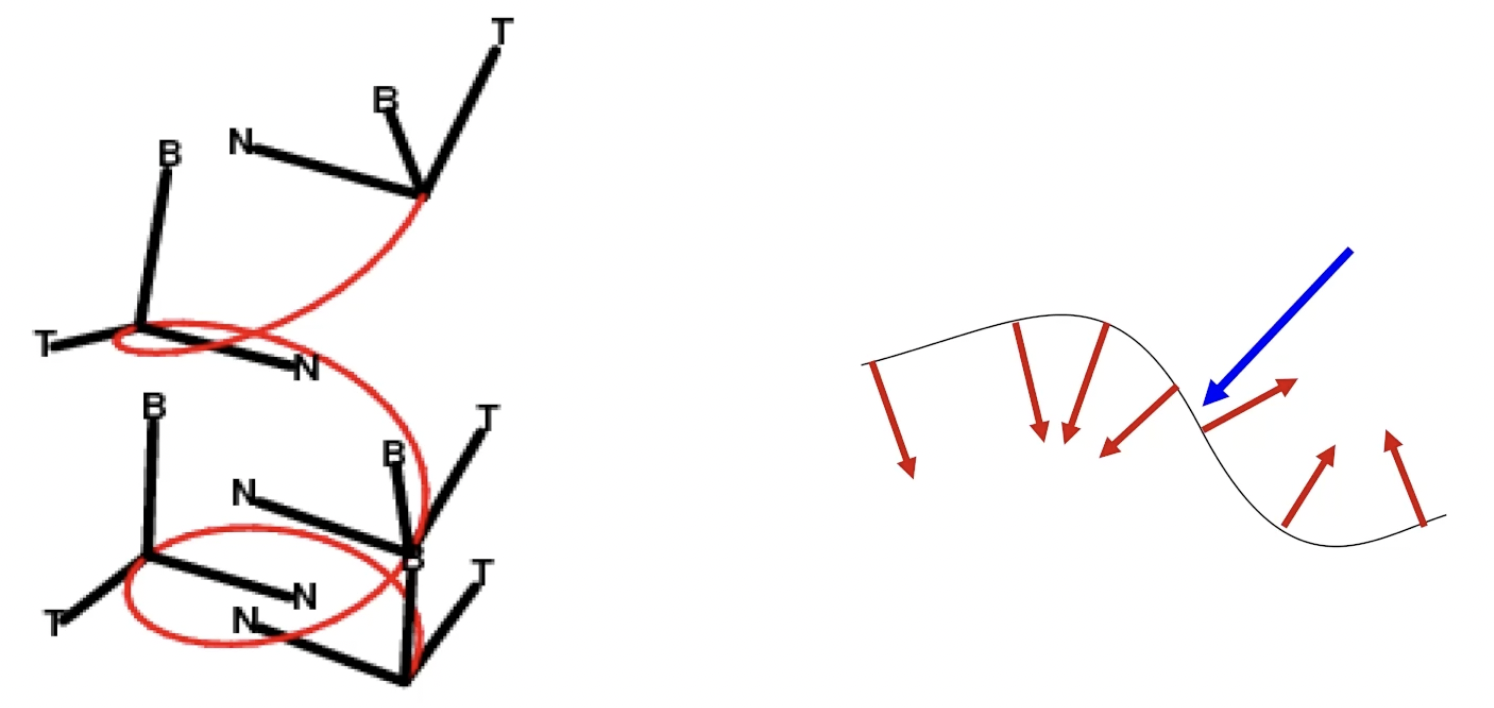
这使我们难以基于曲面法线的方向判定其到底指向 “曲线的内部” 还是 “曲线的外部”, 使它难以用于生成旋转曲面或更一般的 Swept Surface. 因此需要引入对曲线的一种新表示法: 曲线的隐式表示法.
曲线的表示法
我们可以用 隐式表示 对曲面和曲线进行描述. 隐式表示一般指: 曲线或曲面的解析式可以写为 $F(x, y, z, …) = 0$ 的形式.
隐式表示的首要优点是: 通过将点带入解析式, 要判断该点在不在曲线/曲面上, 就只需要检查解析式的值:

也便于进行布尔运算. 其问题是: 每次修改曲线, 任何一个控制点发生变化时都需要重新生成一个隐式表达式.
当然, 我们还可以用 点集 (Point Set) 对曲面或曲线进行描述: 基于给定的一系列 离散 的点, 对这些点进行 近似, 生成曲线或曲面. 这一表示法非常适合扫描仪对物体进行 3D 扫描得到的点集数据. 同时, 我们可以直接向点集中 添加或删去某个或某些点 实现对曲线或曲面的修改.

当下主流的, 对曲线/面的表示方式是: 结合隐式表示和点集表示.
最后对三种主流的曲面表示方法的优劣区分总结如下:
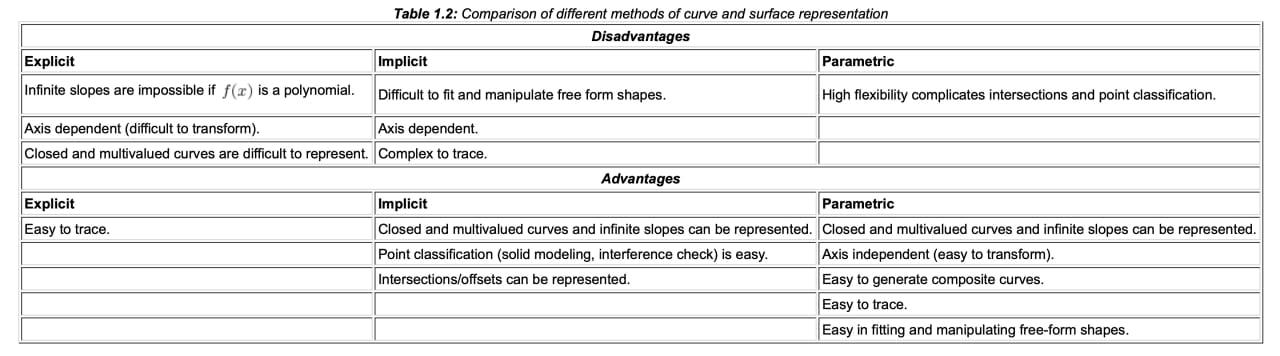
Explicit和Implicit都是Axis Dependent的.Explicit和Parametric都是Easy to trace points的.Closed and multivalued curves都可在Implicit和Parametric曲面表示中轻松表达, 而Explicit不行.Parametric不适用于需要大量拼接曲面或检测点在曲面上/外/内的场合.Implicit自然适用于点位置的检测.
