图论算法初步
!!注: 完整详细的复习内容请参阅 《COMP36111 期末总复习》.
在本章中, 我们将介绍一系列图论相关的基本概念, 并介绍数个图论相关算法.
1. 有向图的基本概念
首先回顾与图论相关的一系列基本概念:
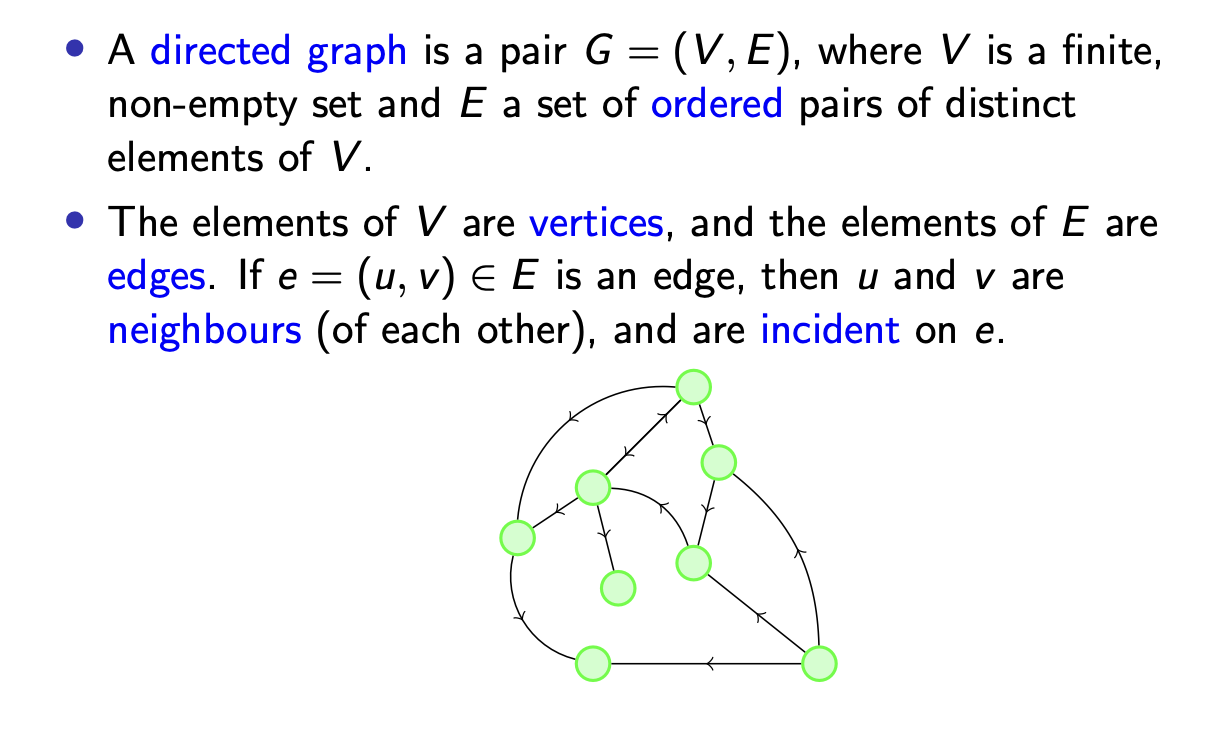
定义 1.1 (Directed Graph 有向图)
有向图 由 顶点集 $V$ 和 边集 $E$ 组成, 记为 $(V, E)$.
定义 1.2 (Edges 边)
有向图的 边 由两个顶点组成. 若记这两个顶点为 $u, v$, 则这条边可记为 ${u, v}$ 或 $(u, v)$. 注意这是对有向图的表示, 因此该表示同时说明: 这是一条从 $u$ 指向 $v$ 的边.
定义 1.3 (Neighbor 邻居)
若边 $e = (u, v)$ 在图 $G$ 中, 称 $u$ 和 $v$ 为邻居.
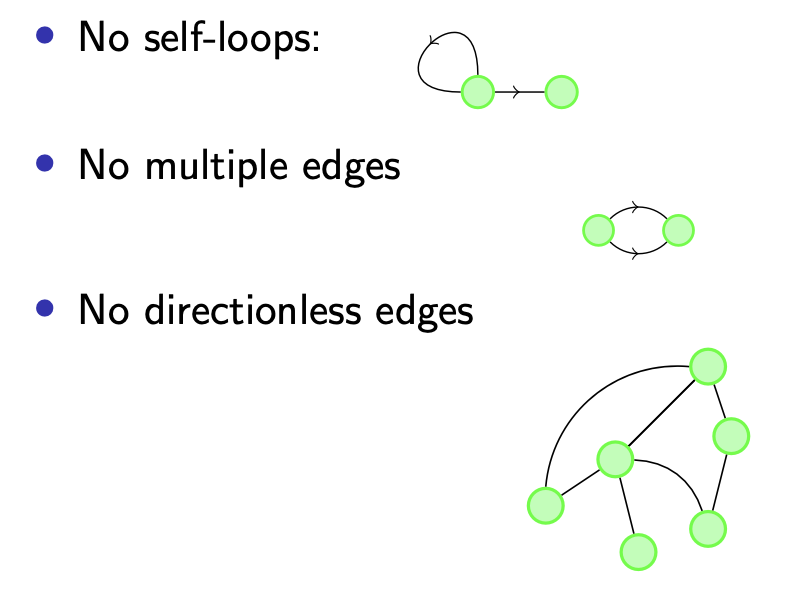
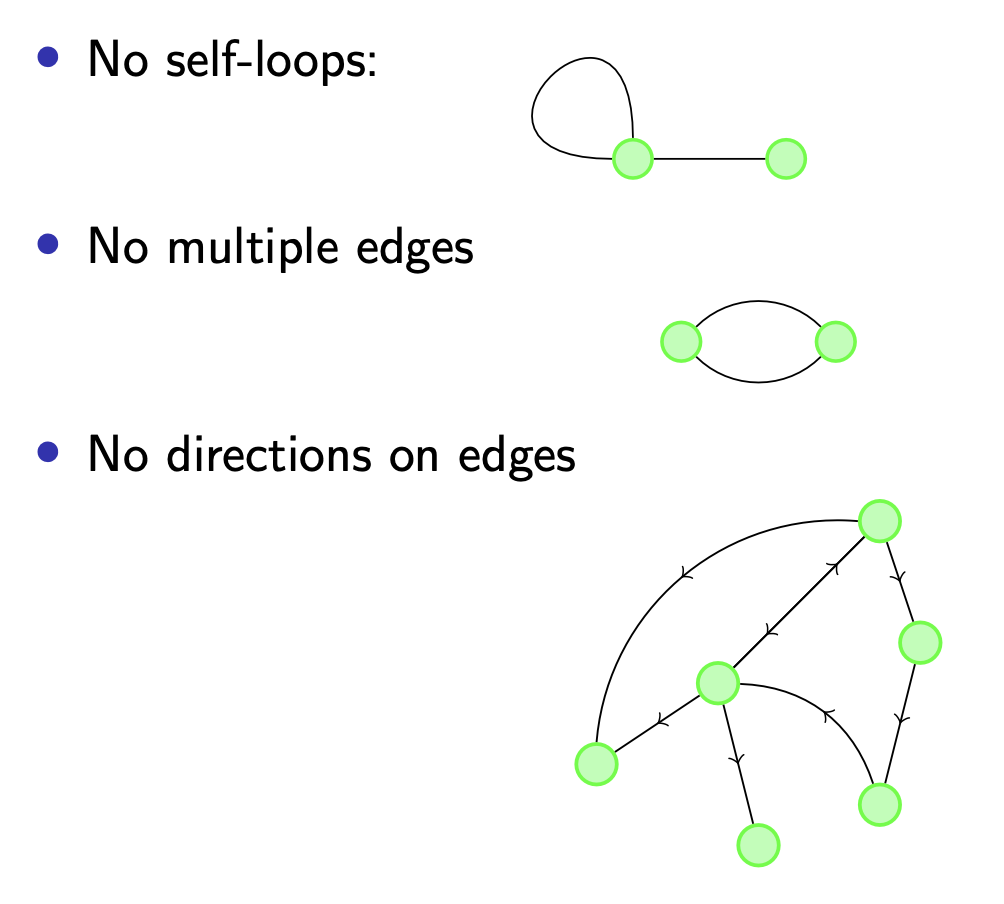
需要注意, 在 有向图 中 不存在从某个顶点指向自身的边, 也不存在 起点和终点重合的边, 更不存在 没有方向 的边.
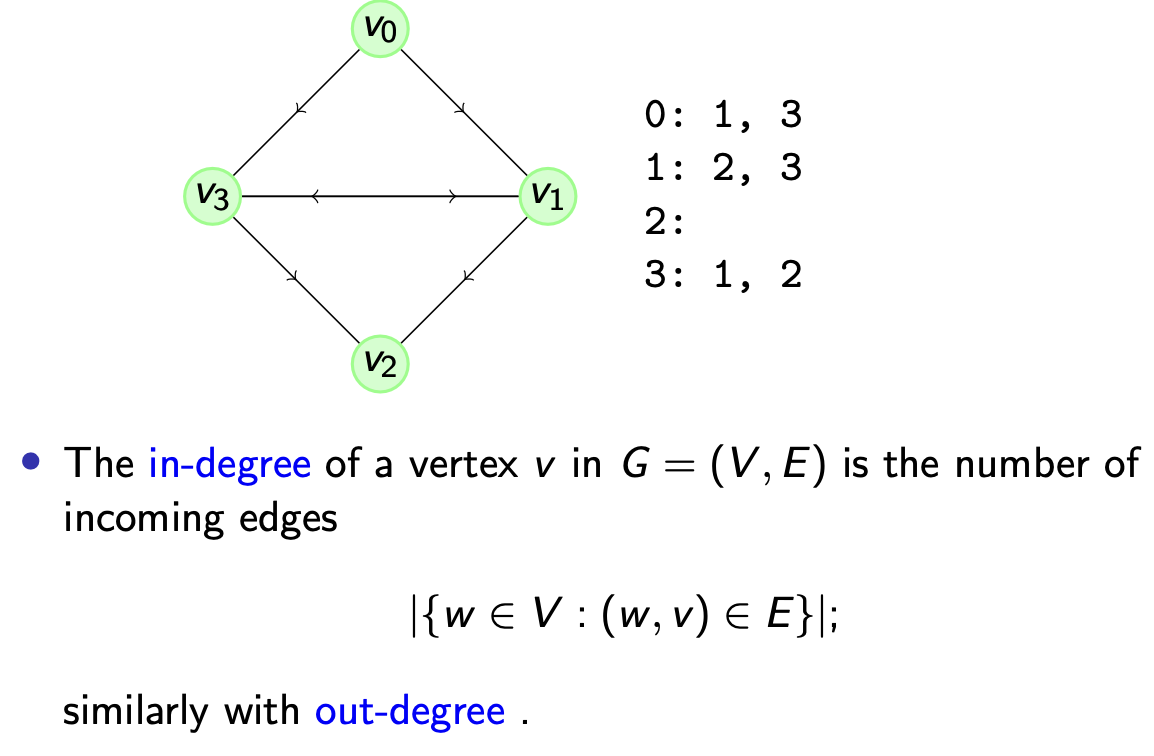
定义 1.4 (In | Out degree 有向图的入度和出度)
考虑图中的任意顶点 $v$, 称图中 以 $v$ 为目标顶点的边的数量 为该顶点的 入度, 而 以 $v$ 为起始顶点的边的数量 为它的 出度.
定义 1.5 (Path 路径)
称图 $G$ 中的 路径 为一系列 不同的顶点 $v_0, \cdots, v_k$ 组成的序列, 其中 $(v_0, v_1), \cdots, (v_{k-1}, v_k)$ 等 都是图 $G$ 中的边.
换言之, 路径就是图中一系列依次首尾相连的边的顶点依次组成的序列.
定义 1.6 (Reachability 可达性)
考虑图 $G$ 中的一对顶点 $s, t$, 称 从 $s$ 到 $t$ 是可达的, 若在图中存在一条 从 $s$ 到 $t$ 的路径.
定义 1.7 (Strongly Connected 强连通)
称某个有向图是 强连通 的, 若它的 任意一对顶点 都是 互相可达 的.

在了解了上述概念后, 我们不难关于有向图提出下列的两个问题:
-
st-CON:`给定某个有向图 $(V, E)$ 和图中的两个顶点 $s, t \in V$, 确定从 $s$ 到 $t$ 是否是 可达的. 它可以通过深度优先算法解决.
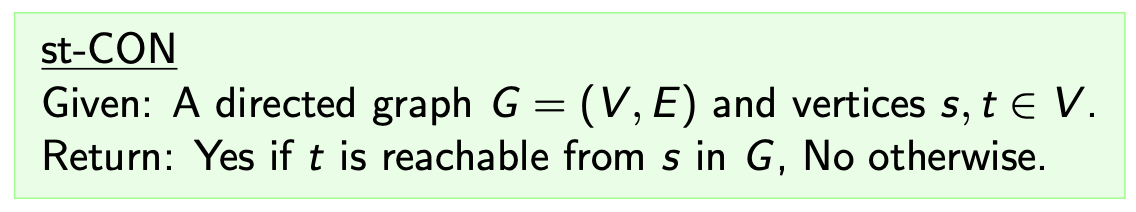
-
STRONG CONNECTIVITY:给定某个有向图 $(V, E)$, 确定它是否是强连通的.
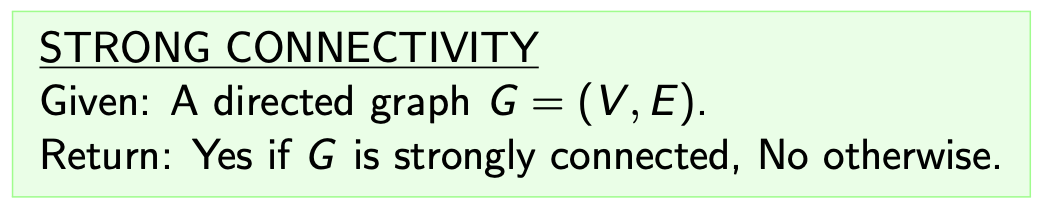
2. 拓扑排序
下面我们讨论 拓扑排序.
首先需要继续定义图中 环 的概念:
定义 2.1 (Cycle 环)
称有向图 $G$ 中的 环 为一个 首尾相连的路径. 即:
该路径可被表示为 $v_0, \cdots, v_k, ~~ k \geqslant 1$ 的形式, 且 $(v_k, v_0)$ 同样为一条边.
若图 $G$ 中存在 至少一个环, 则称其是 有环图 (
Cyclic), 反之称其为 无环图 (Acyclic).
自然地我们想要解决下列的问题:
给定一个 有向图 $G$, 确定它是 有环的 还是 无环的.
结合第一节中介绍的定义 度, 不难得出下面的引理:
引理 2.1
若有向图 $G$ 是 无环 的, 则在图中 必存在某个入度为 $0$ 的顶点.
证明: 不难考虑有向图的对立: 树. 显然树的 根节点 就是入度为 $0$ 的. $\blacksquare$
下面引入 拓扑排序 的定义:
定义 2.2 (Topological Sort 拓扑排序)
称 拓扑排序 为某个 有向图 $G$ 上 对它顶点的排序
\[u_0, \cdots, u_{n-1}\]使得对任何边
\[(u_i, u_j)\]都有 $i < j$.
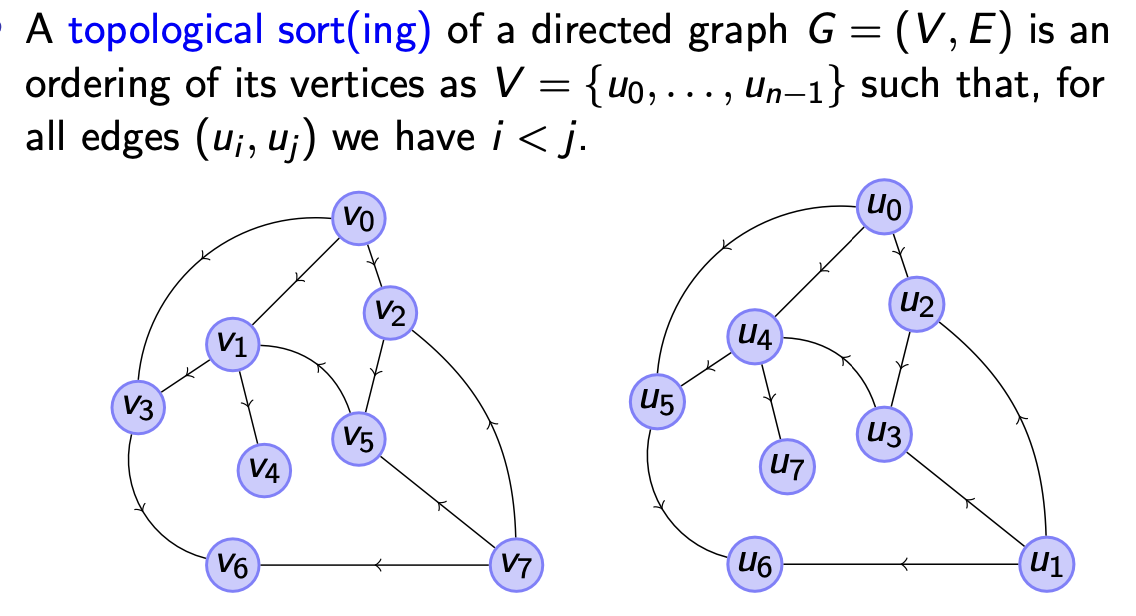
我们可将拓扑排序定义为下列的算法问题:

可知: 任何有环图都不存在拓扑排序, 且任何无环图都必有一个拓扑排序.
拓扑排序的伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def topSort(G):
# 计算图中每个顶点的入度
G.inDeg = handleIndegreeComputation(G)
# 栈 S 用于存储所有已发现但尚未使用深度优先遍历到的顶点
S = []
# i 在此处作为索引
i = 0
# sort 存储拓扑排序的最终结果
sort = [None for _ in range(len(G.vertices))]
# 使用深度优先搜索, 首先考虑所有起始点 (即入度为 0 的点)
for v in G.vertices:
if G.inDeg(v) == 0: S.push(v)
while len(S) != 0:
# 依次考虑栈首的点 (深度优先)
v = S.pop()
sort[i] = v
i += 1
# 遍历点 v 的每一个子节点, 在子节点的入度为 0 时再去遍历它, 确保排序的顺序性
for w in G.edges(v):
G.inDeg(w) -= 1
if G.inDeg(w) == 0:
S.push(w)
# 在全部遍历后, 若所有节点的入度都可变为 0 则说明该图是无环的
if i == n:
return sort
else:
return "Impossible"
下面对拓扑排序的正确性给出证明:
- 可以看出, 在任何一个顶点被从栈中弹出时, 它的所有前置节点必然已被弹出, 因此它们必然有更低的编号.
- 若所有的顶点都被赋予某个编号, 则可确定我们必对这个有向图达成了拓扑排序.
- 若某个顶点在最后被除去了编号, 则说明被检测的有向图 $G$ 必有一个 有向子图 $G’$, 其中 每个顶点的入度都不为 $0$. 因此可知 $G‘$ 和 $G$ 都是有环图.
- 由此可知, 在此情况下对 $G$ 而言不存在拓扑排序. $\blacksquare$
同时基于伪代码可知: 拓扑排序的时间复杂度是:
\[O(\vert V \vert + \vert E \vert).\]因此可知, 我们可以将 “给定的有向图是否为有环图” 的问题转换为 “该图是否具备拓扑排序” 的问题. 由于拓扑排序算法的时间复杂度是线性的, 因此我们可以使用拓扑排序 在线性时间复杂度内 解决 有向图的有环/无环问题.
3. 有向图中的强连通分量问题
在介绍 Kosaraju 算法前首先需要对图的 强连通性 给出定义.
定义 3.1 (Strongly Connected Component 强连通分量)
记有向图 $G= (V, E)$, 称 $G$ 的 强连通分量 为: $G$ 的最大强连通子图的顶点集.
也就是说: $G$ 的强连通分量就是它顶点集 $V$ 的一个子集 $V’$, 它是 全连通 的, 其中任何一对顶点在 $G$ 中都在 有向图 的意义下可达 (也就是相互之间可达), 而且如果向 $V’$ 中加入任何一个新的顶点都会破坏这个子集的全连通性.
比如考虑下面的例子:
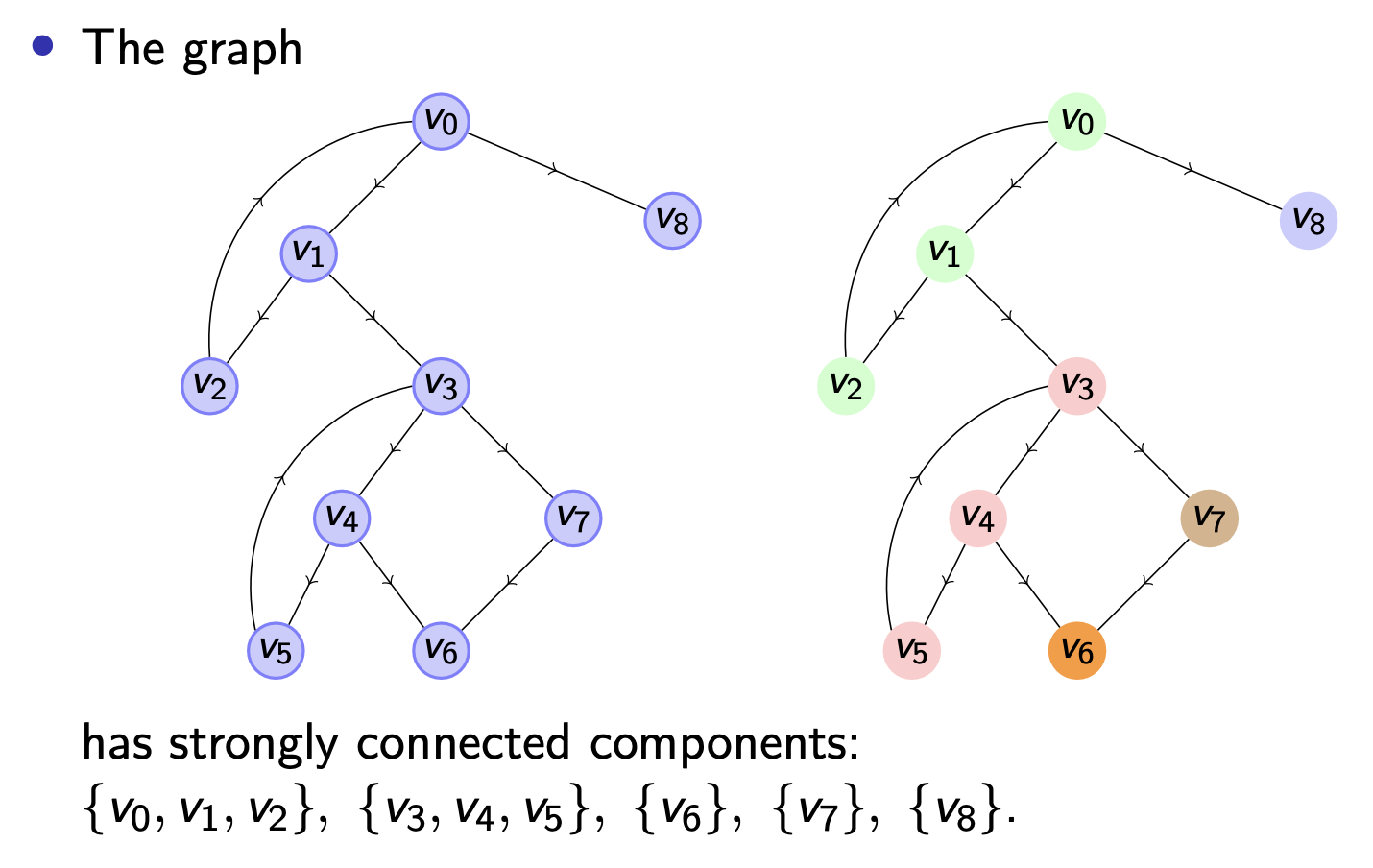
因此我们自然提出了下面的问题: 如何寻找某个有向图的 所有强连通分量?

首先给出结论: 有向图的所有强连通分量可以在线性时间中找到. 其次给出两个算法: Tarjan 算法和 Kosaraju 算法.
Kosaraju 算法
Kosaraju 算法的基本思路是:
-
首先对给定有向图的 任意一个点 开始进行深度优先遍历, 然后依次将 完成遍历的节点存入某个栈中. 注意此处在遍历到每个节点时都会 先将这个点标记为 “visited”, 若该点的所有子节点都是 “visited”才算作完成遍历, 因此 被存入栈中的节点必属于某个强连通分量. 这一步 实际上完成的是对原图 $G$ 的反图 $H$ 的伪拓扑排序 $S$.
(为什么是 “伪拓扑排序”? 因为真正的拓扑排序在 有环图 上必不存在, 而任何强连通分量都必然是有环的. 所以这里的 “伪拓扑排序” 到底是什么? 它就是 将原来的强连通分量中环随机切掉一条边之后得到的无环图的拓扑排序.)
(为什么这条边是随机切掉的? 因为我们开始遍历时选择顶点的顺序是 随机 的. 因此在遍历强连通分量时, 最后遍历到的边也不是确定的. 根据算法逻辑可知, 切掉的边必然是 最后一个点到最初一个点之间连成的边.)
- 由拓扑排序的定义可知, 它实际上已经将原图中所有的强连通分量归类排好序了 (考虑任意两个顶点 $v_i$, $v_j$, 可知要么有一条边 $(v_i, v_j)$, 也就是说它们同在一个强连通分量重, 要么这两个点互不隶属).
- 由于对图的边取反 不会影响原来图中强连通分量之间的连通性, 而 原本不连通的分量之间在取反后还是不连通, 因此只需要对取反的图根据拓扑排序 $S$ 再执行一次深度优先搜索,就可以依次找出所有的强连通分量.

其中

其代码如下:
1
Tarjan 算法
Tarjan 算法是另一种基于深度优先搜索, 但 只需搜索一次 的算法:

4. 无向图的基本概念
下面讨论 无向图.
定义 4.1 (Undirected Graph 有向图)
无向图 由 顶点集 $V$ 和 边集 $E$ 组成, 记为 $(V, E)$.
定义 4.2 (Edges 边)
无向图的 边 由两个顶点组成. 若记这两个顶点为 $u, v$, 则这条边可记为 ${u, v}$, $(u, v)$ 或 ${v, u}$, $(v, u)$.
定义 4.3 (Neighbor 邻居)
若边 $e = (u, v)$ 在图 $G$ 中, 称 $u$ 和 $v$ 为邻居.
定义 4.4 (Adjacent 邻接)
若点 $v$ 在边 $e$ 中, 边 $e$ 属于图 $G$ 的边集, 则称 $v$ 和 $e$ 是 邻接 的.
同样, 无向图中也不存在 从某个顶点到自己的边, 不存在重复的边, 每一条边都不存在顺序.
5. 无向图的连通分量问题
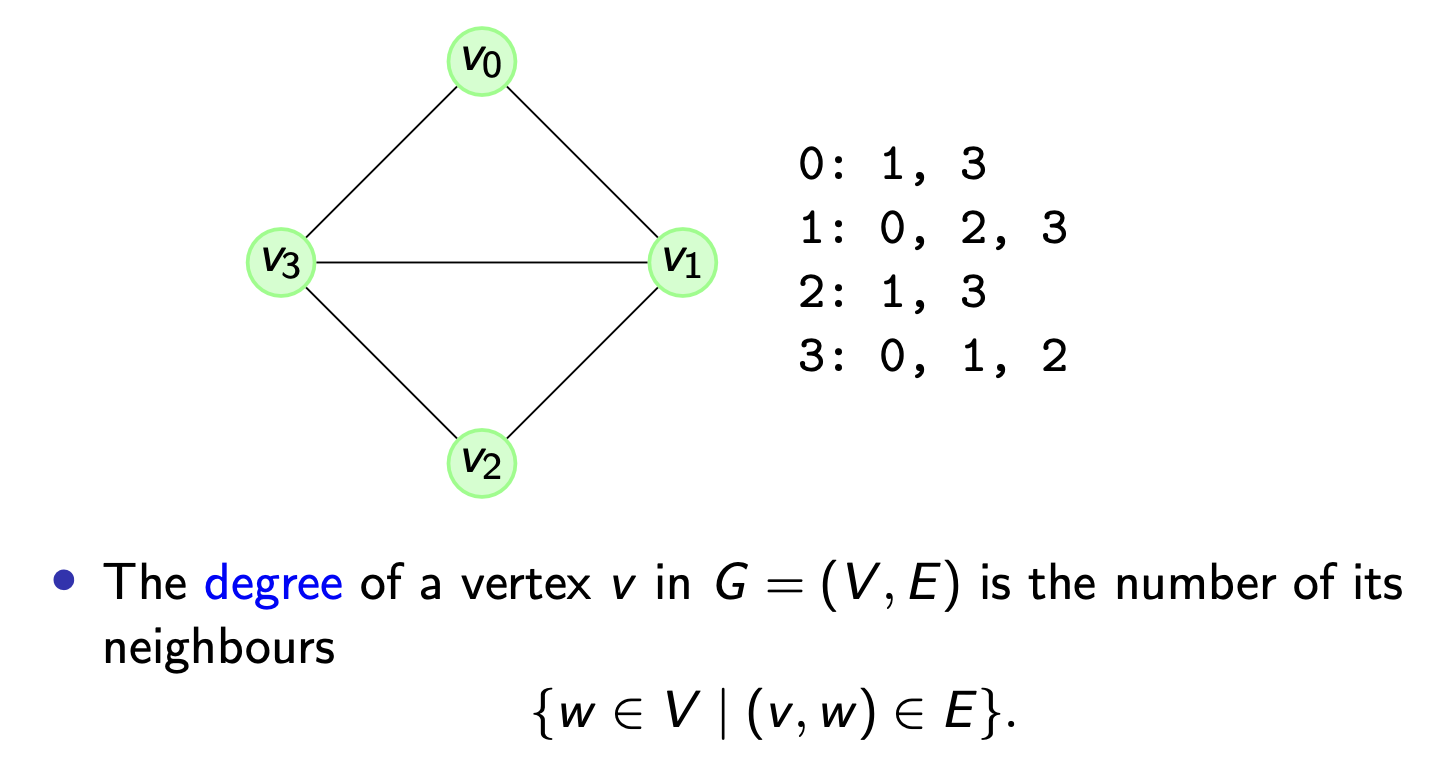
由于无向图的边 没有顺序, 因此它只有 度 (Degree) 的概念:
定义 4.5 (Degree 无向图的度)
考虑图中的任意顶点 $v$, 称图中 包含 $v$ 的边的数量 为该顶点的 度.
同样地, 我们可类似地定义无向图中 路径, 可达性 和 连通性 的概念:

相应地, 我们同样要在无向图中考虑 可达 和 连通 的问题.

进一步地, 我们更关注 如何找出 给定无向图中 连通分量 的问题:

下图所示的图包括三个连通分量.
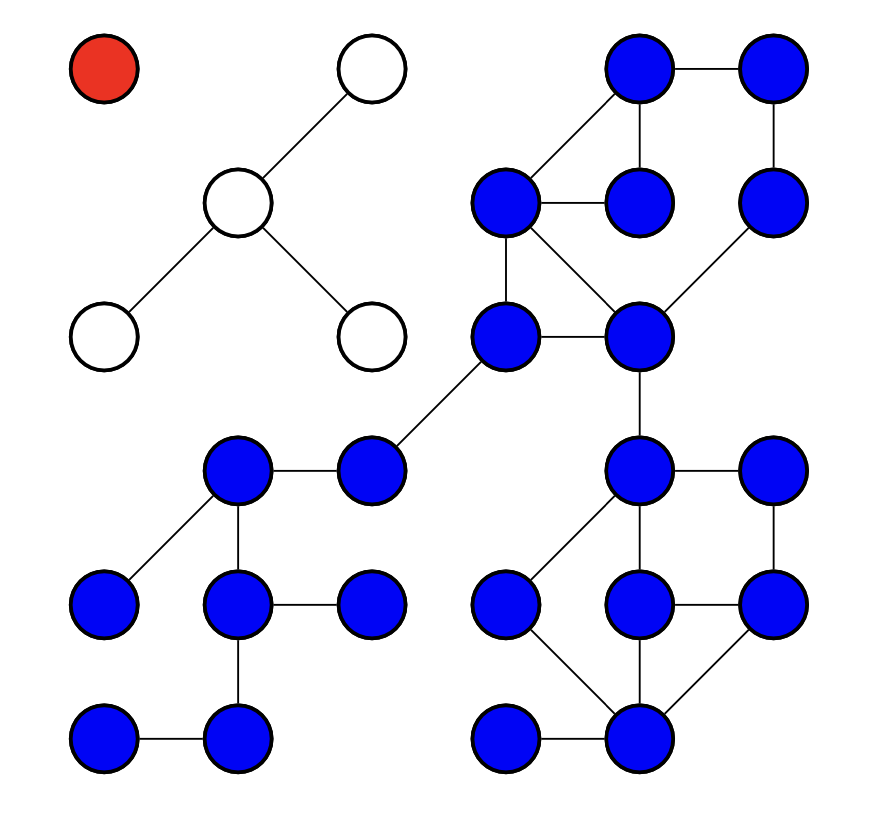
首先不难看出, 无向图的连通分量问题可以用 深度优先搜索 在 线性时间复杂度 下解决:

而我们可以用 Union-Find 结构 (也就是并查集) 更高效地解决无向图的连通分量问题.
6. Union-Find 结构
在正式介绍 Union-Find 结构前, 首先需要引入 对图的分划 的概念.
定义 5.1 (Partition 图的分划)
称对图 $G$ 的顶点集 $V$ 任一个 不包含空集的, 互不相交的拆分 为对这个图的 分划.
同时称图的分划中 任一个元素 为
Cell.
在对无向图 $G$ 进行分划后, 就可以对它进行下列的操作:

其中:
1
2
3
4
5
6
7
8
9
10
11
12
13
def makeSet(v):
s = [v]
v.cell = s
P.add(s)
def find(v):
return v.cell
def union(s, t):
P.remove(t)
s = append(s, t) # this operation will also update p
for v in t:
v.cell = s
注意这是最原始的版本, union 方法的运行时间复杂度至少是二次方级别的, 因为需要将 $t$ 中所有的元素都连到 $s$ 上.
结合上述对图的分划可进行的三种操作, 就可以使用 Union-Find (并查集算法) 解决无向图的连通分量问题:

不难看出, 其基本思想是: 初始状态下将每个顶点视为一个单独的 Cell, 然后遍历每一条边, 将同一条边上的两个顶点所属的 Cell 合并. 因此程序执行各种操作的次数共为 $\vert V \vert + \vert E \vert$.
为了减少运行时间复杂度, 我们可以在构造 Cell 时 记录每个 Cell 的大小, 由此在合并两个不同 Cell 的时候就可以将 更小的连接到更大的 Cell 上.

此外有以下结论:

以及

在此基础上, 还可以应用 Path Compression: 在访问到 Cell 中的每个元素时, 都将它 直接连接到这个 Cell 的代表元上.


