博弈论导论
从本章开始我们正式进入 博弈论 的学习.
基本定义
直观的说, 在任何情况下, 一系列个体 (Agent) 之间进行 交互, 并共同对交互的结构产生了影响, 则称这样的交互为 博弈. 我们有下面的例子:

而在上述的例子中, 我们可以抽象出 博弈 应该具备的 一般要素:
- 有一系列 互相交互 (
Interact) 的个体 (Agent). 称这些个体为博弈中的 决策主体 (Player). - 在任何一次交互后, 所产生的 结果 必须是 可用数值描述 的: 每个决策主体都会相应得到对应的 回报 (
Pay-off), 它可能是 负的. - 这些交互存在明确的 规则, 决定每个决策主体在任何情况下可以进行那些决策. 而在所有决策主体都进行了这样的一系列决策后, 最终交互必然会产生一个 可被规则唯一描述 的 结果 (
Outcome).
博弈的扩展式表述
基于交互的性质和交互的规则可知, 在任何时刻, 任何决策主体可进行的决策类别和对应的决策结果都是确定的. 因此, 进一步地可知, 满足上述描述的 三个一般要素 的博弈过程可以被表示为 决策树. 这也被称为 博弈的扩展式表述 (Extensive form Representation).
在博弈的扩展式表述中, 决策树的每个节点表示一个 决策点, 而边就是决策点间的连接, 表示 某个决策主体进行的, 导致状态发生转换的一个决策, 可以类比为棋类游戏中的 “走棋”. (Move)
同时可知, 显然决策树的根节点就是一切决策的开端,
进一步地, 决策树中 不存在环. 因此任何用决策树表示的决策过程都可以被表示为 自顶向下 的, 清晰明确的决策过程.
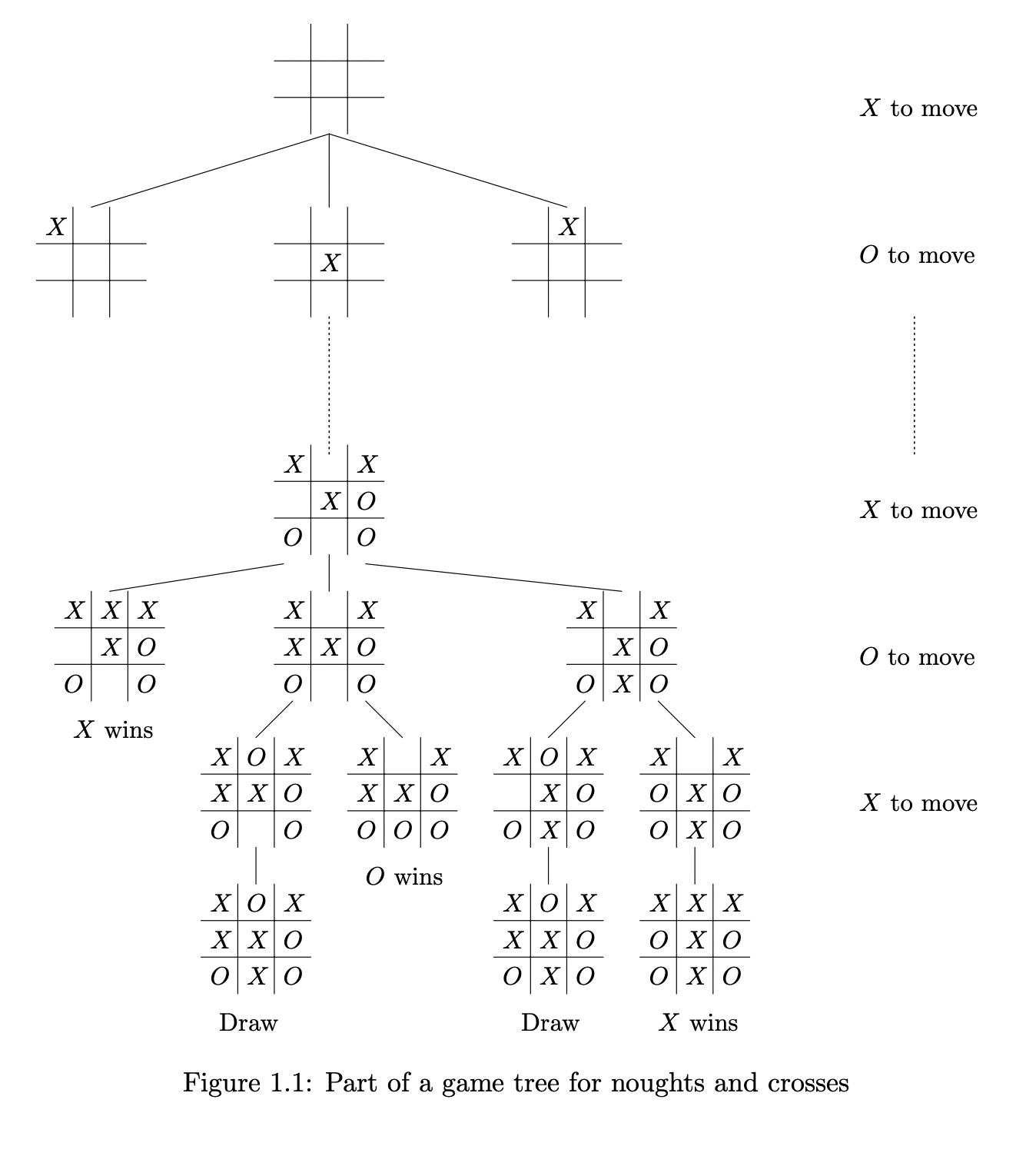
如上图所示, 在使用扩展式表述描述博弈过程时, 在每个节点都需要 明确当前的博弈状态, 以及在每一层都需要明确描述 当前执行决策的博弈主体是谁.
同时, 在对 Pay-off 进行建模时, 并不一定需要将其 建模成某个数值本身 , 使用 由数字组成的元组 也是极为常见的建模方式. 扩展式表述的叶子结点代表着博弈的终结, 此时每个博弈主体都会被赋予对应的 回报.
在博弈的扩展式描述中, 任何一条从决策树的根节点到某个叶子节点的 路径 都可被视为时一个 博弈实例 (A play of the game). 同时可知, 任何节点都唯一地确定了某个博弈实例. 换言之, 每个节点都包含了这样的一部分信息: 只有在它之前执行特定的一系列决策, 才可能从根节点到达它. 我们将在后文中详细讨论这种建模方式的利弊.
同样地, 每个节点也都可视为某个 子博弈实例 的根节点.
基于上述定义的 决策的扩展式表述 具备相当的局限性. 它在未经修正的情况下无法表示下列的情形:
-
玩家做出的决策受一定的概率因素影响的情形: 在某些情形下, 玩家做出的决策到底是什么取决于概率因素的影响, 比如在飞行棋中掷骰子决定步数, 或在卡牌游戏中抽卡等. 这样的决策不是完全由决策主体决定的.
-
数个玩家同时做出决策的情形. 该情形的解决方式和第三点相同.
-
玩家在做出决策时并未掌握完充分信息的情形. 如卡牌游戏中一样, 玩家在做出决策时可能并无法掌握当前局面的所有信息.
下面我们依次讨论第一点和第三点, 第二点在讨论第三点的时候就可被一并解决.
处理存在不确定性的情形
为了处理 不确定性, 我们需要 引入一个新的决策主体 用来模拟现实中的不确定性, 称为 自然主体 (Nature). 和常规的决策主体不同, 自然主体在决策结束时 不被计算回报, 而在决策的扩展式表述中, 自然主体可被直接表示为某个节点.
具体地, 我们需要在:
- 不属于任何决策主体的回合中;
- 任何已经明确表明会受概率影响的决策时;
引入 自然节点. 自然节点 不属于任何决策主体, 并且 从自然节点引申出来的所有分支都受自然节点引入的概率的影响.
自然节点不仅可以对如骰子, 随机数生成器等可以 “产生不确定性” 的物件 (Chance Devices) 进行建模, 还可以将 结果不确定 的情况同样考虑在内. 如在战争中, 基于过往经验的统计规律我们可以 粗略地 估测一些特定的事件发生的概率. 虽然这一方法并不能真实地对特定的实际情况准确地建模, 但用这种方式构建的概率模型是基本可靠的.
处理信息不充分的情形
还是以游戏为例, 下面考虑 牌类游戏. 可知这类游戏的特征是: 决策主体在确定决策时, 受到的影响包括 概率因素 以及 对现状知识的不完备: 任何玩家都不知道其他玩家手上的牌, 因此他们的信息是 不充分的.
同样地, 信息不完整 这一特征也需要在对决策进行扩展式表述时, 用某种方式建模到决策树中.
在此我们所采用的方法是: 将某个决策主体在信息不完整的情况下所有可能做出的决策归类到一个集合中.
如下图所示: 第二层被框选的这些决策节点就属于某个决策主体在对随机掷出的硬币到底是正面朝上还是反面朝上一无所知的情况下所可能做出的决策: 猜测它正面朝上, 或反面朝上.
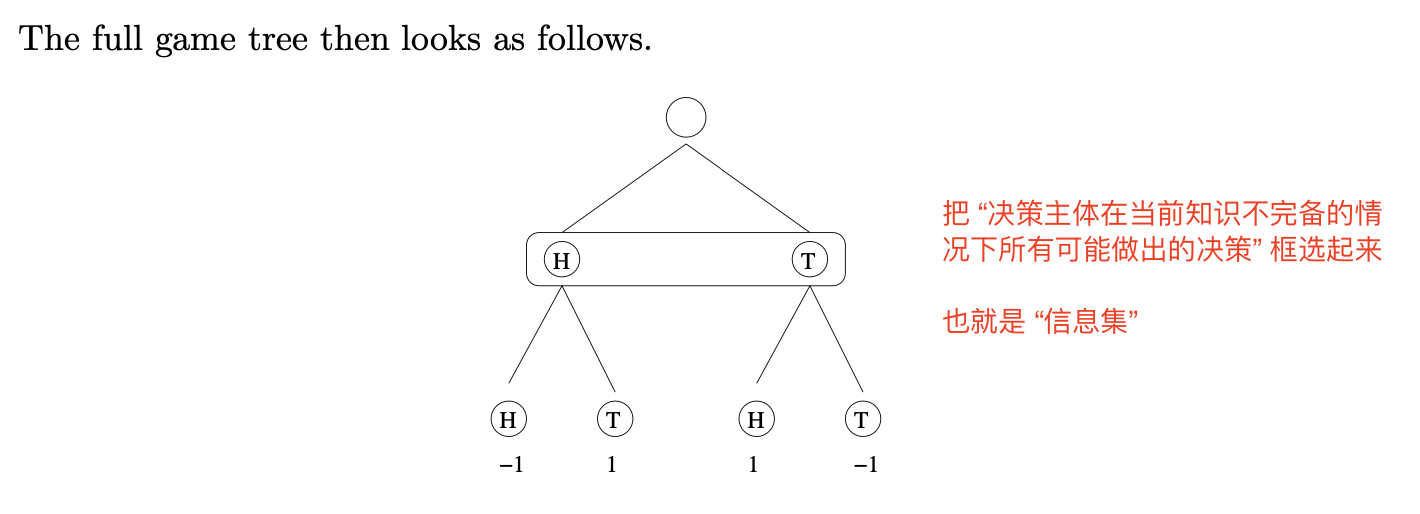
我们称这样的集合为 信息集 (Information Set). 在这一层中, 所轮到的决策主体 必须在缺乏完备信息 的情况下做出某个决策.
不难看出, 如果在某个双人博弈中, 博弈双方都无法知晓对方做出的决策, 即: 双方对当前形势掌握的信息都不完全, 那构造出的决策扩展式表述会包含大量的分支, 变得极其复杂. 因此, 在绘图时为了便于表示, 我们往往会将同一个信息集中的所有决策节点用省略号表示.
博弈的形式化表述
我们随后对 博弈 给出形式化的表述.
定义 (博弈 Game)
博弈 被如下定义:
- 包含一个由有限个决策主体组成的集合
- 包含一棵决策树
- 决策树的每个节点都属于某个决策主体
- 决策树的每条边都被某个动作 (
Action) 唯一标记- 对每个决策主体, 在决策主体所属的层上都有某个 信息集 (
Information Set): 它由一系列决策节点组成, 任意一组决策节点都包含可能被一系列 完全相同 的动作所标记的, 一系列的边.- 决策树的每个叶子节点上, 每个决策主体都被分配了一个 回报 (
Pay-off).

我们称被上述的形式所定义的博弈为 被扩展式表述的博弈 (Game in Extensive Form). 我们将在后文中解释 博弈的正则式表述.
此外还需引入其他的一些重要定义:
定义 (双人博弈 2-Player Game)
称在不考虑自然因素的情况下, 只包含两个决策主体 的博弈为 双人博弈.
定义 (完全和不完全信息博弈 Game of Perfect | Imperfect information)
若博弈中对任何决策主体, 在任何层上的信息集大小都为 $1$, 即 任何决策主体都知道自己当前在完整的博弈决策树上的确切位置, 则称这样的博弈为 完全信息博弈. 它意味着决策主体所做出的任何决策的依据 是完全清晰的, 不包含不确定性.
若在某些节点上, 任何对应的决策主体 不知道自己的对手此前所做出的选择, 也就是 不清楚自己在博弈决策树上的位置, 则称这样的博弈为 不完全信息博弈.
定义 (零和博弈 Zero-Sum Game)
若在任何决策树叶子节点上, 所有决策主体的回报总和都为 $0$, 则称这样的博弈为 零和博弈: 有人赢就必然有人输, 反之亦然, 除非平局, 不存在双赢或双输的局面.
定义 (含随机性和不含随机性的博弈 Game with | without Chance)
若决策树中不存在被自然因素控制的节点, 则称这样的博弈为 不含随机性的博弈, 反之称其为 含随机性的博弈.
需要注意的是:
-
在扩展式表述的定义下, 博弈的决策树 **包含了决策主体双方 多方的, 所有可能的决策路径**. 因此, 决策树中的任何节点其实都包含了一段信息: 也就是 “从起始节点, 决策主体们需要分别做出什么样的决策才会最终让决策路径通过这个节点”. - 进一步地, 我们很难确保 “任何决策主体都能完整地记忆己方和对手在从博弈开始到现在以来做出的所有选择”, 在实际构造博弈策略时, 往往会使用
Cut-Down方法简化需要记忆的步数. 这一策略对 状态循环 的博弈尤其有效. - 上面提到, 某些博弈的状态可能会循环; 同时一些不同的决策路径也可能到达 实质上相同 的节点. 但在扩展式表述中, 为了方便分析和具体实现, 我们会选择将它们作为不同的节点从而避免产生 决策图 而非 决策树.
博弈的策略
为了讨论 “如何在博弈中胜出” 的问题, 我们需要引入 策略 的概念.
定义 (策略 Strategy)
称在某个博弈中, 对某个博弈主体 $i$ 的 完全描述的策略 (
Fully specified strategy) 为:
- 为 $i$ 所拥有的每个决策节点选择博弈决策树所允许选择的某个动作.
- 为 $i$ 的信息集中的所有节点选择相同的动作.

定义 (纯策略 Pure Strategy)
博弈主体 $i$ 的 纯策略 由一个 博弈决策子树 (
Subtree of the game tree) 定义, 它具如下性质:
- 决策树的根节点属于这个策略.
- 在决策子树中, 任何属于 $i$ 的节点上: 子树恰好包含一个可行的决策, 且对同一 $i$ 的信息集中所有节点, 选择的策略相同.
- 决策子树中任何不属于 $i$ 的节点上, 所有的可能决策都属于子树.
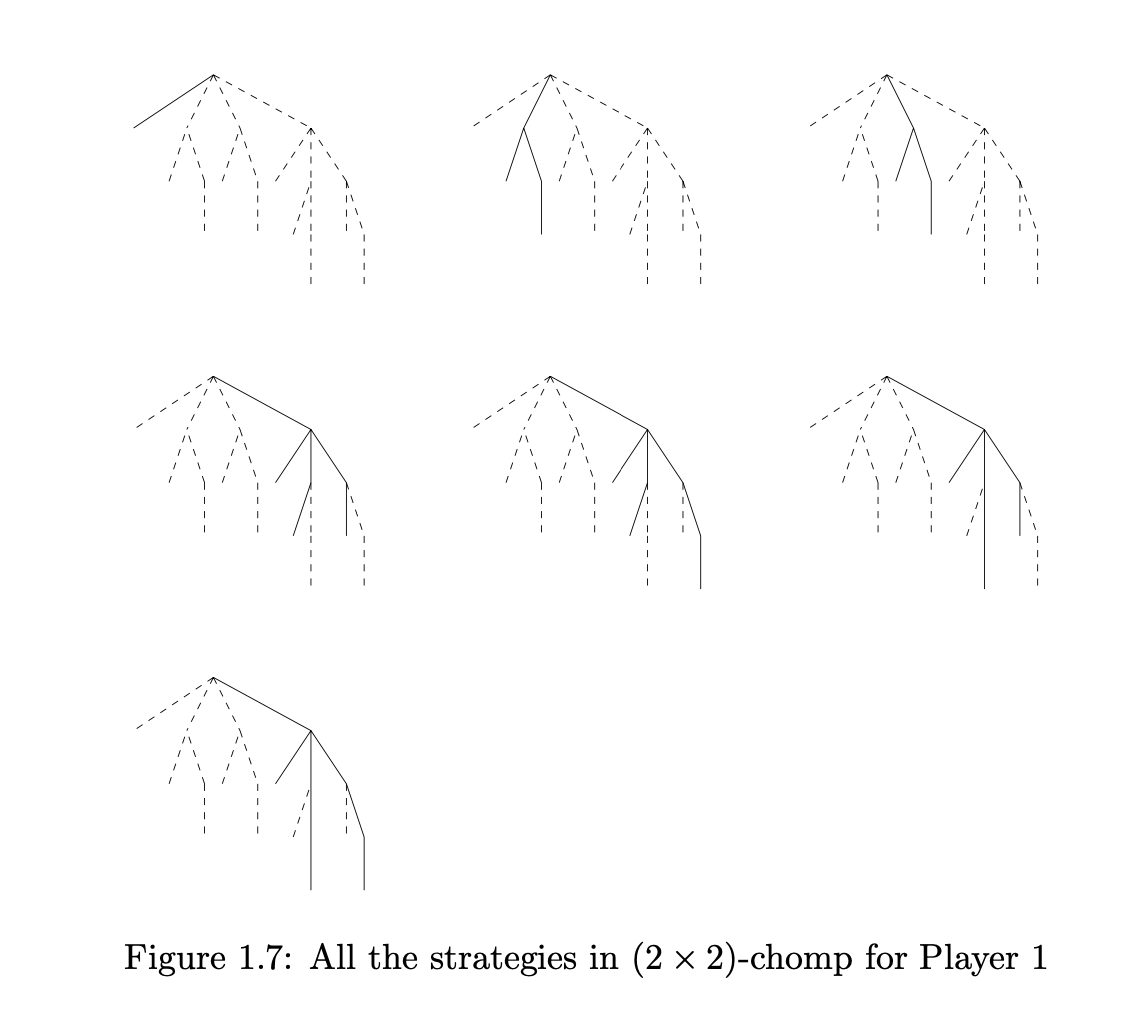
换言之, 博弈的纯策略是 确定 的: 博弈主体必然在可行的策略集合中 选定 一个决策. 如果博弈主体有很多不同的选择, 无法确定 要选择哪个但有选择的 概率分布, 就可以用 决策者概率分布的组合向量 描述它的决策, 这就是 混合策略.
博弈的正则式表述
博弈的 正则化表述 用机械的方式表述博弈中 双方 做出的选择和对应的双方回报. 形式化的定义如下:
定义 (博弈的形式化表述 Game in Normal Form)
我们用下列的方式给出某个博弈的 形式化表述:
- 给定一列大小有限的, 决策主体列表 $1, 2, \cdots, l$.
- 对每个决策主体 $i$, 给定一系列所有可能的策略, 记为 $1_i, \cdots, n_i$.
- 对每个决策主体 $i$, 给定一个 给出其回报的函数 $p_i$. 它以 某个决策路径 为输入, 以 表示回报的数值 为输出.

可以看出, 博弈的正则化表述非常适合描述多方决策同时进行的博弈 (Simultaneous play games). 同时, 若博弈包括超过 $n, ~ n > 2$ 个决策主体, 就需要 $\binom{n}{2}$ 个回报表.
博弈的正则化表述在数学上是高效的, 但在计算上不如扩展式表述合适.

我们同时可以用下列方法给出 博弈大小的估计:

对博弈的求解
此处给出如下的定义:
必胜策略 (Winning Strategy)
无论其他决策主体如何决策, 总是可以确保某个决策主体赢得博弈的策略.
平局策略 (Draw-Ensuring Strategy)
无论其他决策主体如何决策, 总是可以确保某个决策主体最终回报至少为 $0$ 的策略.
并且有如下定理:
定理
对 包含两个决策主体, 信息充分 且不存在 不确定因素, 总是可以在 有限步内终止 的 零和 博弈, 下列情况至少有一个为真:
- 第一个决策主体有必胜策略.
- 第二个决策主体有必胜策略.
- 双方都有平局策略.
我们称, 当这样的策略被找到时, 博弈就是 被求解 的.
同时对博弈的求解也可被分为下列的不同级别:

最后本章内容总结如下:

