启发式搜索算法
本章将回顾和介绍一系列主流的启发式搜索算法.
在博弈论中, 我们可简单的将完整的博弈过程抽象为 “决策树”, 其中每个节点表示博弈的当前状态, 每一条边表示某个玩家在前一节点进行的某种决策, 边所连接的下一级节点表示该决策所导致的结果 (使博弈状态发生了转换). 因此, 要寻找某种制胜策略, 该问题就可被直接转换为: 使用寻路算法寻找树中从根节点到特定叶子结点 的问题.

在上学期的 数据结构与算法 课程中, 我们已经系统地学习了数种可在树中寻找最短路径的寻路算法. 我们下面从 Dijkstra 算法开始回顾, 并详细介绍基于它的, 引入 启发式思想 的 A* 算法.
Dijkstra 狄杰斯特拉寻路算法
Dijkstra 算法作为寻路算法, 其目的自然是: 寻找从起始节点到图中任意其他节点的路径.
它的核心逻辑是: 在做出下一步决策时, 在 当前节点可达到的新路径 中选择 路程最短的. 在算法实现中我们一般使用一个 优先序列 (Priority Queue) 存储所有可能的路径选择.
同时可知: 基于上述的性质, 任何节点被从优先序列中弹出时 (Dijkstra 算法认为找到了从起始节点到它的最短路径时), 算法所找到的路径 必然是 最短路径.
由此 Dijkstra 算法具备下列的特征:
- 算法寻找的是 全局最优解.
- 算法具有 完备性 (
Complete): 只要确实存在某个最优解, 则Djikstra算法一定能找到它. - 算法具有 无信息性 (
Uninformed), 它在寻路时不利用任何对目标节点的知识.
Greedy 贪心算法
在介绍贪心算法前, 需要引入 启发式 (Heuristic) 的概念.
定义 (启发式 Heuristic)
称启发式为: 基于 直观 或 经验 构造的, 用于解决优化问题的策略. 启发式算法在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解, 且该可行解与最优解的偏离程度一般 不能被预计.
回到寻路问题, 从人类的角度看最符合直觉的寻路策略是: 在每一步选择时, 都尽可能地选择 距离目标最近 的路径, 这一思想就是 从人类直观中得到的启发.
要实现这样的寻路算法, 我们就需要定义一个 启发函数 (Heuristic Function):
方便起见记该启发函数为 $h(x)$, 它是对 从当前点 $x$ 到目标点之间距离的估计.

由此我们可以如此实现贪心算法: 从起始点出发, 始终基于启发函数 $h(x)$ 给出的, 和目标点距离最 小 的路径, 重复这一过程直到找到通往目标点的路径为止.
贪心算法存在这样的问题: 由于它在任何一步执行选择时都不考虑全局最优性, 而单纯关注 局部最优.
贪心算法的局部最优性同时导致:
- 所生成的解 很可能并不是我们想要找到的最优解
- 不具备完备性: 即使最优解实际存在, 它也可能永无法找到它.
贪心算法同时具备下列的特征:
- 贪心算法在特定的任务场景 (如由一系列局部最优总是可以得到全局最优的动态规划问题) 下可以达到很高的性能.
- 贪心算法是 有信息性 (
Informed) 的: 为了得到合理的启发式估计, 我们需要具备对该问题本身的 领域知识 (Domain Knowledge). - 将贪心算法和回溯算法结合可使其 具备完备性.
A* Algorithm A*算法
至此我们已经介绍了在寻路中致力于最小化 已投入的代价 的 Dijkstra 算法和致力于最大化 当前回报 的贪心算法.

通过将二者结合, 我们即可得到所谓的 A* 算法:

何为合理的启发式算法
我们下面讨论 合理的启发式算法 所需要具备的基本性质.
此处给出三个性质:
-
Admissible可接受性:启发项在对 当前解到目标最优解之间的距离 的估计上必须是 乐观 的, 也就是其估计必须是
Underestimate.
-
Monotonic | Consistent单调性一致性: 启发项对路径的估计必须满足下面所示的 三角不等式:
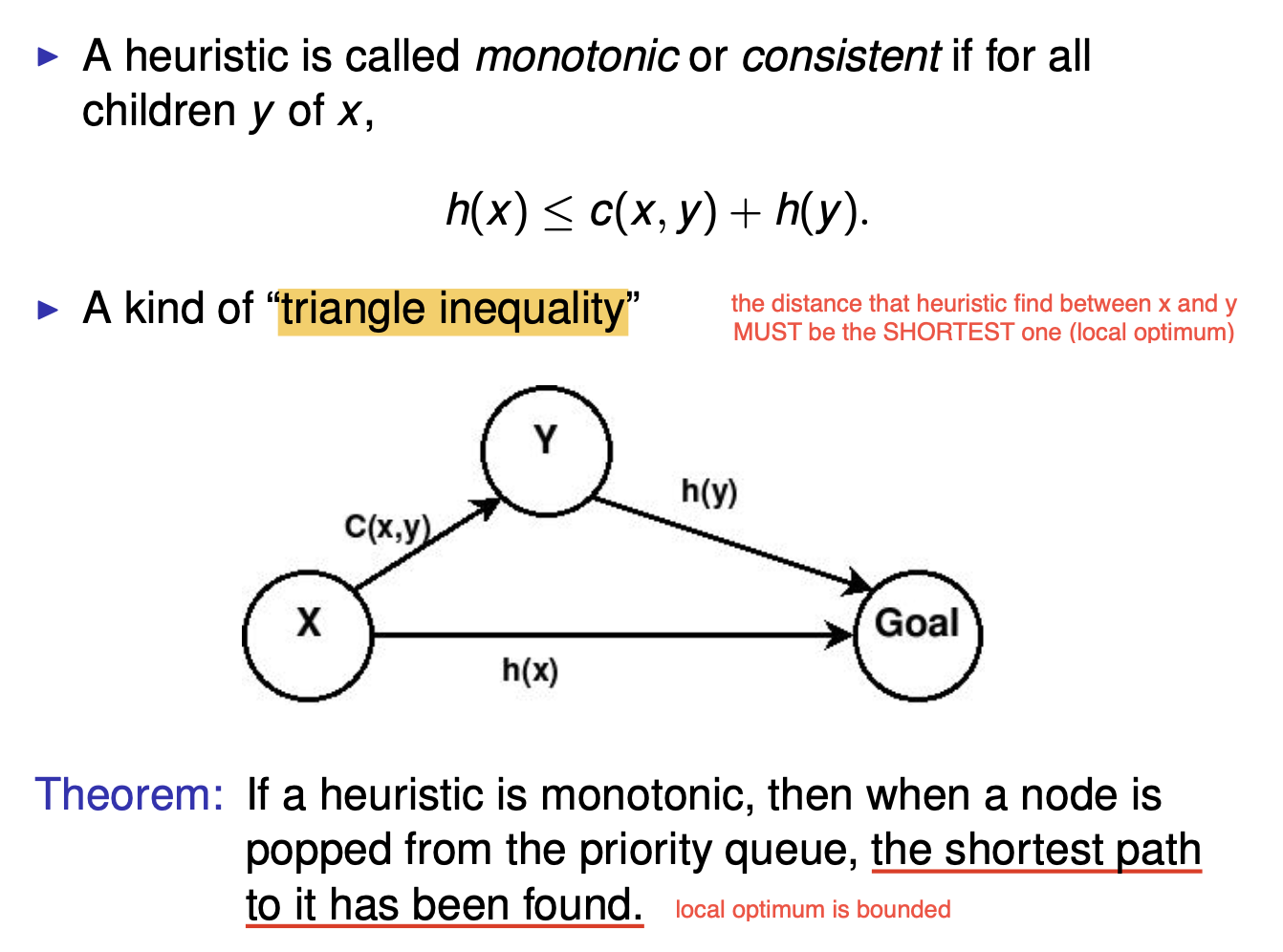
-
Informative信息增益性:启发项需确保, 随着搜索时当前位置越接近目标, 它所能提供的信息价值越高 (它对剩余距离的估计越来越准确).

注意, 不同启发项之间所具备的信息增益性可以 相互比较. 理想状态下最有价值的启发项提供的信息 恰好和实际的距离相同, 而最没有价值的启发项无法提供任何距离信息. ]

需要注意, 一个可用的启发项 必须满足可接受性和单调性, 但不一定需要具备很高的信息增益性.
