曲线建模理论
本章主要介绍对 曲线 的一般建模方法.
一般地, 计算机图形管线包含三个部分: 建模 (Modeling), 帧动画 (Step Animation) 和渲染 (Rendering). 下面首先讨论第一部分: 建模.
建模的主要目的是 构建几何图形, 而几何图形的本质是一系列有序的, 通过 直线 互相连接的 顶点, 可通过多边形网格 (Polygon Mesh), 点云 (Point Cloud) 等方式表示.
1. 对曲线的基本定义
在一些特殊的应用场景, 如 3D建模, 构建相机路径, 矢量图 等情形下, 我们需要对 曲线 进行建模. 下面简述几种曲面建模的一般方法.
在计算机图形学中, 定义曲线的方式有下列两种:
- 一系列的点坐标组成的一维数组
- 一个 (一维或 $n$ 维的, 取决于曲线所在空间维度的) 映射.
上述两种定义有不同的优越性. 第一种定义便于在曲线上生成新的点, 第二种定义便于描述轨迹 (Trajectory).
下面引入定义: Speedline (速度线).
定义 1.1 (速度线 Speedline)
称 连接两个或多个 由 某个数学公式确定的顶点 的曲线为 速度线, 由于其曲线形态完全由它所连接的顶点决定, 又称这些顶点为 控制点 (
Control Points).
速度线可用于 拟合 控制点实际所在的曲线, 更多的控制点可使速度线更接近于 平滑的曲线, 这一过程也被称为 栅格化 (Tessellation):
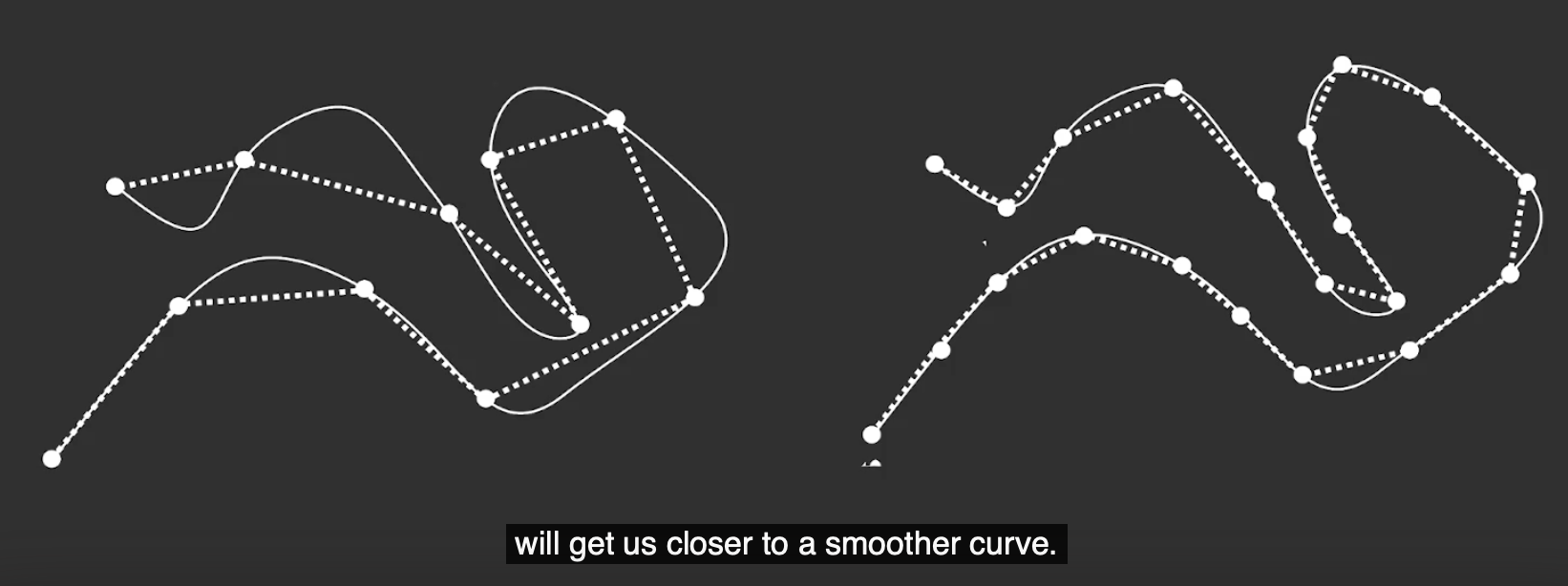
其次引入另外两个重要的定义:
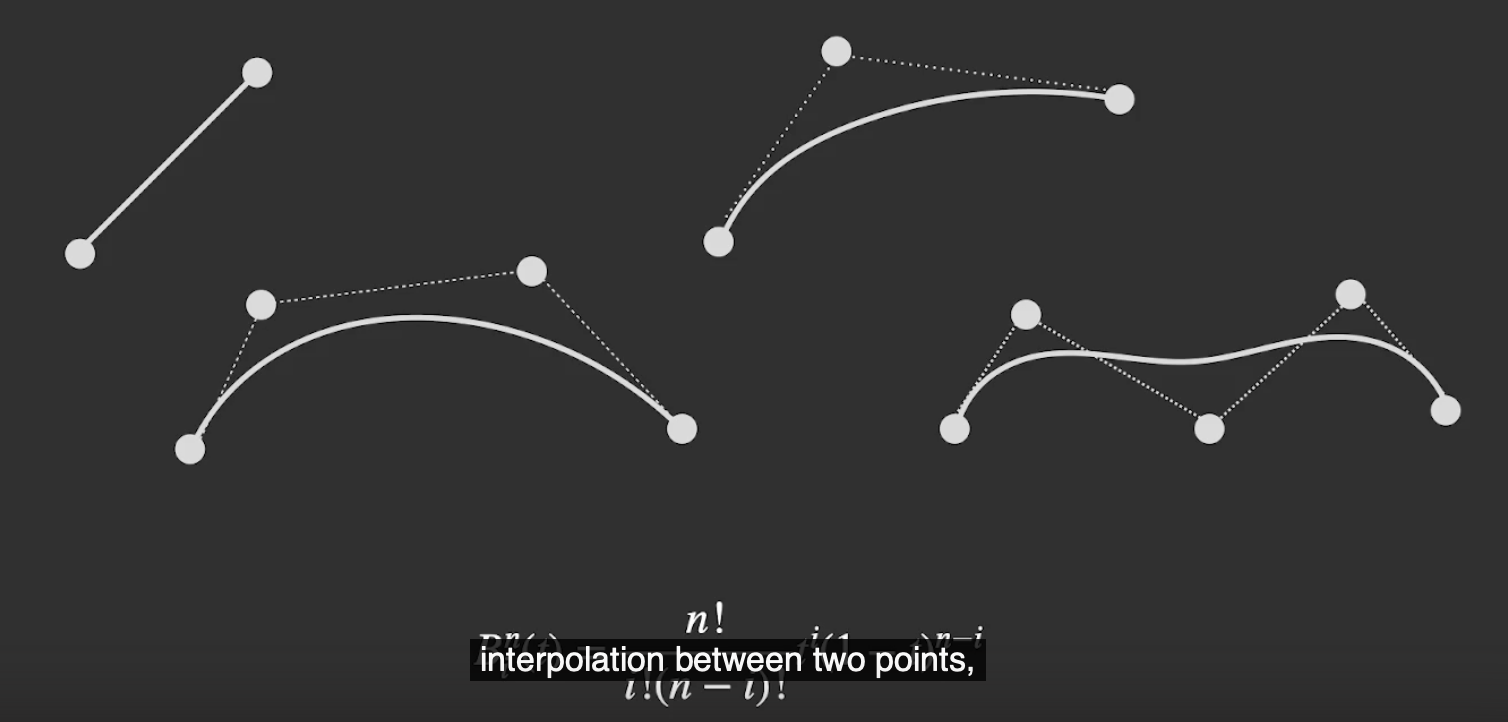
定义 1.2 (插值 interpolation)
称在离散数据的基础上构造一条 可以通过全部给定的离散数据点 的曲线的行为为对给定离散数据的 插值. 这条曲线可以由某个 连续函数 所表示.
定义 1.3 (近似 Approximation)
称基于给定的一系列离散数据点构造出一条 不完全通过所有离散数据点, 但大致可以反应其走势 的曲线的行为为对给定离散数据的 近似.
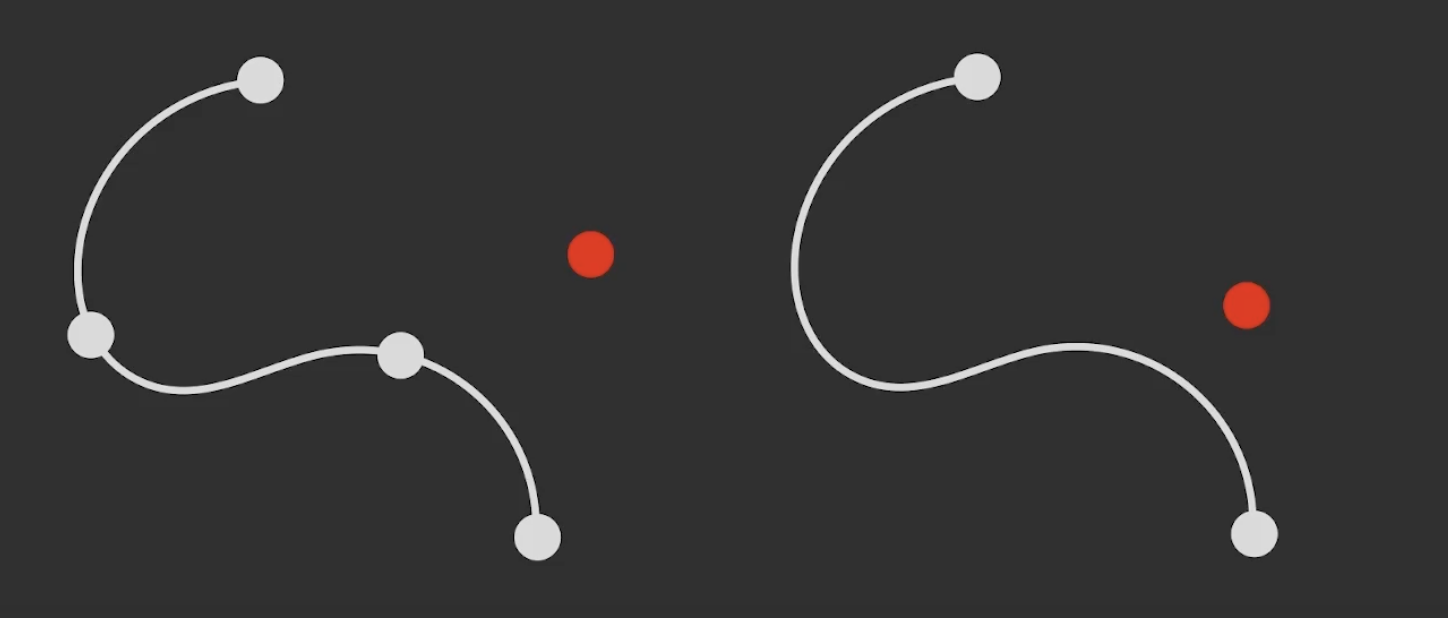
如上图所示, 左侧的曲线就是对线上四个离散点的插值, 而右侧的曲线只通过了四个离散点的其中两个, 因此是对这四个离散点的近似.
2. 三次贝塞尔曲线
下面我们主要讨论 三次贝塞尔曲线 (Cubic Bezier Curve).
定义 2.1 (三次贝塞尔曲线 Cubic Bezier Curve)
三次贝塞尔曲线是基于下列规则所定义的拟合速度线:
- 给定四个控制点: 两个插值点 $P_0, P_3$ 和两个近似点 $P_1, P_2$.
- 对两个插值点进行曲线插值, 此时该曲线同时可视为对另外两个点的近似.
由此得到的曲线是一条 位于给定四个控制点围成的凸四边形 (
Convex Hull) 平面范围内 的 三次多项式 表示的 曲线, 它在两个插值点处 相切.$P_0$, $P_1$, $P_2$, $P_3$ 四个点在平面或在三维空间中定义了三次贝塞尔曲线.
曲线起始于 $P_0$ 走向 $P_1$, 并从 $P_2$ 的方向来到 $P_3$. 一般不会经过 $P_1$ 或 $P_2$, 这两个点只提供 方向资讯. $P_0$ 和 $P_1$ 之间的间距, 决定了曲线在 转而趋进 $P_3$ 之前, 走向 $P_2$ 方向的 “长度” 有多长.
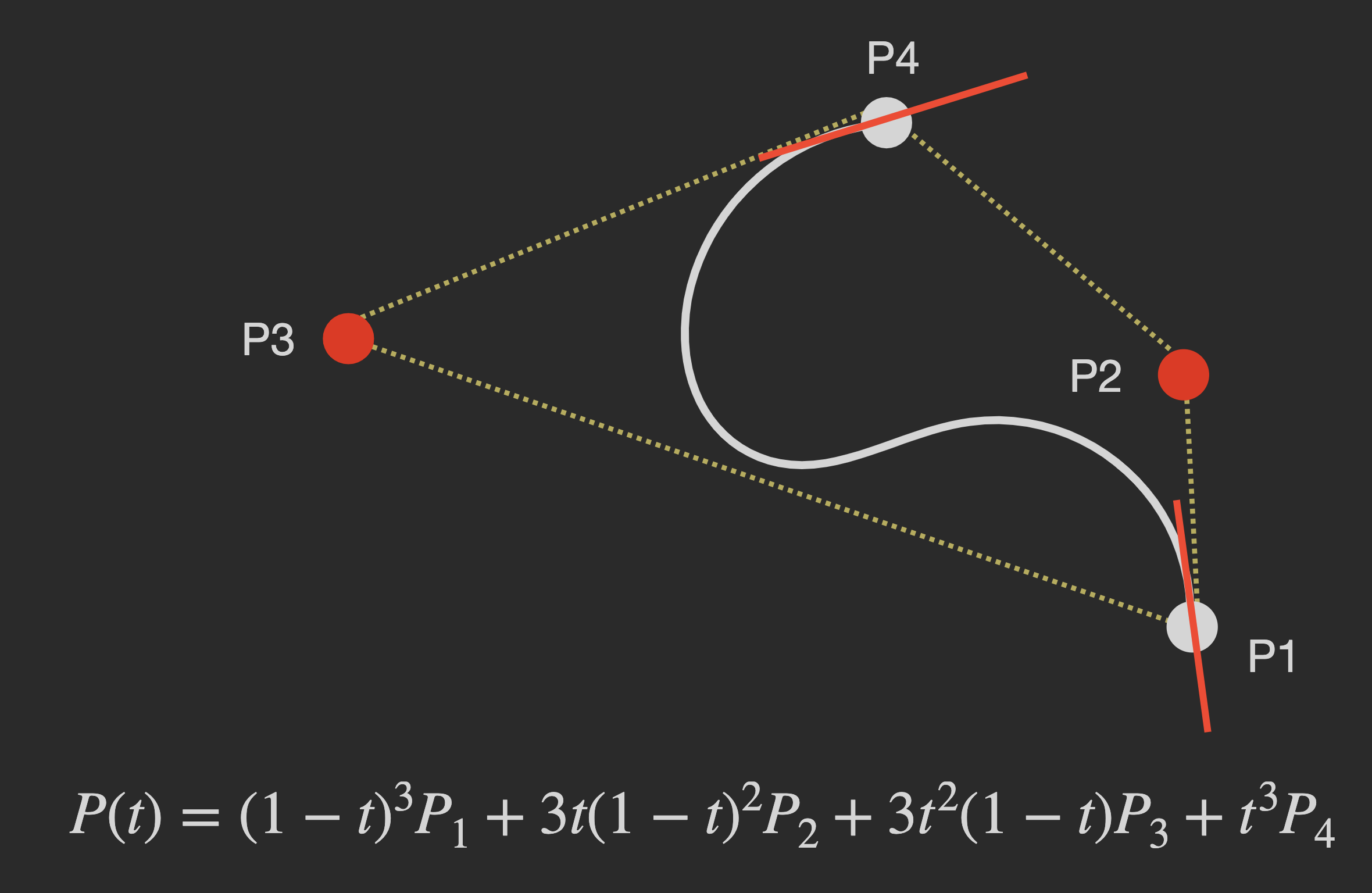
同时可看出, 三次贝塞尔曲线的参数表达式为:
\[P(t) = P_0(1-t)^3 + 3P_1t(1-t)^2 + 3P_2t^2(1-t) + P_3t^3.\]在本课程中, 出于便于展示贝塞尔曲线表达式的基多项式的目的, 此处给出的贝塞尔曲线表达式将四个控制点的对应权重全部设为了 $1$.
在贝塞尔曲线的参数表达式中, 控制点的权重 $P_1, \cdots$ 分别表示了 每个控制点 对基于 $t$ 的贝塞尔曲线值的 贡献权重.
实际上, 通过调整控制点的权重我们可以生成具有不同性质的 缓动曲线. 下面我们基于这一假设继续讨论.
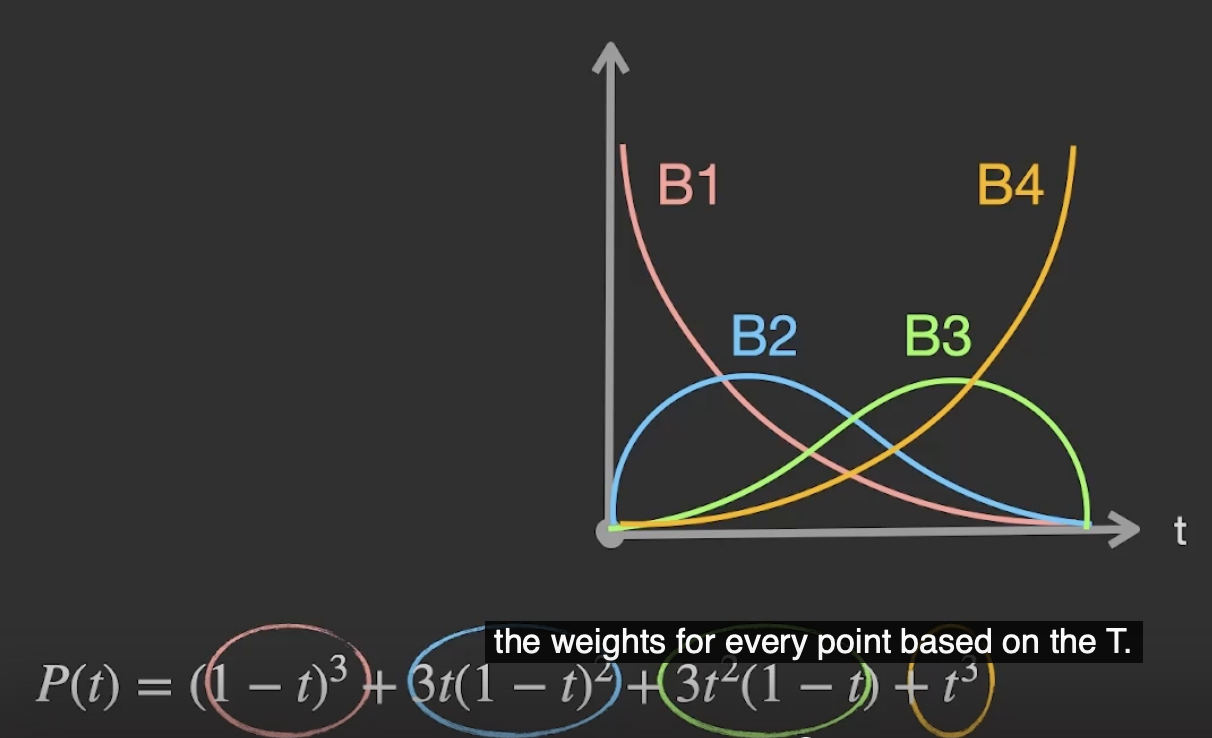
如上图所示, 这四个多项式就是组成三次贝塞尔曲线表达式的 基多项式 (Base Polynomial).
2.1 三次贝塞尔曲线的矩阵运算表示
同时为了方便计算和存储, 一般速度线公式 可表示为下列所示的矩阵运算形式:

其中几何部分 (Geometry, 记为 $G$) 存储了三次贝塞尔曲线的四个控制点, 贝塞尔曲线系数部分 (Spline Basis, 记为单词 “ Bezier” 首字母 $B$) 存储了系数, 最后的幂基 (Power Basis, 记为 $T$) 则是一系列 正则单项式 (canonical monomial), 这个复杂的矩阵表示的计算结果就是 由给定的四个顶点作为控制点 的 三次贝塞尔曲线 的 完全展开式.
需要注意: 幂基矩阵 Power Basis 所存储的是 四维线性空间的一组基, 它们之间是 彼此线性无关 的, 可以用来表示任意的三次多项式.
幂基 只是多项式线性空间中最简单的一组基. (根据线性代数知识我们知道, 线性空间有无数组基), 下面讨论多项式空间中另一种常用的基: 伯恩斯坦基 (Berstein Basis).
2.2 伯恩斯坦基
定义 2.2 (伯恩斯坦基, Berstein Basis)
伯恩斯坦基是由 伯恩斯坦多项式 组成的, 定义 $n$ 次伯恩斯坦多项式为:
\[B_{i, n}(t) = \binom{n}{i} t^i (1-t)^{n-i}.\]因此可知, 给定 $n$, 共有 $(n+1)$ 个伯恩斯坦多项式.
可见, 三次贝塞尔曲线可看作 一组伯恩斯坦基的线性组合. 一般地, 我们将参数 $t$ 定义在 $0 - 1$ 区间内.
此外可知, 三次贝塞尔曲线四个控制点的权重全部被设置为 $1$ 时, 可知在 $t \in [0, 1]$ 时其值 $P(t)$ 恒为 $1$, 我们称这一性质为 单位分解 (Partition of Unity) 性质, 这也是三次贝塞尔曲线 永不会超出四个控制点围成的凸包 (Convex Hull) 之外 的原因.
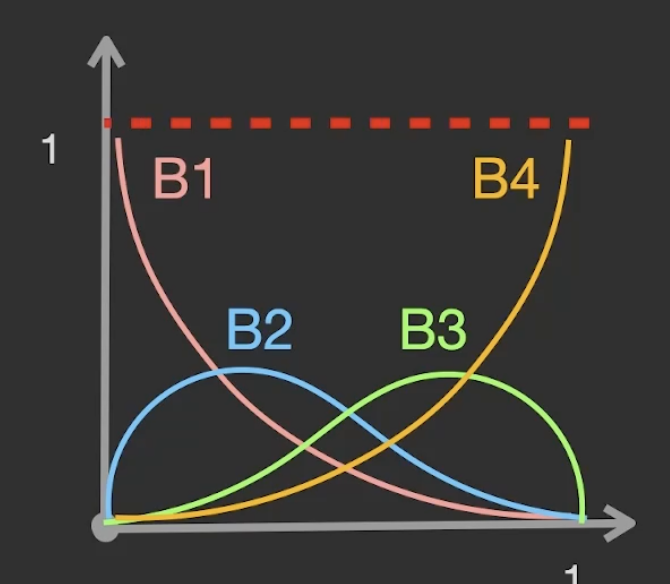
下面讨论伯恩斯坦多项式的值 $[B_1(t), B_2(t), B_3(t), B_4(t)]$ 和正则基 $[1, t, t^2, t^3]$ 的转换. 通过简单的矩阵运算即可做到:

2.3 升阶: 用高维贝塞尔曲线建模
三阶贝塞尔曲线是最为常见的曲线表示方式, 但我们也可以在必要的时候用更高阶的贝塞尔曲线进行建模. 从上面伯恩斯坦基的定义可以看出, 通过调整 控制最高维 的参数 $n$, 我们可以决定这组伯恩斯坦基的维度, 进而 用这组伯恩斯坦基组成更高维的贝塞尔曲线.
要对现有的, 使用低维贝塞尔曲线表示的曲线进行表示上的升维, 我们只需要对现存的控制点进行 平均插值, 然后单独决定新生成的这些控制点在贝塞尔曲线表达式中的对应权重.
由于 每个控制点 都会影响整条曲线的形状, 因此高维贝塞尔曲线的使用远比低维复杂.
2.4 简化: 贝塞尔曲线的拆分
下面讨论对三维贝塞尔曲线的拆分 (Subdivision).
在一些情况下我们 既希望对贝塞尔曲线的形状进行更精细的控制, 又 不希望引入高维贝塞尔曲线在曲线形状控制上的复杂度. 此时, 我们可以使用下列的 拆分 技巧将一条贝塞尔曲线拆成两个部分, 单独控制每个部分的形状.
下面还是以三次贝塞尔曲线为例. 需要注意: 对贝塞尔曲线的降阶并不会降低曲线原生的复杂程度, 拆分后的两条曲线 仍然是三次贝塞尔曲线, 只不过在拆分后, 我们就可以分别调整两条曲线, 形成更复杂的图形.
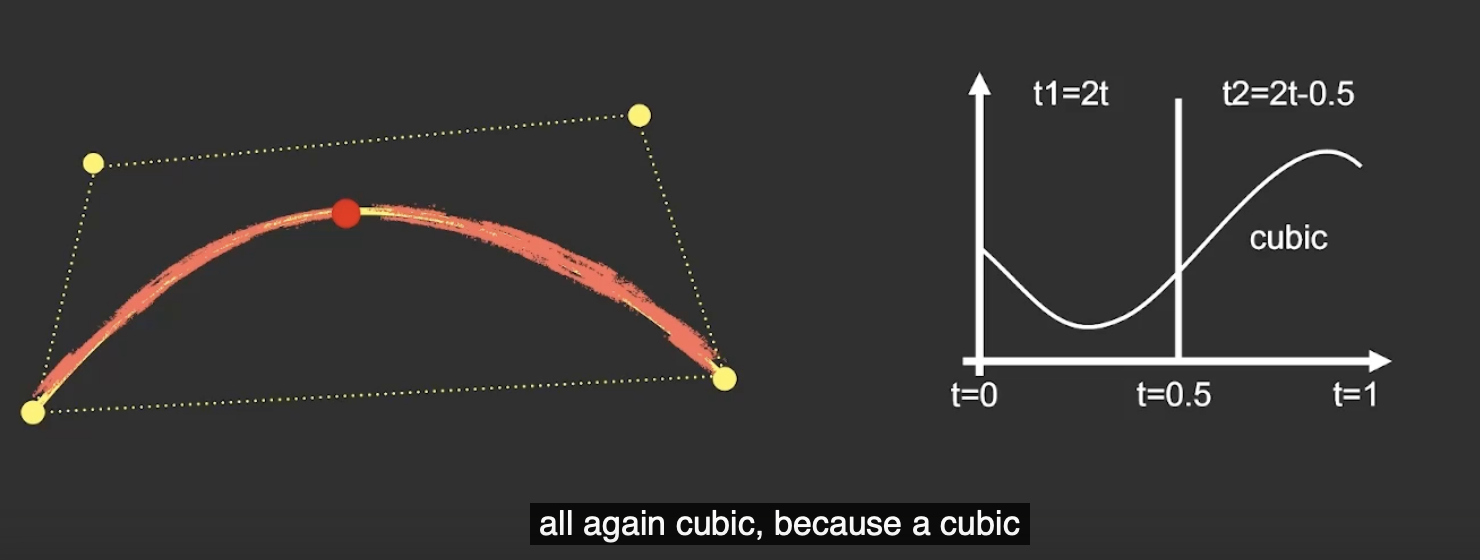
下面讨论拆分的具体算法.
首先将除了曲线凹面的控制点连线排除在外, 对剩下的三条连线各取 中点.
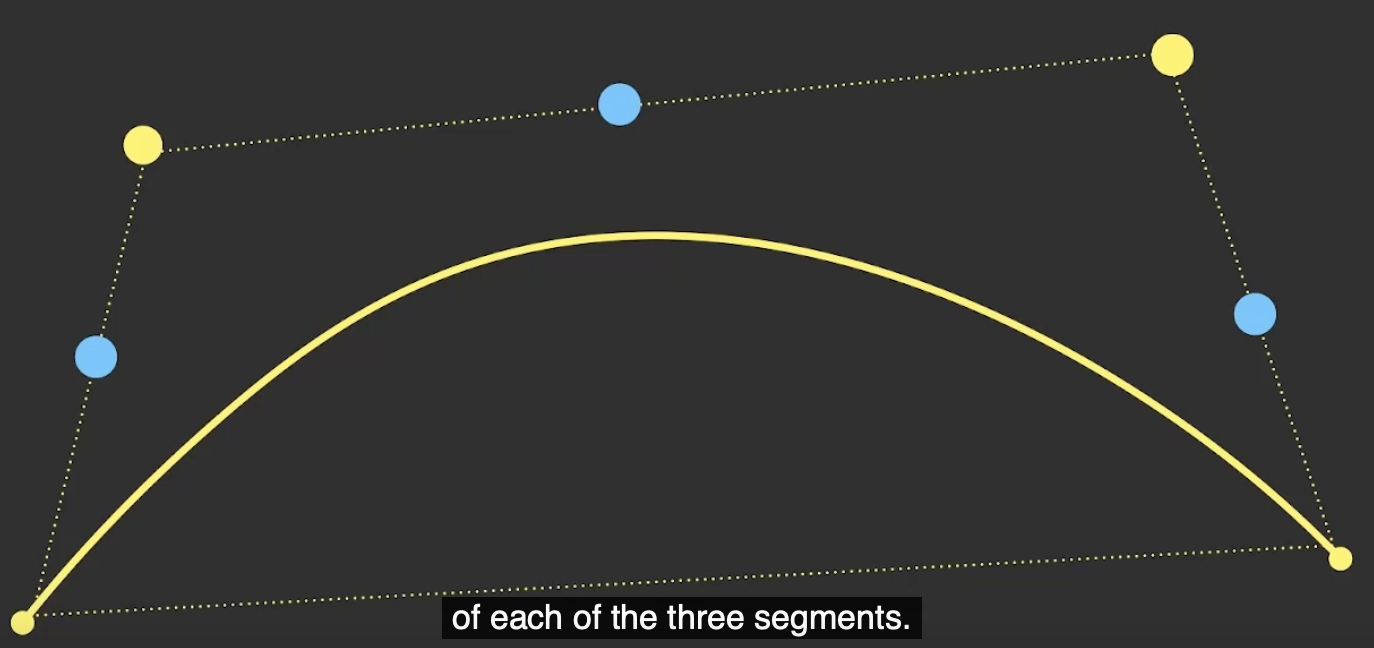
连接这三个中点, 然后再取得到的两条连线的中点.
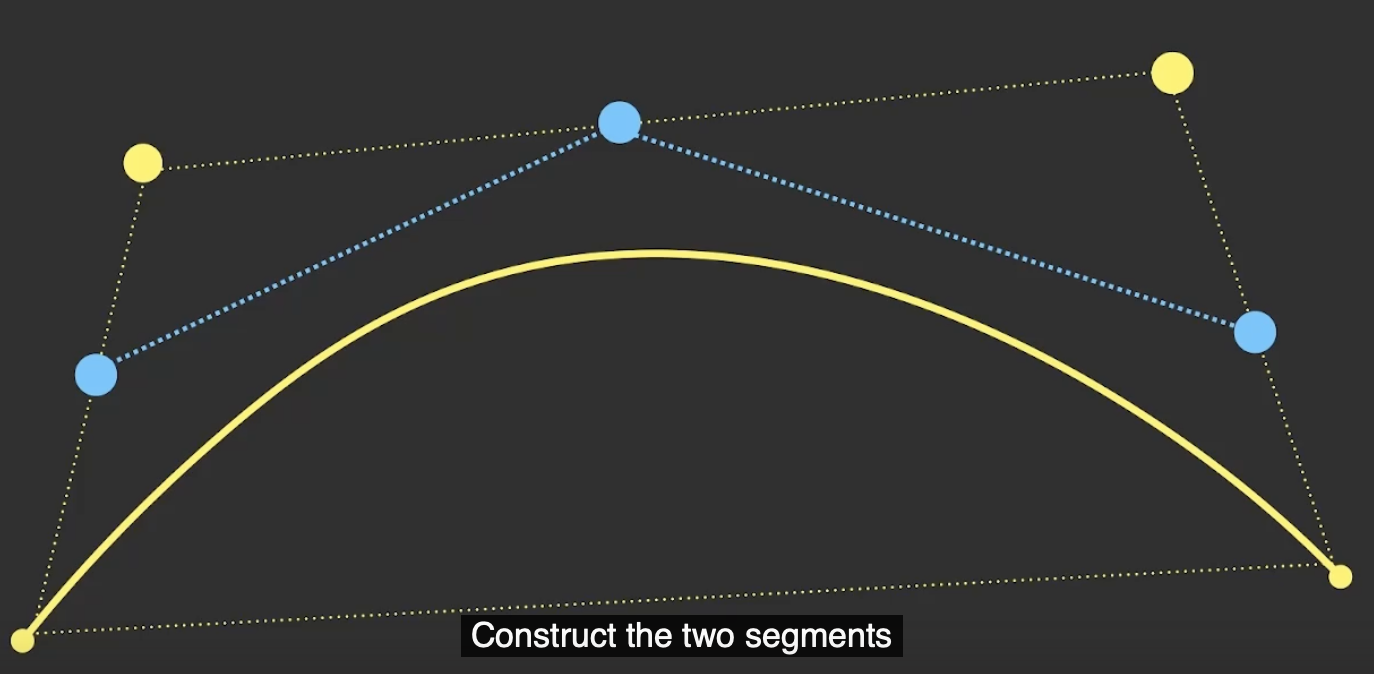
再连接 这两条控制点中点连线的中点连线, 它将会和曲线在某一点 相切.
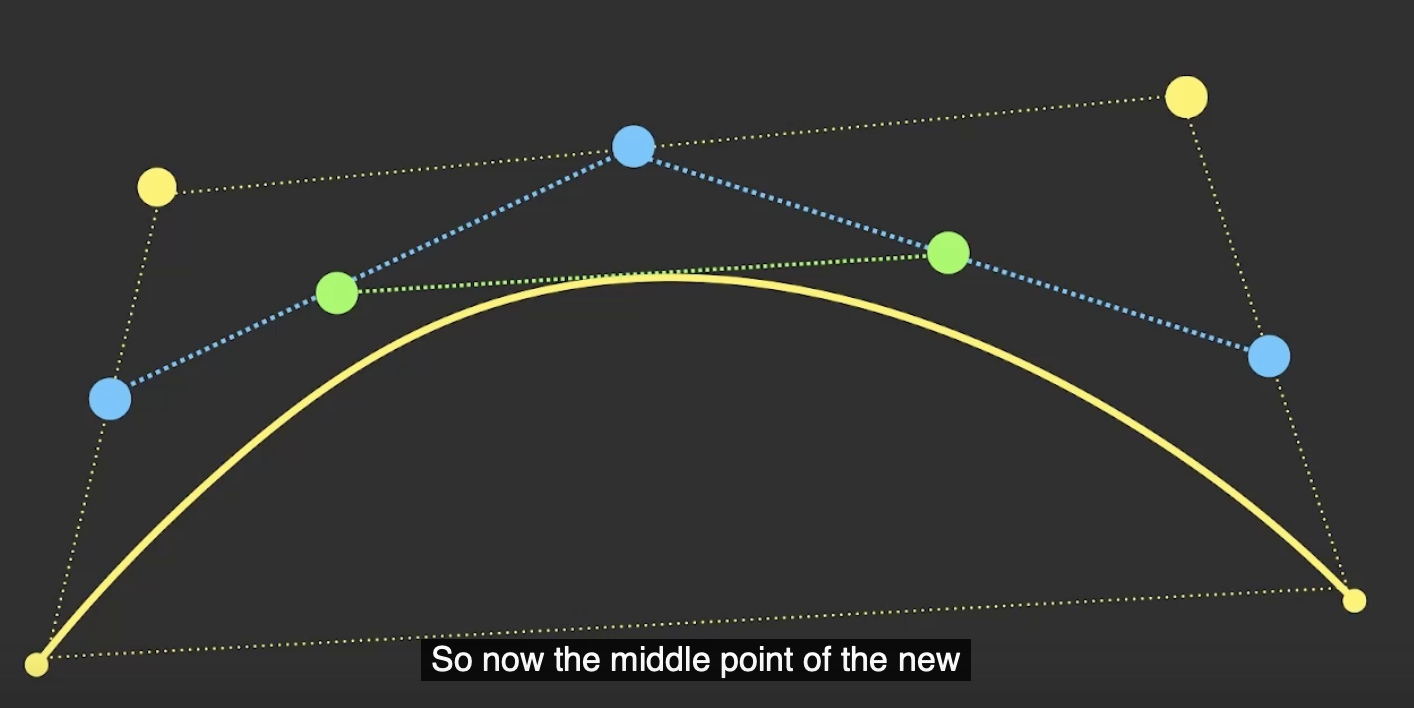
此时相切的这个点就是 对这条贝塞尔曲线的拆分点.
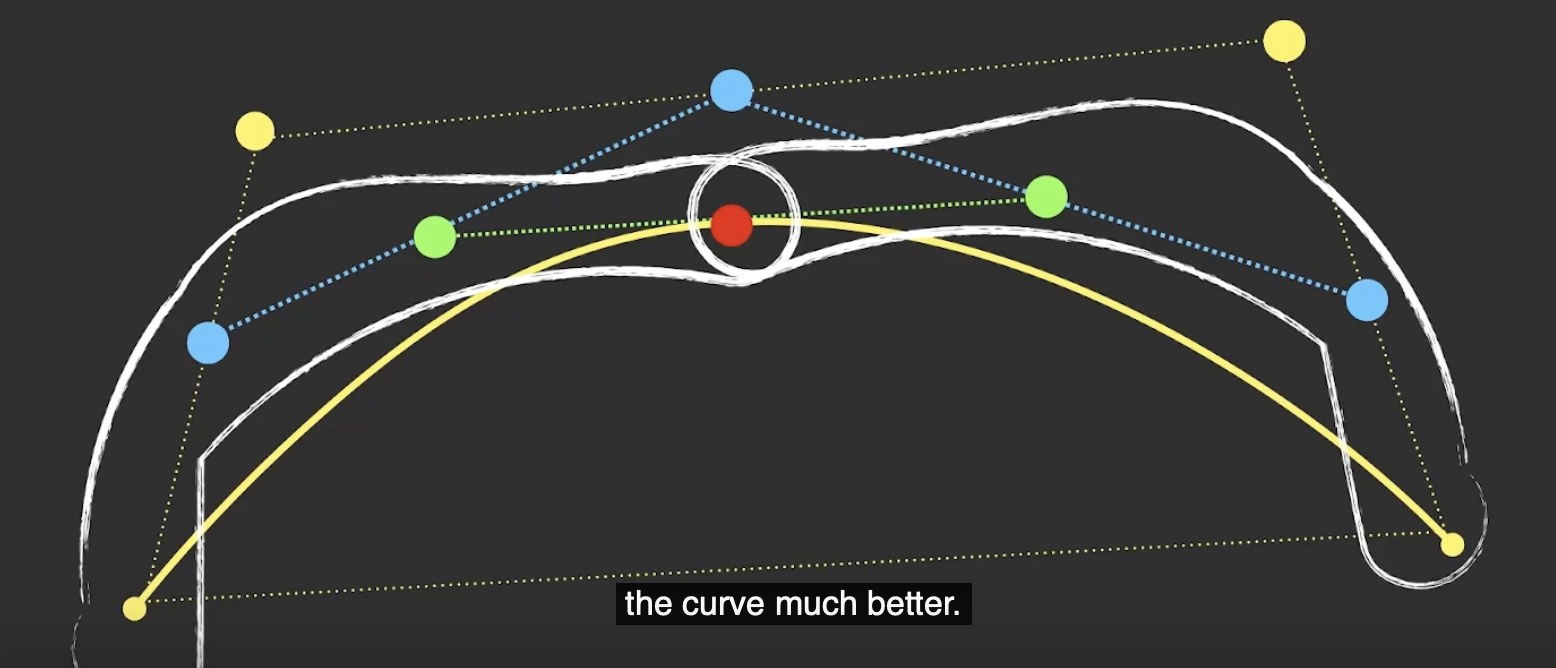
可以看到, 被拆分的两条曲线也是三次贝塞尔曲线, 我们可以通过控制它所属的控制点对应的权重决定它的形状.
注意: 此处对于三次贝塞尔曲线, 在拆分它时我们进行了两次这样的操作. 一般来说, 对于 $n$ 次贝塞尔曲线, 我们需要进行 $n-1$ 次这样的 “取中点” 操作才能找到它的拆分点.
3. 曲线的微分性质 (Differential Property)
从现实出发, 在为曲面着色时所需要进行的, 对 曲面法线 (Surface Normal) 的计算, 渲染动画时对物体运动加速度的计算, 以及对曲线平滑程度的分析都需要涉及到 曲线的微分性质.
下面以如图所示的曲线为例, 假设该曲线为某个物体的运动曲线, 计算它的速度.
要根据物体的运动曲线计算其速度, 就需要首先知道这条曲线的 导数. 分析上我们不难通过 对该曲线表达式关于其唯一的参数 $t$ 求导 得出它的导数.
以贝塞尔曲线为例, 由于它在定义域 $[0, 1]$ 上是 连续 的, 因此它在定义域上同样 处处可导.
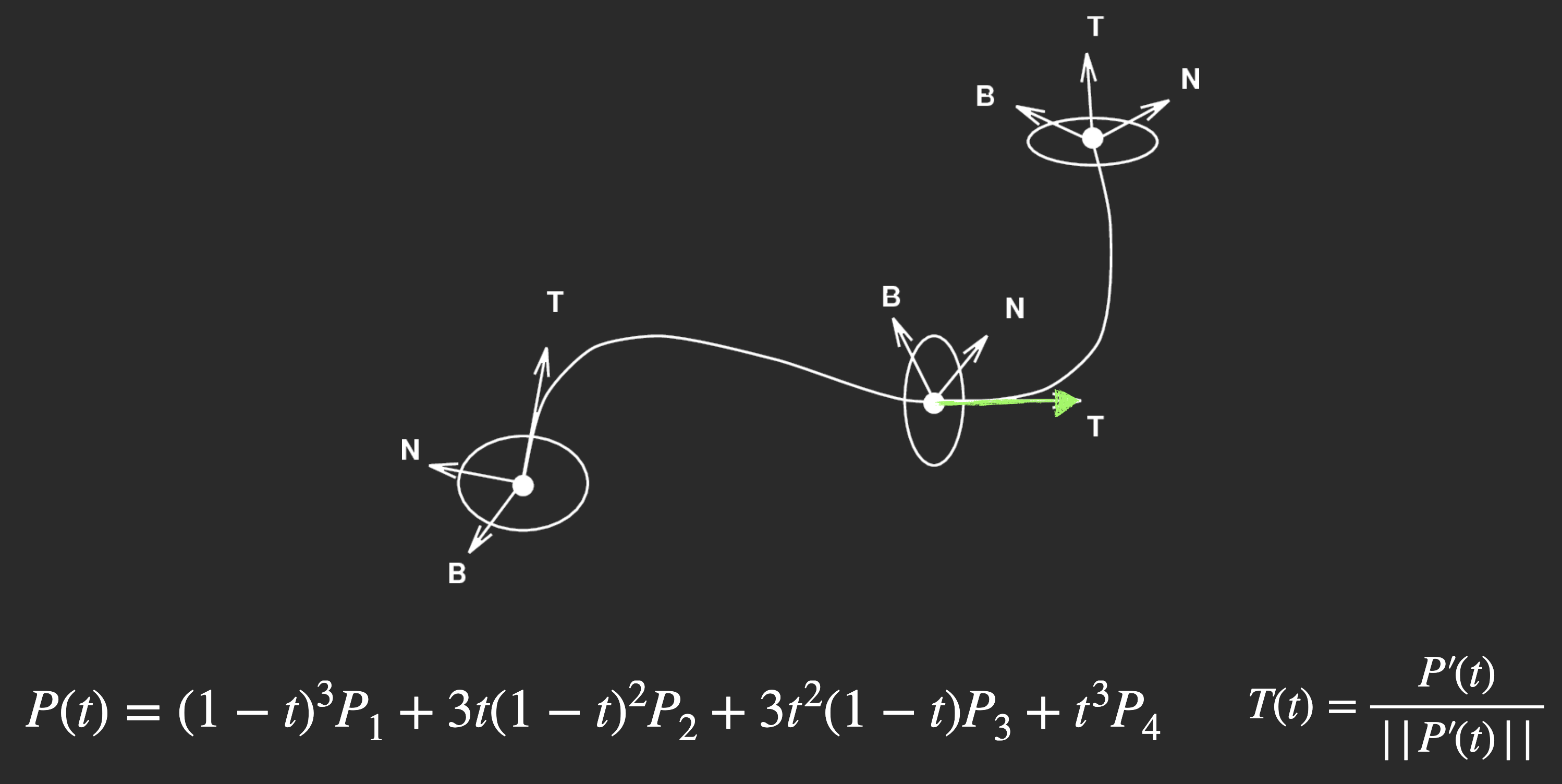
注意此处对切线的定义:
下面讨论计算机图形学中的一个重要概念: 曲线的 连续性.
定义 3.1 (计算机图形学意义上的曲线连续性)
在计算机图形学中我们如下定义三种连续性:
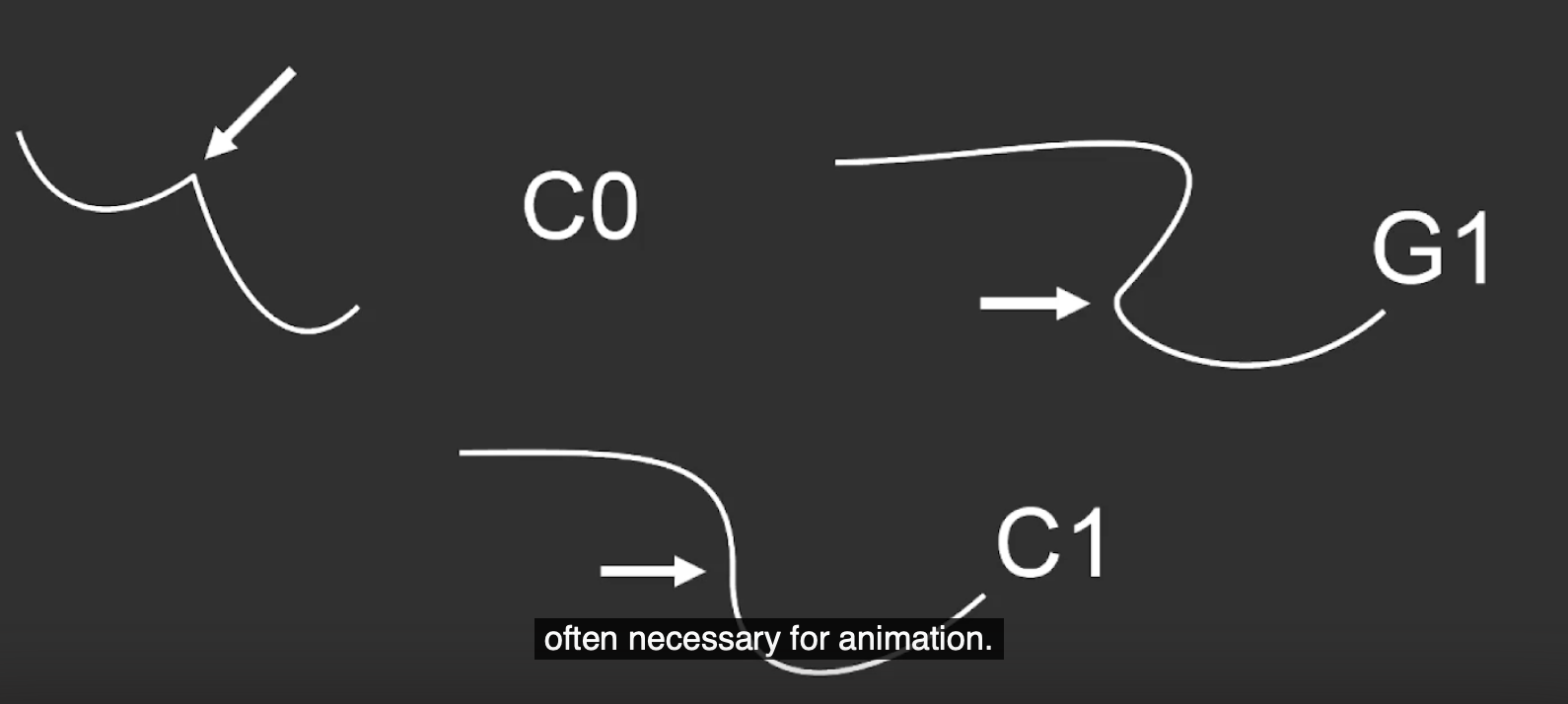
$C0$: 最基本的 连续性指标, 只要两条曲线 相连 即可, 不关心它们之间的连接平滑与否.
$G1$: 又称为 几何连续性 (
Geometry Continuity), 只要两条曲线在它们相接的地方 切向量的方向一致 即可满足. 在大多数情况下 (如建模) 曲线连接只要满足 $G1$ 性质即可.$C1$: 称为 参数连续性 (
Parametric Continuity), 两条曲线需要在 连接处拥有相同的切向量 (也就是一阶导数相同, 切向量的方向和大小都一致, 反映出来的信息就是: 如果这条曲线是某个物体的运动曲线, 则物体在这一点上, 运动的 方向 和 速度 都一致). 因此对 动画 而言, $C1$ 级别的曲线连续性已基本足够.$C2\backslash C2+$: 更强的连续性性质, 在本课程中不详细介绍. 简单来说 $C2$ 需要曲线在连接处 除了切向量相同, 二阶导数也需相同.
除此以外还有更强的 $Cn$ 连续性, 它表示曲线除了要满足 $C(n-1)$ 阶连续性外, 在结合点的 $n$ 阶导数也要相同.
4. B-样条曲线 (B-Spline)
我们此前介绍了第一种建模曲线的方法: 使用贝塞尔曲线建模. 这一方法的主要问题在于:
- 贝塞尔曲线的 拼接非常复杂 , 要想得到理想的结果需要确保拼接的曲线满足几何连续性或参数连续性.
- 贝塞尔曲线的次数由其 特征多边形的顶点数 决定 (注意到任何贝塞尔曲线的次数总等于其特征多边形的顶点数 $-1$).
- 贝塞尔曲线的控制点对曲线形状的影响是 全局 的: 修改任何一个控制点, 整条曲线的形状都会发生变化, 无法对贝塞尔曲线进行 局部修改.
为了缓解这些问题, 我们又引入了 B-样条曲线.
定义 4.1 (B-样条曲线)
定义 B-样条曲线为:
给定 $m+1$ 个 分布在 [0, 1] 区间上 的节点 $t_0 < t_1 < \cdots t_m$, 称 $n$ 次 B-样条 是一个参数曲线:
\[S: [0, 1] \rightarrow \mathbb{R}^{2}\]它由 $n$ 次B样条基 组成:
\[S(t) = \sum_{i=0}^{m}P_{i} b_{i, n}(t), ~~ t \in [0, 1].\]并且称这些点 $P_i$ 为 控制点.
称这样的参数曲线为 $n$ 次B-样条曲线.
B-样条曲线的主要优点在于:
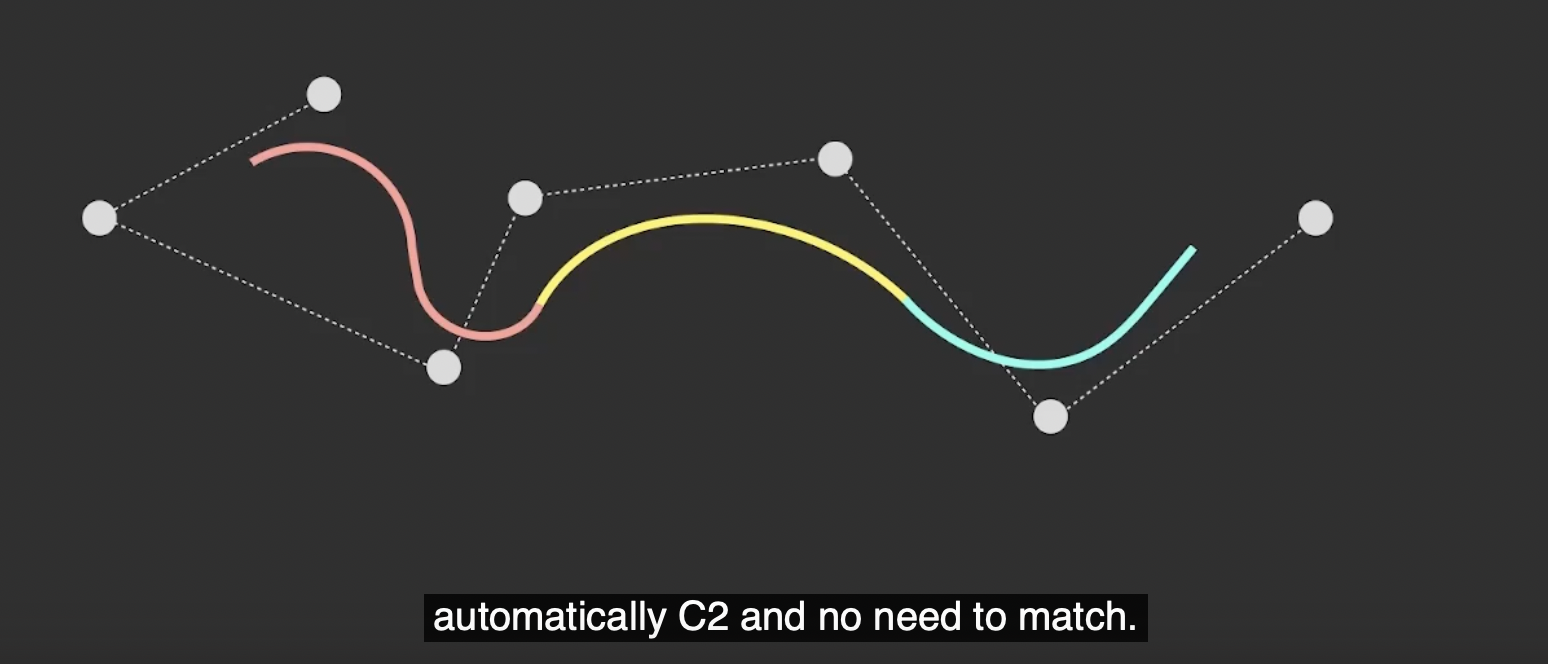
- 天然满足最强的 $C2$ 连续性, 无需像贝塞尔曲线那样在拼接时还得检查两条曲线端点处的切线, 确定曲线之间的接合处满足几何连续性或参数连续性, 任意多条B-样条曲线首尾相连得到的曲线必然是 处处满足 $C2$ 连续性 的.
- 控制点的数量和曲线表达式的次数无关, 由此大大简化了复杂曲线的表达方式.
- 调整某个控制点只会造成 曲线局部的变化 而不会导致贝塞尔曲线 “牵一发而动全身” 的效果, 方便在对曲线建模时修改和编辑.
注意:
-
和贝塞尔曲线不同, B-样条曲线 不被要求必须通过任何一个控制点.
-
和贝塞尔曲线相同, B-样条曲线同样受由控制点围成的区域 (也就是 凸包,
Convex Hull) 的限制, 不能超出这个区域.
在本课程中, 我们考虑 三次B-样条曲线, 所使用的 三次B样条基 如下图所示:
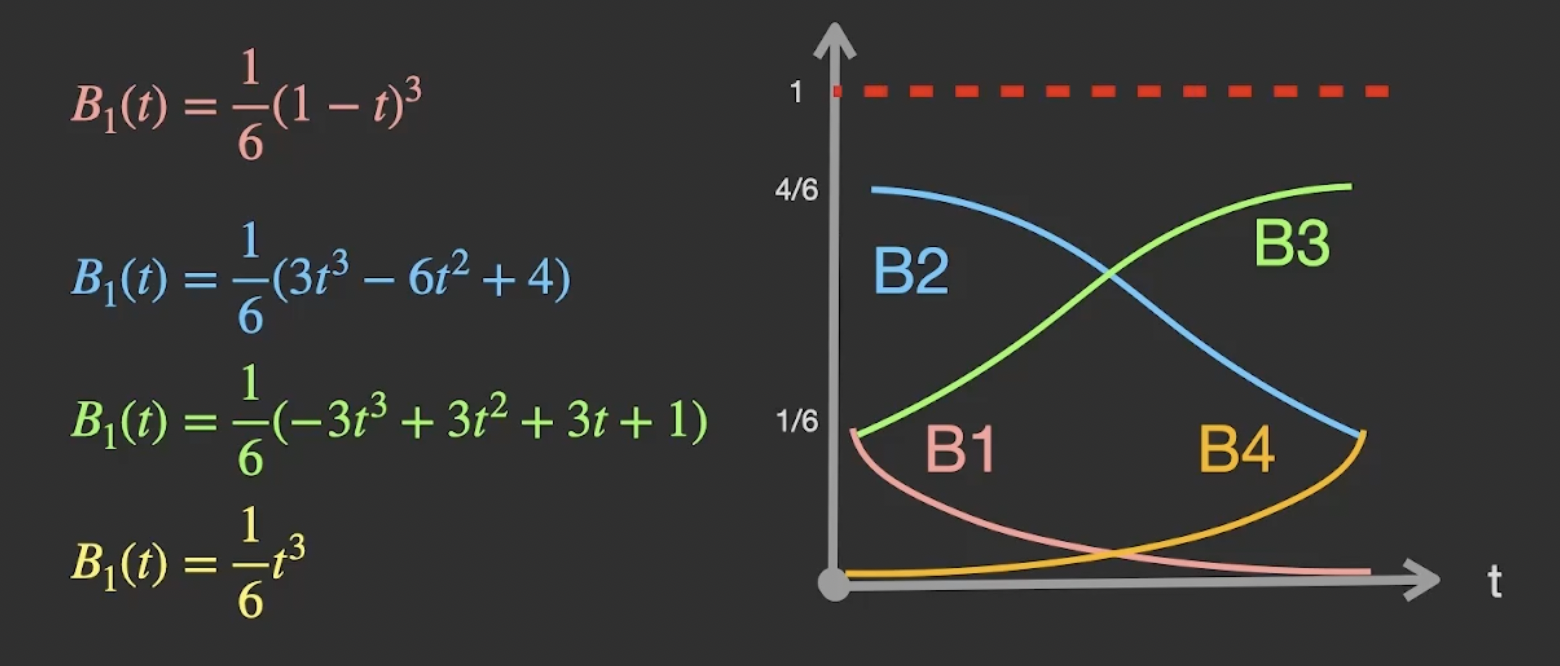
它和上面提到的, 伯恩斯坦基同样具有 单位分解 (Partition of Unity) 性质.
注意此处四种颜色不同的文字分别代表四个样条基 $B_1, B_2, B_3, B_4$, 公式里的下标全写成 $B_1$ 了.
4.1 B-样条曲线表示和贝塞尔曲线表示的互相转换
由贝塞尔曲线的矩阵表示所启发, 我们可以相应推出贝塞尔曲线的矩阵表示:

我们可以从 由给定的四个顶点作为控制点 的 B-样条曲线 的完全展开式开始反推出B-样条曲线的系数矩阵 $B_{\text{Spline}}$:
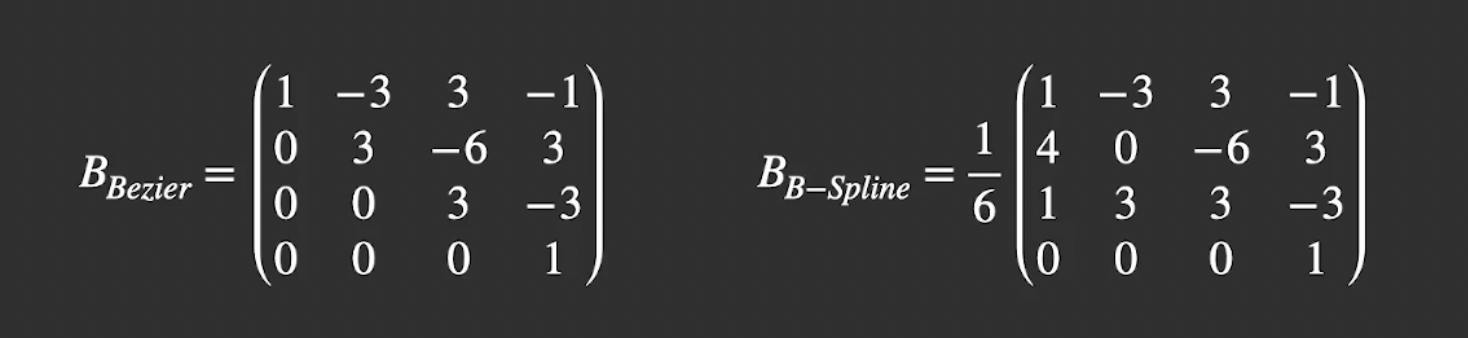
随后只需要进行一些简单的矩阵运算就可以得到下面的结果:
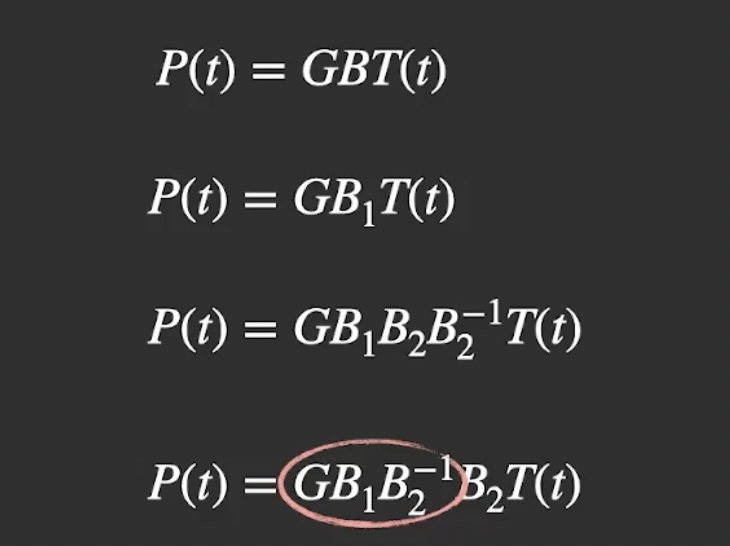
此处的目标是: 已知用贝塞尔曲线表示法所表示的曲线可以写为上图中第一行的形式, 假设给定曲线的贝塞尔表示法如第二行公式所示, 该曲线的B-样条曲线的参数矩阵记为 $B_2$, 问要通过什么样的矩阵运算将其转换为如
\[P(t) = GB_2T(t)\]的形式. (给的slides这里计算是有问题的, 不符合矩阵运算不满足交换律的性质. 倒数第二行需改为 $P(t) = GB_1B_2^{-1}B_2T(t)$.)
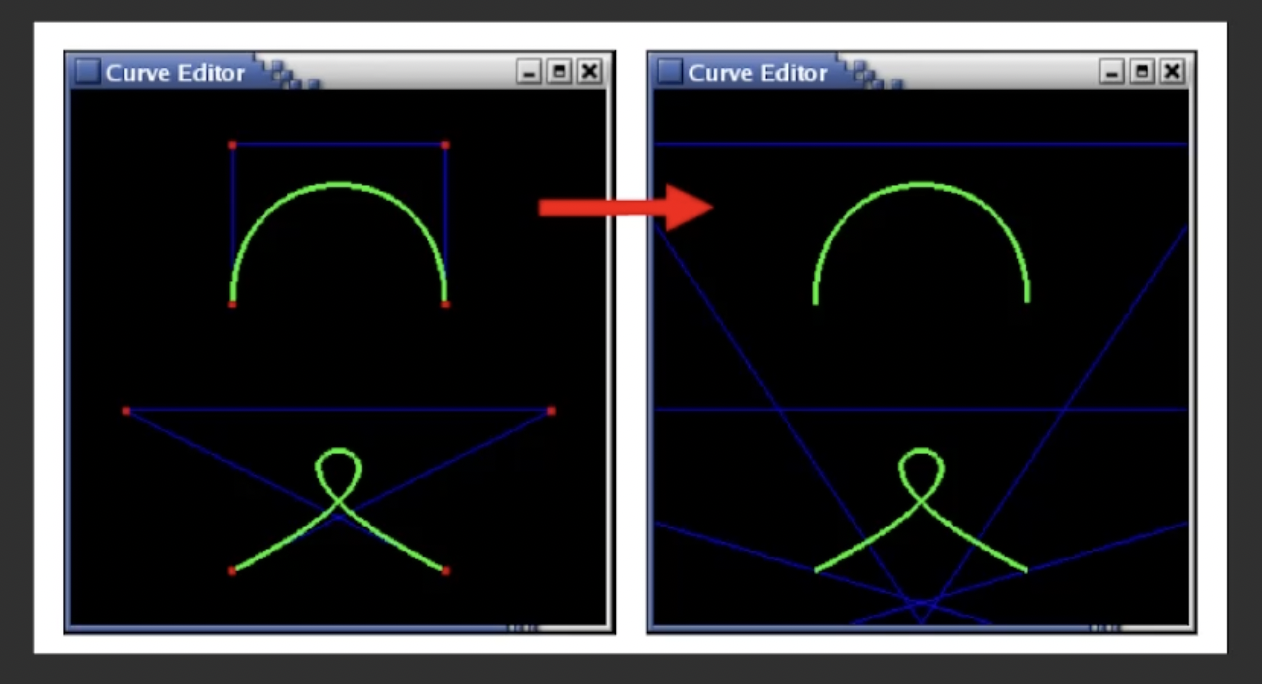
我们也称更改曲线表示法的操作为 Regrouping. 一条经过 Regrouping 的曲线如下图所示. 可看出 曲线的形状保持如初, 但 它的控制点发生了改变.
4.2 非均匀有理样条 NURBS (Non-Uniform Rational B-Spline)
非均匀有理样条也称 非均匀有理B-样条曲线, 为了 更精确地表示曲面, 尤其是圆锥截面 而引入. 本课程在此处未作更详细的介绍.
