COMP26120 算法期末总复习
Quiz
Week1: Graph Traverse and Topological Sorting

($\uparrow$ 注意存储图的两种方式: 空间占用小但删除边和检测边时间复杂度为 $O(\vert v \vert)$ 的邻接列表, 和只有检测后继边时间复杂度为 $O(\vert v \vert)$ 但空间占用为 $O(\vert v^2 \vert)$的邻接矩阵法, 后者适合边多的图, 前者适合边稀疏的图)
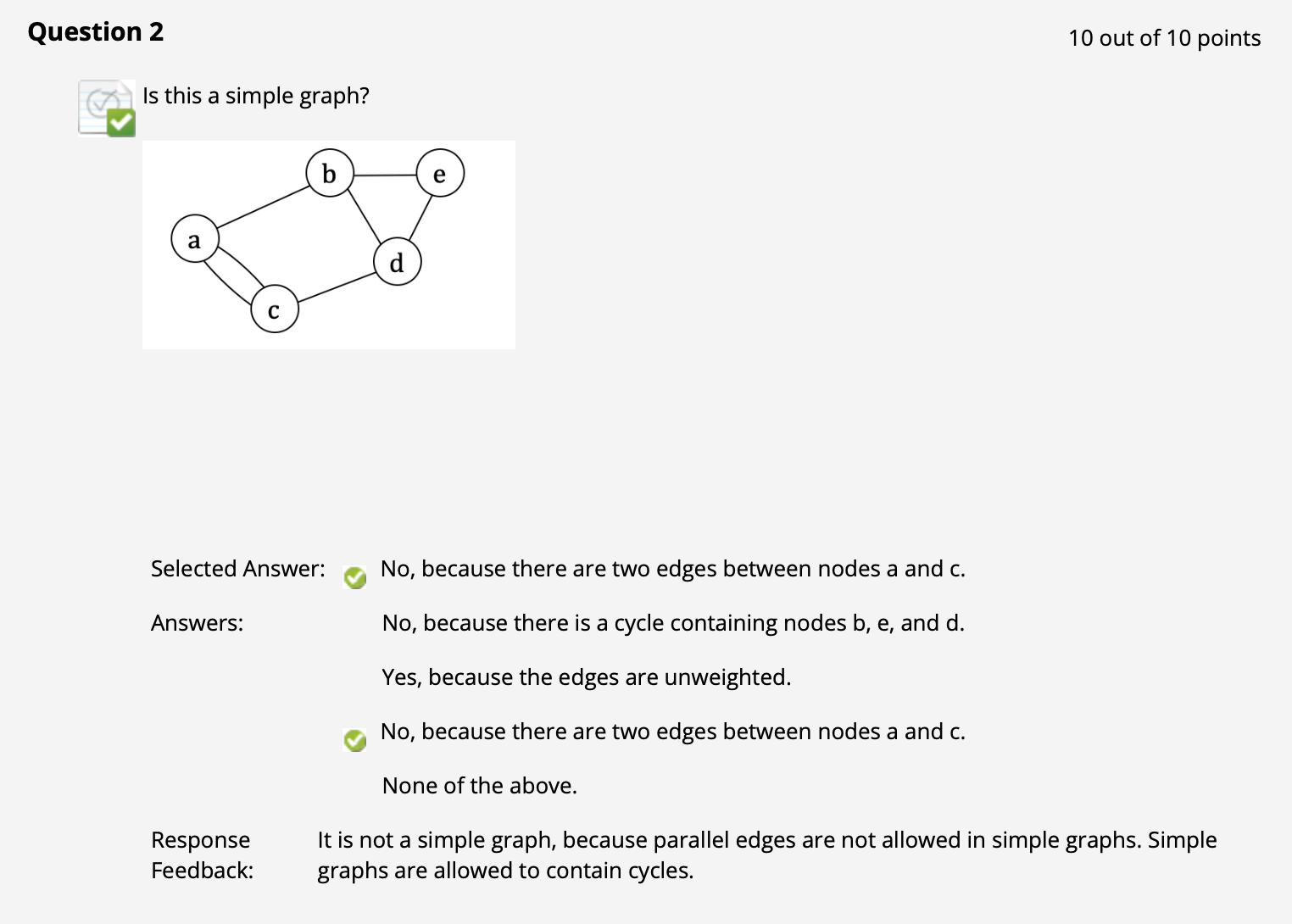
($\uparrow$ 注意简单图的定义: 就是没有重复的边的图, 显然上面的图有圈)
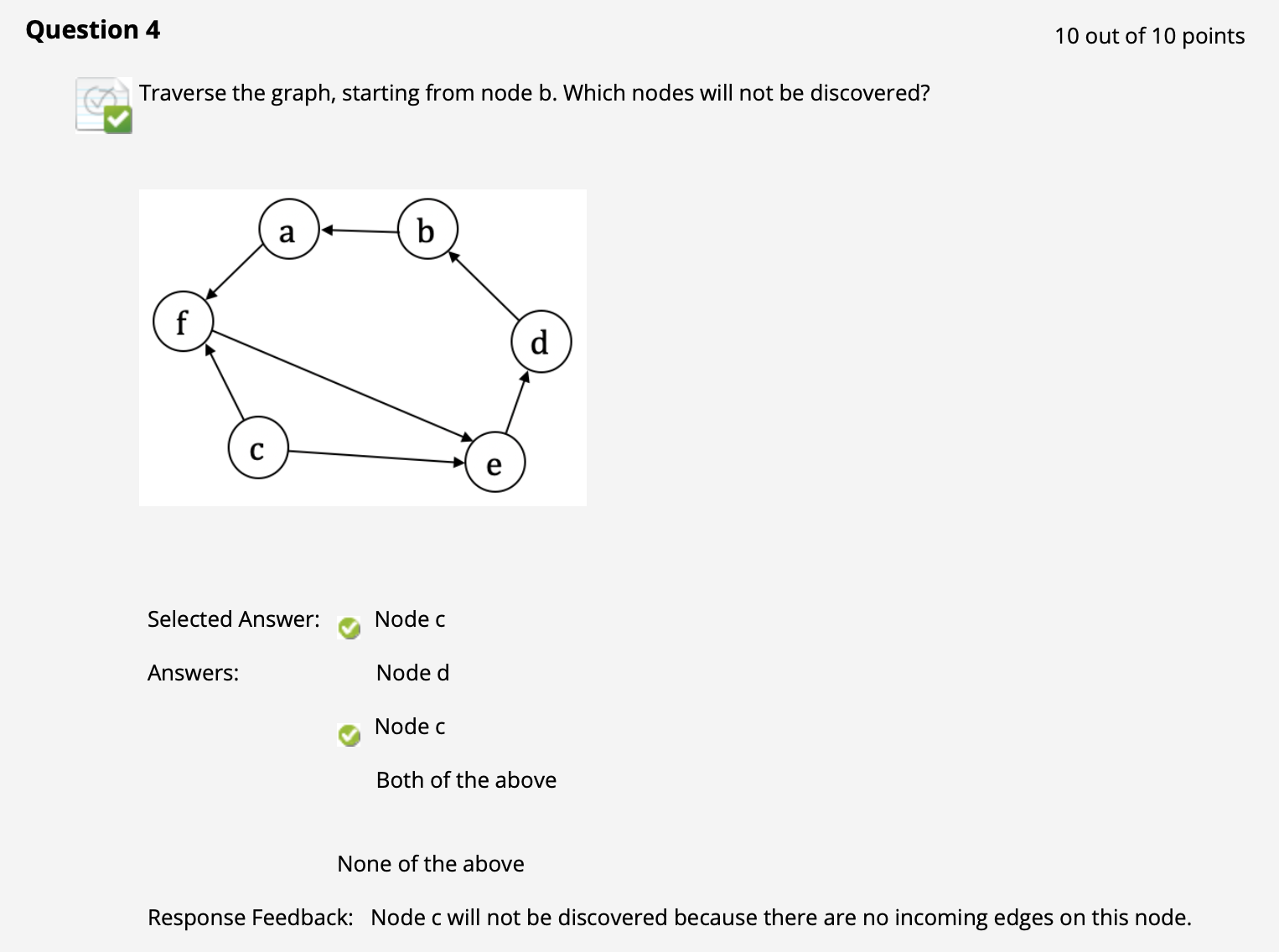
($\uparrow$ 如果有向图中的任何节点 既没有任何父节点 又 不是初始节点, 则它永远不可达)

($\uparrow$ 别脑抽把堆和栈搞混了. 清楚的记忆方式是: 假设检查到新节点时总是将新节点放到一个列表末尾, 如果把列表当作栈处理则总是弹出刚刚插入的新节点 (因此深度优先), 反之则优先弹出旧节点 (因此广度优先).)

($\uparrow$ 深度优先不会搜索已发现过的节点)

($\uparrow$ 注意拓扑排序的执行过程: 先执行 对有向图 的含圈检测, 只有确定图中无圈后才会进一步执行 DFS 得到排序结果)
Week2: Shortest Path


($\uparrow$ 基于 BFS 的最短路径寻觅算法用 队列 存储 每个节点的深度最低的父节点.)

($\uparrow$ 所以某种意义上说, 有权图中任意两点的路径具有唯一性)
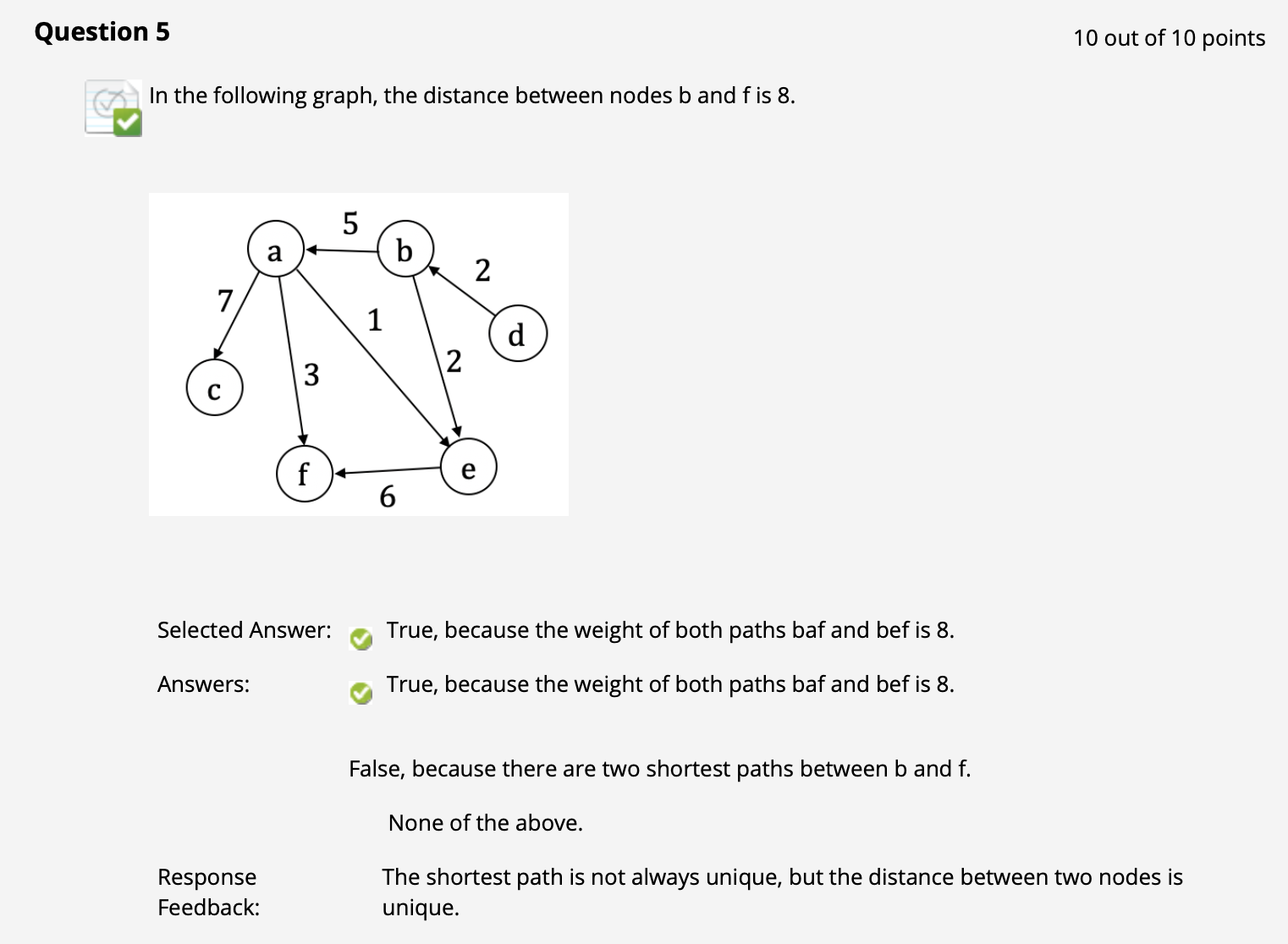
($\uparrow$ 最短路径 可以不唯一.)

($\uparrow$ 注意 Bellman-Ford 算法的 适用范围: 只要图中 不存在总权重为负的圈, 那么不管这个图长啥样都适用该算法.)

($\uparrow$ 这种题都做错的话说明 Bellman-Ford 算法的基本原理都没搞懂, 罚你留级)

($\uparrow$ 注意 Bellman-Ford 算法松弛循环的最大运行次数, Worst Case: 图退化为路径, 以及该算法的实际时间复杂度 $O(\vert V \vert \cdot \vert E \vert)$. 原因: 因为还要同时检查图里是否有负权圈, 所以增加了时间复杂度)

($\uparrow$ 回顾解释 Bellman-Ford 算法正确性时对循环不变量的构造)
Week3: Dijkstra 和 A*

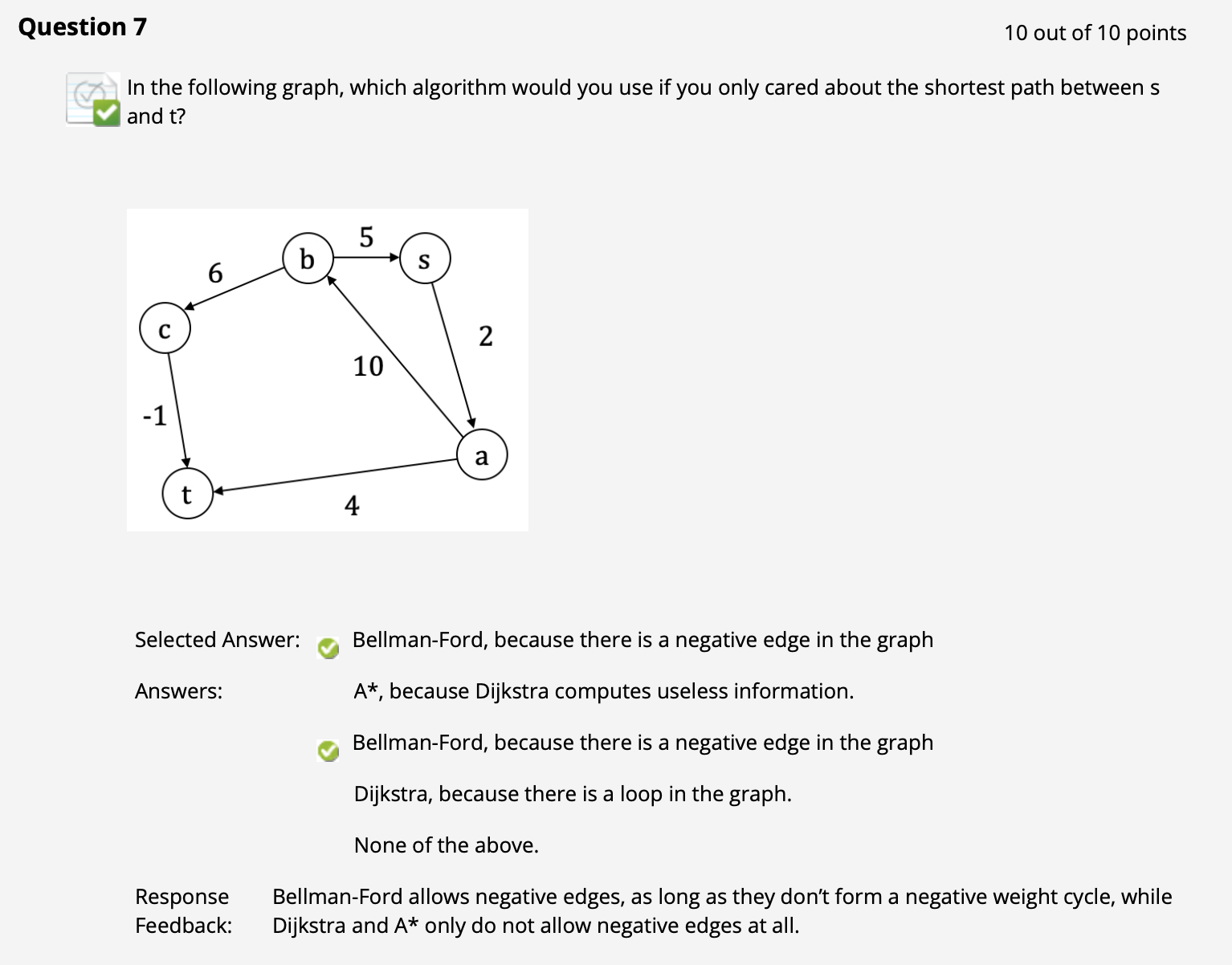
($\uparrow$ 如果做错的话请再次回顾三种计算有权图最短路径算法的适用范围, 这个问题已经在前面的笔记里着重强调多次了, 还不会的话罚你明年重修)

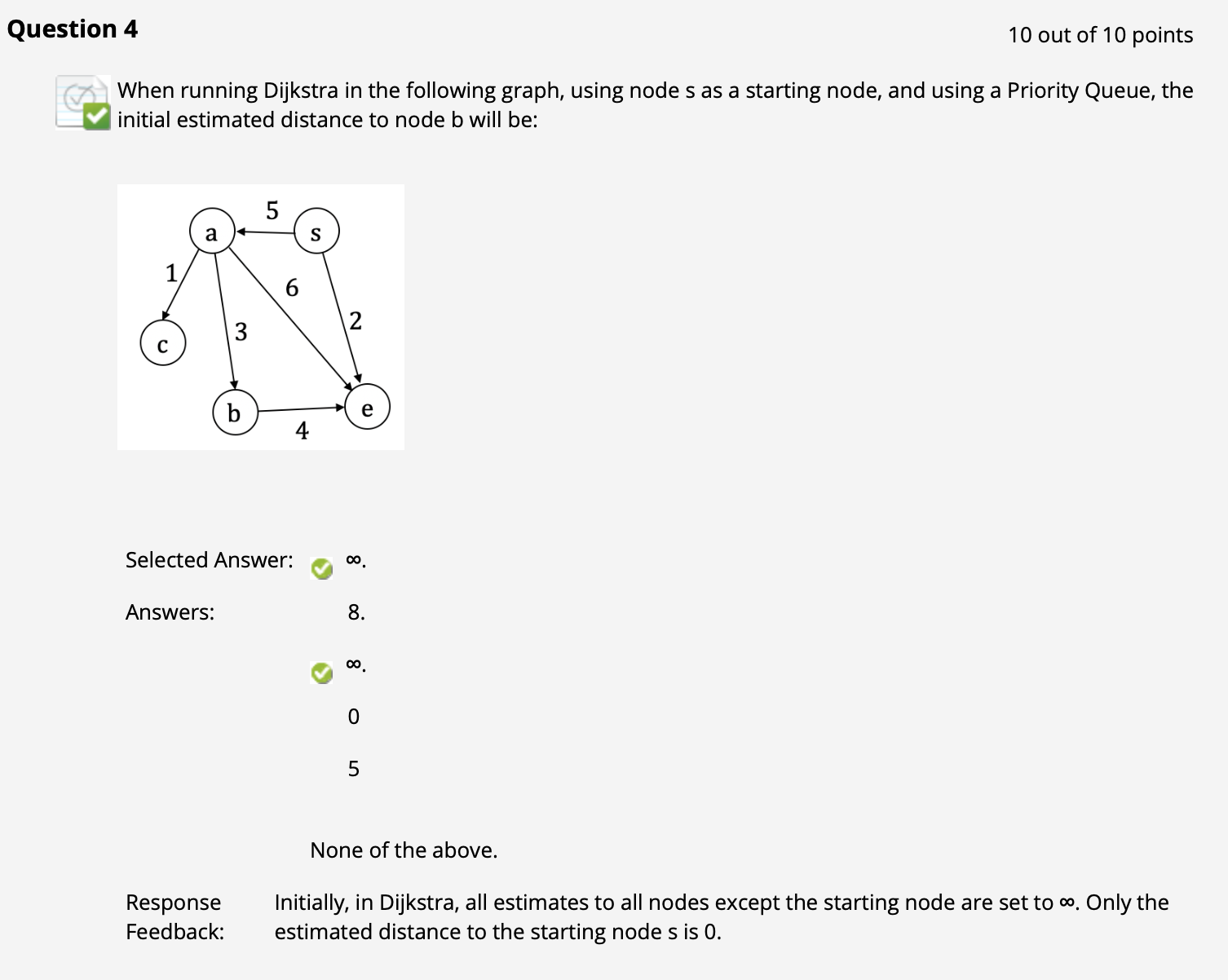
($\uparrow$ 注意 Dijkstra 算法对所有节点目标路径权重的估计逻辑和 Bellman-Ford 算法是一样的; 同时回顾定义: 如果真的有某条 “边” 在 边的 权重矩阵中对应值为 $\infty$, 说明 对应两个节点之间实际上不相连. )

($\uparrow$ 这样可以优先找路径权重估计相对最小的点, 比在 D (Discovered Nodes) 中盲目瞎猜可以更快地先找到真正的最短路径)

($\uparrow$ 该题不难, 但想象一下新场景: 如果 w(a,b)=3.75, w(s, c)=3.5, 此时该选谁?)

($\uparrow$ 这个性质是和 A* 结合启发式的贪心剪枝特征结合的, 正是由于结合了启发式, A* 可以安全地确保只要计算到目标节点的松弛时, 所计算出的一定是最优解.)


($\uparrow$ Dijkstra 算法和 A* 算法的优化原理与各自的假设必须理解得非常清楚: 二者实际上都是基于 Bellman-Ford 发展而来的产物, 前者的性能优化基于 “单源最短路径的求解具有贪心性质: 最优解的局部解必也是最优局部解” 这一假设; 而后者在 Dijkstra 基础上引入了启发式函数 H() 估计每个节点到目标节点的距离用以实现进一步剪枝)

($\uparrow$ 回顾课上介绍 “启发单调性” 时展示的三角形关系可知, 满足启发单调性的启发函数绝不会 overestimate; 也可回忆课上对这部分内容介绍时的逻辑顺序: 启发单调性实际上是比可启发性更强的性质)
Week4: 最小生成树

($\uparrow$ 生成树的基本定义)

($\uparrow$ 关于贪心算法的性质可以回顾 Lab5 中对 $0-1$ 背包问题的贪心算法实现)
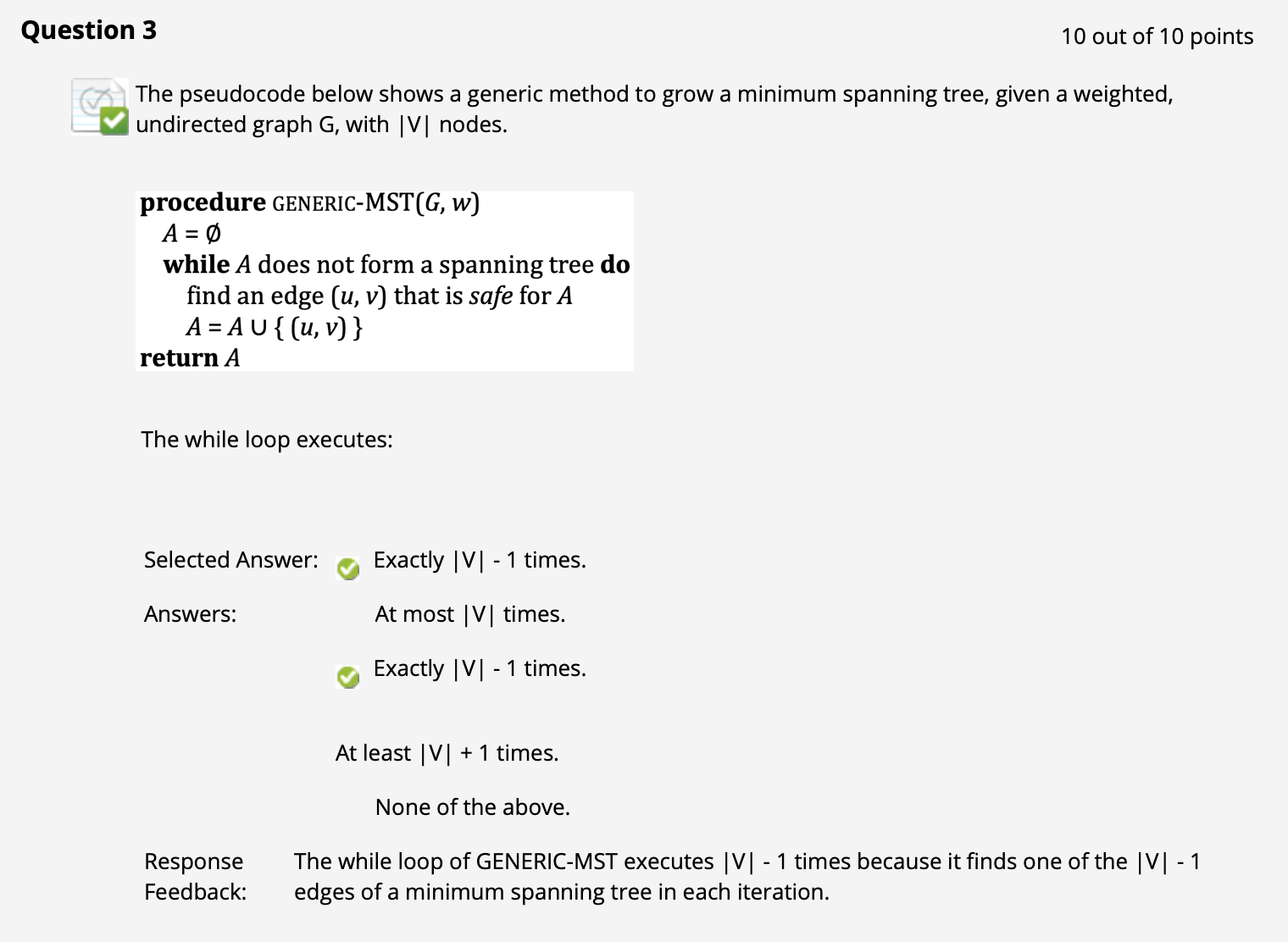
($\uparrow$ 通用贪心算法每次循环都让子 MST 多连接一个图中的点, a.k.a. 多一条边, 因此需要循环 $\vert V\vert -1$ 次才能包含图中所有点)
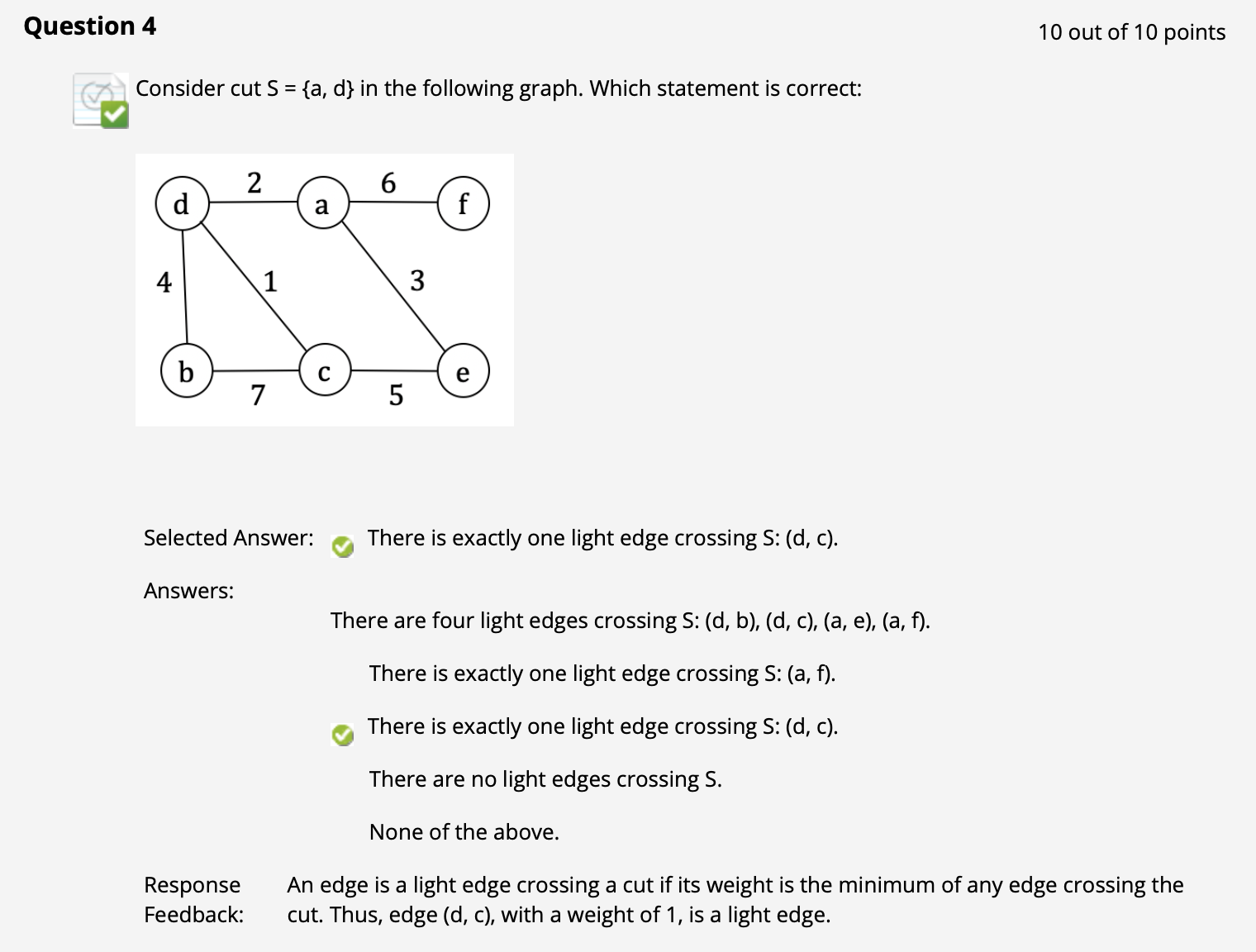
($\uparrow$ 这个 cut 一定要经过边 ad, 在此基础上它可以经过任意其他边. 显然在这里它可以经过权重最小的边 cd.)
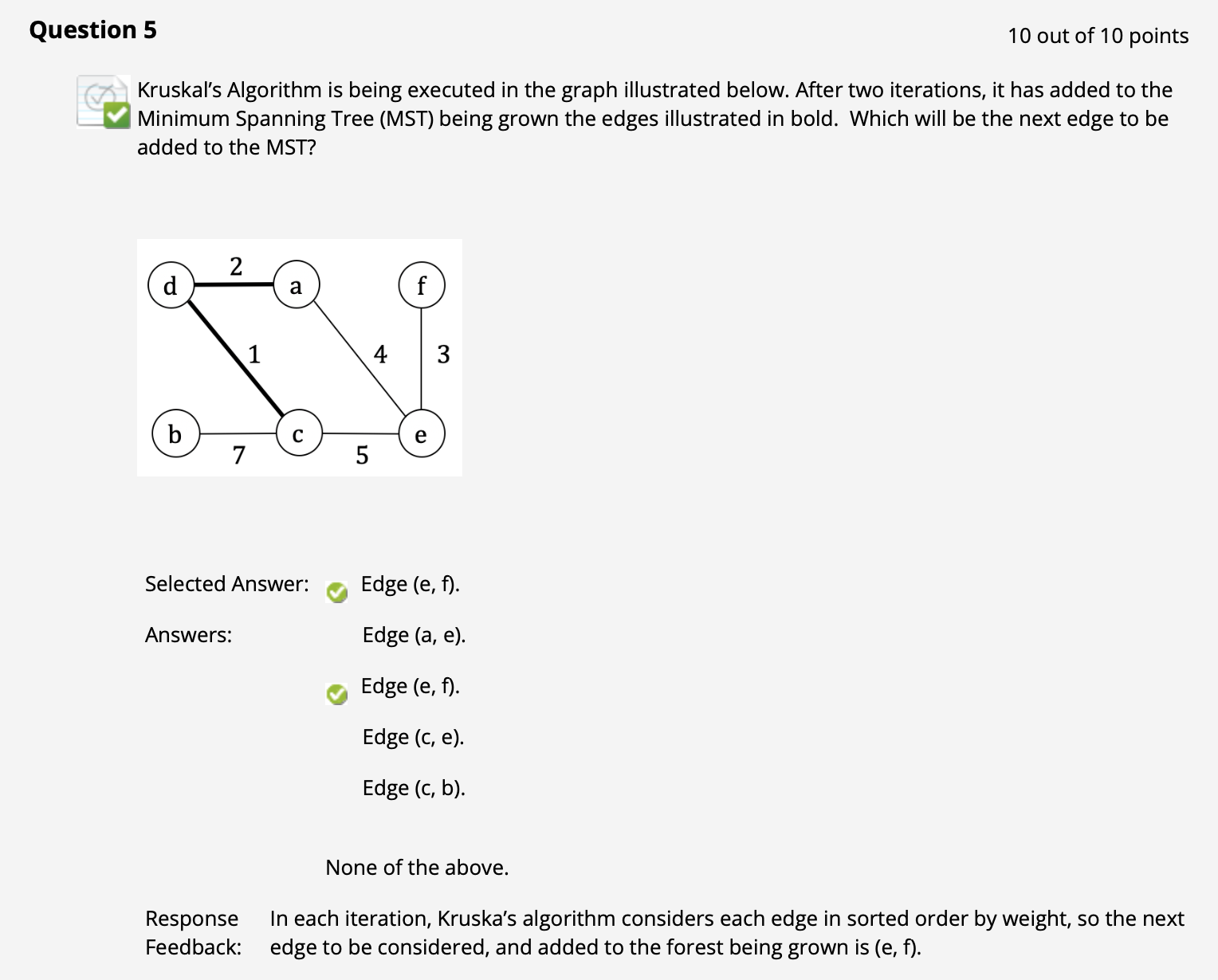
($\uparrow$ 回顾 Kruskal 算法的基本思路, 它是 基于任何边的权重 的, 添加的边可能当前并不和子 MST 连通, 但最终总会连通. 因此它会考虑剩下的全局权重最小边, 必然选择 ef.)
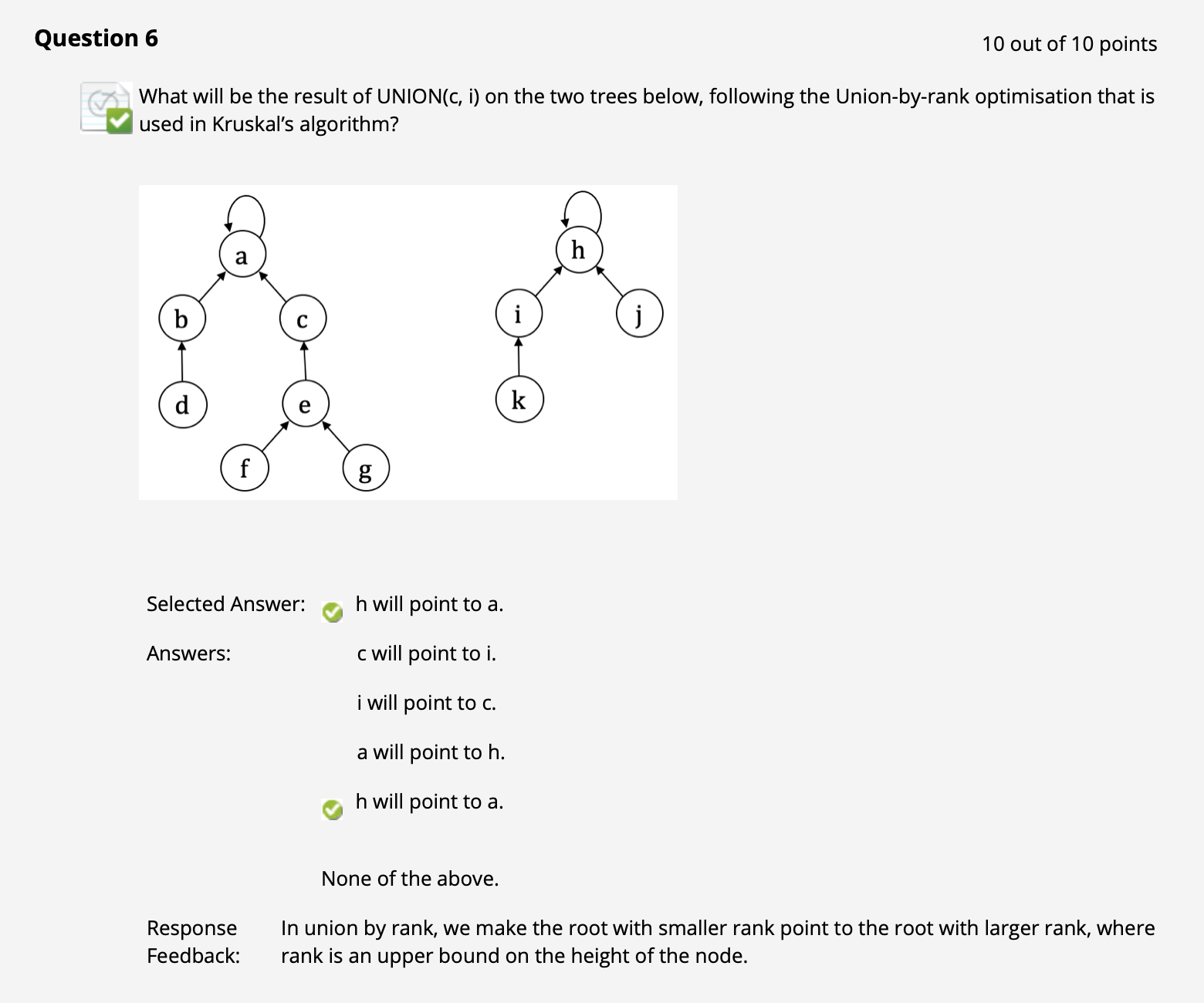
($\uparrow$ 注意 Union By Rank 的概念. 所谓的 Rank 实际上指的是树的深度, 浅的树的根节点直接挂靠到更深的树的根节点上.)
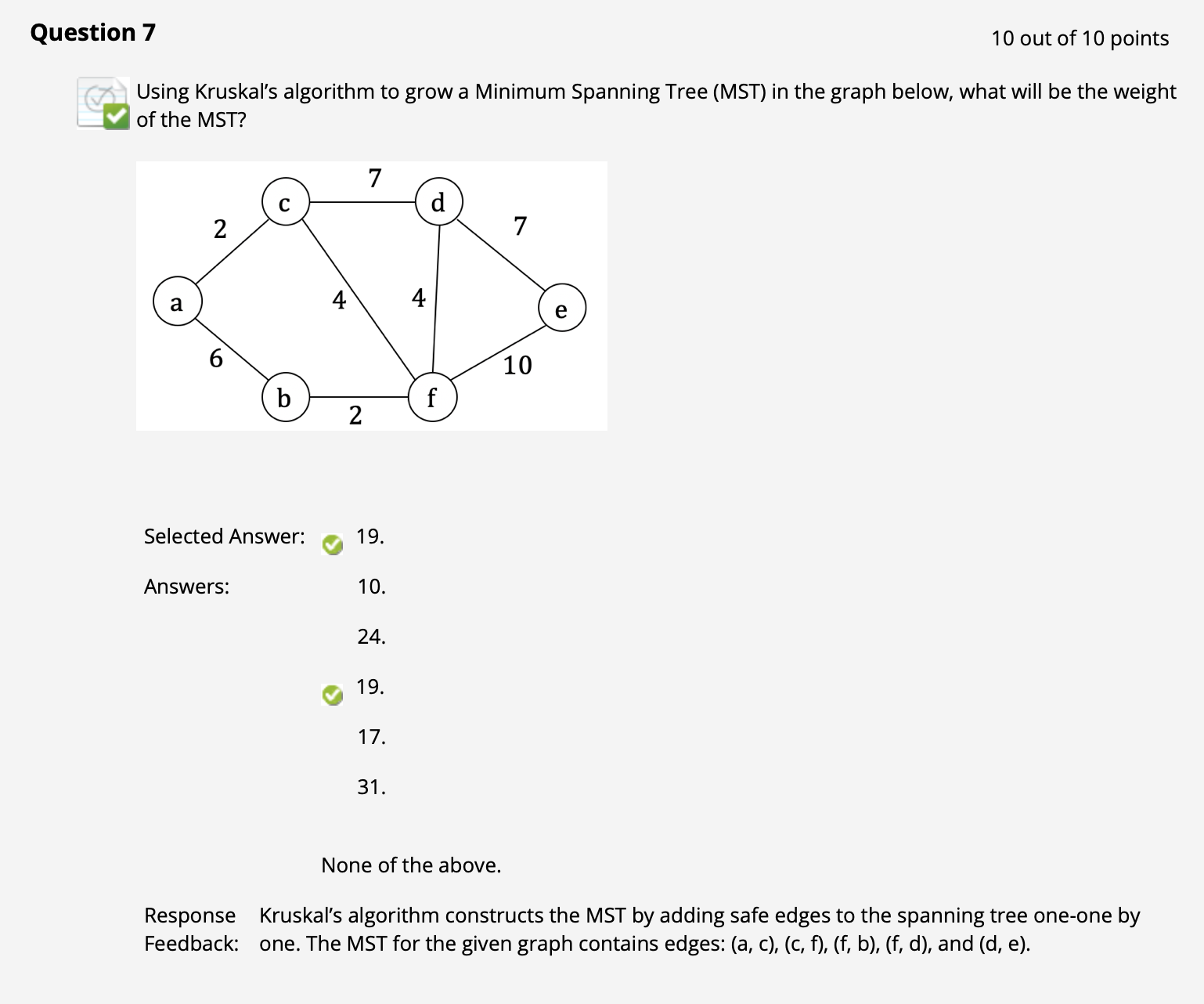
($\uparrow$ 此处借这个例子解释一下 Kruskal 算法的执行过程):
首先生成 $6$ 个并查集和一个空的子 MST, 记为 $A$. 然后考虑全局权重最小边, 不妨假设在 ac 和 bf 中随机选择了 bf.
然后监测到 b 和 f 所在的并查集代表元不同, 因此合并. 这里因为 b 和 f 的并查集深度相同所以在 Union By Rank 规则下怎么合并都行, 不妨假设 b 挂靠到了 f 上. 此时将这条最短边 bf 加入 $A$ 中.
然后在剩下的边中找剩下的最短边, 挑到 ac. 重复同样的过程, a 和 c 挂靠在一起, 新的边ac 被加入 $A$.
再然后用相同的方式可以随机选择 cf 和 df, 为了偷懒少打字解释这里假设随机选到了 cf. 由此我们就将 a, c, b, f 合四为一放在同一个并查集里, cf 被加入 $A$ 中.
进一步地就剩下了 df. 在这一步之后 d 也被扔进 acbf 集中营, df 加入 $A$ 中.
然后按照规则我们应该在剩余的边里选 ab. 由于已知 acbfd 此时都挤在同一个并查集里, 所以根据规则这条边不能加, 扔掉.
再然后我们可以用同样的原因扔掉 cd, 把 de 加入 $A$. 此时只剩下唯一的一个并查集, 其中就已经全部包含了图的所有顶点.
此时回头看我们的 $A$, 知道包含边 bf, ac, cf, fd, de, 权重总和为 $19$.

($\uparrow$ 此处借此机会解释一下 Prims 算法的运作过程):
我们拿到的是 Prims 算法运作的中间状态, 此时子树 A 已经包含 连通 的三条边 ac, ab 和 bf.
然后考虑剩下的边中 和 A 相连, 至少有一个顶点不在 A 中, 而且权重最小 的边, 显然排除掉不满足规则的 cf 之后最合适的是 fd.
和 Kruskal 的 “早有预谋” 不同, Prims 算法就是这样一步步地逐渐生成 A 的. Kruskal 算法每一步扔进 A 的边都是 “不一定和当前子树连接, 但最终必会相连” 的边, 而 Prims 每次新增的边都是和当前子树连接的.

($\uparrow$ 因此不难看出, 其实这个错误选项所描述的更像是 Kruskal 算法)
Week5: 线性规划

($\uparrow$ 务必注意线性规划中 目标函数 (Objective Function) 和 约束函数 (Constraint Function) 的区别! 这里要我们找的是目标函数, 不是约束函数.)

($\uparrow$ 虽然反直觉, 但是考虑到如果要 Minimise 则无意义的 $0$ 就一定是解. 具体的解释看高亮部分)

($\uparrow$ 这也会是下一章单纯形法原理的一部分)


($\uparrow$ 注意在线性规划的标准形式下目标函数总是要被取最大值的, 所有的约束要表示为 “小于等于” 形式)

($\uparrow$ 只要可被表示为 线性的 包含 小于等于号 的形式, 它就是合法约束)

($\uparrow$ 想什么呢, 你甚至都不是线性的…)
Week6: 单纯形法


($\uparrow$ 注意 “基础变量”, “松弛变量” 和 “基础解” 的定义)
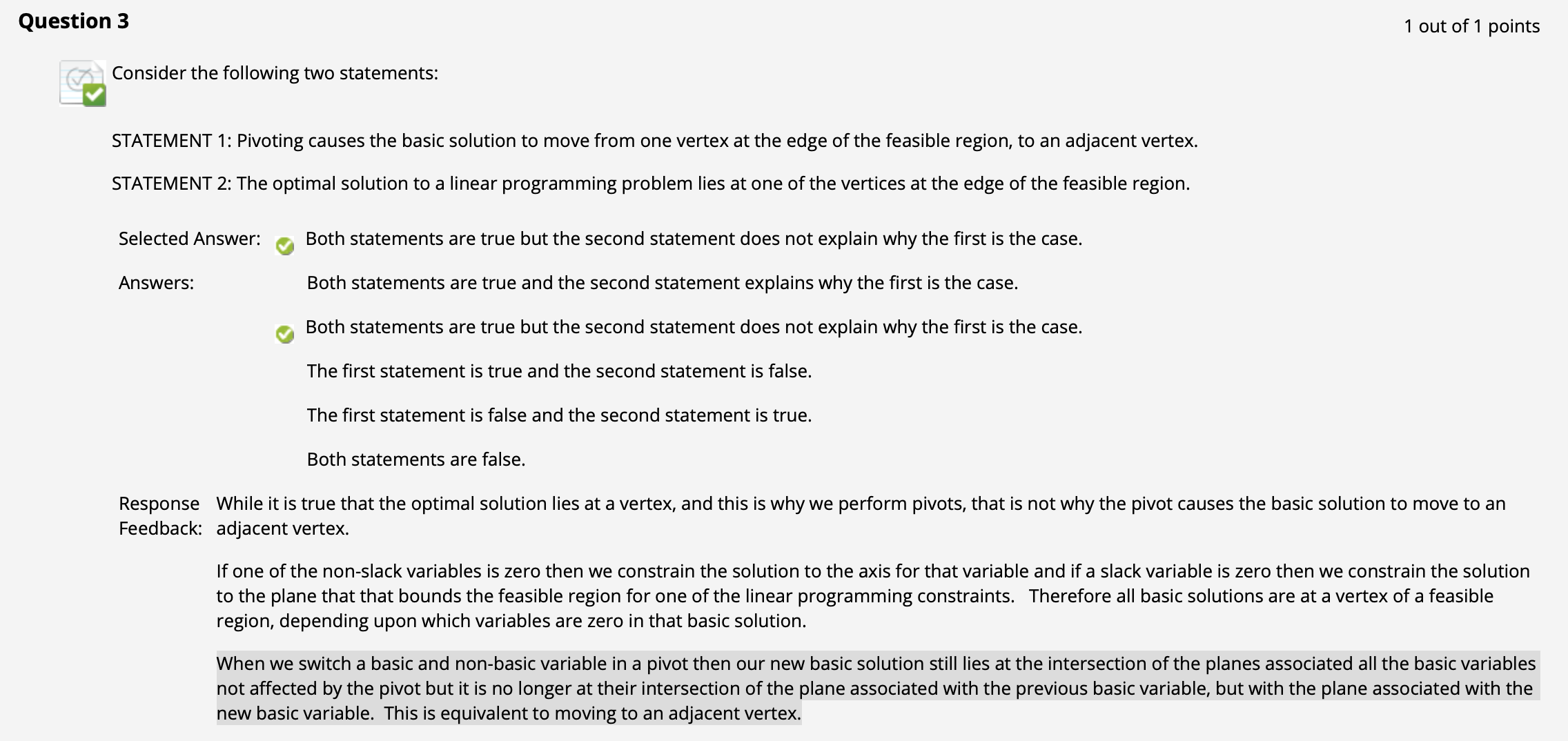
( $\uparrow$ 注意高亮部分对 “为何 Pivoting 等价于从一个可行解移动到邻接的另一个可行解” 的解释.)

( $\uparrow$ 注意运用课上提到的, 选择 Pivot 行的 Heuristic 规则.)


( $\uparrow$ 检查 unbounded 问题时都需要考虑全面.)

( $\uparrow$ 注意 Degeneracy 的概念: “A pivot in the Simplex Method is said to be degenerate when it doesn’t change the basic solution”.)

( $\uparrow$ 注意对 Simplex 算法最高执行次数的分析)
Week7: 高级单纯形法
先连着看几个 同类型问题:




($\uparrow$ 注意 leaving variable 的选择顺序: 若 entering variable列参数不全为负则问题有 bound; 然后检查 pivot 是否有 $0$ 值, 如果有 $0$ 值的话再检查 entering variable 列的系数: 如果有正系数且对应 pivot 为 $0$, 则选 pivot 为 $0$ 中 正系数最小 的; 如果只有负系数则和原来一样考虑使 pivot 非负且最小的行.)

($\uparrow$ 其实不一定非得选 $a_1$, 只要 leaving variable 为 $s_1$, 通过 pivoting 能把问题转换为常规形态可解问题的话选啥都行, 但在这里选 a_1 的话方便计算, 好做)

($\uparrow$ 只要看到某列系数全负直接扔掉)
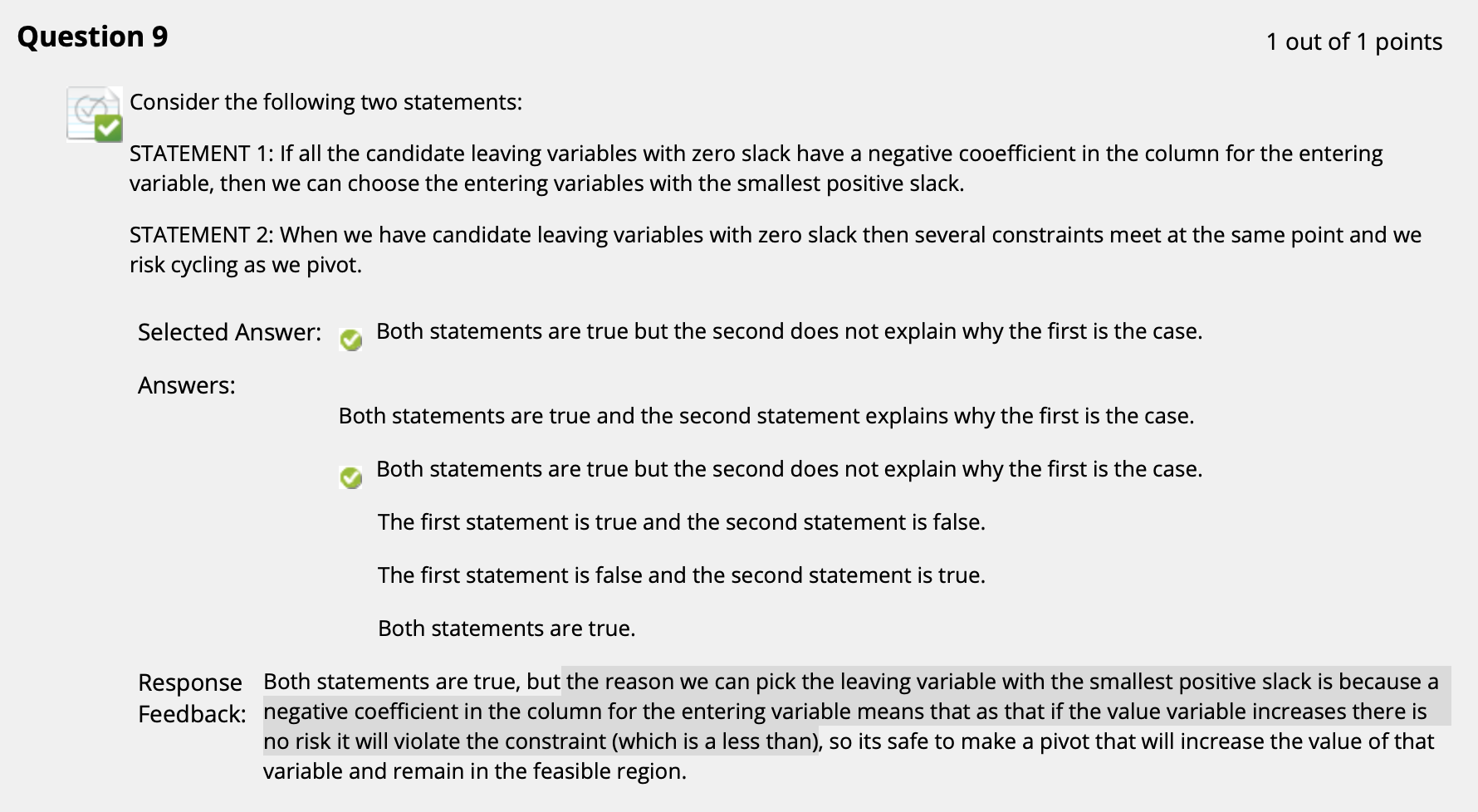
($\uparrow$ 解释的很清楚了, 自己看)
Week8: El Gamel

($\uparrow$ 实际上, 从数论知识可知任何素数 $p$ 都有 $\phi(\phi(p))$ 个原根, 因此在这里 $11$ 的原根有 $4$ 个.)

($\uparrow$ 这里其实无需考虑太多, 首先 $2$ 和 $8$ 就不互素).
此处介绍一个 快速判断给定数 $g$ 是否为某个素数 $m$ 的原根的方法:
若 $g$ 是 素数 $m$ 的原根, 则它必然满足;
- $0 \leqslant g < m$
- $\text{gcd(g, m) = 1}$
-
考虑 $\phi(m)$ 中的所有 质因子, 对任何其质因子 $q$, 均有
\[g^{\frac{\phi(m))}{q}} \not \equiv 1 ~\text{mod}~ p.\]


($\uparrow$ 这个…没啥好说的, 背吧…)

($\uparrow$ 回顾最后一章中介绍的 伪线性时间复杂度 算法的定义以及素数检测章节中 伪线性的朴素素数检测法, 可知这个函数才是计算困难度理论下的真正的线性函数: 计算时间的增长关于输入位数长度的增长是线性的.)

($\uparrow$ 回顾 “单向加密” 原则)

($\uparrow$ 此处注意联系 原根 的定义理解. 实际上对于任何一个合法的 El Gamel 加密公钥, 只要前两个值分别是: 素数 $p$, 以及 $p$ 的原根, a.k.a. $\mathbb{Z}_{p}$ 的生成元, 则第三个数 $y$ 只要比 $p$ 小就行, 因为总存在一个位于 $p$ 的简化剩余系中的 $x$ 使 $g^{x} ~ \text{mod} ~ p \equiv y$.)

($\uparrow$ 此处第一个 Statement 成立的原因实际上是和 El Gamel 加密法公钥和私钥精密的构造方式直接相关的)
Week9: 素数检测

($\uparrow$ 抓住基本定义: 对二进制形式位长为 $n$ 的数 $x$ 而言,$\pi(x)) \approx \frac{x}{\ln(2^n)}$, 因此平均要测 $\ln(2^n)$ 次.)

($\uparrow$ 二进制形式位长为 $n$ 的数大小最多不超过 $2^n$, 而基本除法从该数的平方根开始反推到 $1$, 因此最多执行不超过 $2^{\frac{n}{2}}$ 次.)


($\uparrow$ 两个同类问题, 注意对随机素数判定法循环体中循环次数 $t$ 的计算方式和推导原理, 记住计算完后要向上取整.)

($\uparrow$ 经典问题, 注意费马小定理的重要条件: 可正确判定 $x$ 为素数的必要不充分条件是 $x$ 还需要和 $n$ 互素.)

($\uparrow$ 回顾我们在介绍 Rabin-Miller 素数判定法时引入的结论: 当且仅当 $n$ 为素数时, 对于 $x^2 ~\equiv~1~\text{mod} (n)$ 有 $x ~\equiv~ \pm 1 ~\text{mod}~n$. 在本题中对 $x$ 的取值范围限定了 $x$ 绝不可能满足 $x ~\equiv~ \pm 1 ~\text{mod}~n$, 因此 $x$ 必不为素数.)

($\uparrow$ 此处对算法运行时间复杂度的估计需要结合上一章中对快速模幂算法的时间复杂度 $O(\log(n))$.)
Week10: (不) 可计算性

($\uparrow$ 基础的定义问题, 包含关系弄反了)

($\uparrow$ 这个问题的答案本质上是 P != NP? 的答案. 但是 P != NP? 有答案吗? 想想量子计算机.)

($\uparrow$ 对 NP 问题 Certificate 检测的时间复杂度必须是 关于输入长度呈多项式级 的.)

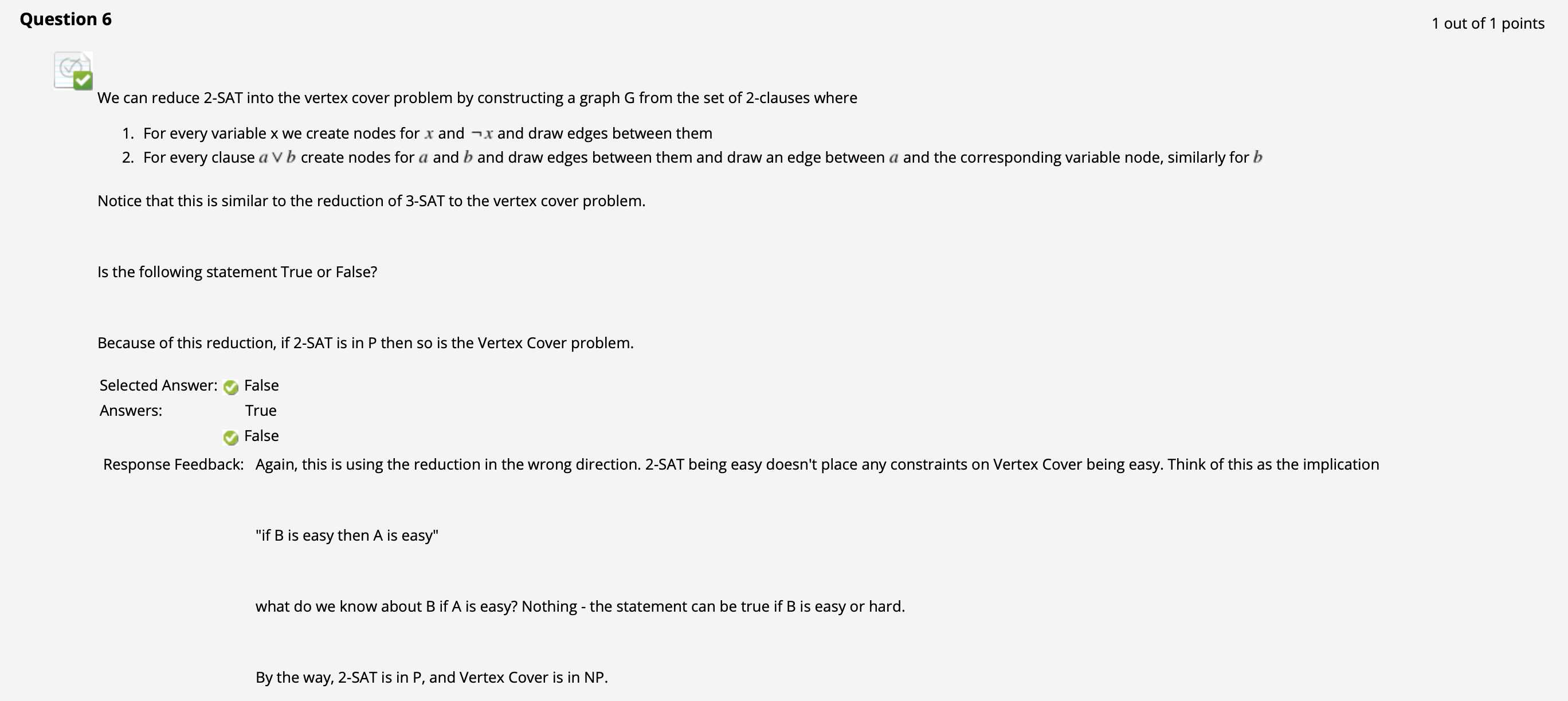
($\uparrow$ 记住偏序关系 $\leqslant_{P}$ 的构造顺序: 若$A$ 可被多项式时间内简化为 $B$, 则计算困难度关系为 $A \leqslant_{P} B$.)

($\uparrow$ 记住: 对于 NP 问题, 其 certificate 的长度和检验 certificae 消耗的时间都要与其 输入长度而非输入数值大小 的变化呈 多项式 级别的关系.)
Week11: 展示 NP-Completeness

($\uparrow$ 对于 $k \geqslant 3$, k-SAT 问题都是 NP-Complete 的.)

($\uparrow$ 搭建逻辑门电路硬编码验证函数 $A(w, c)$, 所有了解从 NP 向 Circuit-SAT 简化的人都应该对这个结论印象深刻)

($\uparrow$ 注意熟悉不同图相关 NP-Complete 问题的定义)
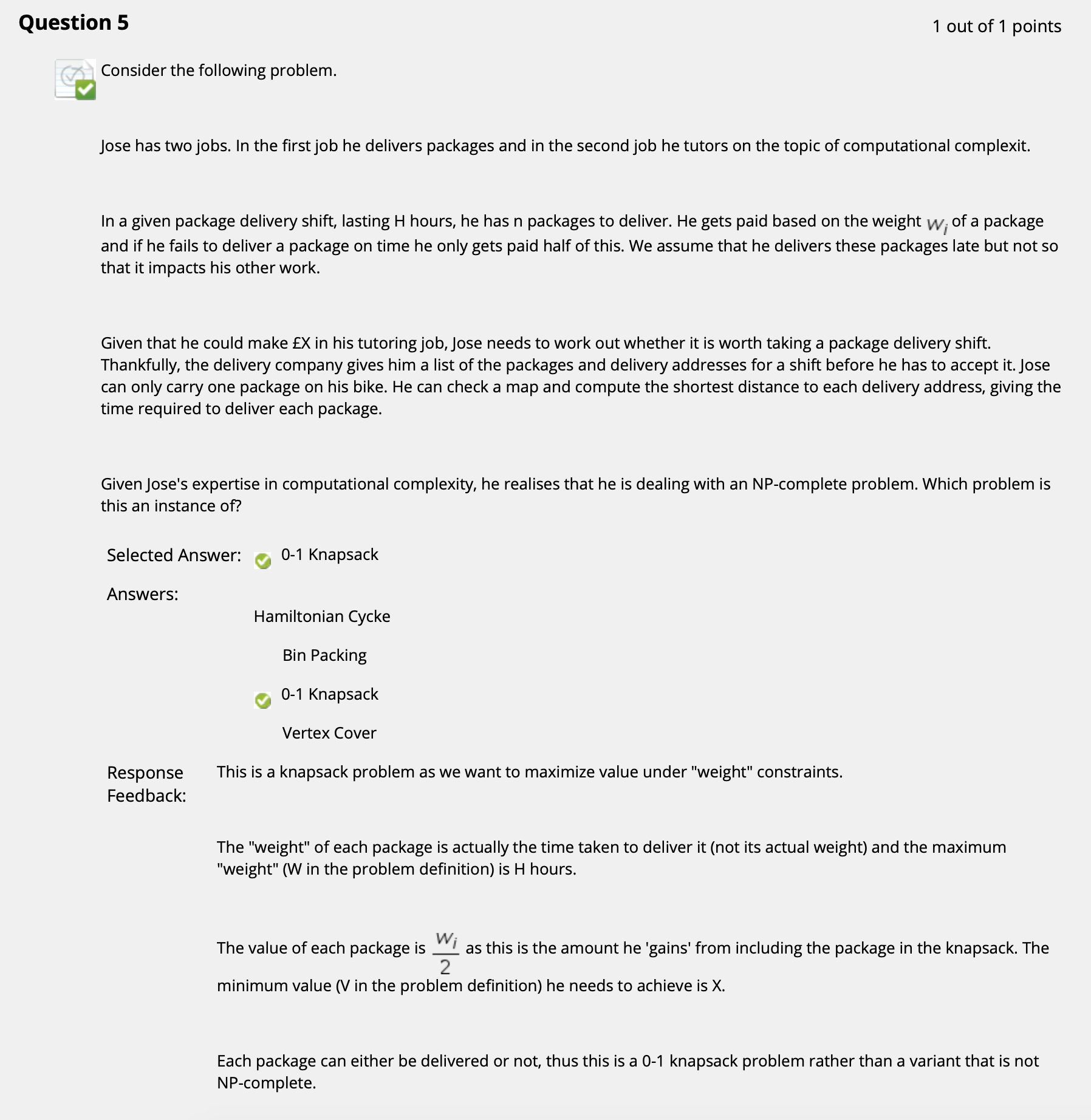
($\uparrow$ 仔细观察会发现这其实是 $0-1$ 背包问题, 由于没有分划因此问题和 Bin Packing 无关, 由于该问题不涉及任何与图相关的语义 (不排除一开始看到地图会自然联想到旅行商问题, 但完整看一遍题目描述会发现主角并不能规划路线) 因此可排除出正确结果.)

($\uparrow$ 这里的定义解释的已经很清楚了, 有时间的话最后一周的最后一个视频还是要看)
Past Paper

($\uparrow$ 注意图的两种表示方式使用的数据结构区别: 列表/链表和数组. 其中后者只有 successor() 查找性能为 $O(V)$.)

($\uparrow$ 对深度优先和广度优先算法而言, 若在从 Discovered 序列/栈中弹出某个节点, 检查该节点时发现了任何 已经在 Discovered 中的子顶点, 则需要将这些被新发现的顶点在 Discovered 中的顺序 更新: 删掉原来的, 然后按照题目给定的顺序放到序列/栈尾.)

($\uparrow$ 不作过多解释. 需要注意, 最基础的 MST 算法: 通用贪心算法同样是依赖 cut 的. 同时回顾 MST 的定义: 连接图中 所有 顶点的树; 最小生成树可以不唯一, 也可以压根就没有.)

($\uparrow$ 处理这类题的时候务必使用 机器时间 计算约束.)

($\uparrow$ 回忆单纯形法中选择 pivot 的两条基本规则.)

($\uparrow$ 牢记 Rabin-Miller 算法的基本原理和错误率 $q=0.25$.)

($\uparrow$ 注意 NP, NP Hard, NPC 之间的关系: NPC 是那些同时为 NP 和 NP Hard 的问题. 因此此处的包含关系无误.)

($\uparrow$ 注意 Reduce 关系有传递性.)
最后注意 Synoptic Questions 的答题要点:
- 给定问题要求提出算法类的问题需要依次回答 所使用的数据结构和算法, 以及算法设计技术, 算法本身的基本流程说明 (可以附上伪代码) 以及 复杂度分析. 每个过程都要详细说清楚, 如果涉及并查集或任何涉及并查集的算法需要一并说明并查集的实现方式: 树, 以及路径优化方式:
Path Compression. - 给定问题实现要求答出使用的算法/程序设计思想类型一类的问题需要明确回答 所使用的算法和程序设计思想, 使用循环不变量的方式证明程序的正确性 (Base Case, Step Case, Final case), 并分析说明程序的时间复杂度.
