可计算性问题

在本章中, 我们将对 可计算性问题 进行介绍. 我们将依序介绍三种 问题的复杂度类: 可使用确定性算法在 多项式时间内 被求解的问题类 P (Polynomial Time), 使用确定性算法在多项式时间内无法求解但可验证 的问题类 NP (Non-Polynomial Time), 比 NP 问题更难求解且无法确定能否在多项式时间内被验证 的问题类 NP-Hard, 以及 既是 NP 问题又是 NP-Hard 问题 的问题类 NP-Complete.、

我们还将进一步介绍可用来验证给定问题属于哪个复杂度类的基本知识和技术, 并将通过一些例子说明应用.

P, NP 和其他非确定性问题 (Intractable) 问题定义

直观定义

我们首先分别说明 P, NP, NP-Hard 的定义.

首先明确, 这些定义都是对 问题的难易程度 的描述. 在这里, 我们对问题的 “难易程度” 所下的定义就是: 解决这一问题所需要的 时间复杂度 是什么. 显然, 对于计算能力相同的硬件而言, 需要更短计算时间就可解决的问题自然相对简单; 而对人类而言, 只有在我们的认知内可接受的时间范围内能够将问题解决的算法才具有实际意义.

因此, 我们根据 时间复杂度 可将计算问题粗略的分为三类:

1. Class P: 任何可在 多项式时间内 由 确定性算法 得出结论的问题都属于 P 类问题.
2. Class NP: 任何 需要使用非确定性算法 才能在多项式时间内求解, 或 可在 多项式时间内检验解答是否正确 的问题属于 NP 问题.
3. Class NP-Hard: 难度至少和所有的 NP 问题一样难 的问题属于 NP-Hard 问题.
4. Class NP-Complete: 既属于 NP 类, 又属于 NP-Hard 类 的问题为 NP-Hard 问题.

在本课程中, 我们认为 P, NP, NP-Hard 问题之间是 包含关系:

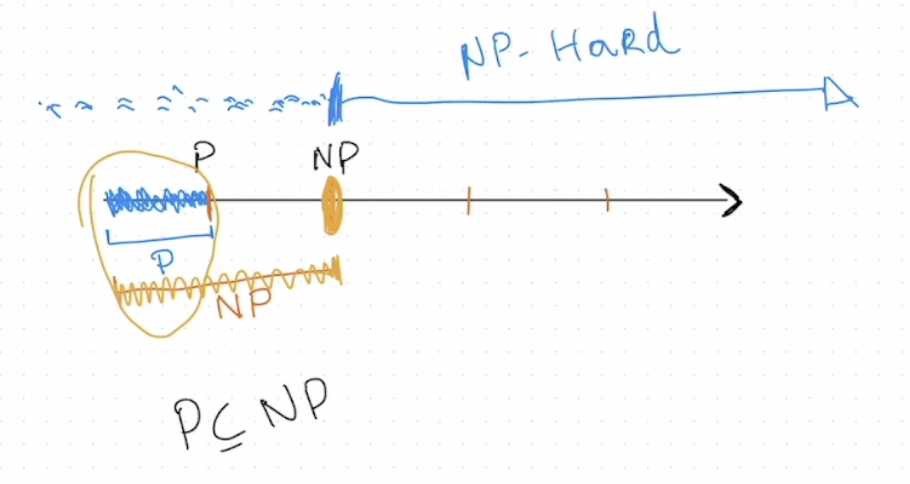
最后我们引入 问题简化 (Problem Reduction) 的定义:

考虑任意的计算问题 $A, B$, 若 所有 $A$ 问题的实例都可通过某个变换 $f_{I_A}$ 映射/转换为问题 $B$ 的某个实例, 则称 $A$ 可被简化为 $B$.

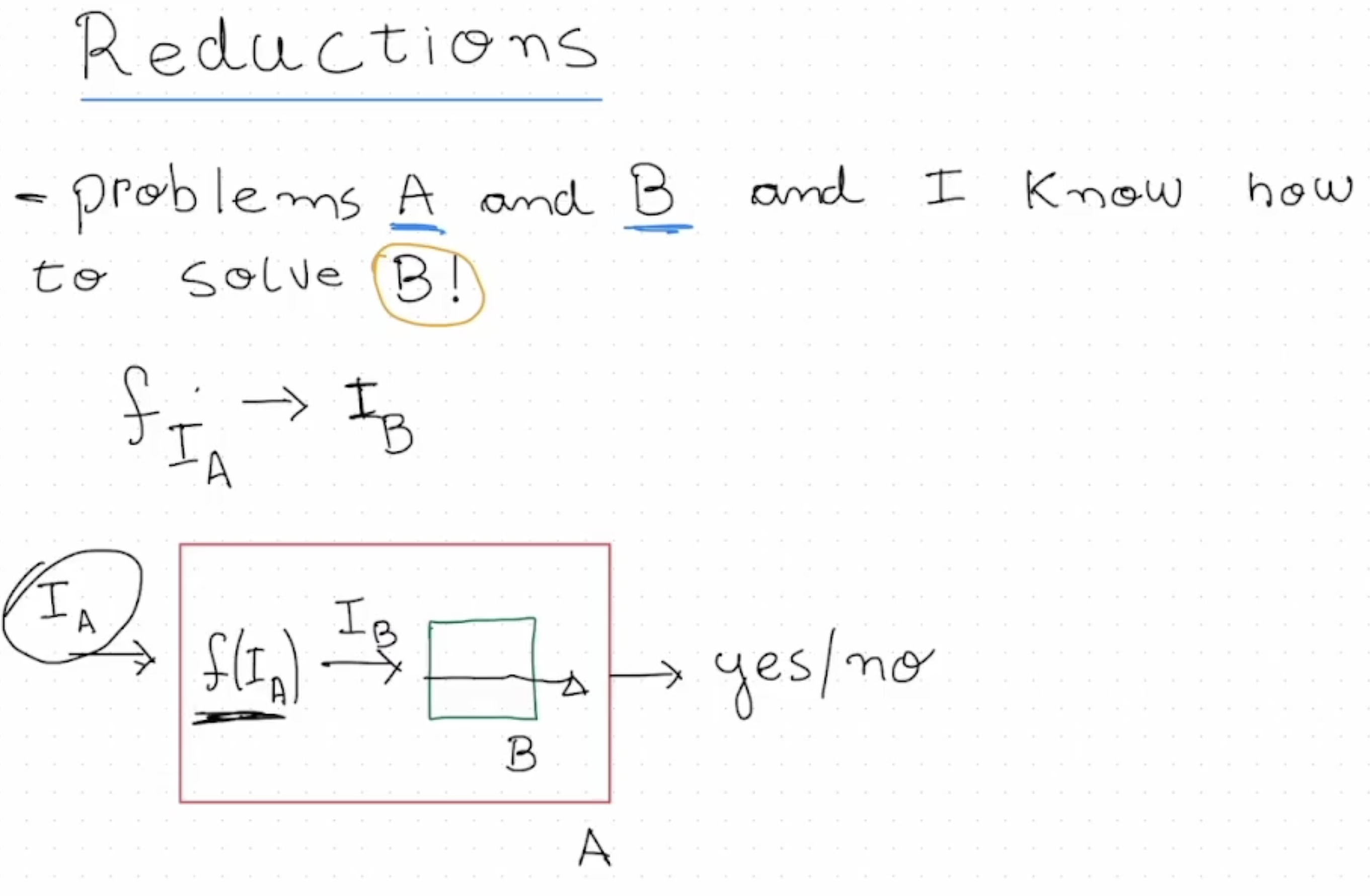
Class P 问题的形式化定义和对问题的编码

我们首先说明如何对问题进行 统一的二进制编码表示 (Encoding). 然后在此基础上给出对 Class P 类问题的 形式化定义.

在研究问题的可计算性时, 我们 只关心决策问题 而非优化问题, 至少不是 直接关注优化问题, 而是关注它的决策问题形式.

广义上说, 决策问题就是一个函数, 它接收一些输入, 返回一个 是或否 ($0$ 或 $1$) 的结果.

并且, 我们可以从一个著名的优化问题: 旅行商问题的例子观察到:

1. 一般来说优化问题都可以 等价地简化为 某个决策问题.
2. 解决决策问题一般不会比解决优化问题更难.

因此, 在考虑优化问题的困难程度和可计算性时, 我们实际考察的是 它的决策问题形式 的困难程度与可计算性.

问题的统一编码

下面, 为了 横向比较 所有 形式, 输入, 输出都不同 的决策问题, 我们需要首先 将它们转化为相同的形式, 这是通过 对问题的编码 (Encoding) 实现的:

我们 假设存在某种通用方法, 可以将 不同的数据结构统一地在多项式时间内编码为二进制序列, 由此对于所有的决策问题, 它们的输入形式现在就是相同的.

因此, 另一种形式上对于决策问题的不同定义是:

所有以一系列二进制数串作为输入, 输出 $1$ 或 $0$ 的函数.

而在经过转换前, 表示问题真实语义 (如下面图中对问题 PATH 的描述) 的描述被称为问题的 语言 (Language), 它表示被形式化后的问题的真实含义.

需要注意的是, 对数字 $n$ 的二进制编码长度仅为 $k = \log_{2}(n)$. 因此, 我们需要注意, 某些问题的时间复杂度可能 关于输入的值的增长为线性的, 但 关于输入长度的增长则为指数级的 .

我们称满足这种特性的问题为 伪多项式时间的问题 (Pseudo-Polynomial), 比如 最简单的素数检测算法. (回顾上一章介绍的内容)

Class P 问题的形式化定义

在介绍了对决策问题的统一化编码方法后, 我们下面给出对 Class P 问题的形式化定义.

首先给出 “可被确定” 的定义:

1. 记算法 $A$ 接纳 某个二进制串 $x$, 当且仅当满足 $A(x) = 1$.

2. 然后, 对任何 被问题的语言 $L$ 描述的二进制串 $x$, 若所有这样的 $x$ 都被 $A$ 接纳, 也就是

   \[A(x)=1 ~~ \text{for} ~ \forall x \in L\]

   且

   \[A(x)=0 ~~ \text{for} ~ \forall x \notin L\]

   则称 问题的语言 $L$ 被算法 $A$ 所确定.

然后给出 “问题的语言 $L$ 能够在多项式时间内被确定” 的 形式化 定义:

如果存在某个 常数 $k$, 对问题的语言 $L$ 中所描述的 任何 二进制串 $x$, 算法 $A$ 确定 $x$ 所需要消耗时间的复杂度为 $O(n^k)$, 则称 该问题的语言 $L$ 能够被算法 $A$ 在多项式时间内确定.

最后, Class P 就是 全体能够被某个算法在多项式时间内确定的问题语言 $L$ 的集合.

Class NP 问题的形式化定义与 Certificate 的定义

下面对 Class NP 给出形式化定义, 并介绍能够表明问题是否位于 Class NP 中的标志: Certificate 的定义.

首先从一个简单的 NP 问题: 图的顶点包含问题 (Vertex Cover Problem) 开始.

图的顶点包含问题 要求检测我们能否找到一个不大于 $k$ 的, 而且 包含了图中所有在任何一条边内顶点 的集合 $C$.

显然, 给定这样的一个集合 $C$, 我们可通过遍历图的边集中每一条边的方式判断, 对于每一条边而言, 是否至少一个顶点位于 $C$ 中. 因此, 判断一个候选答案是否为问题的解 的时间复杂度是 $O(kn)$.

但要从零开始 生成满足条件的一个解 $C$, 在最坏情况下我们需要检查图的顶点集 $V$ 的每一个子集, 因此要检查 $2^n$ 次.

显然这是一个典型的 NP 问题: 无法使用确定性算法在多项式时间内求解, 但是可以在多项式时间内验证候选答案是否为解.

此处对这个问题而言, $C$ 就是它的一个 Certificate, 可被 简单轻松地用来检测问题是否有解. 任何被归类为 Class NP 的问题都有相应的 Certificate, 也正因如此可以看到, $P \in NP$.

用人话说: 任何决策问题都可写为: “给定条件xxx或取值约束yyy, 求是否存在zzz, 使得…条件满足”. 在其中, 所谓的 “问题输入 $x$” 就是给定的条件xxx或问题的取值约束yyy, 如果在问题输入给定的基础下…条件确实满足, 那肯定可以找到对应的一个zzz, 这个zzz就是所谓的, 和问题输入对应的 Certificate.

我们再来考虑更复杂的问题: k-SAT 问题.

k-SAT 问题关注的是 对每个子句中最多有 $k$ 个文字 的合取范式 (CNF) 的可满足性问题. (回顾 COMP21111)

其中, 实际上:

1. SAT 和 3-SAT 问题可互相转换, 并且它们都是 NP 问题, 而且其实它们也都是 NP-Complete 的.
2. 2-SAT 可在多项式时间内被求解.

以及其他的一些 NP 问题:

对于上述的问题而言, 它们的 Certificate 分别为:

1. 满足条件的集合 $S$.
2. 一系列长不超过 $k$ 的操作序列, 可被证明确实满足条件.
3. 现成的, 不超过 $k$ 的一个序列, 可被证明确实是两个字符串的公共序列.

因此, 我们下面给出 基于可在多项式时间内对问题是否有解进行验证 的 Class NP 的定义:

对于给定问题语言 $L$, 如果存在某个 验证函数 $A$, 该函数接受 输入 (如图相关问题中的给定图, 约束满足问题中的表达式, 旅行商问题中的地图和其他约束条件等) $x$ 和对应的 Certificate $y$ (如图相关问题中的子图或顶点子集, 约束满足问题中的一组对变量的解释, 旅行商问题中对应的一组旅行策略等), 可以在 多项式时间内 证明在 $x$ 的条件下 Certificate 是否满足问题要求, 也就是 ($A(x, y)=1$), 则称这样的问题语言 $L$ 属于 NP 类.

而 Class NP 就是所有满足上述条件的问题语言组成的集合.

同时, 我们对应给出 基于非确定性计算 的 Class NP 的定义:

我们称 Class NP 是所有可以使用 在非确定性计算机上运行的算法 在 多项式时间内 求解的问题组成的集合.

在这里, 非确定性计算机 指具有 可以同时执行所有可能的计算 的, 理论上的计算机.

需要注意: 这两个定义是 等价 的. 经过多项式时间的 非确定性计算, 生成的 Certificate 也是 多项式长度 的.

需要注意的是: 如果我们能够制造出这样的 非确定性计算机, 则 P=NP, 反之则有 P!=NP. 由于这样的计算机尚未建成, 但又无法证明我们确实造不出这样的计算机, 因此 我们尚未明确 P=NP 还是 P != NP. (相关习题里有一个与这个结论相关的, 很nasty的题. 顺带一提, 截止目前量子计算机是最接近这一定义的.)

分析计算困难度时对问题实际困难程度简化的技术 (Reduction)

我们在上一节中已经看到, 不同的问题之间存在一定的联系, 某种问题可以被转化为另外一种问题, 而且我们观察到可以互相转换的问题之间, 它们的计算困难度似乎有一定的关联. 下面我们正式介绍 Reduction 的概念, 介绍如何正确地定义 “某个问题必难于另一个问题”.

首先在此处 不加证明 地给出下列结论:

若存在问题语言 $L_1, L_2$, 且 $L_1$ 可在 多项式时间内 被转化为 $L_2$, 则有: $L_1$ 的计算困难度 不高于 (小于等于) $L_2$.

注意: 此处就有结论:

1. $L_1$ 简单不意味着 $L_2$ 一定简单, 但 $L_1$ 难一定意味着 $L_2$ 至少不会更简单.
2. $L_2$ 难不意味着 $L_1$ 一定难, 但 $L_2$ 简单一定意味着 $L_1$ 至少不会更难.
3. 偏序关系 $\leqslant_{P}$ 是具有 传递性 的.

其次给出 Class NPC 的定义:

注意, 任何为 NPC 的问题语言 $L$ 必须同时满足:

1. $L$ 也是 NP 的.
2. $L$ 同时不比 其他任何 NP 问题简单, 也就是说 “任何其他 NP 问题都可 在多项式时间内 被 reduce 为 L”.

相关习题解析

见笔记 “数据结构与算法： 复习”

大脑升级: 重要 NP-Complete 问题一览

在本节中, 我们将简要遍历数种重要的 NP-Complete 问题. 了解这部分知识的主要目的是大脑升级而非清晰明确地了解每种问题的具体细节, 毕竟基本上每个问题本身都很复杂 (以 $0-1$ 背包问题为例, 光是做 Lab 都要做的死去活来), 讲了你也听不懂.

SAT 问题系列

首先回顾重要的 约束满足问题 (SAT) 家族:

各种约束满足问题的 结构特性 是: 我们有由 $k$ ($k$ 不固定) 个不同变量组成的约束或表达式, 而问题的实质是: 找出对这些变量的一组赋值, 使问题结果为 True.

考虑下图所示 Circuit-SAT 问题, 可见该电路的表示可以通过被转化为 3-SAT 从而解决. 不难看出, 3-SAT 的结构可用于表示多种复杂的约束关系.

图相关问题系列

其次了解三种基础但重要的图相关 NP-Complete 问题:

其中:

1. Vertex Cover Problem: 寻找顶点集 $V$ 的子集 $C$ 使图中每一条边中的至少一个顶点都在这个子集中.
2. Clique Cover Problem: 寻找大小不超过 $k$ 的 连通子图 的顶点集, 其实就是在图中寻找 大小不少于 $\vert V-k\vert$ 的独立集 问题的镜像问题.
3. Graph Coloring Problem: 图染色, 确保任一对相联的顶点染上的颜色不同.

以下面的 分房问题 为例, 它就可以被转化为图染色问题.

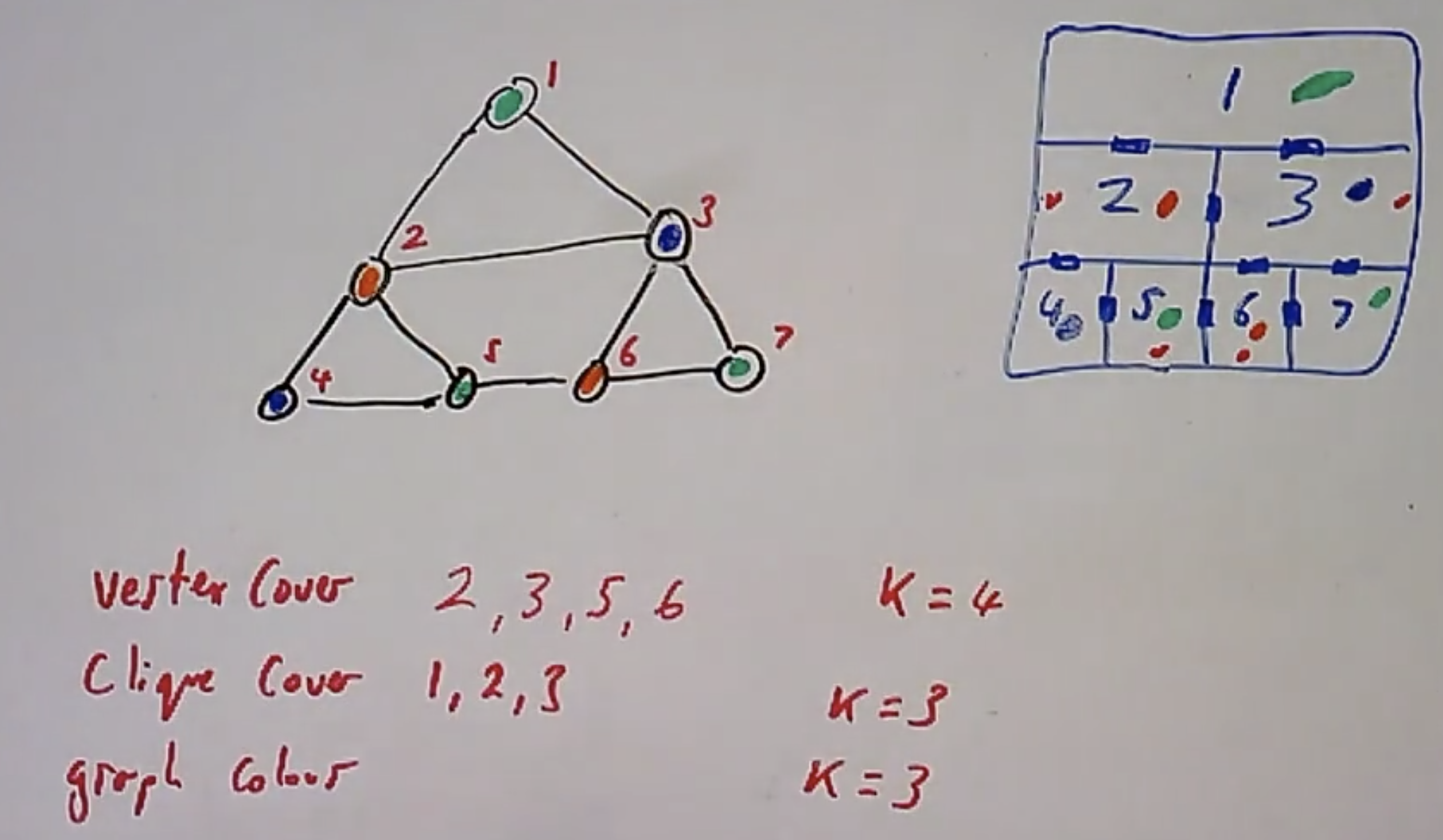
然后是重要的 汉密尔顿环 问题以及 以此作为基础衍生而来 的 旅行商问题:

汉密尔顿环问题要求的是在给定图中 恰好不重复地遍历所有节点 的子环.

而旅行商问题实际上就是有权图中对子环总权重加以限制的汉米尔顿环问题.

举例而言, 考虑下面的两个图, 我们可以在左边的图中找到一个不重复地遍历了图中所有顶点的圈, 而在右侧的图中这样的圈则不存在.

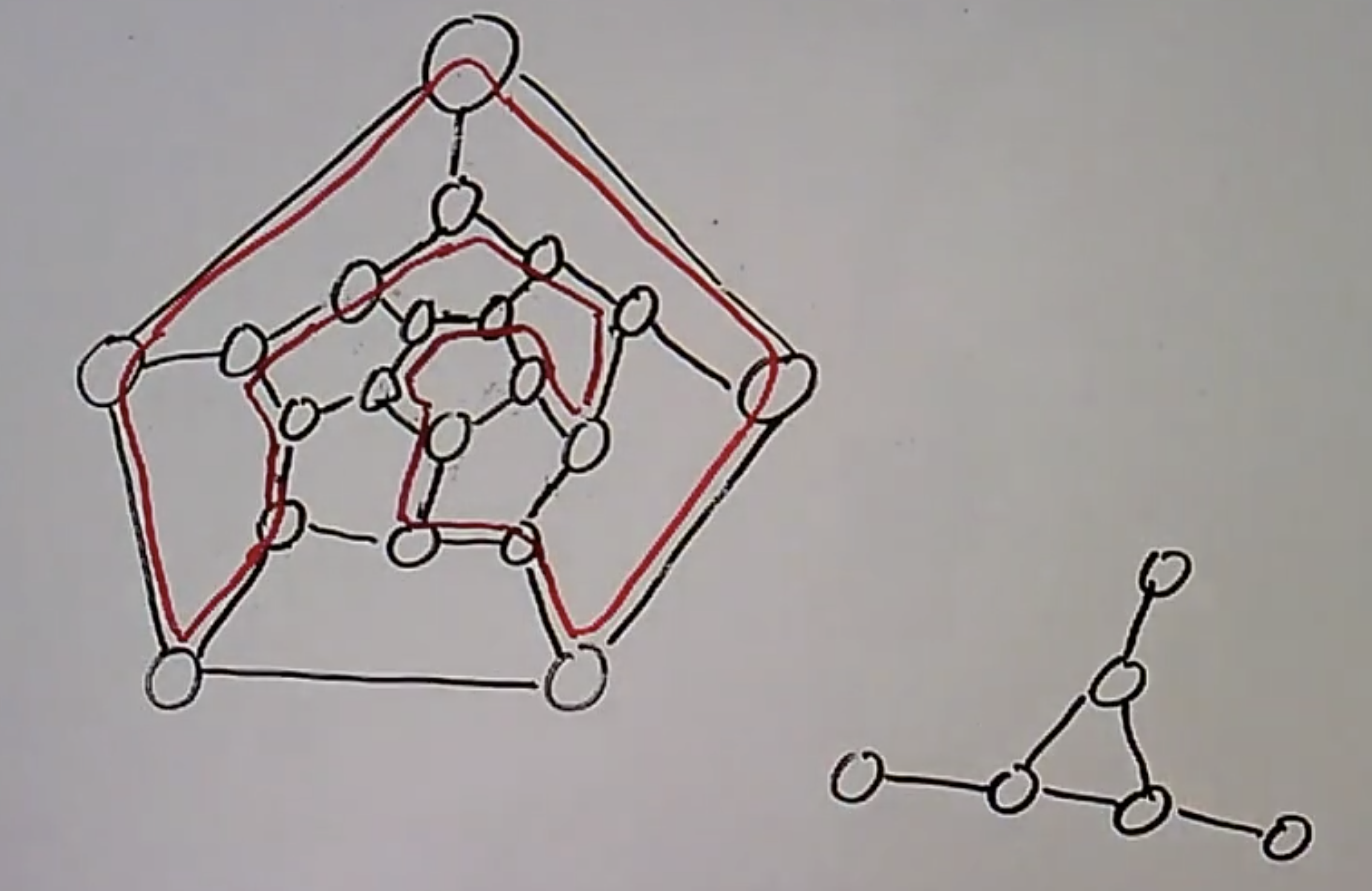
图中最长/最短路径计算问题

首先需要注意: 求图中的最长路径 才是标准的 NP-Complete 问题, 而求图中的最短路径 只是一个 $P$ 问题 (回顾 Dijkstra 算法!)

背包系列问题

然后回顾 背包 系列问题.

首先考虑我们 并不熟悉 的 划分背包问题/打包问题 (Bin Packaging Problem), 其需求是给定一系列体积不同的物体以及对背包容积的约束 B 和分组数量的约束 $k$, 要求能否将给定的这些物体 恰好划分为 $k$ 组, 而且要求 每组中的总占地体积不超过一个背包的最大容积 $B$.

其次回顾我们非常熟悉的 $0-1$ 背包问题. 在此我们无需赘述, 在 Lab5 中我们已经使用了暴力列举, 动态规划和贪心算法实现了对该问题的求解. 而此处需要注意的是: 本 Slides 中提到的 $0-1$ 背包问题 对背包封装方案的最小收益 有限制: 不得低于约束 $V$.

进一步地, 我们再关注对 $0-1$ 背包问题的 等价描述: Subset Sum Problem. 此处不再对定义赘述, 直接看图:

线性规划问题

最后考虑 特殊的线性规划问题:

数章前我们已经介绍了如何使用 单纯形法 求解一般的线性规划问题. 此处需要注意: 整数线性规划问题 是 NP-Complete 的!

整数线性规划问题的定义如下:

而在系数可取值不局限于整数, 而是 实数 时, 就是我们熟知的常规线性规划问题, 可以使用单纯形法求解.

对可满足性问题的简化 (Reduction)

下面我们讨论 Circuit-SAT, SAT 和 k-SAT 之间的 简化问题. 我们将说明:

也就是说, Circuit-SAT 问题可以被简化为 SAT 问题, 而 SAT 问题可被进一步地简化为 3-SAT 问题.

从任何 NP 问题向 Circuit-SAT 的简化

下面我们说明, 任何 NP 问题都可被简化为 Circuit-SAT 问题. 这一性质的推导时通过 Cook Levin 算法实现的:

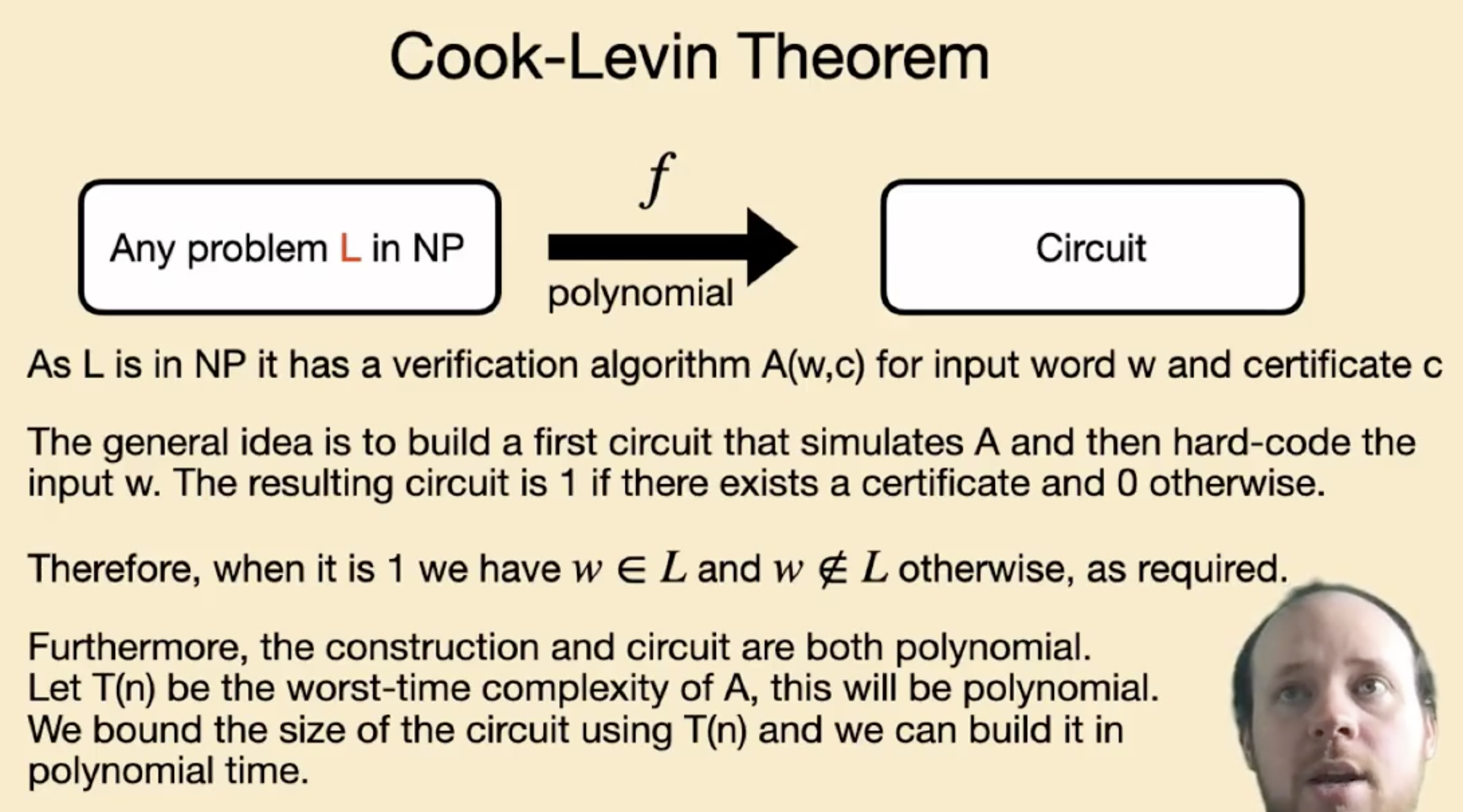
其基本思想是: 任何 NP 问题都一定有一个 验证函数 $V(w,c)$, 其中 $w$ 为问题输入, $c$ 为 (可能存在的) 与输入对应的 Certificate.

而要将该问题转换为 Circuit-SAT 问题, 我们首先需要 模拟原 NP 问题的验证算法 (Verification Algorithm): $A(w, c)$,

然后 将原问题的输入 $w$ 硬编码进验证函数.

若原问题的输入 $w$ 有对应的 Certificate (也就是 $w$ 在原问题的语境下是被接受的), 则电路的输出为 $1$.

若原问题的输入 $w$ 没有对应的 Certificate (也就是 $w$ 在原问题的语境下是被拒绝的), 则电路的输出为 $0$.

进一步地, 还需要证明对电路的构造过程和电路本身都是 多项式的. 这需要同时 限制构造电路耗费的时间 和 限制构造出电路的大小. 这部分只要知道即可, Lecturer 没时间讲明白.

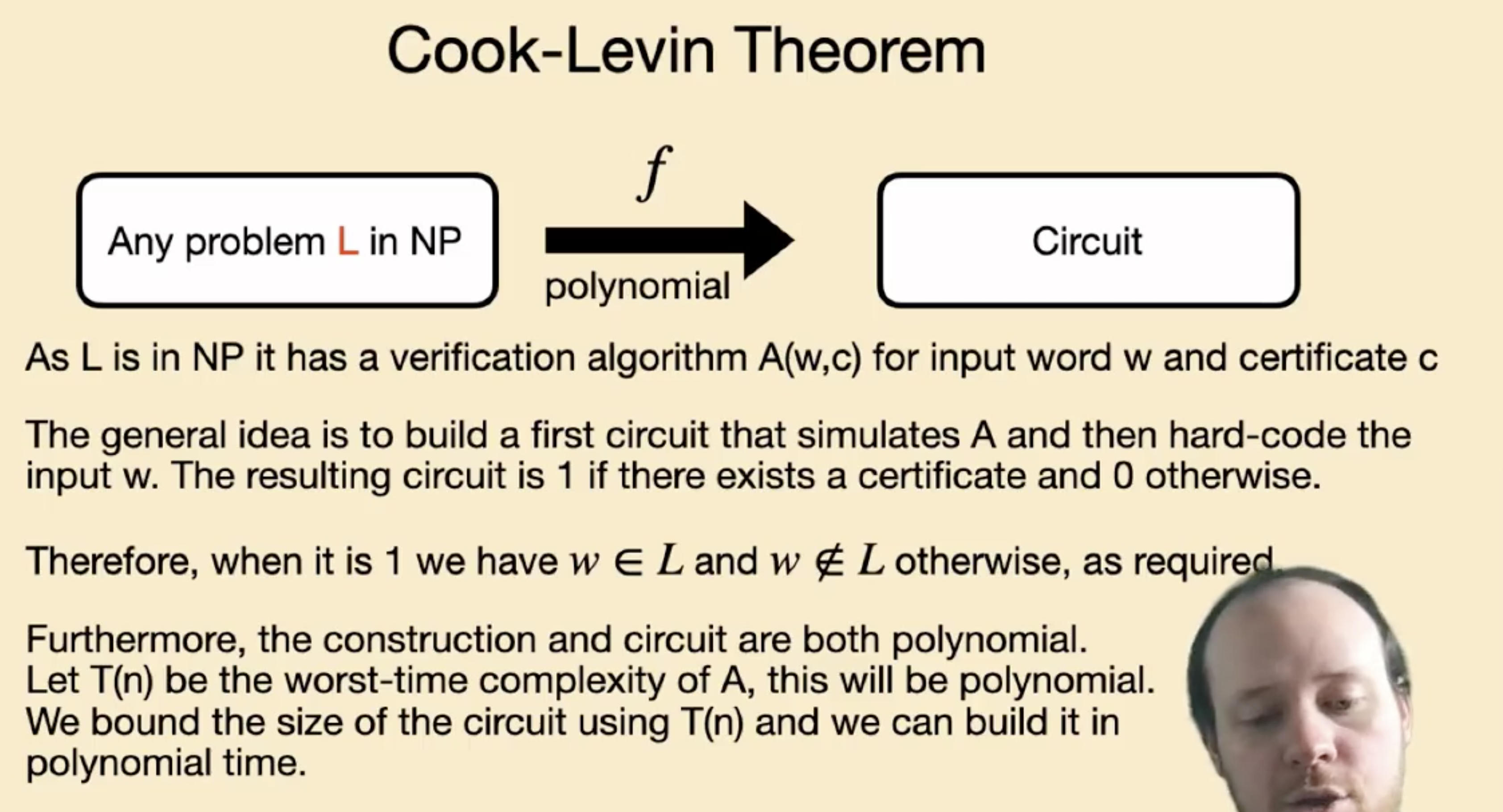
而具体的实现方式是: 使用 Circuit-SAT 中的逻辑门电路 从零开始搭建一个硬编码了验证函数 $V(w, c)$ 的计算机, 它以 $w$ 作为输入, 最终输出为 $0$ 或 $1$.

(丧心病狂, 在iOS 短信应用存储的 gif 图里用逻辑门搭计算机的恶意软件 Pegasus 的开发者直呼内行….)

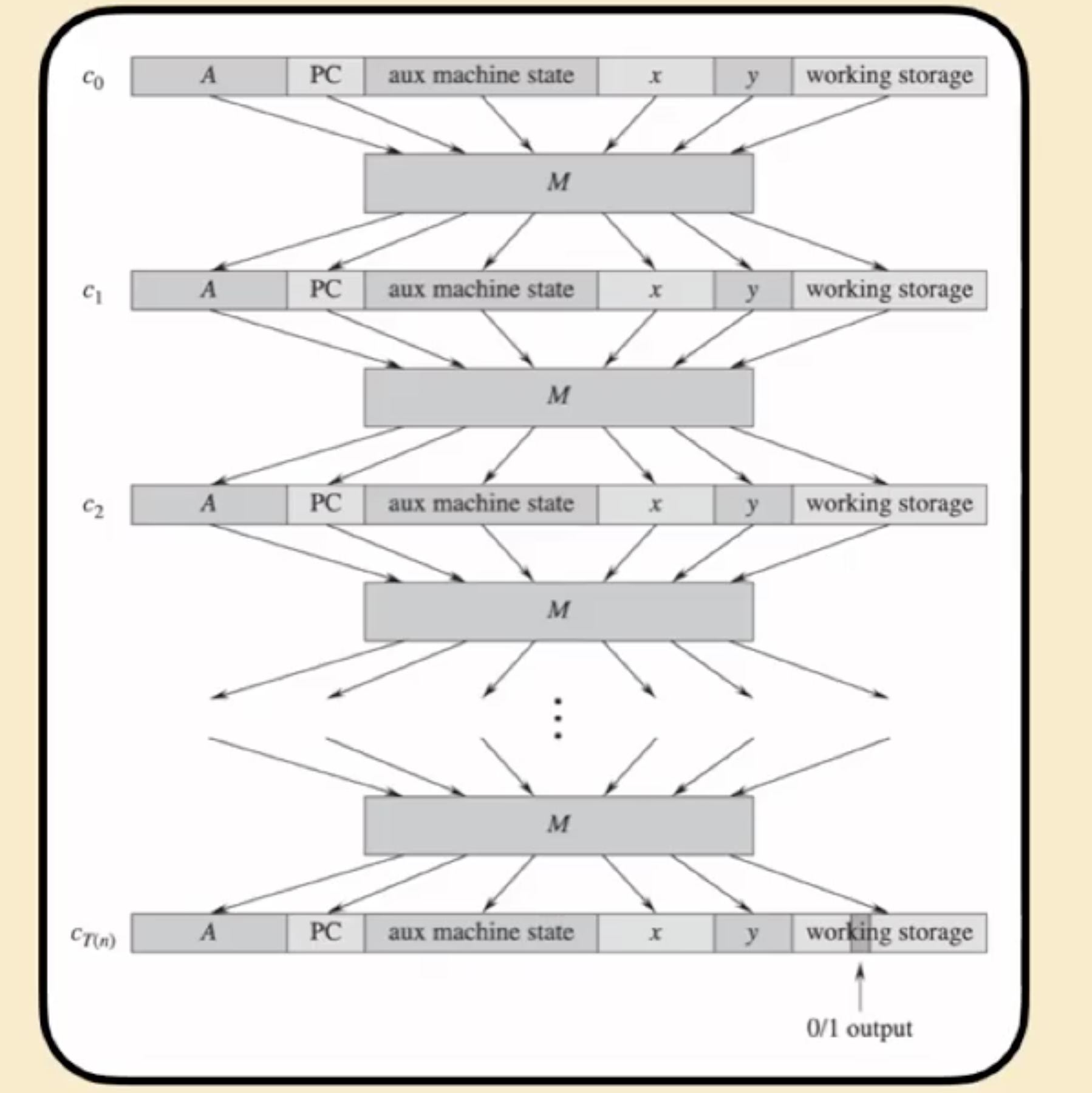
由此, 只要确保搭建计算机所需的运行时间是多项式的, 其状态的数量就是多项式的, 进一步就可说明原问题的输入也是多项式的, 它本质上所表示的问题简化 (Reduction) 也就同样是多项式的.

因此, 使用这一方法我们就可证明:

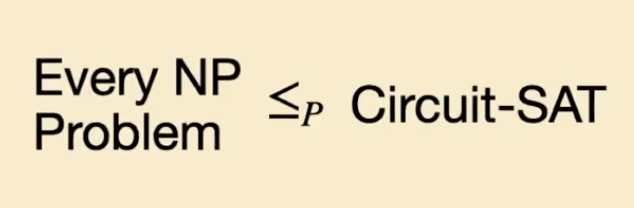
从 Circuit-SAT 向 SAT 的简化

下面再来看从 Circuit-SAT 向 SAT 的简化.

显然, 将电路直接建模为布尔表达式 不是多项式的. 要证明我们期望的结论, 因此我们需要引入新变量 wire, 用下图所示的 Tseytin Transformation 进行多项式的转换:

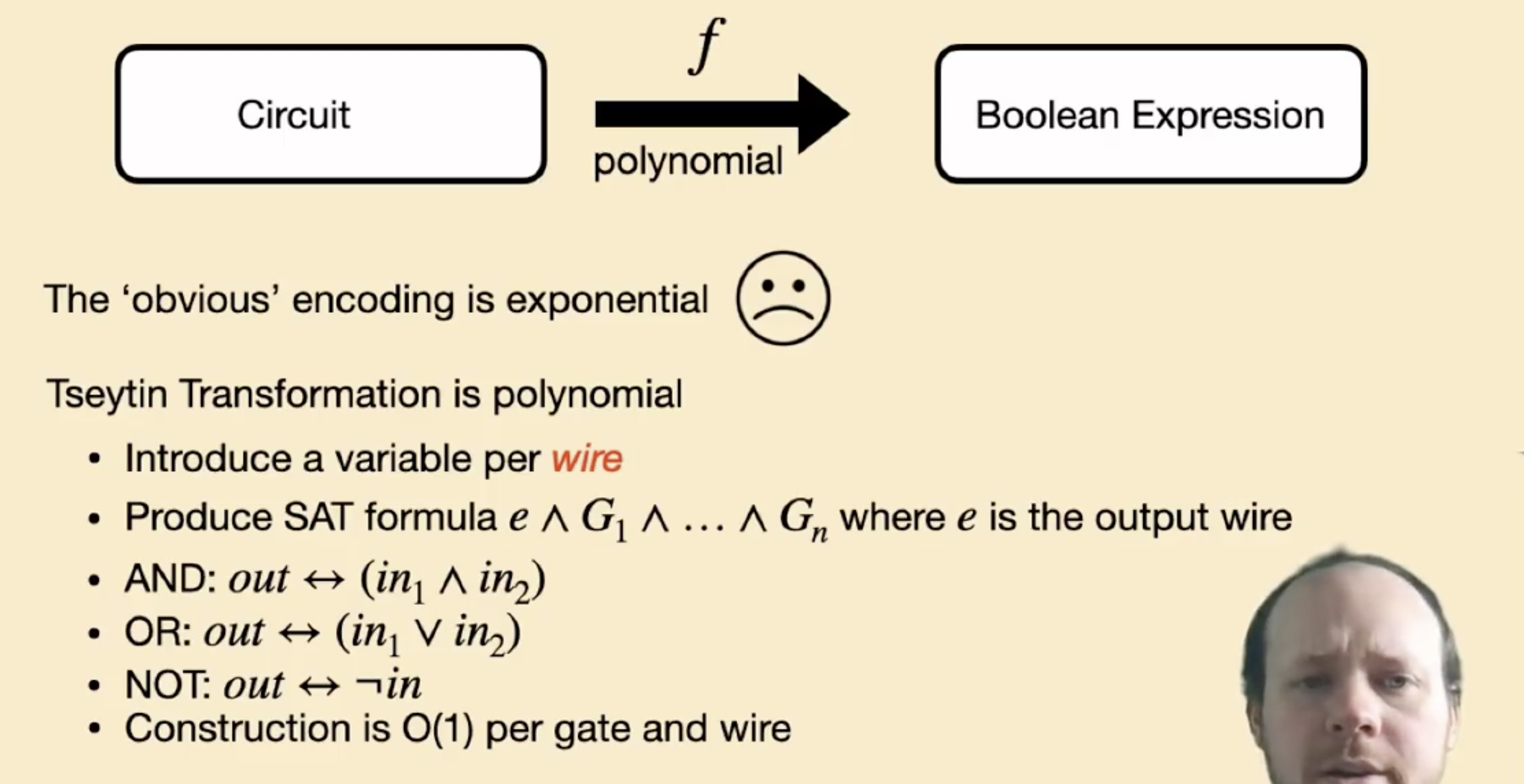
使用 Tseytin Transformation 将一个将 Circuit-SAT 转换为 SAT 的例子如下:

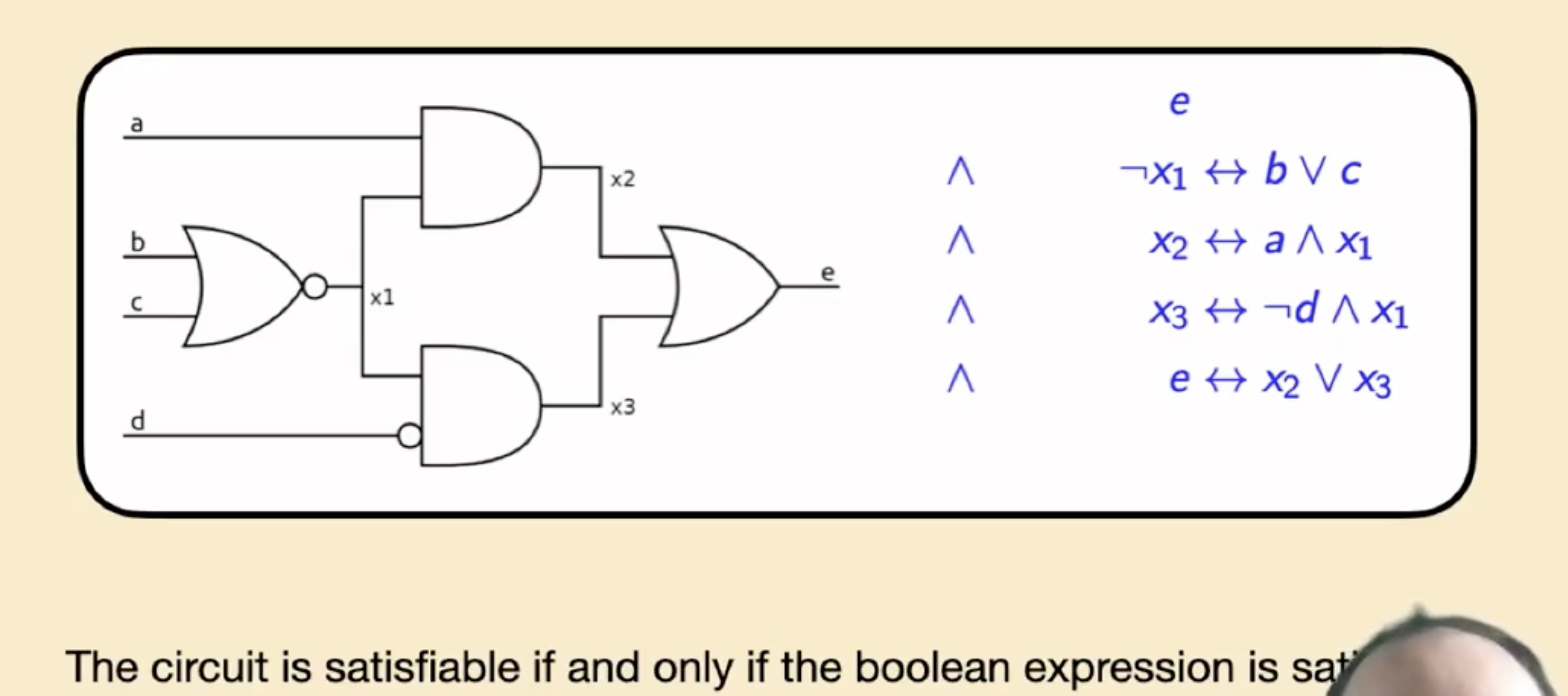
由此我们就可证明结论: $\text{Circuit-SAT} \leq_{p} \text{SAT}$.

从 SAT 向 3-SAT 的简化

同样, 我们需要使用一些奇技淫巧才能实现多项式时间内的转换.

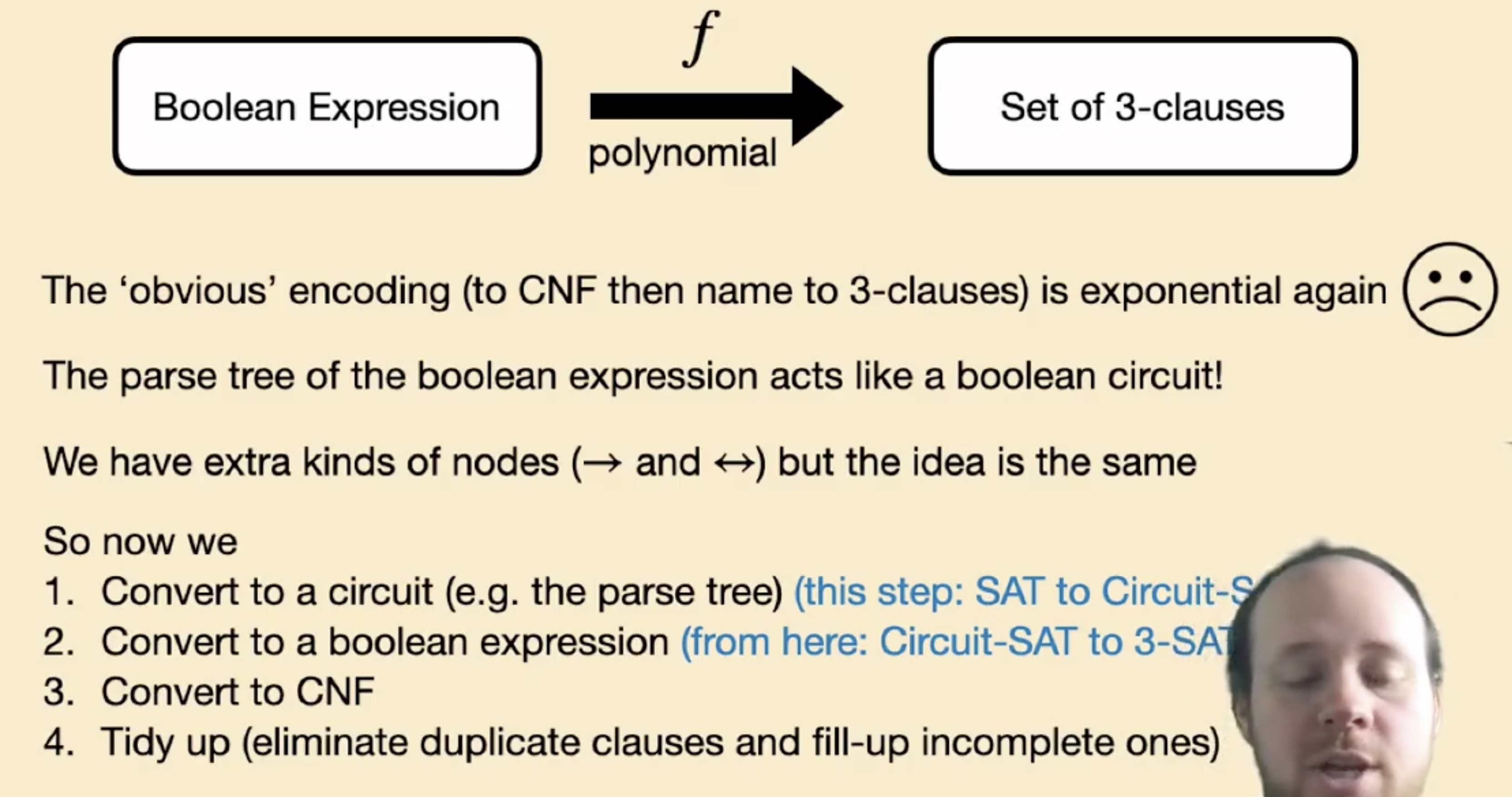
我们需要先将 SAT 转换回 分析树 型的 (抽象) 电路, 然后再从它转换到 $3-SAT$, 如下面的例子所示:

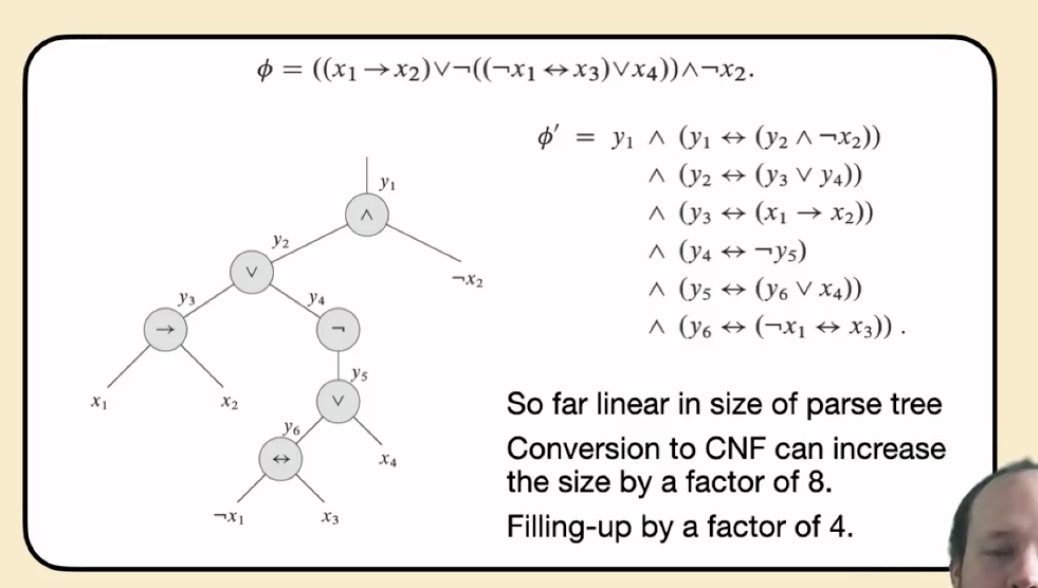
最终我们就可证明所需的结果:

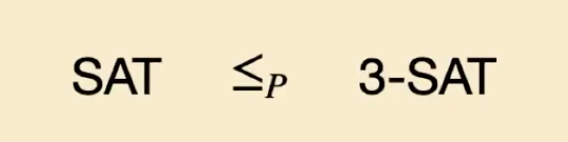
总结如下:

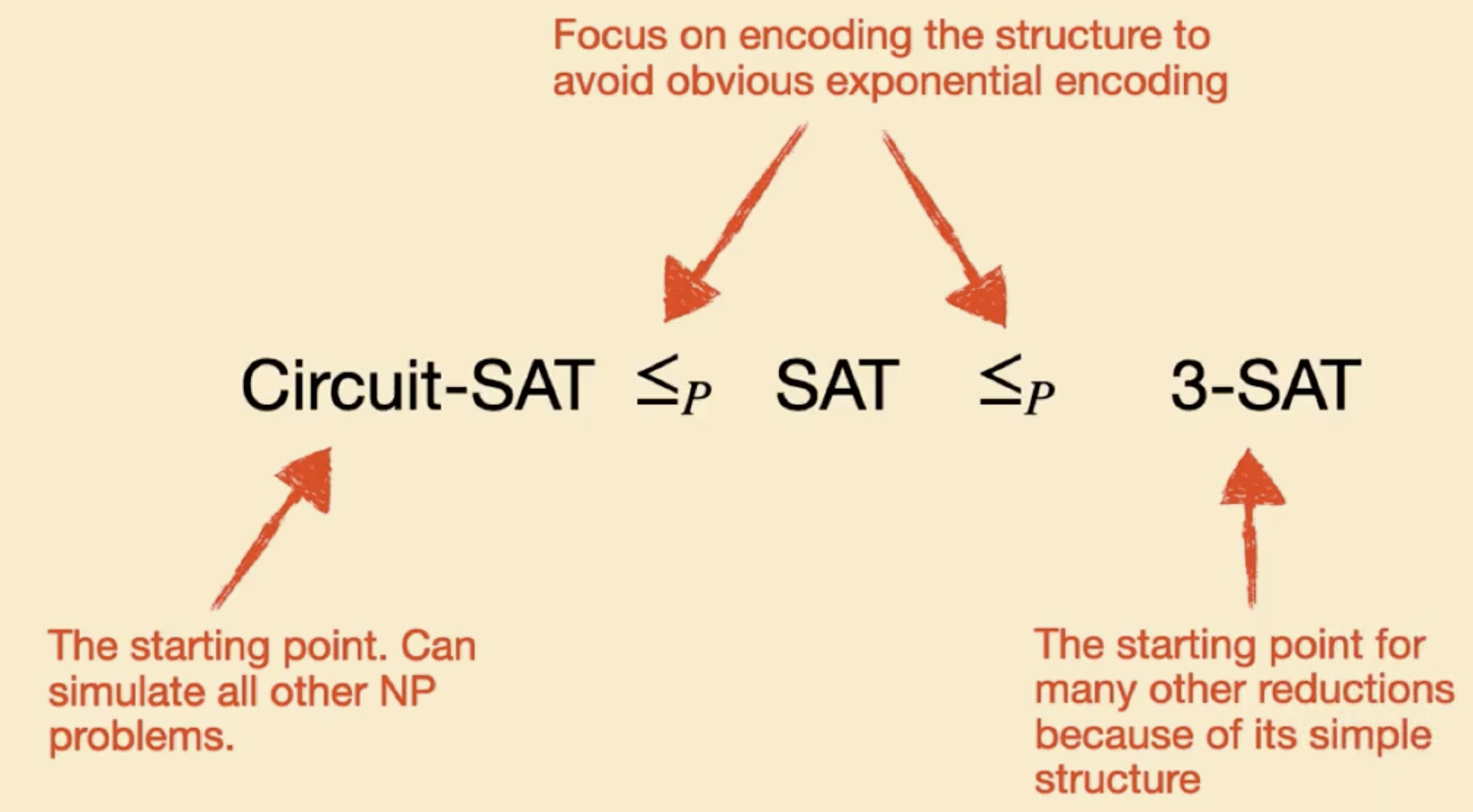
从 3-SAT 向 Clique 的简化

下面我们讨论从 3-SAT 向 Clique 的简化:

Clique 问题实际上就是考察: 给定图 $G$ 和约束 $k$, 问该图中是否存在大小为 $k$ 的连通子图.

而下面我们的目的是: 构造一个映射, 将每个 3-SAT 问题映射为对应的 Clique 问题.

基本思路是: 被构造的图 $G$ 中的节点 将被拆分为 $k$ 个 三元组 (Triples), 而每个三元组都和 原来的 3-SAT 中的一个子句对应. 这样我们就得到了图 $G$ 的顶点集 $V$.

而连接边 (构造图 $G$ 的边集 $E$) 的原则是:

1. 在同一个三元组中的顶点 永不相连.
2. 不连接 符号相同 但 正负性质不同 的顶点, 如形如 $a_1$ 和 $\neg a_1$ 的顶点就不能相互连接, 但 $a_1$ 和 $\neg b_2$ 就可相连.

随后, 我们得到的 Clique 问题就等价于原来的 3-SAT 问题.

举例而言: 使用上述的规则转换图中的 3-SAT, 在图大小约束为 $3$ 的情况下, 显然可以在图中找到一个大小为 $3$ 的连通子图, 将连通子图顶点对应的文字赋值设为 $1$ 就得到了原 3-SAT 的一个翻译.

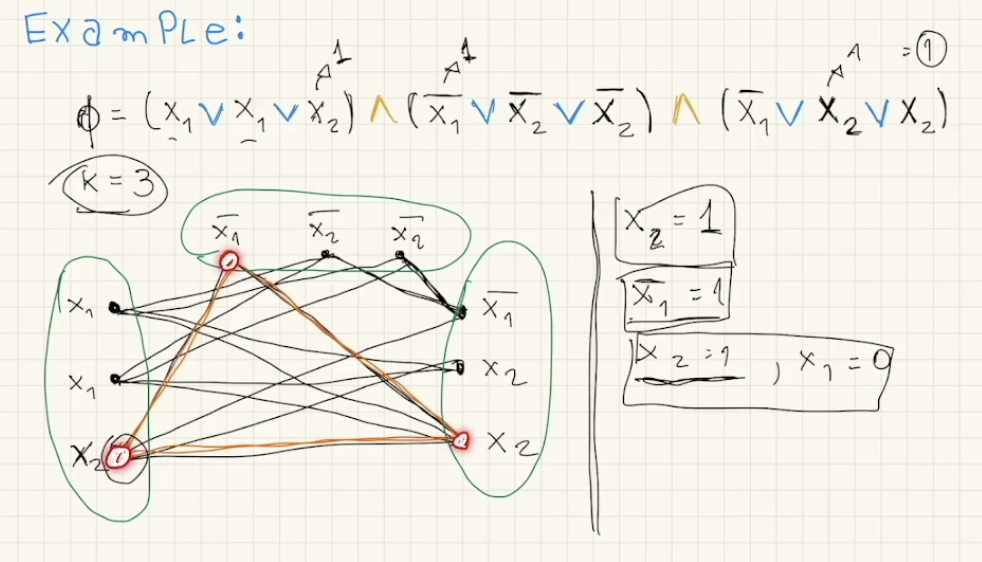
对图相关问题的简化

本节讨论我们艰难旅程的最后一步: 对图相关问题的简化.

我们考虑从 VertexCover 向 Clique 的简化:

此处的简化目的是: 给定输入的图 $G = (V, E)$ 和 Cover 的大小 $k$, 要求输出一个在 Clique 语境下, 大小不超过 $k’$ 的新图 $G’ = (V’, E’)$.

而这个新图满足:

1. $V’ = V$
2. $E’ = \bar{E}$, 也就是对 $E$ 在 全体可能边集 中的 取反.
3. $k’ = \vert V \vert -k$.

此处的原理是: $G$ 只能够存在某个最多大小为 $k$ 的 Cover: $C$ $\leftrightarrow$ $E$ 中的任何一条边上的至少一个节点在 $C$ 里 $\leftrightarrow$ 只要任两个节点 $u, v \notin C$, 则 $(u, v) \notin E$ $\leftrightarrow$ $(u, v) \in \bar{E} \leftrightarrow$ 集合 $V-C$ 就是一个大小最多为 $\vert V \vert -k$ 的团.

进一步考虑从 3-SAT 向 3-Color 的简化:

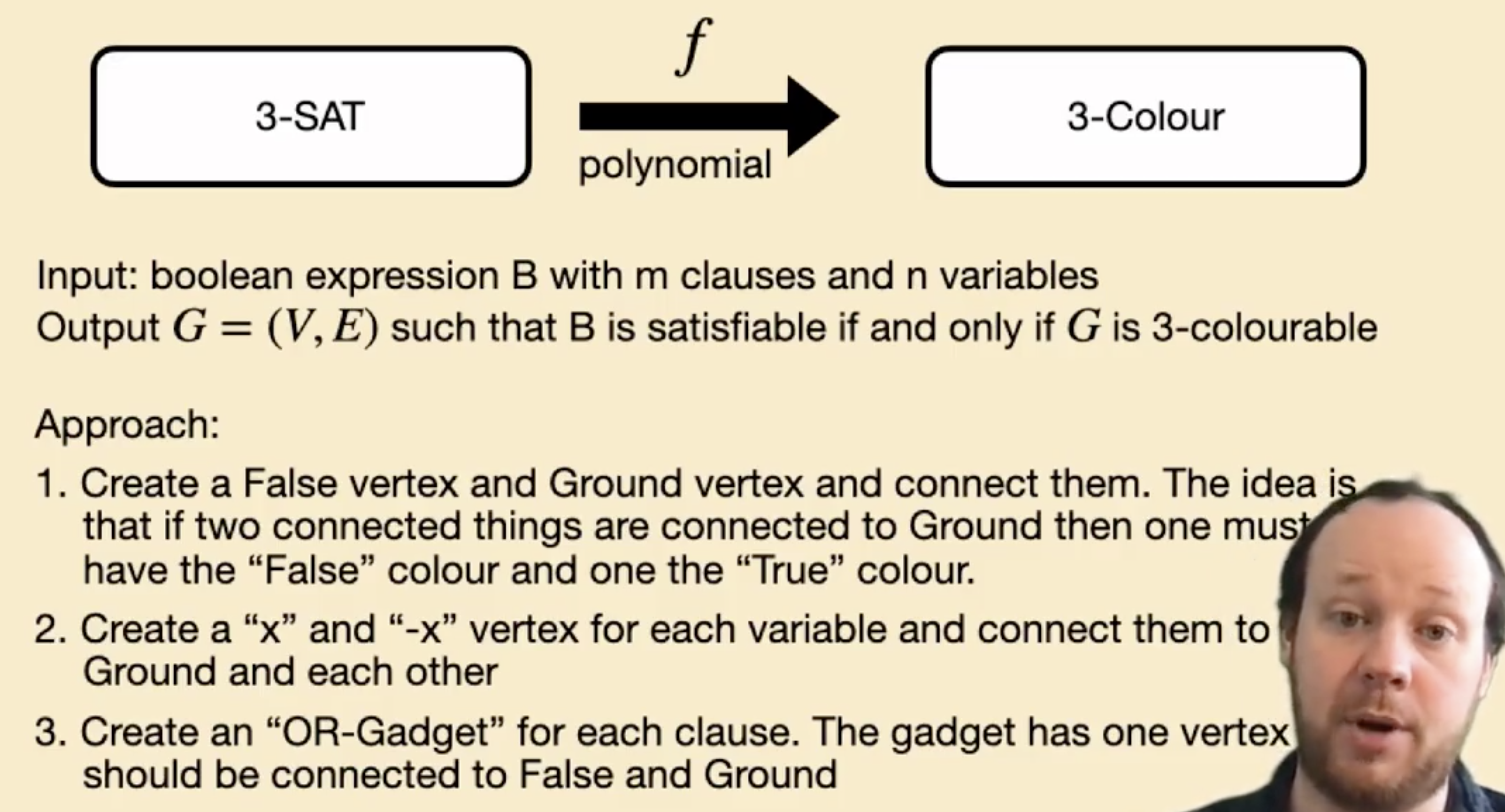
注意此处在构造子句对应的子图时, 我们引入了 Or Gadget.

再进一步地, 可以依次从 3-SAT 简化到 k-SAT:

(这里有时间再补, 没时间就算了, 记结论就行)

最后对我们所介绍的各种 NPC 问题列举总结:

1. Circuit-SAT
2. SAT
3. 3-SAT/k-SAT with k >= 3
4. Vertex Cover: find a subset C of V so that for each edge in E at least one node is in C given the constraint on maximum size of C
5. Clique: inverse question on independent sets, find complete sub graph’s vertex set C with constraint on the maximum size of C.
6. Graph Colorng: assign color to every nodes, but each pair of neighbors cannot share the same color.
7. Hamiltonian Cycle: find a shortest circle in graph that connect every vertex.
8. Bin Packing: separate the set into k subsets where each subset’s total weight is no more than P.
9. 0-1 knapsack: given a list of weighted items and a bag no heavier than P, find an optimal combination of items to pack into the bag so that the weight constraint does not exceed but the total value can be maximised.
10. Integer programming: stricter linear programming, where each variables’ value can only be integer.

相关习题解析

见笔记 “数据结构与算法： 复习”.

• Previous
  数据结构与算法： 素数查找问题
• Next
  数据结构与算法： 复习