素数检测问题
在本章中, 我们考虑 寻找素数 的问题. 由 素数定理 (Prime Number Theorem):
记 $\pi(n)$ 为 数值小于等于 $n$ 的所有数中素数的个数, 则对任意 $n$, 有:
\[\lim_{n \rightarrow \infty} \frac{\pi(n)}{\frac{n}{\ln(n)}} = 1.\]也就是说, $\frac{n}{\ln(n)}$ 给出了 小于等于 $n$ 的素数个数 的 近似.
因此可知, 考虑一个 足够大 的数 $n$, 则在前 $n$ 个数中有
\[\pi(n) \approx \frac{n}{\ln(n)}\]个素数.
因此, 在前 $n$ 个数中 随机抽取一个, 得到的数确实是素数的概率为
\[\frac{\pi(n)}{n} = \frac{1}{\ln(n)}.\]比如, 如果我们需要找到一个二进制位长为 $1024$ 的整数, 则需要检查 $\ln(2^{1024}) \approx 710$ 次.
素数定理告诉我们, 寻找素数问题等价于 检测某个范围内的随机数是否为素数 的问题.
素数检测的基本方法与核心思想
下面讨论检测素数的核心思想与基本方法: 暴力测试 和 费马小定理, 并进一步解释为何 伪素数的存在决定我们无法直接使用费马小定理检测素数.
从定义出发, 素数是只被自身和 $1$ 整除的数. 并且我们知道, 考虑数 $n$, 由于检查大于 $\sqrt{n}$ 且小于 $n$ 的数是否整除 $n$ 实际上就是在检查位于 $1$ 到 $\sqrt{n}$ 之间的数能否整除 $n$, 因此有:
暴力测试
最基本的 暴力测试 (Trial Division) 就是在 $1$ 到 $\sqrt{n}$ 之间的数字中挨个检查它们能否整除 $n$ (当然, 除了 $1$ 以外). 如果它们中只要有一个能整除 (当然, $1$ 例外), 就说明被测数 $n$ 不为素数:

费马小定理和伪素数 (Carmichael Number)
进一步地, 我们还知道 费马小定理 的结论:
对任意整数 $x$ 和素数 $p$, 若 $x ~\text{mod}~p \neq 0$, 则均满足
\[x^{p-1} ~\equiv~ 1 ~ (\text{mod} ~ p)\]因此看上去, 利用时间复杂度为 线性 的 快速模幂算法 随机挑选满足条件的整数 $x$, 测试 $x^{n-1}$ 即可检测被测数 $n$ 是否为素数.

然而不幸的是, 满足费马小定理只是一个数 $n$ 为素数的 必要条件, 一类被称为 Carmichael Numbers (伪素数) 的合数 (非素数) 同样满足费马小定理:

因此, 由于伪素数的存在, 我们无法直接应用费马小定理检测某个数 $n$ 是否为素数.
随机素数判定法
下面介绍 随机素数判定法 (Randomized Primality Testing):
基于上面一小节的描述, 我们知道满足费马小定理的数 可能是素数, 额可能是 Carmichael 伪素数. 由于在现实中 小概率事件几乎不可能发生, 因此只要我们找到一种 出错概率可控 的素数判断函数, 将 它的出错概率控制在足够小的水平上, 那么我们就可以放心地将它应用到实践中.
考虑一个这样的函数, 记为 $\text{witness}(x, n)$, 用于 判定一个数是否为合数:
- 若 $n$ 为素数则该函数返回
false - 若 $n$ 不为素数, 则该函数有 $q < 1$ 的概率也返回
false
称其为 见证函数:

下面结合见证函数 \text{witness}() 介绍 随机素数判定法 (Randomized Primality Testing Algorithm):

其中, $n$ 为 需要被检测的数, $k$ 称为置信度, 表明我们希望以多高的确定率 (准确率) 进行素数判定.
注意此处 $t$ 为执行随机测试的次数, 每一次测试中我们都会生成一个随机数 $x$ 作为见证函数的另一个输入.
如果在所有的随机测试中 $\text{witness}(x)$ 均判定数 $n$ 为素数, 则 在置信度为 $k$ 的前提下, 可判定 $n$ 为一个素数.
下面说明 $t$ 如此取值的原因.
首先进一步解释 置信度 $k$, 它实际上约束的是 判定函数出错的概率. 判定函数出错的概率需要为
\[2^{-k}.\]而函数整体返回 false 的概率客观上是 $q^{t}$, 因为在这一情况下任何一次检测中见证函数都需要返回 false.
因此目标是
\[q^{t} \leqslant 2^{-k}\]因此有
\[t \leqslant \log_{q}(2^{-k}) = \frac{k}{-\log_{2}(q)} = \frac{k}{\log_{2}(\frac{1}{q})}.\]由此计算出 $t$ 的上界. 因此我们有:
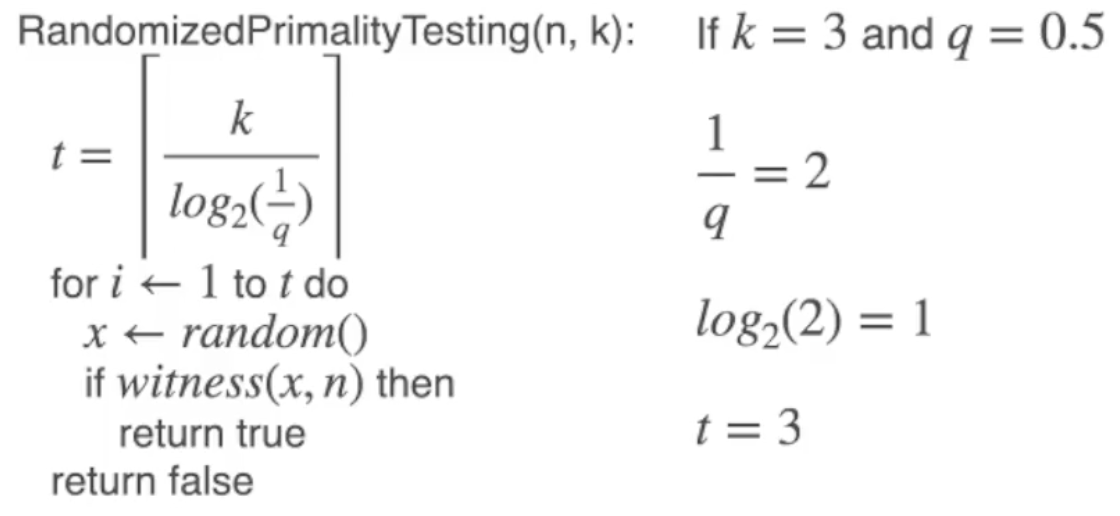
Rabin-Miller 素数判定法
最后介绍 Rabin-Miller 素数判定法:
Rabin-Miller 素数判定法 实际上就是一种特殊的随机素数判定法. 我们首先介绍它的见证函数.
回顾定义可知, 见证函数 $\text{witness}(x, n)$ 是 接受随机输入 $x$, 检测某个数 $n$ 是否为素数 的函数, 若 $n$ 为素数的话返回 false, 否则以 $1-q$ 的概率返回 true.
因此, 基本思路是基于 费马小定理, 检查 $x^{n-1} ~\text{mod}~(n) ~\equiv~ 1$ 是否成立, 并痛苦地接受费马小定理误报 Carmichael Number 伪素数为素数的特殊情况.
我們同時有以下結論 (二次探測定理):
若 $p$ 为素数 $x$ 為 任意整數, 則如果有
\[x^2 ~\text{mod}~p~\equiv 1\]则
\[x ~\equiv~ 1 ~ \text{mod} ~p\]或
\[x ~\equiv~ -1 ~ \text{mod} ~p\]若 $0 < x < p$, 则解必為 $x=1$ 或 $x = p-1$.
进一步地, 基于数分解知识可知:
若 $n$ 为 奇数, 则 $n-1$ 可表示为:
\[n-1 = 2^k \cdot m\]其中 $m$ 为某个不可再被 $2$ 分解的奇数.
由于即是偶数又是素数的只有 $2$, 因此在绝大多数情况下我见证函数的检查对象只会是奇数. 故在利用费马小定理进行素数检测时, 可以将
\[x^{n-1} ~\text{mod}~ n\]表示为
\[x^{2^k \cdot m} ~\text{mod}~ n\]其中 $2^k \cdot m = n-1$, 然后我们可以依次检测数列
\[x^{2^k \cdot m}, x^{2^{k-1} \cdot m}, \cdots, x^{m}.\]若:
-
若 $n$ 可能为素数, 则對上述的序列中的 $x^{2i \cdot m}, i=k, k-1, …, m$ 取關於 $n$ 的餘數, 第一個必然為 $1$, 而剩下的序列中 第一個不為 $1$ 的數必然是 $-1$.

-
若 $n$ 为合数, 则从 $x^{m}$ 反推, 自 $k=0$ 开始到某个 $k=t$ 为止模运算结果都不为 $\pm 1$, 而 $k > t$ 时模运算结果均为 $1$ 或都不为 $1$.
(換言之, 對於 $n$ 為合數的情形, 從序列開頭 $x^{2k \cdot m}$ 開始取於數, 要麼 一個 $1$ 都沒有, 要麼是一串 $1$ 後面緊跟著第一個數不為 $-1$.)

也就是:

这样就完成了一种见证函数, 也就是 Rabin-Miller 算法 的实现.
下面讨论该见证函数的错误率:

也就是說, Rabin-Miller 算法的錯誤率最多為 $\frac{1}{4}$. 因此對於給定的顯著水平 $k$, 若將 Rabin-Miller 函數作為隨機素數判定法的 見證函數, 則知循環次數 $t$ 為:
最后给出 Rabin-Miller 算法的 时间复杂度:

該算法的時間複雜度是 $O(k \cdot \log(n)).$
相关习题解析
见笔记 “数据结构与算法: 复习”.
