El Gamal 加密算法
本节简单介绍 El Gamal 加密算法的基本原则, 涉及的计算算法和操作步骤.
El Gamal 加密算法的基本原则
El Gamal 算法是一种 公钥-私钥 加密算法, 其基本思路是: 构造一个 从自变量计算出因变量相对容易, 但反过来给定因变量反推自变量极其困难 的 单向函数.
而在公钥-私钥加密算法中, 我们将包含部分自变量信息, 可以用于解密的信息作为 私钥, 只有信息接收者拥有; 而信息接收者通过使用私钥生成 可以加密信息但无法将密文解密 的 公钥 自由分发, 任何人都可以使用公钥向接受者发送加密的信息, 而这些信息 只有掌握私钥的接受者自己 才能解密.

在 El Gamal 算法中, 核心的加密思想涉及下列的单向函数:
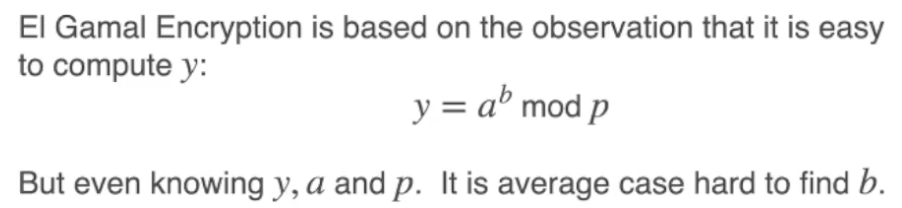
在知道 $y, a, p$ 的情况下反推出 $b$ 基本是不可能的.
下面介绍一些在 El Gamal 算法中涉及的数论概念:
模运算

下面给出 剩余系, 简化剩余系, 模逆 (Modular Inverse), 生成元 (Generator) 和 原根 (Primitive Root) 的定义:
剩余系, 简化剩余系和模逆
记 $\mathbf{Z}_n$: 模 $n$ 的剩余系.
同时有结论: 若 $x$ 和 $n$ 互素, 则 $x$ 在 $\mathbf{Z}_n$ 中的代表元对于 $n$ 有 模逆, 即:
存在 $x$ 在 $\mathbf{Z}_n$ 中的模逆 $x^{-1}$, 使得
\[x \cdot x^{-1} \equiv 1 ~ (\text{mod} n).\]记 $\mathbf{Z}^{*}_n$: 模 $n$ 的 简化剩余系: 其中任何代表元 均和 $n$ 互素.
故对素数 $p$, 有: $\mathbf{Z}_p = \mathbf{Z}^{*}_p$. 立即可知:
-
素数的剩余系就是其简化剩余系.
-
素数的剩余系中的任何代表元都关于该素数的模运算存在模逆.
阶, 生成元和原根
记 $m$ 为素数 $p$ 的简化剩余系中的一个代表元. 若存在 $k$, 满足
\[m^1 ~ \text{mod}~ p, m^2 ~ \text{mod}~ p, \cdots, m^{k} ~ \text{mod}~ p\]恰好构成了 模 $p$ 的简化剩余系, 则称 $k$ 为数 $m$ 在 $p$ 的简化剩余系中的 阶, 方便记忆可记为 “$m$ 关于 $p$ 的阶”, 你自己知道实际上表示什么含义就行.
若 $m$ 关于 $p$ 的阶恰为 $p-1$ (任何素数 $p$ 的剩余系, 简化剩余系恰含 $p-1$ 个代表元), 则称 $m$ 为 $p$ 的简化剩余系的 一个 生成元 (Generator), 或称 $m$ 为 $p$ 的一个 原根 (Primitive Root).
下面给出一些关于生成元存在性的证明:

可以不记, 官宣不考.
El Gamal 加密算法中涉及的计算算法
下面介绍一些 El Gamal 加密算法中涉及的必须计算算法. 由于大概率这些算法 要求记忆, 请务必 谨慎对待.
欧几里得算法
欧几里得算法用来计算 两个数的最大公约数:
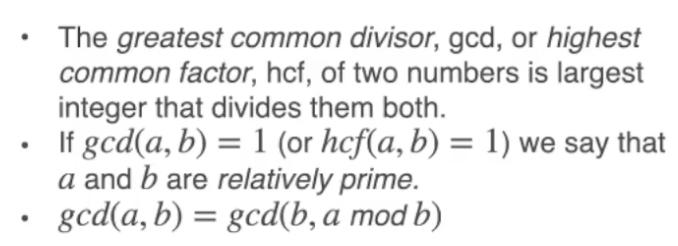
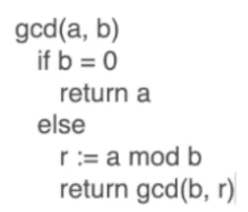
快速欧几里得算法
快速欧几里得算法用来计算 模逆, 应用在 解密过程中. (计算的是 $a^{-1} ~\text{mod}~b$, 就是返回的 $j$)


快速模幂算法
快速模幂算法用于给定 $p, q, x$, 计算 $q^x ~\text{mod}~ p$, 应用在 加密过程中. (按照下图算法计算的是 $a^{p} ~\text{mod}~ n$)

El Gamal 加密算法的操作步骤
创建公钥和私钥
El Gamal 算法的 公钥:

注意:
-
$g$ 是 $p$ 的 原根, 考试时会直接提供.
-
$x$ 是 $p$ 的简化剩余系中的任意元素, 除此以外没有选择限制.
El Gamal 算法的 私钥:
构造公钥时, 在 $p$ 的简化剩余系中挑选的 $x$ 就是 只有信息接收者持有的 私钥.
加密
El Gamal 算法中的加密过程是:
-
信息发送者接收到广播的私钥: $(p, g, y)$.
-
信息发送者选择要发送的信息 $M$.
-
信息发送者 随便选择某个数 $k$.
-
信息发送者发送密文:
\[(g^k ~\text{mod}~p, ~M\cdot y^k ~\text{mod}~p).\]
解密
记信息接收者得到的信息为
\[(a, b).\]解密步骤:
- 使用私钥 $x$ 计算 $a^{x} ~\text{mod}~p.$
- 计算 $a^{x} ~\text{mod}~p.$ 关于 $p$ 的 模逆 $r$.
- 计算 $b \cdot r ~\text{mod}~p$, 所得结果即为明文.
回顾构造密文的精密之处: 站在旁观者角度我们知道这里的 $y$ 实际上就是 $g^{x} ~\text{mod}~p$. 在解密时, 解密者只需用私钥计算出 $g^{kx} ~\text{mod}~p$, 进一步算出这个数关于 $p$ 的模逆, 乘上 $M\cdot y^k ~\text{mod}~p$ 就恢复得到了被加密的明文.
