渲染
在前面依次讨论完图形管线的基本组成, 顶点和边的渲染与近似, 几何变换的表示, 曲面的表示/存储和上色, 视角的确定和投影后, 我们在本章中讨论对物体表面的渲染问题.
此时, 我们所得到的是在屏幕平面上已经处于合适的视角, 清除了隐藏面的网格. 要进行渲染, 就需要结合 光照模型 (Illumination Model) 的基础上对网格表示的曲面进行 平滑上色.
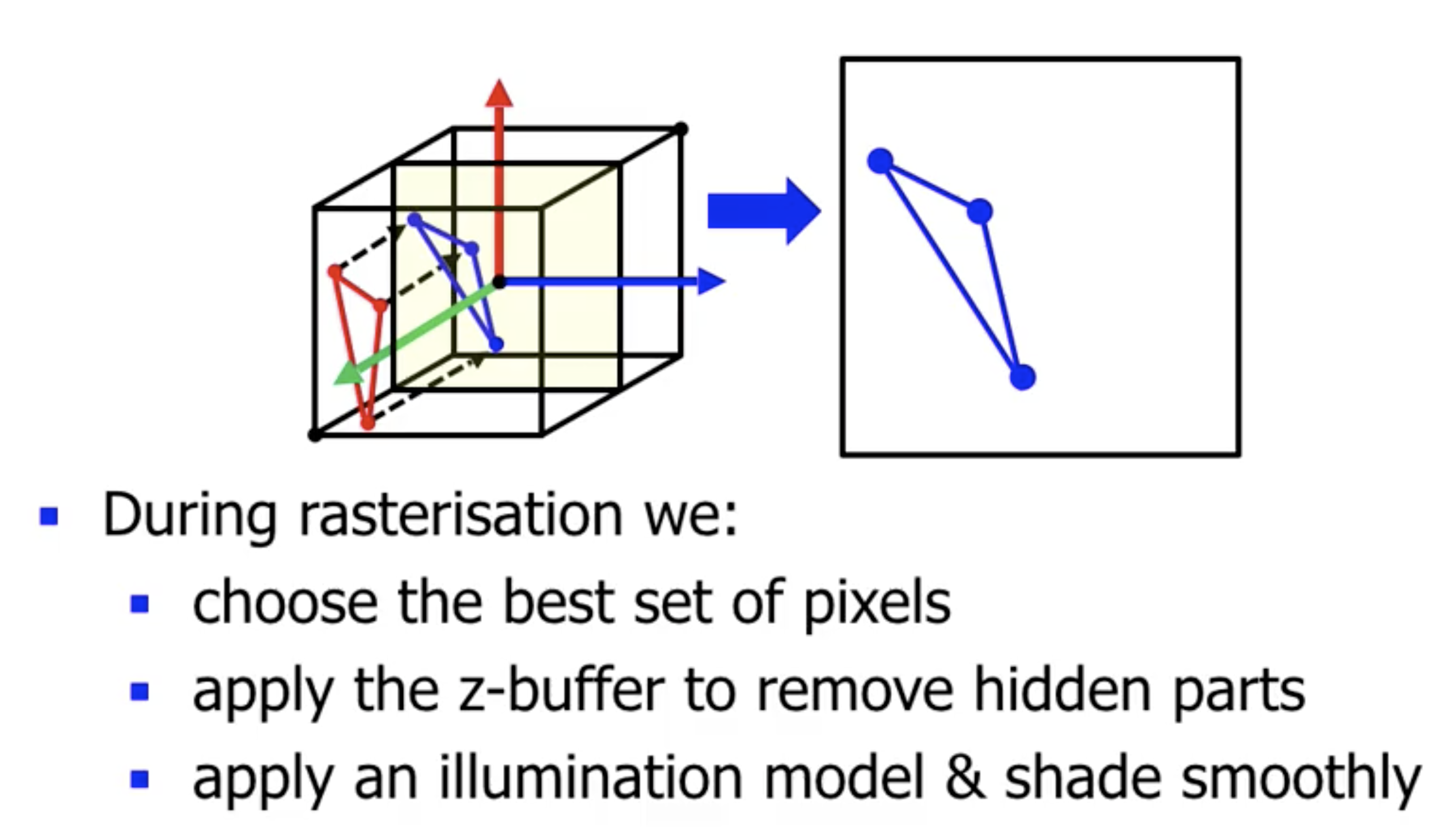
在 ThreeJS 中, 光照模型和上色方式的选定 被封装在声明三维物体时的 材质选择 中:

光照
对光照的建模有两种常见方式: 局部光照模型 和 全局光照模型, 其中前者只考虑由某个空间中的独立光源对模型的照射结果, 而后者在此基础上还要同时考虑 光线反射, 折射 以及 物体之间相互干涉 的作用.
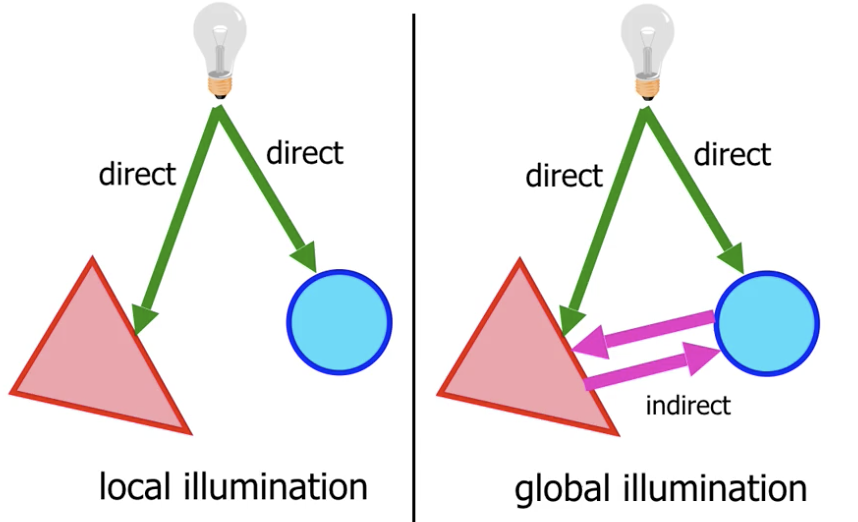
在本课程中, 我们讨论简单的 局部光照模型.

由于现实世界中的光照是极其复杂的, 我们在计算机图形学中建模光照时永远考虑的是现实情形中的 近似.

反射
举例而言, 在实际情况下 由于任何物体表面都不可能完全不透光, 因此光线照射到物体表面时, 会 穿过物体表面薄薄的一层, 并照射到色素粒子上, 构成一些经过干涉产生的漫反射光.
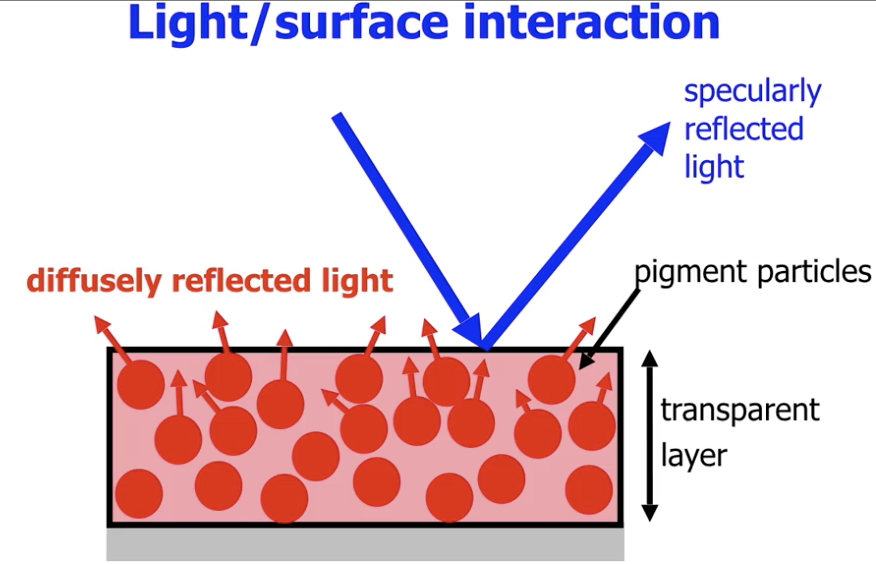
因此, 漫反射可以被视为 物体表面吸收部分波长的光 并 将剩余的光均一辐射 的结果:

它的特征就是, 光线照射到物体表面后会向 所有方向 传播:
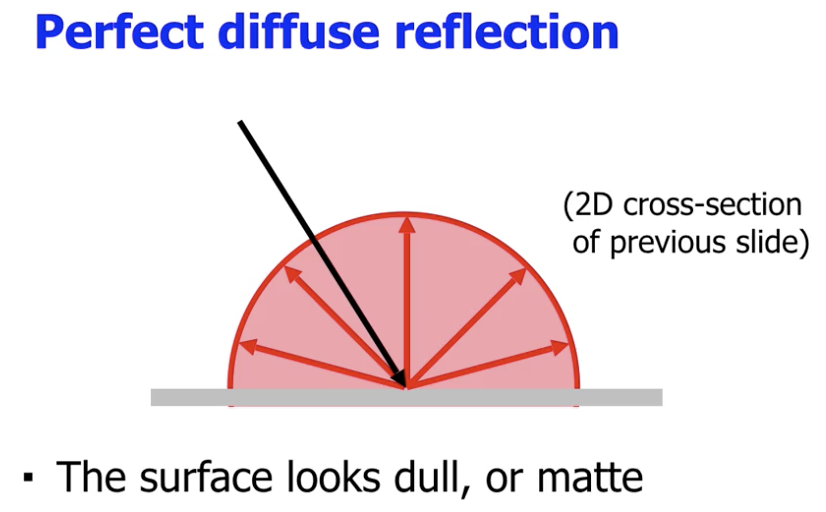
而镜面反射则可被视为是光在物体和空气界面交界处产生的反射.

而在实际情况中, 镜面反射还被进一步细分出 完美镜面反射 和 不完美镜面反射:
完美镜面反射基本只在 理想条件下 发生, 此时入射光打到 完全平滑 的表面上, 因此被直接反射出去, 入射角和反射角恰好相等.
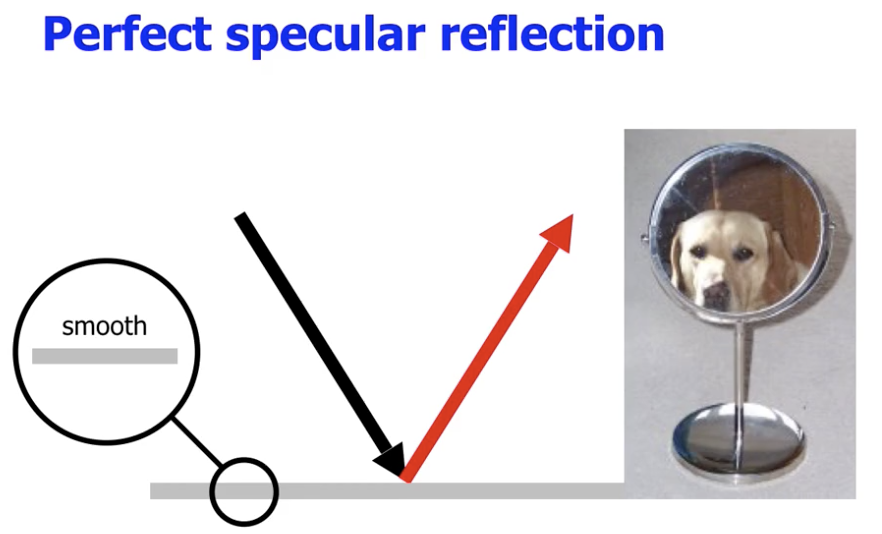
而在实际情况中, 由于任何平面总是会存在一些不规则的坑洼, 而不可能完全平滑, 因此发生的实际上是反射角度 有略微不同 的 不完美镜面反射:
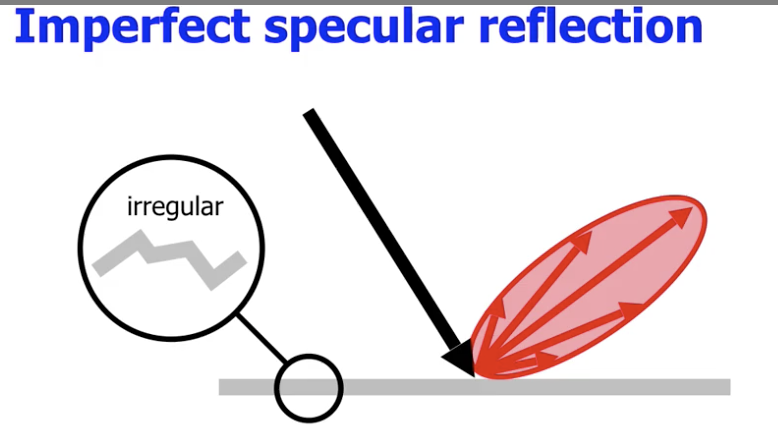
建模漫反射 (Diffuse Reflection)
下面我们考虑对 漫反射 的建模. 我们同时考虑三种不同的光源: 环境光 (Ambient Illumination), 无穷远的点光源 (Directional Illumination) 和 场景中的点光源.
首先, 由于已知漫反射过程中存在对入射光的部分吸收, 我们可以近似认为在不考虑颜色的情况下, 入射光在物体表面发生漫反射后的反射光 光强有所降低. 因此我们使用系数 $k_a$ 控制漫反射光被削弱的强度:

由此我们就得到了最简单的第一版局部光照模型.

由于在该模型中物体的每个面的漫反射系数相同 (因为材质相同), 因此得到的渲染结果中自然每个面的亮度都是相同的.
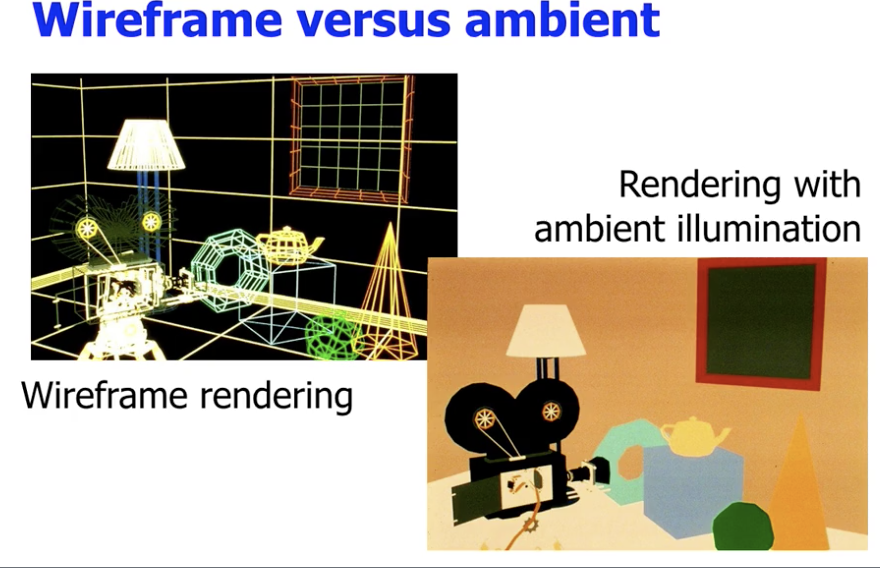

下面我们进一步考虑 有向光照 (Directional Lighting), 也就是点光源.
在对点光源进行建模时, 我们可以考虑的主要参数包括:
- 光照强度随距离光源远近的衰减
- 光线入射角随距离光源远近的变化
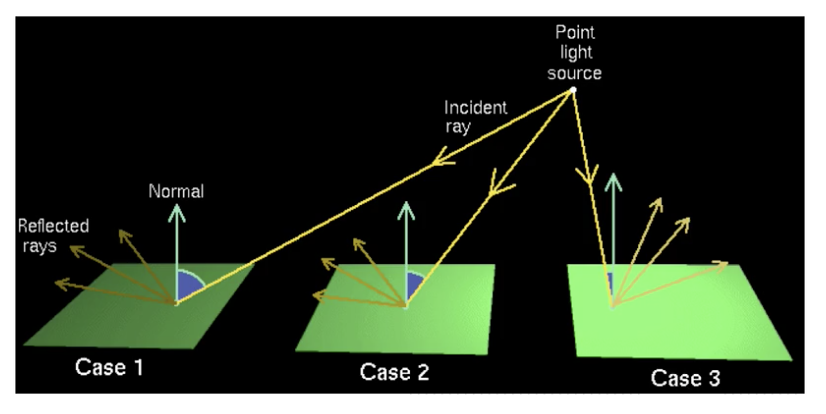
由此我们可以进一步确定在不同情况下点光源照射有颜色物体后, 该物体实际表现出的颜色应该是什么.
我们首先对漫反射中 入射角 的作用进行建模.
考虑下列模型:
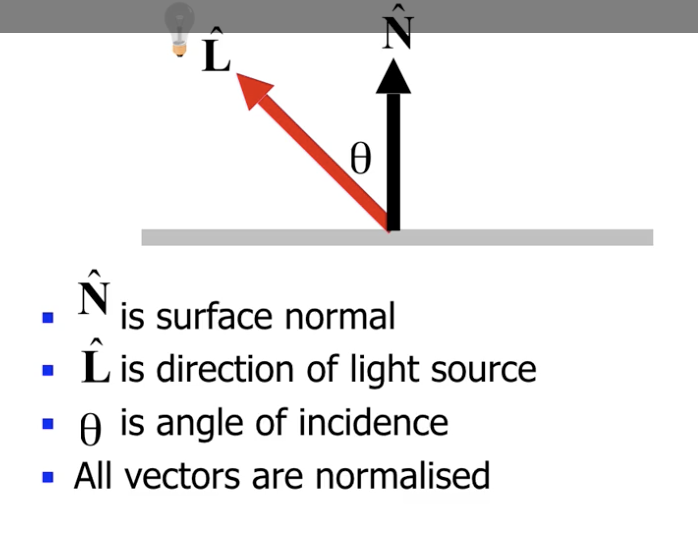
我们希望对 入射光打到平面上时, 平面所接受的实际光强 和 入射角度 之间的关系建模. 此处的建模方式是直接利用漫反射中的一个结论: Lambert's Law:
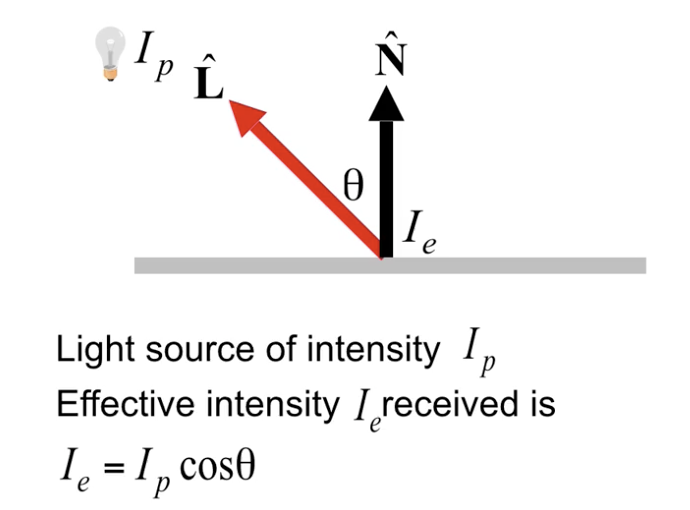
在入射角为 $\theta$ 时, 平面所接受的实际光照强度是 $I_p \cdot \cos(\theta)$, 这是由于光线倾斜射入平面的一段范围 $x‘$时, 实际上真正射入的光线只在 $x = x’ \cdot \cos(\theta)$ 内, 由于光线数量少了 (更科学的说法应该是光子数量, 因为实际上并不存在光线), 因此光强等比例减少. 当范围 $x$ 趋于 $0$ 时, 就得到了该定理的结果:
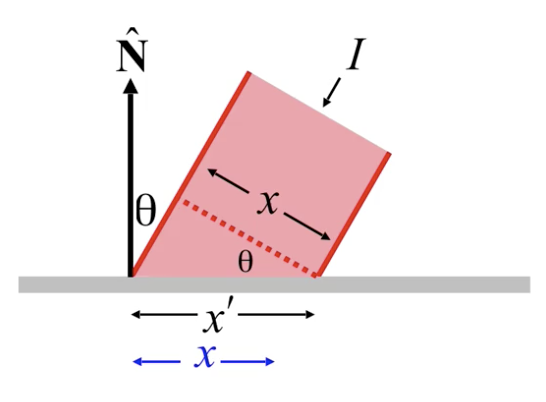
同时我们为 漫反射中从物体表面反射出的光强 进行建模, 假定它受参数 $k_{d}$ 控制.
由于我们知道 表示入射光和平面法线 的 单位 向量 $L$ 和 $N$ 点乘结果为 $L\cdot N \cdot \cos(\theta)$, 因此点光源对物体产生的漫反射光强就可表示为
\[I_{\text{diffuse}} = I_p \cdot k_d \cdot(N \cdot L).\](因为 $N, L$ 都是单位向量, 所以 $N\cdot L = \vert N\vert \cdot \vert L \vert \cdot \cos(\theta) = \cos(\theta)$.)

由此我们就得到了第二版 由环境光和局部光照产生的漫反射 组成的局部光照模型:

而和我们的第一版模型相比, 可见在真实性上新版模型有了长足的进步.

我们最后考虑光强随光的传播距离而衰减的问题. 基于基本物理知识可知, 光强随传播距离的衰减关系满足:
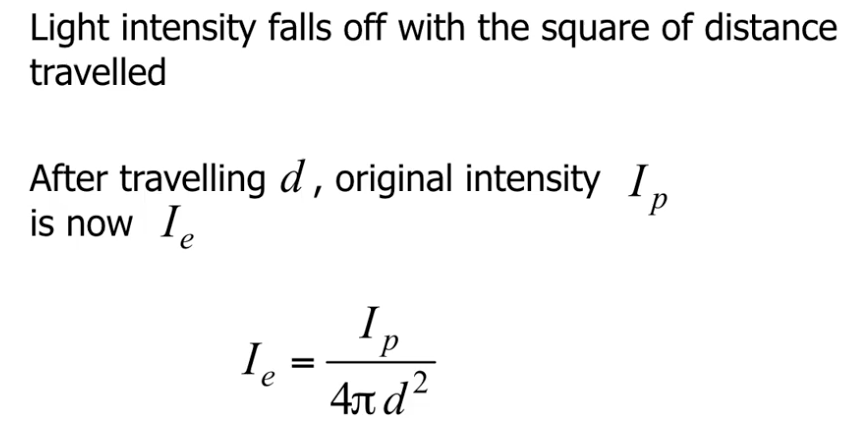
但需要注意的是, 由于 $d^2$ 变化速度太快, 因此在实际情况下分母都使用 二次多项式 拟合, 多项式的系数被视为需要调整的超参数.
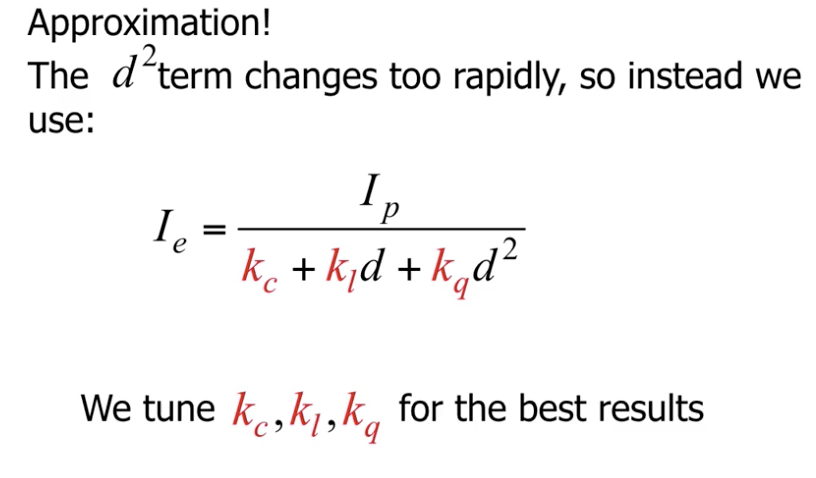
因此在进一步考虑点光源光强的衰减效果后, 我们得到了第三版局部光照模型:

建模镜面反射 (Specular Reflection)
下面我们在第三版局部光照模型的基础上考虑对镜面反射的建模.
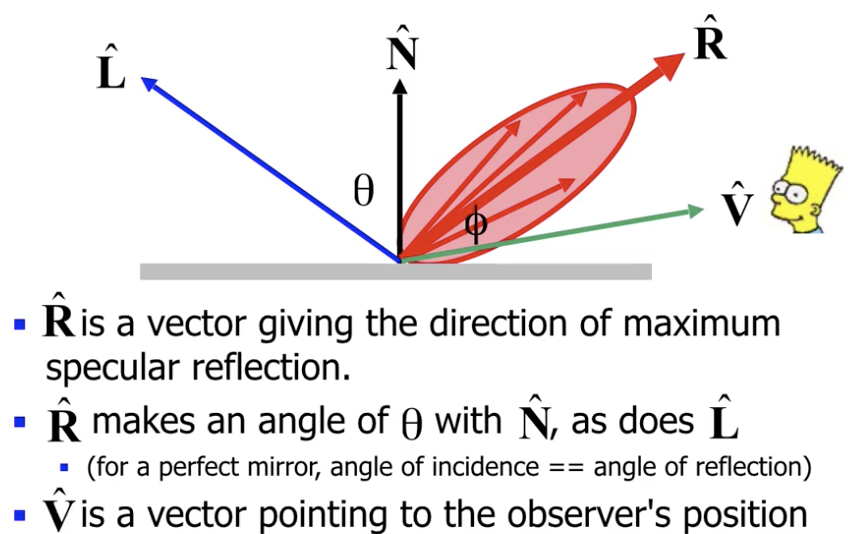
首先考虑 不完美的镜面反射. 基于现有知识, 由于不完美镜面反射由多个反射角 大于, 等于或小于 入射角的反射光组成, 因此观察者看到的实际光强 和观察者的角度相关, 此处我们认为其中一个影响因素是 观察者的观察方向和完美反射光之间形成的夹角 $\phi$.
同时, 观察者观测到的反射光强显然还和 入射光强 以及 入射光的波长 相关, 因此在我们的建模中认为 观察者观测到的不完美反射光强 和 观察方向与完美反射光方向之间的夹角, 入射光强和光的波长 相关.

我们首先观察观察到的光强和观察角度的影响. 我们将在不同角度上观察反射光所接收到的光强和观察角度 $\phi$ 的关系 使用 $\cos^{n}(\phi)$ 拟合:
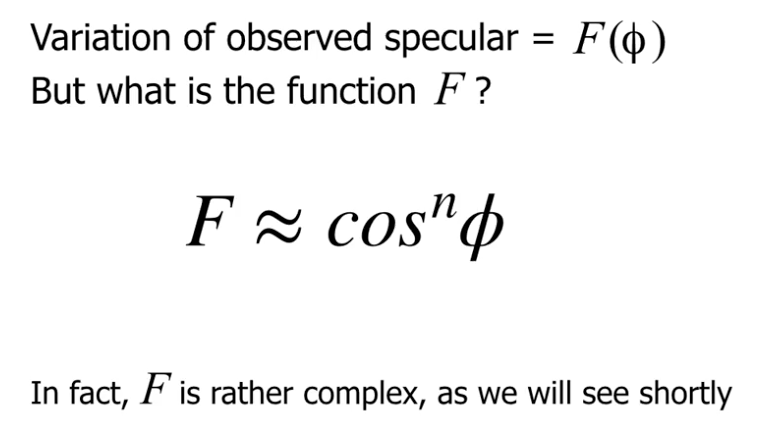
因此有:

我们然后考虑光线波长的影响. 由下图可见, 实际情况是极其复杂的, 对其进行完全一致的建模基本上是一件不切实际的事情.
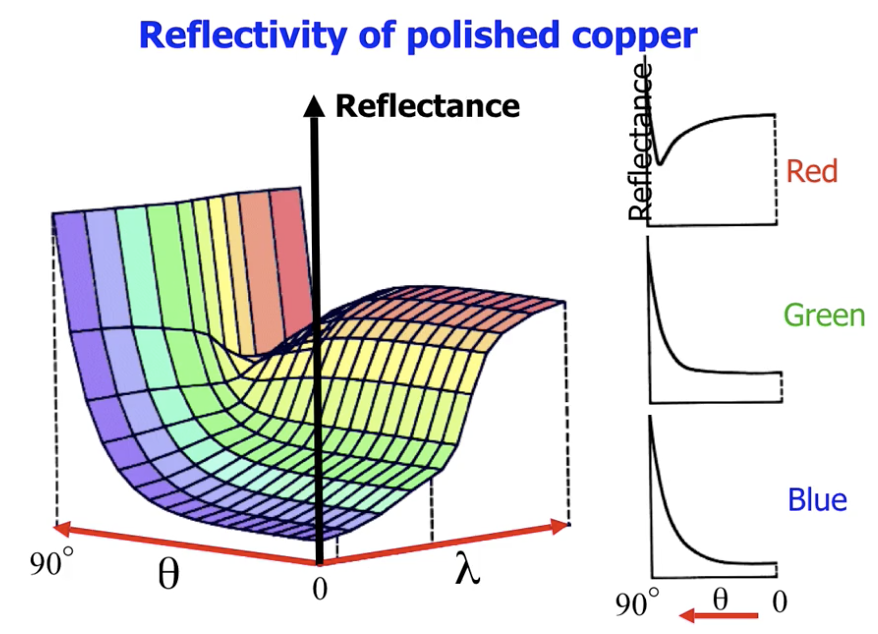
由于反射光强和入射角相关, 因此我们基于 菲涅尔定律 对剩下的两个参数: 入射角和波长进行建模:
菲涅尔定律的一个重要结论是: 任何物体都具备一个描述其 光线折射能力 的系数 $\mu$: Refractive Index. 而记 $\theta$ 为折射角, $\phi$ 为入射角, 则有:
而进一步地, 折射系数 $\mu$ 又和 光的波长 相关.

因此进一步地我们就可以将 $F$ 近似为 镜面反射系数 $k_{s}$. 此时有:

其中 $R\cdot V$ 是 观测方向和反射光线之间的夹角. 由此我们就得到了第四版本的局部光照模型, 它同时考虑了环境光源, 点光源对物体造成的漫反射以及点光源对物体造成的镜面反射的影响.

可以看出第四版局部光照模型相比未考虑镜面反射的第三版模型更贴近真实情况.
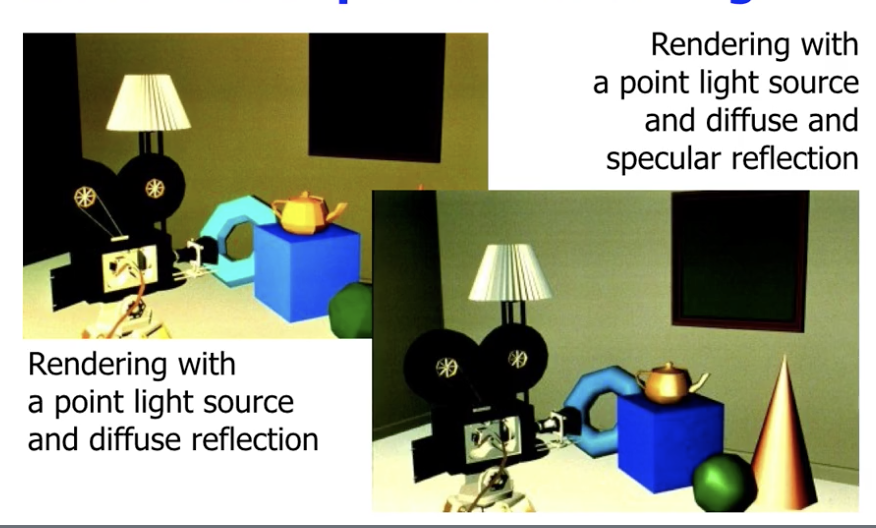
最后, 我们对三原色中的每个颜色通道均应用局部光照模型, 就实现了 颜色的引入.

注意:
- 环境光漫反射系数 $k_a$ 和局部光漫反射系数 $k_d$ 因颜色通道而异!
- 镜面反射系数 $k_s$ 不受颜色通道影响!
通过结合颜色, 我们就得到了第五版局部光照模型:

而在需要考虑 多个点光源 时, 只需将点光源的作用效果 叠加 即可:

着色
在得到局部光照模型后, 我们下面考虑 如何对网格 (物体表面) 上色 的问题.
Flat Shading
Flat Shading 又称 Constant Shading, 在着色时, 使用 该面的法线 结合光照模型计算颜色, 然后将这个颜色 应用在整个面上.
因此同一个面中所有像素的颜色均相同, 我们可以明显观察到网格之间的差别.
同时由于 马赫带效应, 在人类的观察中不同颜色表面的交界 比实际更明显, 因此可以观察到令人感到不适的割裂感.

Gouraud Shading
Gouraud Shading 使用 插值 尝试 模糊化面法线不同的面之间颜色的区别, 减少割裂感.
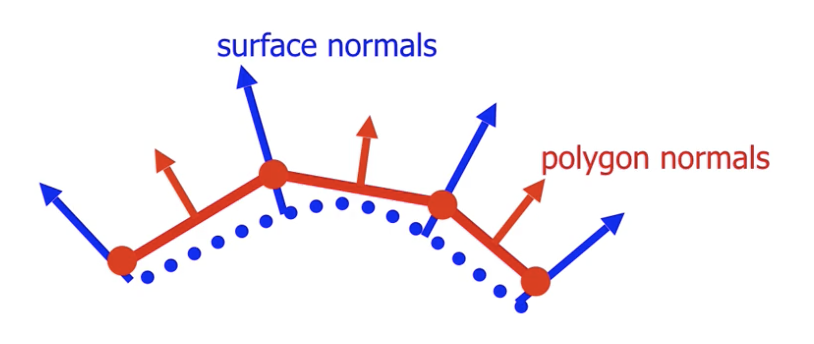
其中, 网格中每个顶点上的曲面法线实际上是 包含这个顶点的所有相邻面 的 曲面法线的平均:
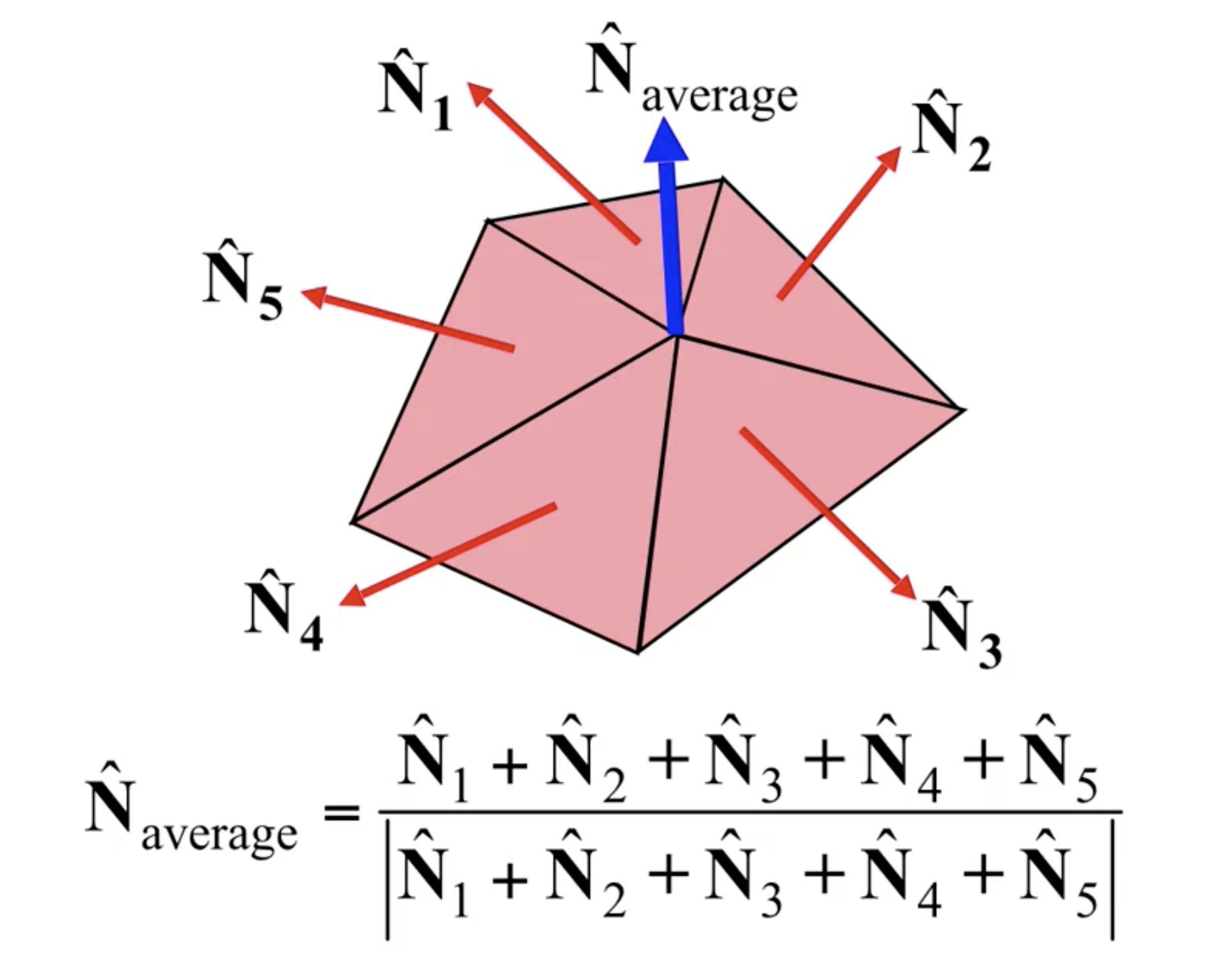
如上图所示, 中间的顶点和五个面临接, 因此该顶点的曲面法线就是这周围五个面的曲面法线的平均.
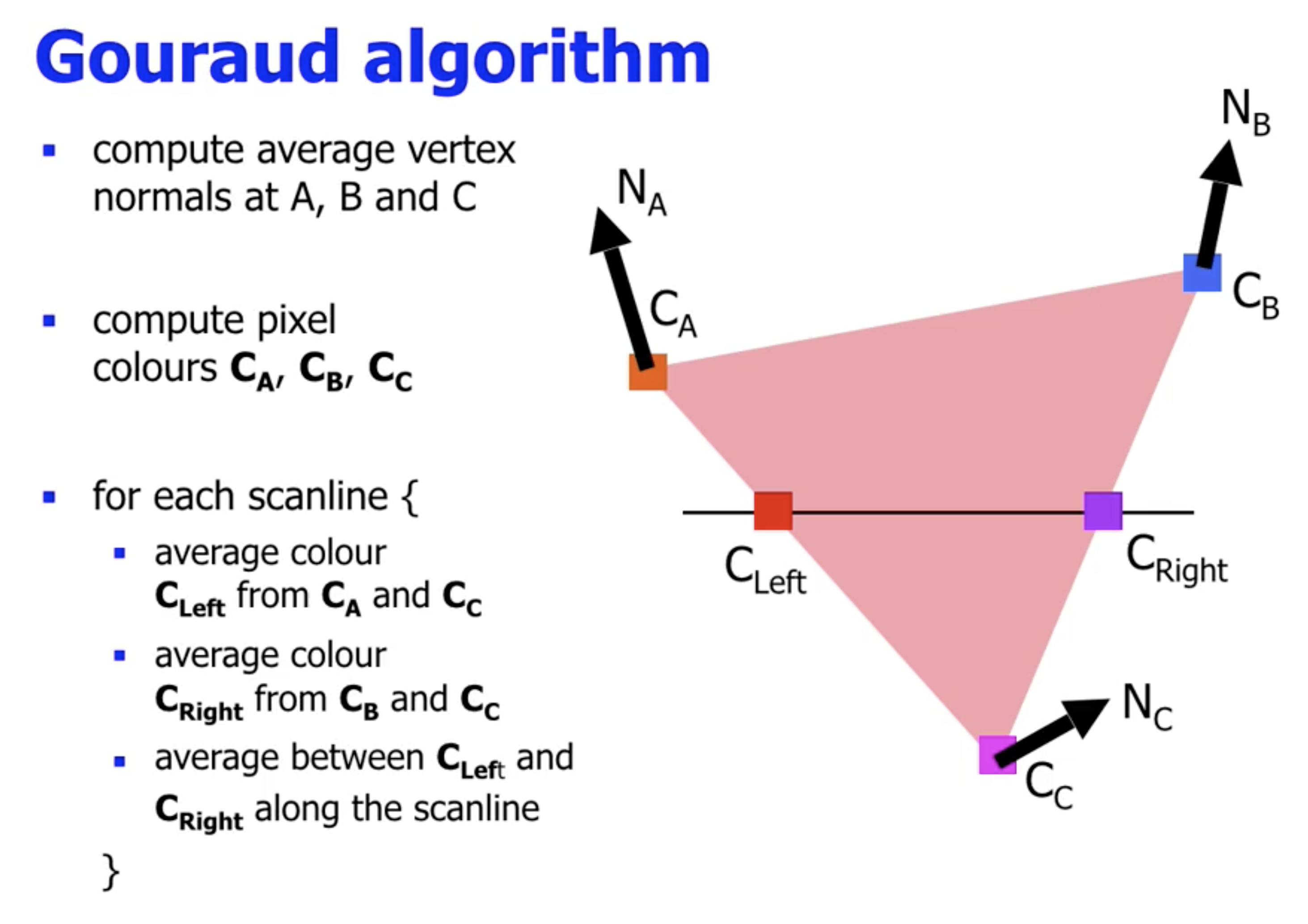
因此 Gouraud 算法对面上每个像素颜色的近似过程就是:
考虑最一般化的三角形面 (更复杂的面可以通过曲面细分表示为多个三角形面), 三个顶点处的对应曲面法线分别为 $N_A, N_B, N_C$, 基于曲面法线应用局部光照模型计算出的颜色分别为 $C_A, C_B, C_C$.
- 假设平滑方向是自左向右, 首先分别关于左侧边 $AC$, 基于顶点颜色 $C_A, C_C$ 计算出该边上每个位置对应的 平均颜色 $C_{\text{left}}$ 的表达式.
- 其次关于右侧边 $BC$, 基于顶点颜色 $C_B, C_C$ 计算出该边上每个位置对应的 平均颜色 $C_{\text{right}}$ 的表达式.
- 然后 自左向右扫描, 沿着从左向右的扫描线, 依次在线上基于该线的 $C_{\text{left}}$ 和 $C_{\text{right}}$ 对线上的颜色进行平均.
可以看到, Gouraud Shading 起到了相对良好的平滑效果:

注意到在每一条扫描线上, 颜色随着像素位置的递增变化值是 不变 的. 因此在实际实现中, 一种性能优化方法就是: 不去分别计算每个像素点上的颜色, 而是从最左侧的颜色开始, 基于每个像素点的位置不同将对应位置上的颜色以 “base+offset” 的方式累计计算, 这样可以减少计算量.

虽然 Gouraud Shading 效率很高, 但它仍然存在两个主要问题:
- 它在一些情况下可能 会将镜面高光平滑掉.
- 它在一些情况下可能将 不该被平滑的边缘平滑掉.
Phong Shading
Phong Shading 和 Gouraud Shading 的不同之处在于: Gouraud Shading 直接基于顶点的颜色 对 颜色进行平滑, 而 Phong Shading 先平滑法线向量 (Normal Vector), 然后再 基于法线向量分别计算每个像素的颜色.
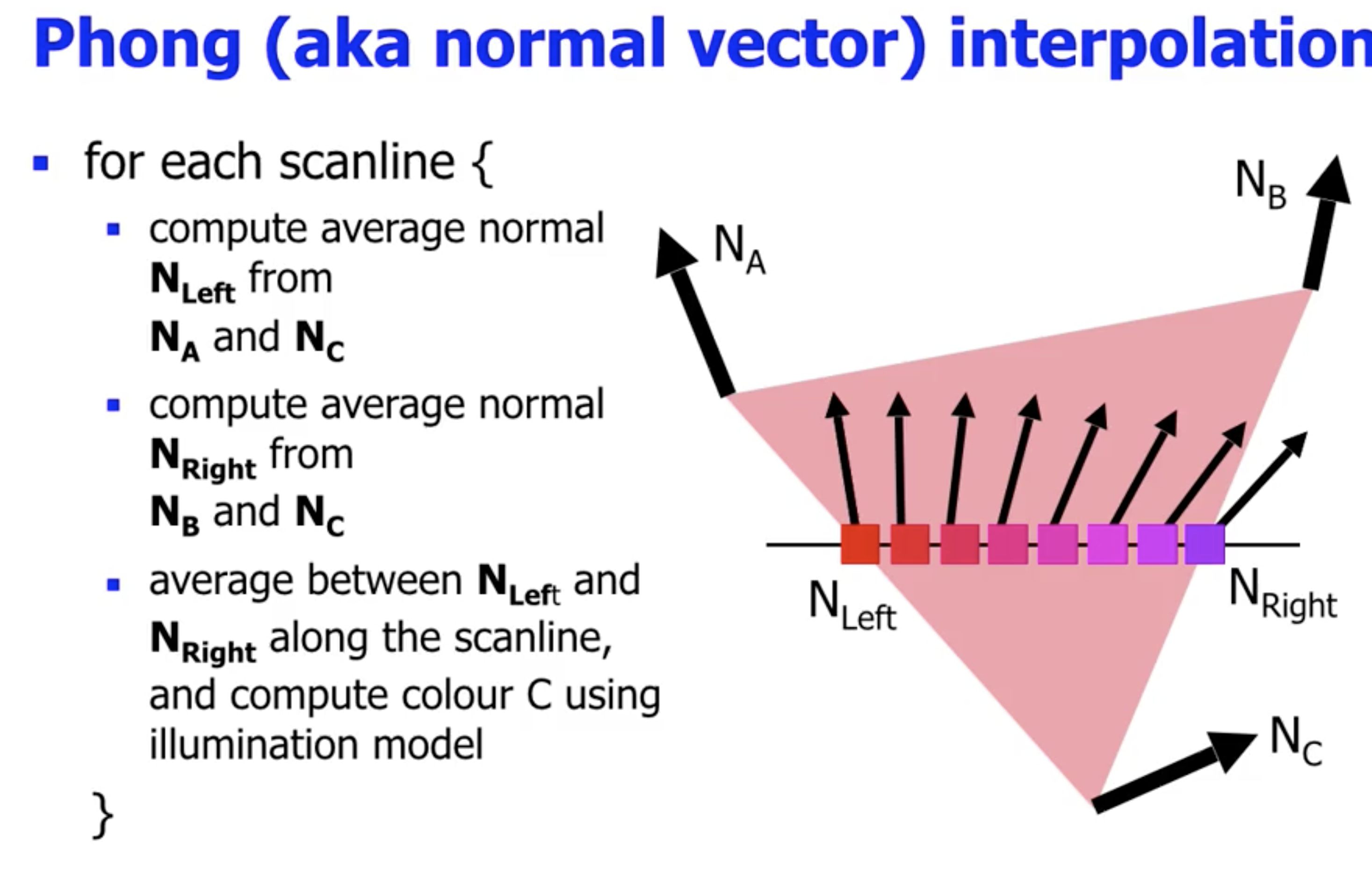
因此 Phong Shading 也被称为 法线向量着色 (Normal Vector Shading). 显然此处我们也可以类比 Gouraud Shading, 同样使用 “Base + Offset” 的方式计算每条扫描线上每个像素对应的法线向量, 减少计算次数.
最后, 从横向对比中可以看出, Phong Shading 相比其他两种更简单的着色方式保留了更多应有的细节, 更加贴近真实情况.

值得关注的是, 由于 Phong Shading 中在计算网格中每个像素的颜色时都需要基于该像素对应的法线向量代入光照模型计算颜色, 因此它相比直接对颜色进行平滑的 Gouraud Shading 需要的计算量 明显更大.

贴图
我们最后讨论 纹理贴图 (Texture Mapping) 和 凹凸贴图 (Bump Mapping).
纹理贴图
利用纹理贴图的方法主要分为两种: Image-based, 将 表示纹理的图片直接映射到三维物体表面, 或 Procedural, 基于一定的规则 动态计算 出物体表面对应位置的纹理.

在本课程中, 我们只介绍第一种纹理贴图方法.
利用纹理贴图的第一步是 定义纹理. 在此我们简单地将表示物体纹理的图片理解为纹理贴图. 和像素一样, 纹理贴图中最小的组成单位被称为 Texel (纹素), 而我们引用纹理贴图中纹素的方式和我们引用位图中像素的方法一致, 都是通过 “建立坐标系 - 使用坐标引用” 的方式实现的. 一般地, 纹理贴图中坐标轴分别使用 $U, V$ 表示.

而 纹理映射 (Texture Mapping) 就是将 纹理贴图映射到多边形面上 的过程.
考虑最简单的 “Texture-per-Polygon” 映射, 其流程就是: 基于多边形顶点坐标找到纹理贴图中的对应坐标 $T(u,v)$, 然后和 Gouraud Shading/Phong Shading 中对颜色/法线的平滑逻辑一样, 我们可以得到每条扫描线上对应位置的纹理贴图坐标, 从而就可以对 多边形上每个像素 绑定 纹理贴图中对应位置的纹素.
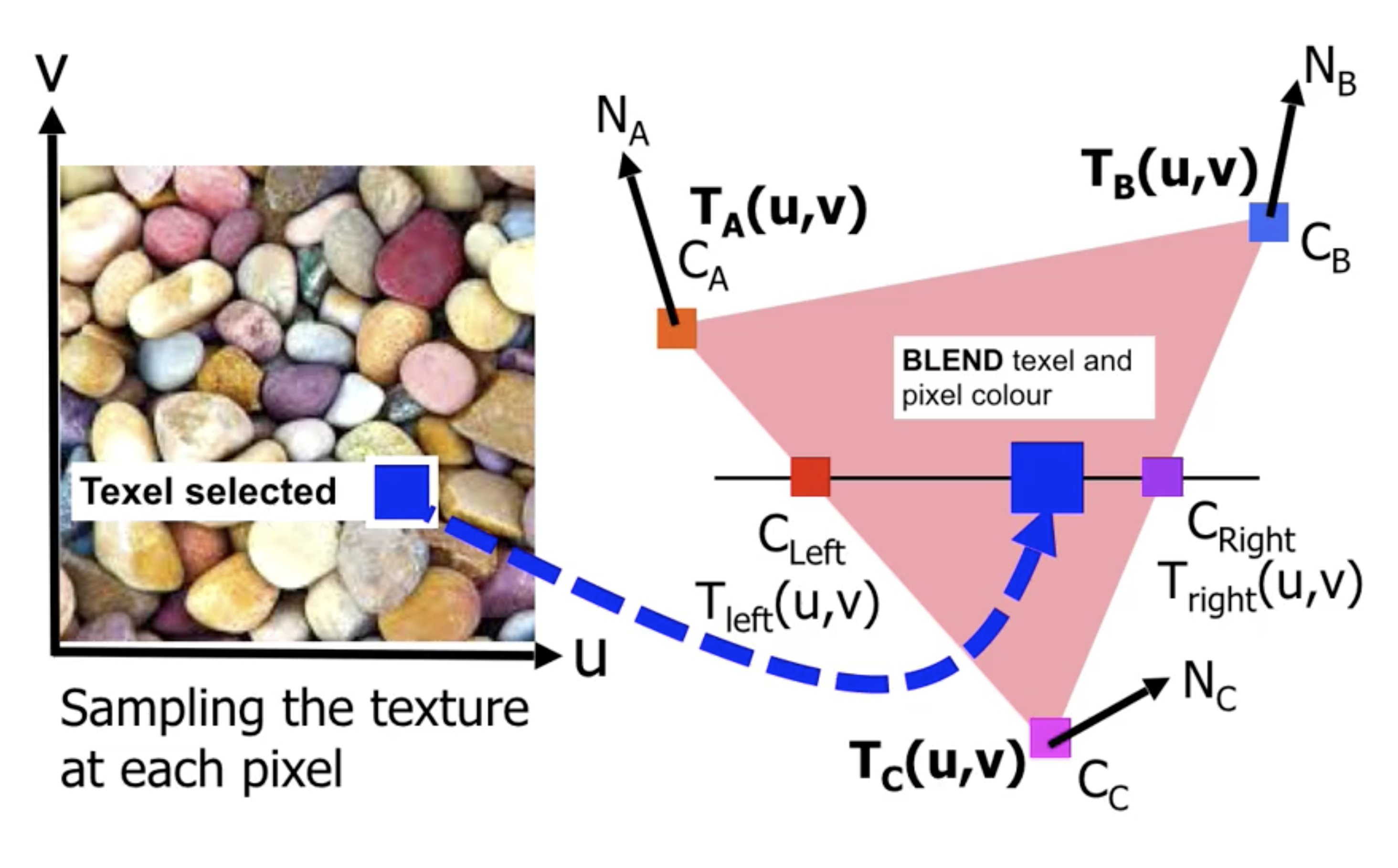
接缝问题
而在现实中, 上述实现存在明显的问题. 首先如果纹理选择不当的话, 就可能在渲染结果中看到明显的 不一致的接缝 (Seams):

因此 如果多个连续的多边形要使用同样的纹理, 还需要确保纹理可以 无缝拼接, 否则就会出现视觉上不一致的接缝.
分辨率不一致问题
此外, 在纹理贴图分辨率和多边形分辨率 不一致 时, 为了确保合理的视觉效果就 不能直接进行映射.

分辨率不一致的问题可以被细分为两种情况:
像素分辨率大于纹理分辨率
考虑像素分辨率大于纹理分辨率的情况, 原则上 多个不同像素就会被映射到同一个纹素上. 因此我们可以选择 不做任何处理, 也可应用 双线性插值过滤法 (Bilinear Interpolation Filtering).

无过滤
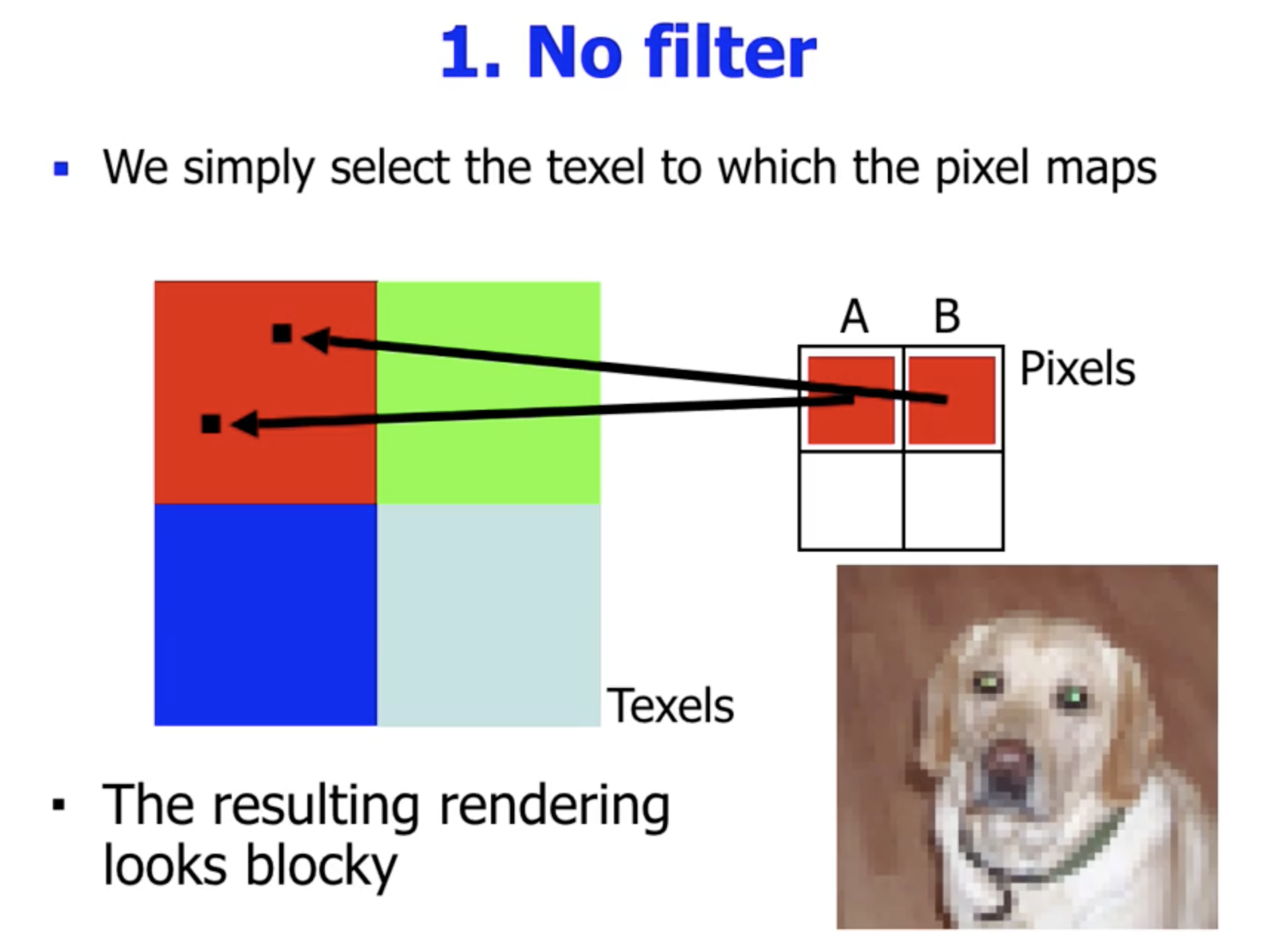
此时由于纹素实际上被未经插值地直接等比例放大到更高分辨率的面上, 因此得到的结果会有明显的马赛克化, 不清晰.
双线性插值过滤
在双线性插值过滤中, 每个像素的颜色实际上是 分数坐标 (Fractional Coordinate) 表示下最近邻居纹素颜色的平均:
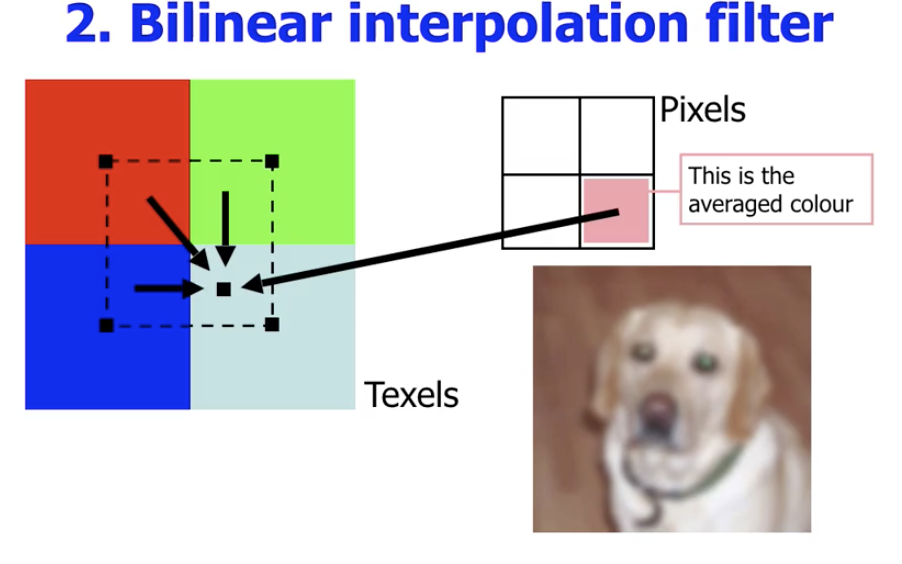
此时由于纹素被插值放大, 因此得到的结果会显得模糊, 但更加平滑.
像素分辨率小于纹理分辨率
考虑像素分辨率小于纹理分辨率的情况, 此时只有 一部分纹理贴图 可被映射到多边形上. 如果直接映射的话, 相邻的像素就会被映射到 不相邻的纹素 上, 导致 aliasing.

由于此处涉及到纹理贴图的语义问题, 因此原则上没有全自动的处理方式, 合适的解决方法是使用 Mipmap Filtering: 利用人眼 看不清远处物体细节 的特征构造出一系列 包含信息逐渐减少 的 尺寸不一 的纹理贴图, 这样在需要将纹理贴图映射到低分辨率的多边形上时, 我们就可以直接选择分辨率一样低的贴图.
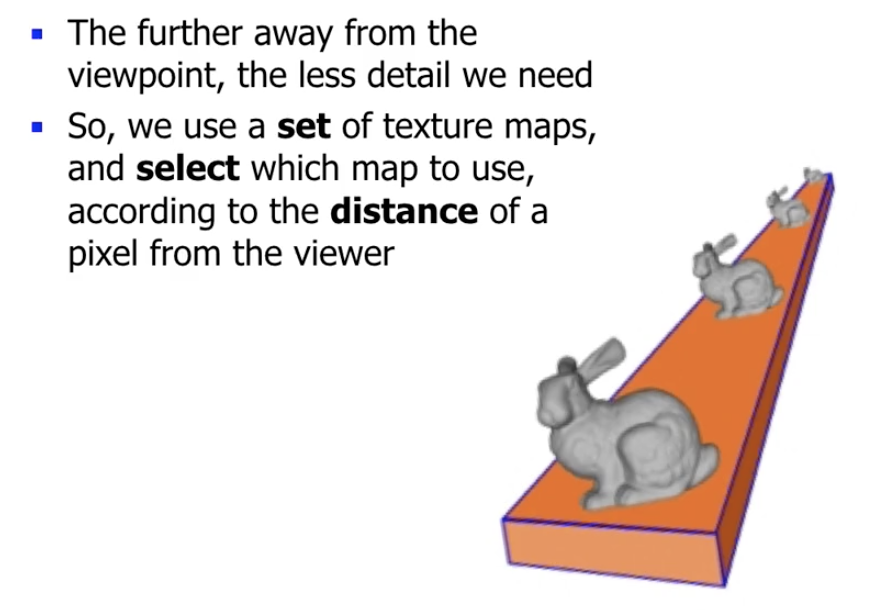
(The origin of the term mipmap is an initialism of the Latin phrase multum in parvo (“much in a small space”)”)
而构造这一系列不同分辨率的纹理贴图的方式就是 Subsampling, 用合适的方式令它们包含的语义和细节依次减少.

而其存储空间的消耗实际上相对不多: 占用的空间只是分辨率最大的贴图 $t_0$ 的两倍.

纹理贴图的其他用处
此外我们还可以使用纹理贴图构造光照效果, 保存光照信息的纹理贴图被称为 Lightmap.

凹凸贴图
我们下面考虑使用凹凸贴图模拟 凹凸不平的表面.
从常识来看, 光在凹凸不平的表面上的反射效果不同, 因此可以通过使用 凹凸贴图 存储 对表面不同位置上法线向量的偏移 使表面的法线向量 经过人为偏置之后和原来不同, 进而在经过光照模型处理后具有 不一致的光照效果, 产生表面凹凸不平的错觉.
要影响法线向量, 最实际的方式就是构造一个由平面坐标轴方向向量 $u, v$ 乘上对应缩放系数 $b_u, b_v$ 合成的偏置向量 $b_uN_u + b_vN_v$ (回顾: 贴图中的横纵坐标一般用 $u, v$ 表示, 而且此处的 $N_u, N_v$ 是单位方向向量), 使最终得到的, 经过偏置的法线向量是 原法线向量和偏置向量的合成.
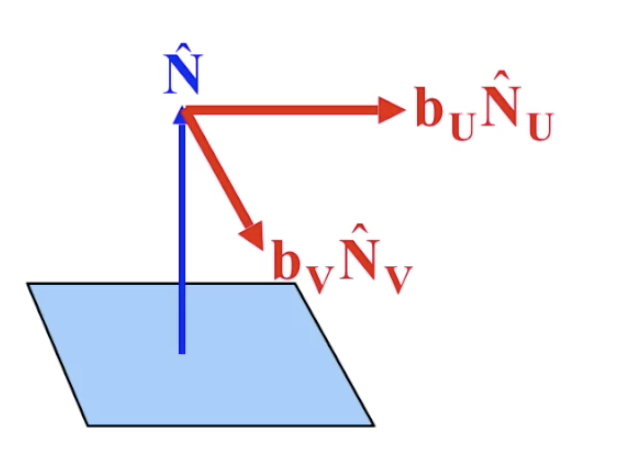
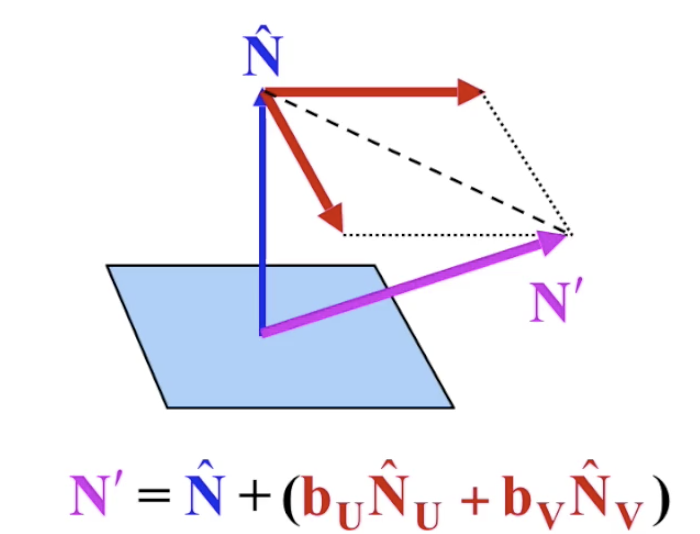
因此我们就需要对每一个像素存储对应的偏置系数: $b_u, b_v$. 一种可行的计算方式是基于纹理贴图中 对应纹素颜色和其邻居颜色的差别梯度计算:

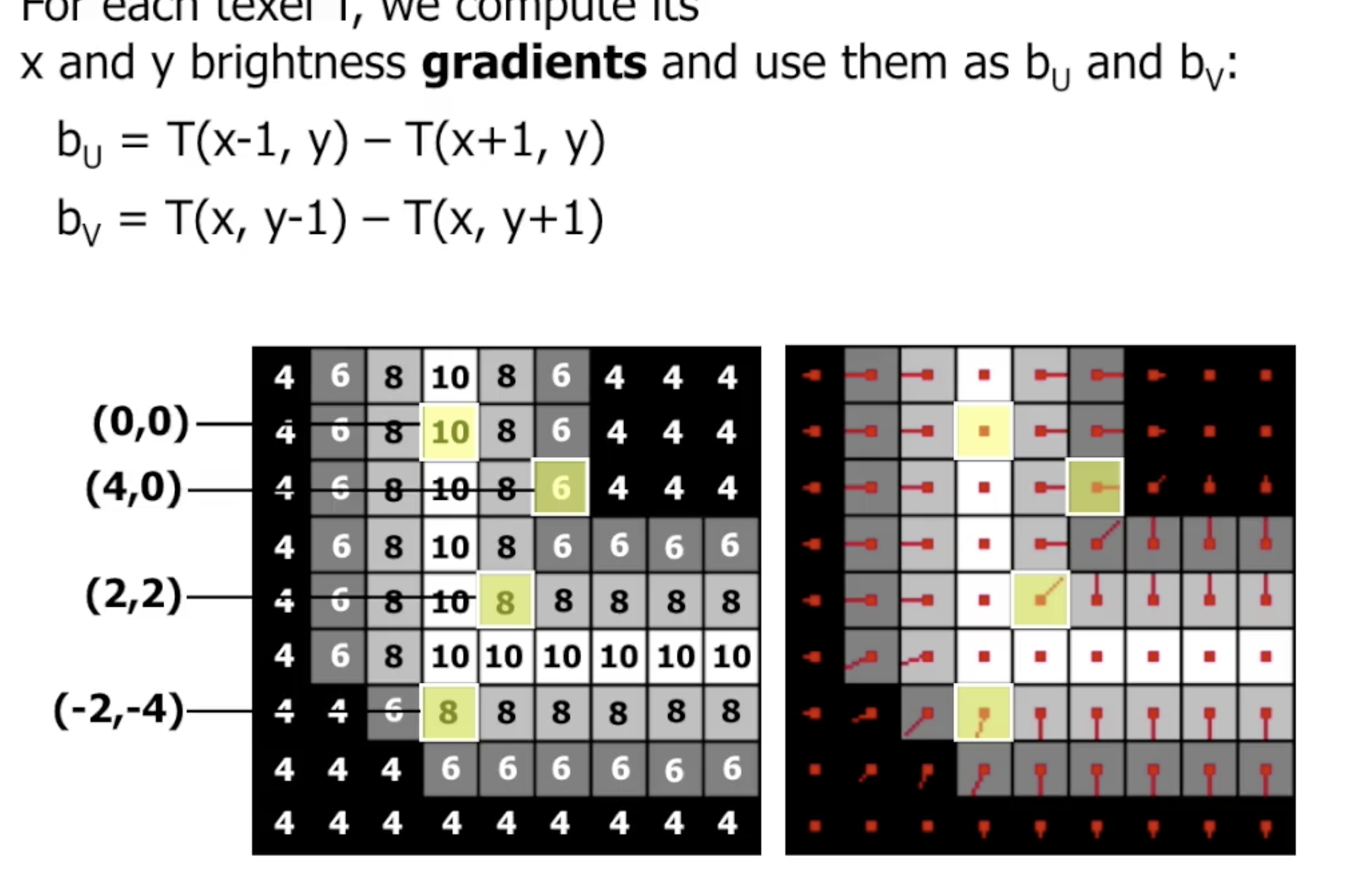
最后总结: 在本课程中, 我们介绍了图形管线的基本结构, 基本了解了如何使用 API 对图形管线进行控制, 并详细从零开始初步分析了图形管线中 基本形状的表示和构造, 图形变换和视角变换 的类型, 表示方式, 计算方式与合成方式, 基于 二维和三维平行/透视视角 将三维空间映射到显示屏上的计算方法, 对 不同光照和反射 的建模, 不同类型纹理贴图 的定义和应用, 以及 在此基础上对图形进行渲染 的全部流程和步骤.
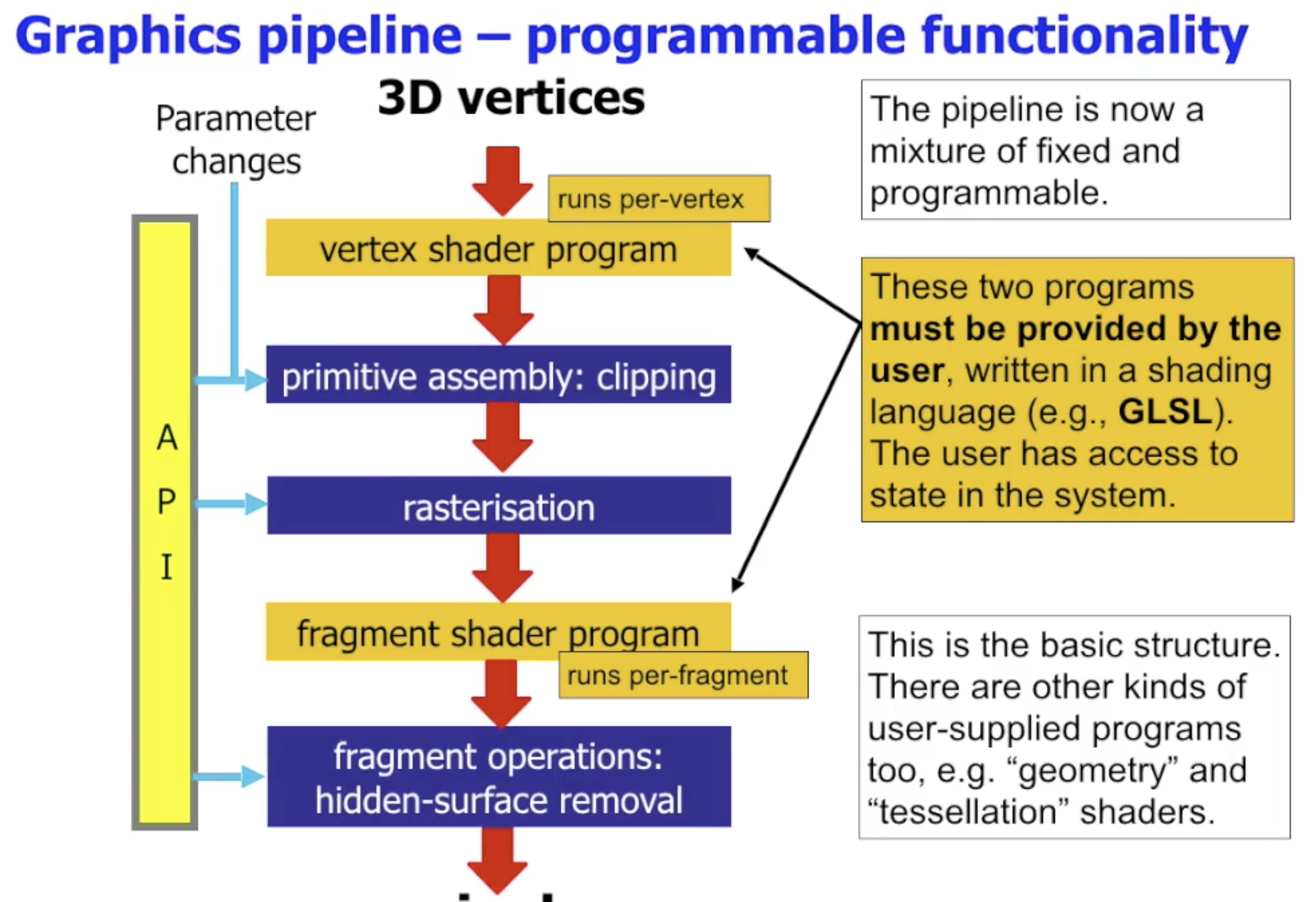
最后回顾图形管线的基本组成. 如果到此你还不能完整地回忆出图形管线的主要操作组成和图像处理流程的话, 建议你赶紧回头把前面的笔记全部看一遍, 或者选择明年重修这门课程.
