编译器引论
任何使用程序设计语言编写的计算机程序在被实际执行前都必须 转译为机器语言, 而负责这一转译过程的软件系统就是 编译器 (Compiler).
在本章中, 我们将简要介绍 编译 流程的基本原理和技术, 并简单讨论在构造编译器时可能遇到的一些常见问题.
1. 绪论
定义
我们首先为 编译器 的概念给出形式化的定义.
一种说法是, 任何接收一种一段程序字段作为输入, 并以另一种语言的程序字段作为输出, 且输入和输出的含义保持一致的程序就被称为 编译器.
我们也可认为, 任何读入用一种语言编写的程序, 并将其翻译为另一种语言下的等价形式的程序也是 编译器.
而 解释器 的概念为: 任何读入一段 源程序 (Source Program) 并产出 执行这段源程序的结果 的程序.
必须使用 编译器 才能生成可被直接运行的可执行文件的程序设计语言被称为 编译型语言, 如 C/C#/C++, Java 和 LaTeX.
而无需编译可被解释器直接运行的语言称为 解释型语言, 如 Python, PHP, JavaScript 等.
应用
编译器作为衔接两种不同语言之间的桥梁, 其最基础的功能就是 在翻译过程中确保程序所含的语义 (意义) 保持不变. 而在实际情况中, 编译器往往还承担了对源代码进行 (各种意义上的) 优化的功能, 如:
- 提升编译后的程序的运行速度
- 减少编译后的程序的占用空间
- 向用户提供有价值的反馈和信息
- 在编译失败时能够返回便于调试的错误信息
- 以较高的效率编译源码
而一般地, 我们认为优秀的编译器至少需要具备下列的其中一些特质:

实际上, 编译技术的应用场景不仅局限在对程序设计语言的转换上. 它还可用于优化计算机机构, 实现自动的并行式计算, 提升软件安全性等.
基本结构
下面我们考虑编译器的基本结构.
我们在上面的介绍中已经知道, 编译器以 源代码 (Source Code) 作为输入, 将其转换输出 目标代码 (Object Code). 因此, 正常工作的编译器需要具备的最基础性质是:
- 生成的目标代码必须是正确的, 保持源代码的语义不变.
- 必须具备识别源代码中错误的能力.
- 必须具备对源代码进行分析与合成目标代码的能力.
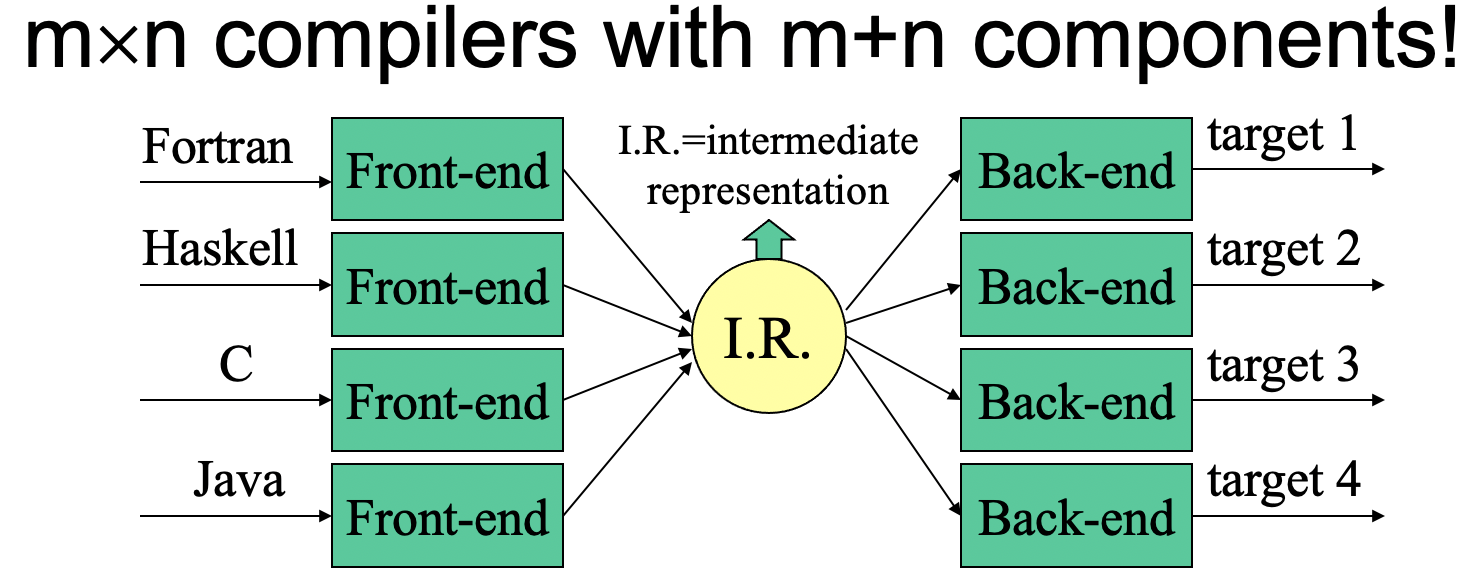
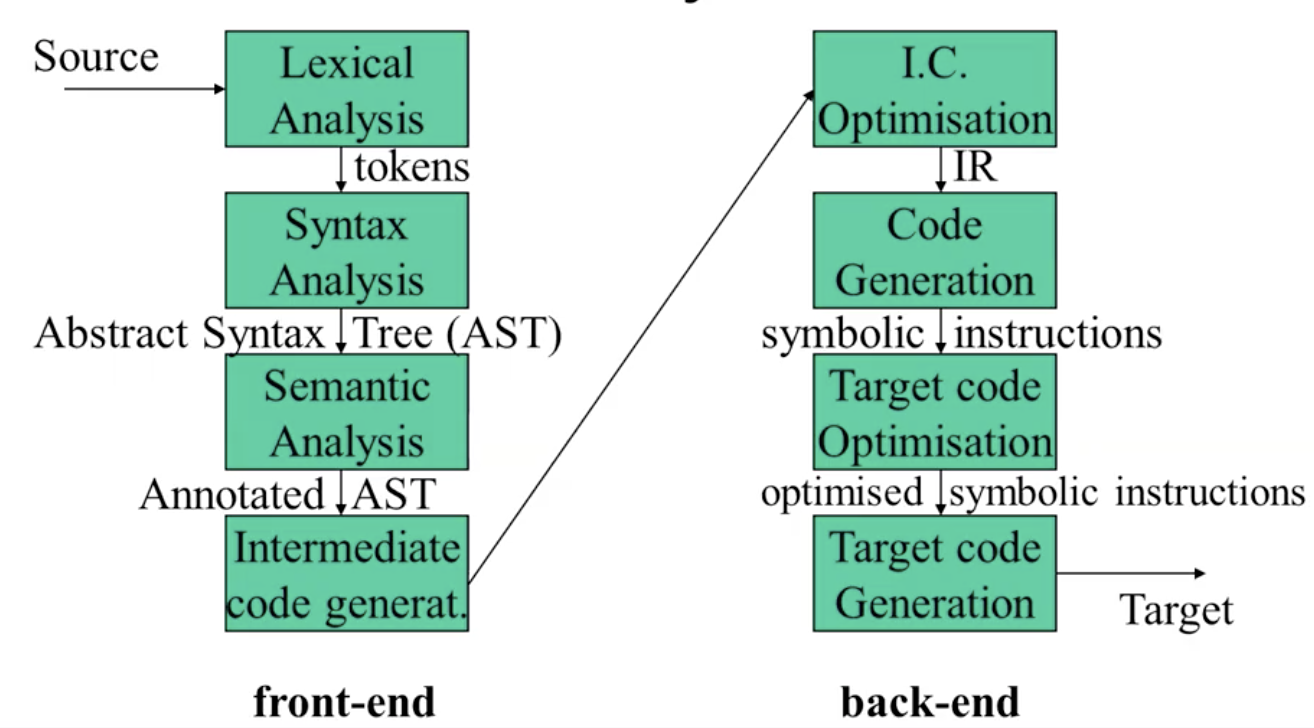
进一步地, 编译器内部又被划分为 前端 (Front-End) 以及 后端 (Back-End) 两个部分, 前端 输入源代码, 输出中间表示, 而后端以 中间表示作为输入, 输出目标代码.
前端 负责对源代码进行 分析, 源代码的合法性和可能存在的错误需要在这一阶段中被识别并反馈; 同时, 前端需要 “理解” 并收集源代码蕴含的语义, 并由此生成代码的 中间表示.
后端 负责对目标代码的 合成: 在这一阶段中, 后端将对中间表示中每一行指令和运算选择合适的指令, 并由此将中间表示翻译为目标语言.
需要注意, 前端涉及的大部分操作都可以被 自动化, 因此对常见的编译器而言执行前端操作的时间复杂度为 $O(n)$ 级别, 而后端所需要处理的问题则为 NP-Complete (要想确保完全解决这类问题需要至少指数级别的时间复杂度) 的.
编译器中 前后端分离 的架构便于编译器的 模块化, 它允许我们将 能够生成或处理相同类型的中间表示的, 针对不同语言的前后端进行 拼接, 从而构造出可以编译不同语言, 适配不同平台的编译器.
前端结构
我们下面讨论编译器前端的基本结构.
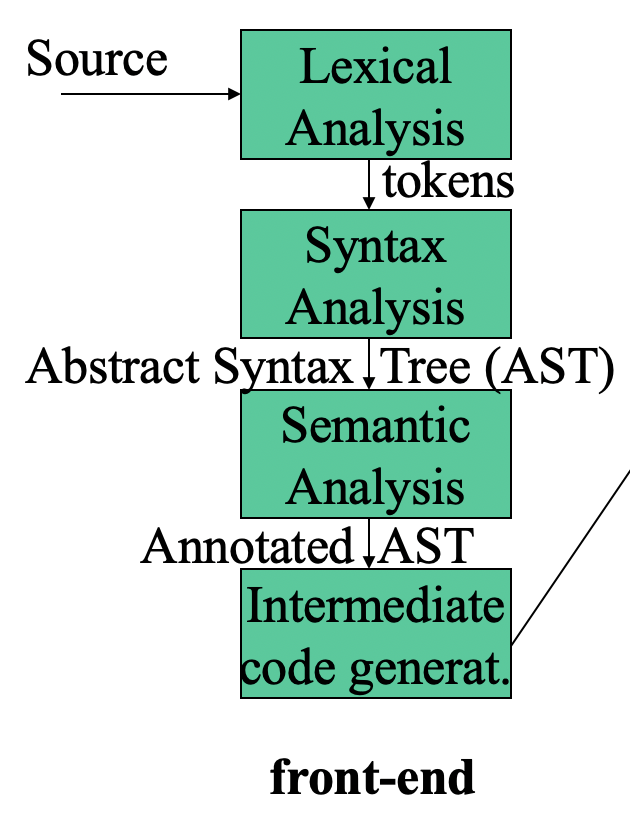
编译器前端一般由 词法分析 (Lexical Analysis), 语法分析 (Syntax Analysis), 语义分析 (Semantic Analysis) 和 中间表示生成 (Intemediate Code Generation) 四个部分组成.
首先考虑 词法分析 (Lexical Analysis, Scanning). 在这一步中, 编译器前端需要:
-
扫描, 读入源代码的字符, 并将其 分组为词汇 形成有意义的 词素序列 (
Lexeme). -
生成词汇, 并分析不同词汇的 类型, 生成将要传递到下一步中进行语法分析的 词法单元 (
\[\text{<type, lexeme>}\]Token). 其形式一般为或
\[\text{<token\_class, attribute>}\] - 此外, 在生成词法单元时, 词法分析器还需要维护 符号表 (
Symbol Table). - 在词法分析中, 空格, 注释等和程序逻辑无关的内容都会被过滤.
其次考虑 语法分析 (Syntax Analysis, Parsing).
在语法分析这一步中, 第一步中生成的各词法单元将被 解析, 从而生成 树状的中间表示, 常用的就是 语法树. 树状的语法结构将被用于编译器的后续步骤来分析源程序并生成目标程序.
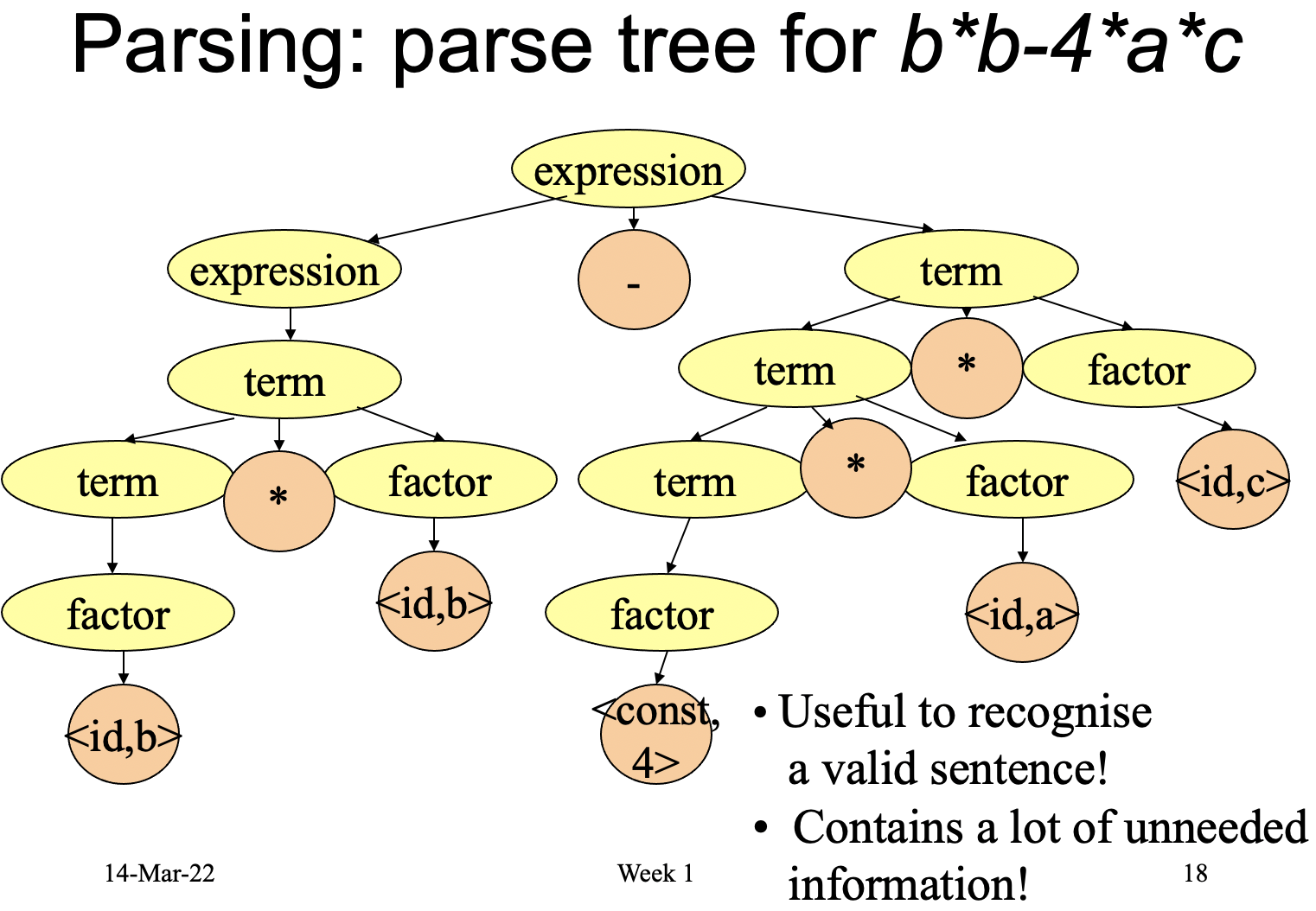
一般地, 生成树还会被进一步通过删去多余的信息被简化为 抽象语法树 (Abstract Syntax Tree, AST):
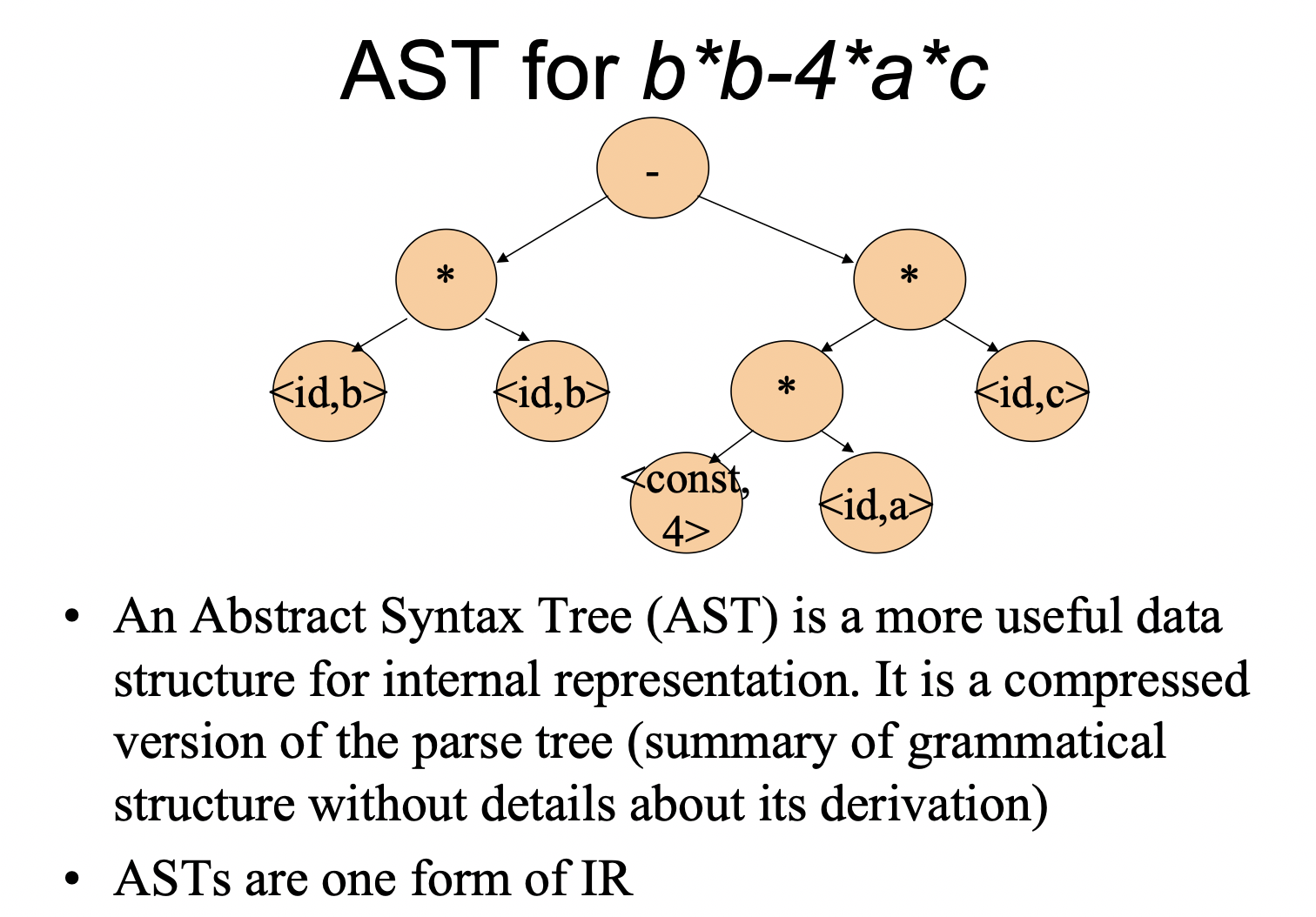
然后考虑 语义分析 (Semantic Analysis, Context Handling):
语义分析由 语义分析器 完成, 负责收集语义信息, 检查语义错误, 如类型检查, 检测变量是否被合法地声明, 进行变量与函数的命名检查等. 它还将使用语法树和符号表中的信息检查源程序是否和源语言定义的语义一致.
此外, 语义分析器也会收集 类型信息, 并将这些信息放在语法树或符号表中.
语义分析器最重要的功能是 类型检查: 检测每个运算符 (Operator) 是否具有 匹配的运算分量, 若目标语言要求某个数组的下标必须是整数, 则若用浮点数作为下标的时候编译器就会将这种操作认定为类型错误.
最后考虑 中间表示生成 (Intemediate Code Generation).
编译器会在完成源代码的词法分析, 语法分析和语义分析后生成一个 明确的, 类机器语言的中间表示. 本质上, 中间表示是一种对源代码的抽象, 合格的中间表示必须是便于生成且便于翻译的, 常用的中间表示形式是 三地址指令 (Three-Address Instruction).
后端结构
继续讨论编译器的后端结构.
编译器后端一般由 中间表示优化 (Intermediate Code Optimisation), 代码生成 (Code Generation), 目标代码优化 (Target Code Optimisation) 和 目标代码生成 (Target Code Generation) 构成.
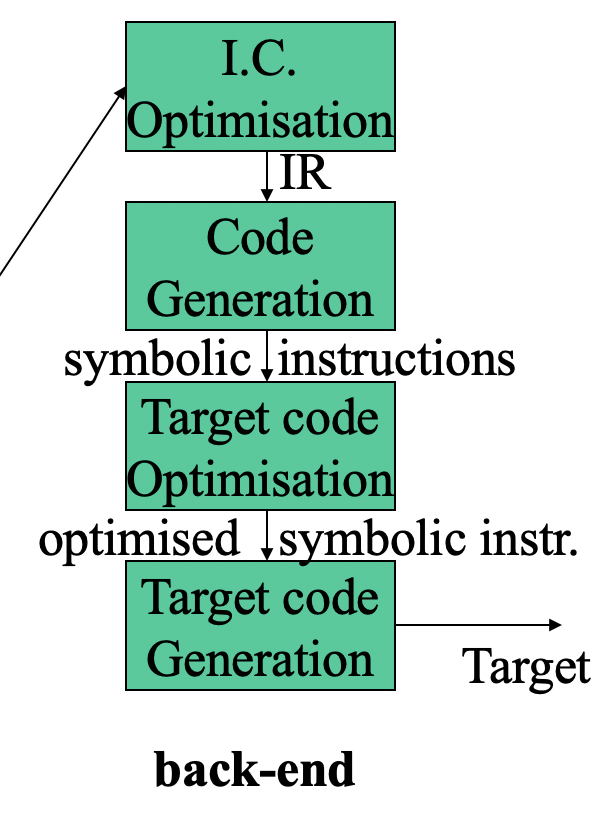
先讨论 中间代码优化. 在这一步中, 编译器后端会尝试基于预先给定的目标 (如生成能耗更低/更短/更快的代码) 对传入的中间代码进行优化.
而在后续的步骤中, 需要以经过优化的中间代码作为输入, 并将其映射为目标语言. 若目标语言是机器语言, 还需要在这一步中 选择合适的机器指令, 为每个变量分配寄存器或指定内存位置.

相关题目解析



2. 词法分析 Lexical Analysis
在本节中, 我们讨论词法分析步骤中的基本原理.
回顾定义, 词法分析是读入程序源码并将其转换为一系列词素 (Token) 的过程.
为了避免人工编码复杂的词法分析器, 简化程序语言的语法定义和实现, 词法分析器对编译器而言至关重要.
为了便于后续的解释, 此处引入一系列定义:
基本定义
定义 2.1 (单词表, 字符串, 语言和语法)
- 称由一系列不同符号组成的集合为单词表.
- 称由一系列单词表中的符号组成的有序队列为字符串.
- 称由所有定义在某个单词表上的字符串组成的集合为语言.
- 称任何一种有限的, 表示语言的方式为语法.
定义 2.2 (上下文无关语法, Context-Free Grammar)
记上下文无关语法 $G$ 为四元组
\[G = (S, N, T, P):\]
- $S$: 起始符号 (
Starting Symbol)- $N$: 非终止符号 (
Non-Terminal Symbol)- $T$: 终止符号 (
Terminal Symbol)- $P$: 生成规则
因此我们也可将语言定义为由某个上下文无关语法生成的所有终止的字符串组成的集合. 如:

注:
- 一般情况下非终止符号均用大写字母表示.
- 上面的例子中使用的是
LeftMost Derivation: 基于规则从左到右逐步构建字符串.
上下文无关语法对于词法分析至关重要. 使用恰当的表示方法, 我们即可利用上下文无关语法高度的结构性和过程性对程序语言的语法进行编码. 下面简介其中一种恰当的表示法: 正则表达式.
正则表达式
正则表达式 (Regular Expression) 用于表示正则语言, 我们可以使用正则表达式表示无穷种字符串.
正则表达式的基本语法:

需要注意, 正则表达式的基础语法恰为前三条, Shorthands 实为对前三条规则的简化封装, 类似语法糖.
虽然 正则表达式无法用于表示所有语言, 但它足够解决绝大多数的问题. 下面给出正则表达式表示整数, 浮点型和变量名的例子. 在 Python 表达式的例子中, 我们使用正则表达式分别用常规方式和科学技术法表示了浮点型数字.

如上文所述, 理论上我们完全可以将词法分析规则硬编码, 但这样做会极大降低分析器的可扩展性, 难以修改, 且工作量巨大. 正则表达式恰可以 自动化词法分析的过程, 极大地简化我们在构造词法分析器时的工作.
如下图所示, 正则表达式实际上可以被表示为状态转换图.
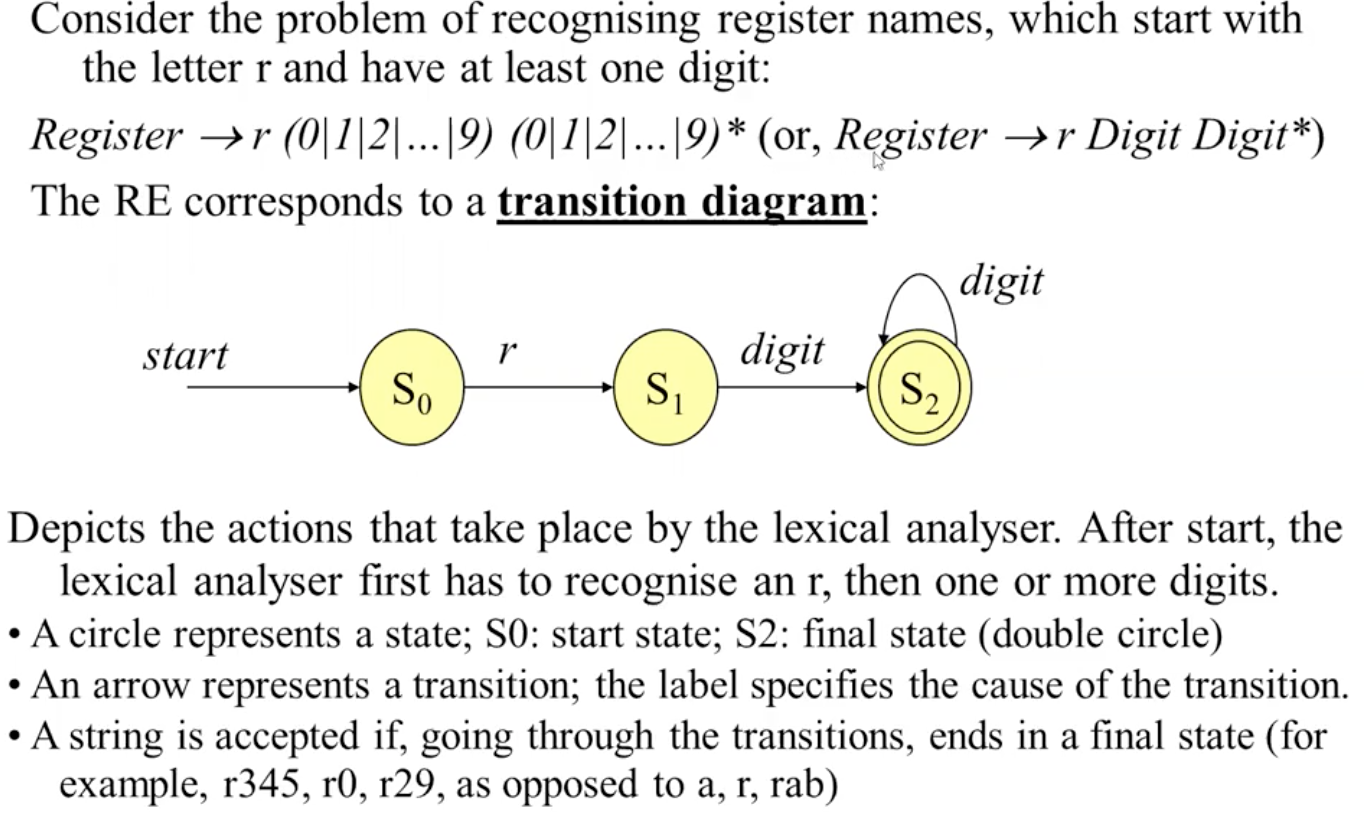
上图中的转换图可以被相应地 等价表示 为下列的转换表:

在转换表中, 第一列表示当前状态的编号, 第二列表示在当前状态下接受不同输入将会导致状态转换 (切换, 更新) 到什么新的状态上, 如在 state0 时, 若输入为 r 则所处状态将转换到 state1, 而任何其他输入都无法让当前状态转换.
进一步地, 在将正则表达式所表示的状态转换图转化为状态转换表后, 我们就可以通过在词法分析逻辑中查询和调用状态转换表, 明显地优化性能.
需要注意的是, 能够被利用的状态转换表必须是 确定性 的, 也就是在任何状态下, 给定任何输入, 其状态转换效果必须唯一. 我们下面对不同类型的状态转换图, 转换表和状态机进行讨论.
NFA, DFA 和转换与简化
在介绍各种状态机前, 我们首先明确它们在构建词法分析器的步骤中起到的作用:

我们首先使用正则表达式编码程序设计语言的语法规则, 并通过 Thompson's Construction 先将其转换为非确定性有穷状态机, 再使用 Subset Construction 将其转换为未经精简的确定性有穷状态机, 最后使用 Hopecroft's Algorithm 将其精简的方式得到可供特定的词法分析器生成工具作为输入的, 精简的确定性有穷状态机.
首先回顾确定性有穷状态机 (DFA) 和非确定性有穷状态机 (NFA) 的定义:

正则表达式到 NFA 的转换
Thompson‘s Construction 的构造规则如下:
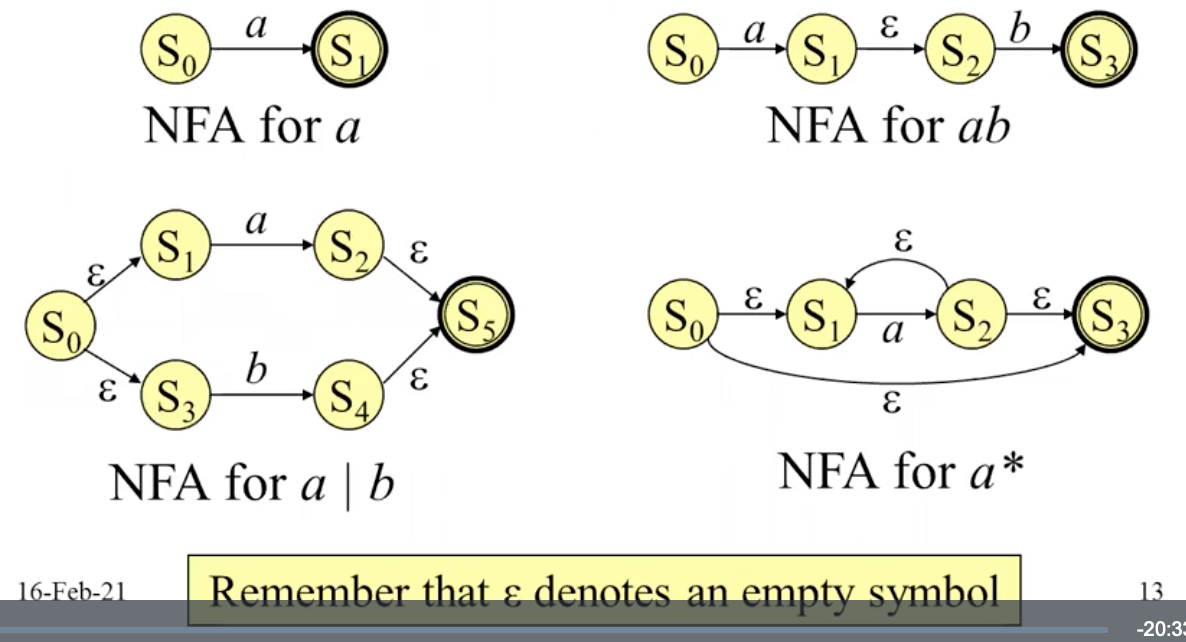
我们可以使用这些表示正则表达式基本元素的中间件构造复杂的非确定性有穷状态机, 如:
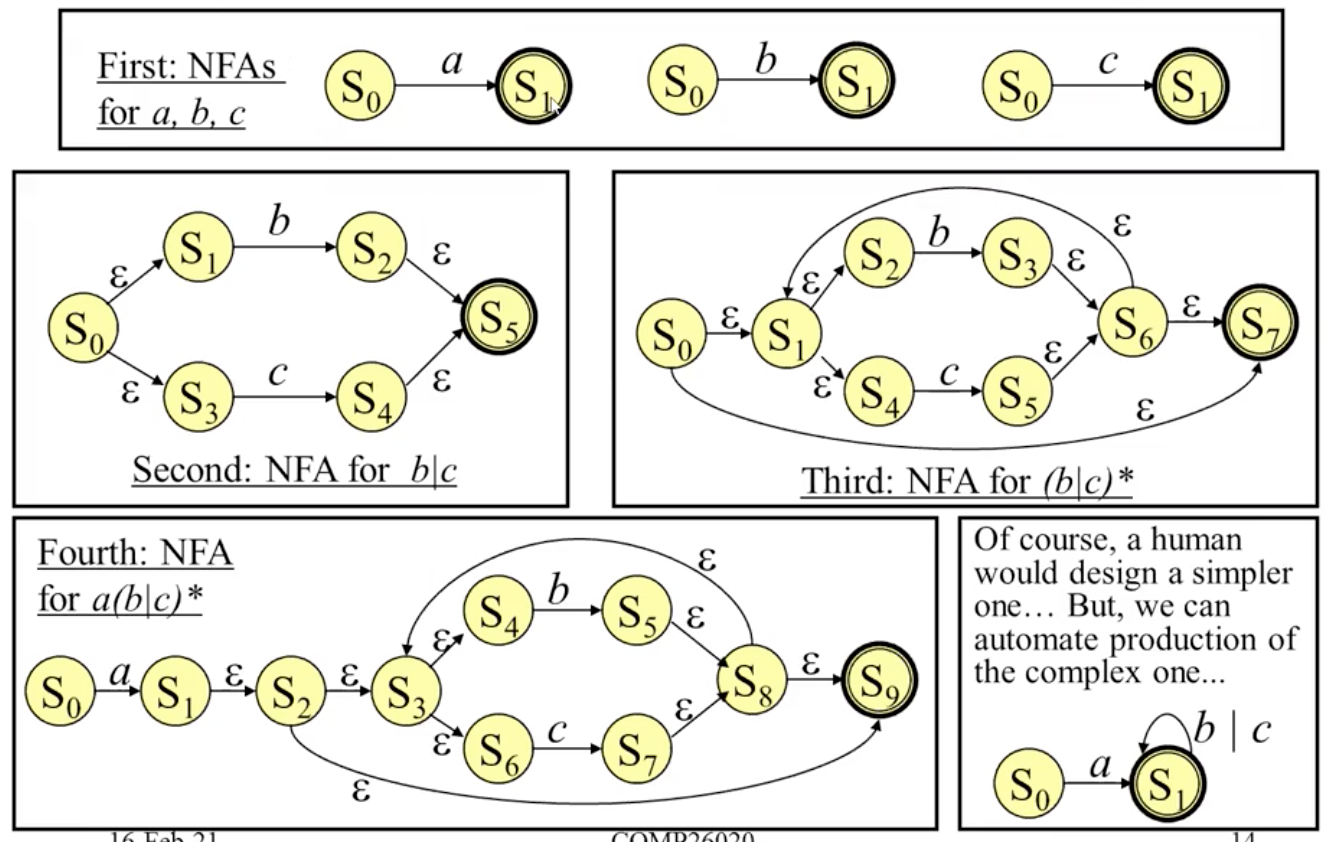
NFA 到 DFA 的转换
Subset Construction 的核心逻辑由两个操作组成:
-
move(s_i, a): 找出从状态 $s_i$ 开始, 通过输入a所可以转换到的全部新状态. -
epsilon-closure(s_i): 所有从状态 $s_i$ 开始, 通过空输入 $\epsilon$ 所可以 直接或间接 转换到的状态.
注意: 对 epsilon-closure 而言, 若考虑某个元素 $s$ 的闭包, 则闭包内包含的是 该元素本身 以及 所有通过 $\epsilon$ 转换可以得到的其他元素.
用于将 NFA 转换到 DFA 的 Subset Construction 的基本逻辑是:
- 从
NFA的 初始状态节点 开始查找其epsilon-closure. - 对找到的所有
epsilon-closure, 结合它们所可以接收到的所有类型的新输入 应用move(). - 对新生成的
epsilon-closure再循环反复应用上述规则, 直到再也无法生成新的epsilon-closure为止.
此时, 所生成的所有不同的 epsilon-closure 就代表我们得到的, 等价的 DFA 的所有节点. 依据转换规则将这些新节点编号, 连接, 就得到了和原来的 NFA 所等价的 DFA.
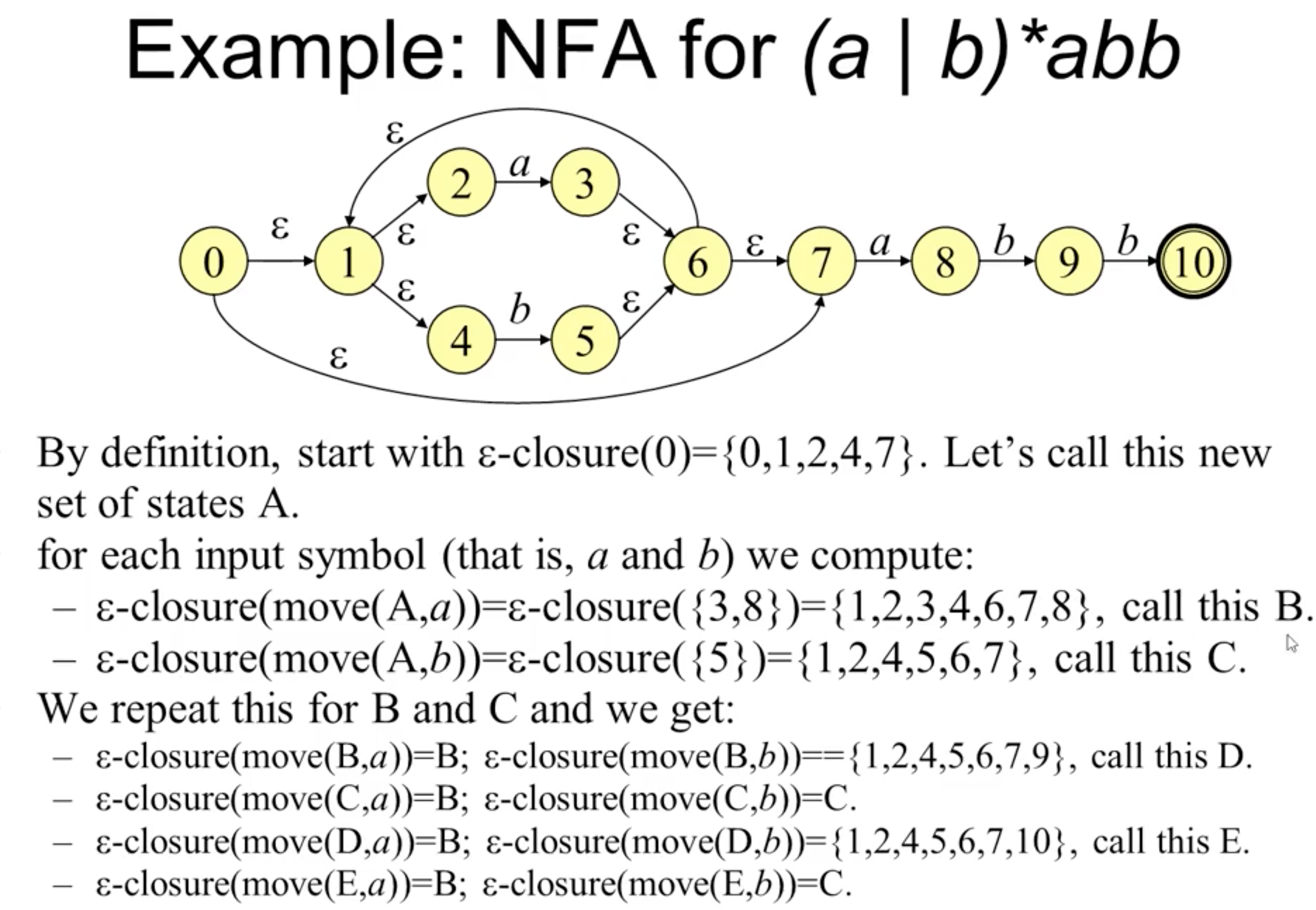
在上面的例子中, 我们从 NFA 的初始状态节点 $0$ 开始应用 epsilon-closure, 一步步扩展最终得到了五个不同的闭包. 上述 NFA 即被相应地转换为:
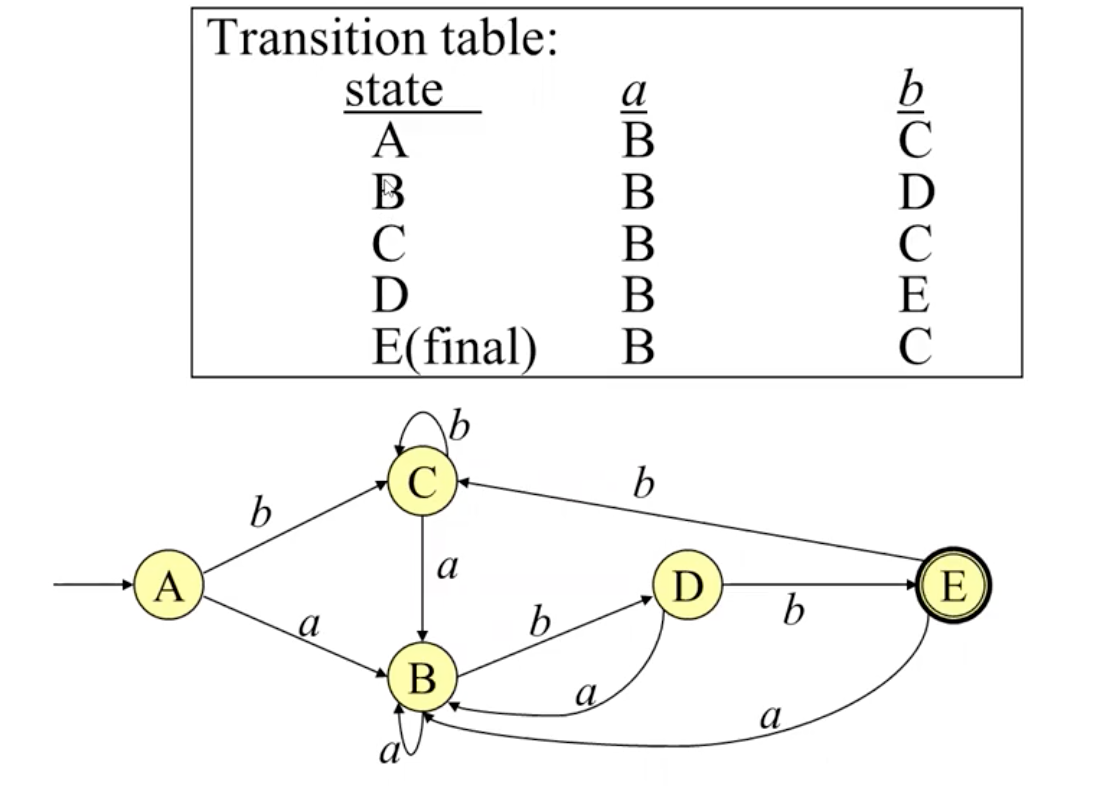
注意通过 Subset Construction 得到的 DFA 存在大量冗余节点. 下面使用 Hopecroft's Algorithm 将其简化.
DFA 的精简
在对 DFA 进行精简时, 我们将合并全部状态转换规则相同的节点, 检查冗余节点的方式为 Hopecroft's Algorithm 的基本思想:
首先将输入 DFA 的全部节点分为两个部分: 终止节点, 和非终止节点.
其次, 根据不同输入分别判断: 非终止节点中是否有某个或某些节点在输入某些符号时状态转换的规则和其他的不一致. 如果对于任何一种输入出现了这种情况有的话, 将其聚类并拆分.
对拆分后的节点集继续进行相同的检测, 直到无法再拆为止. 此时我们得到的一系列拆分后的节点集合就表明了原 DFA 中哪些节点是互相等价, 可以合并的. 如:
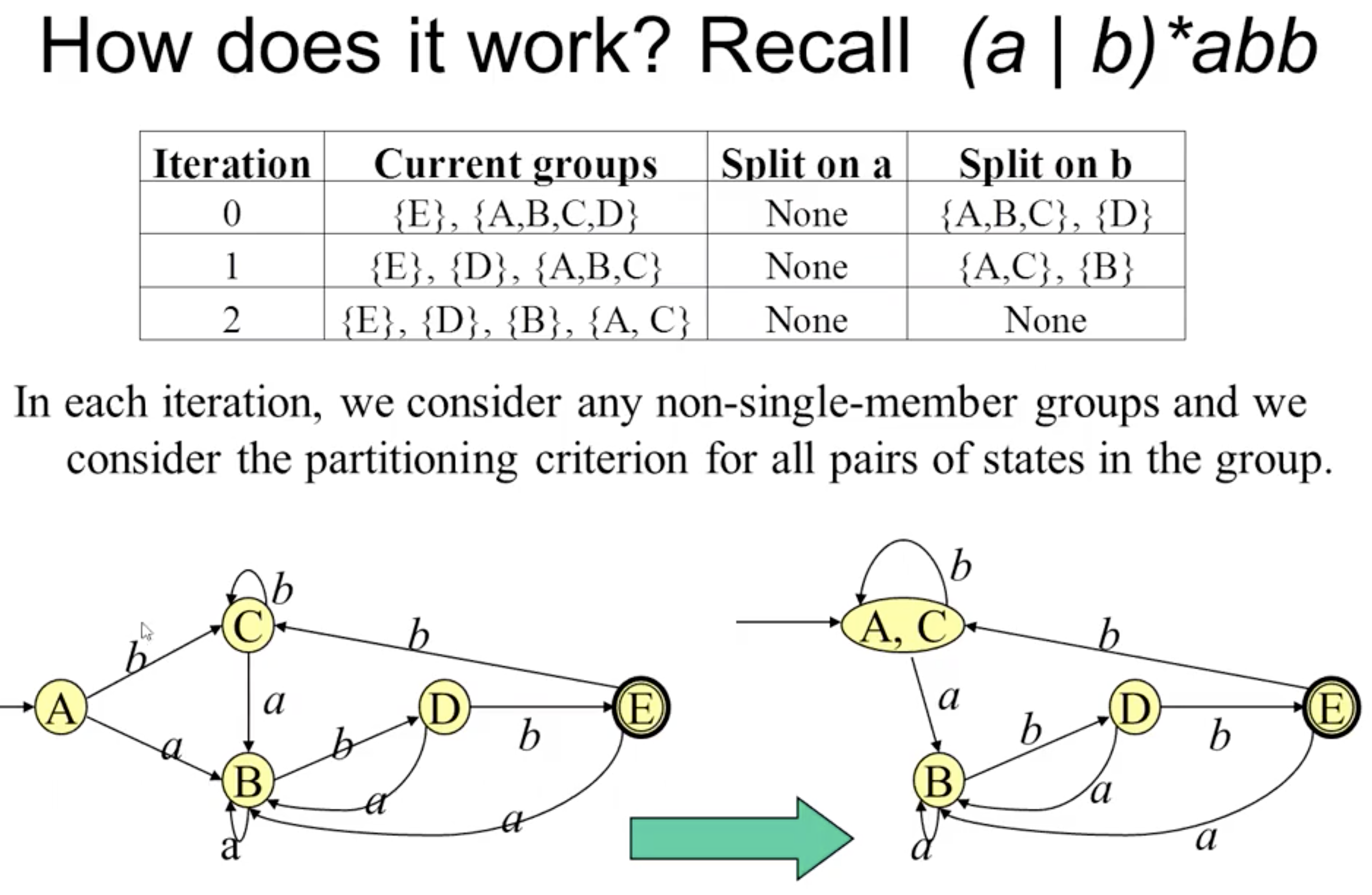
以及
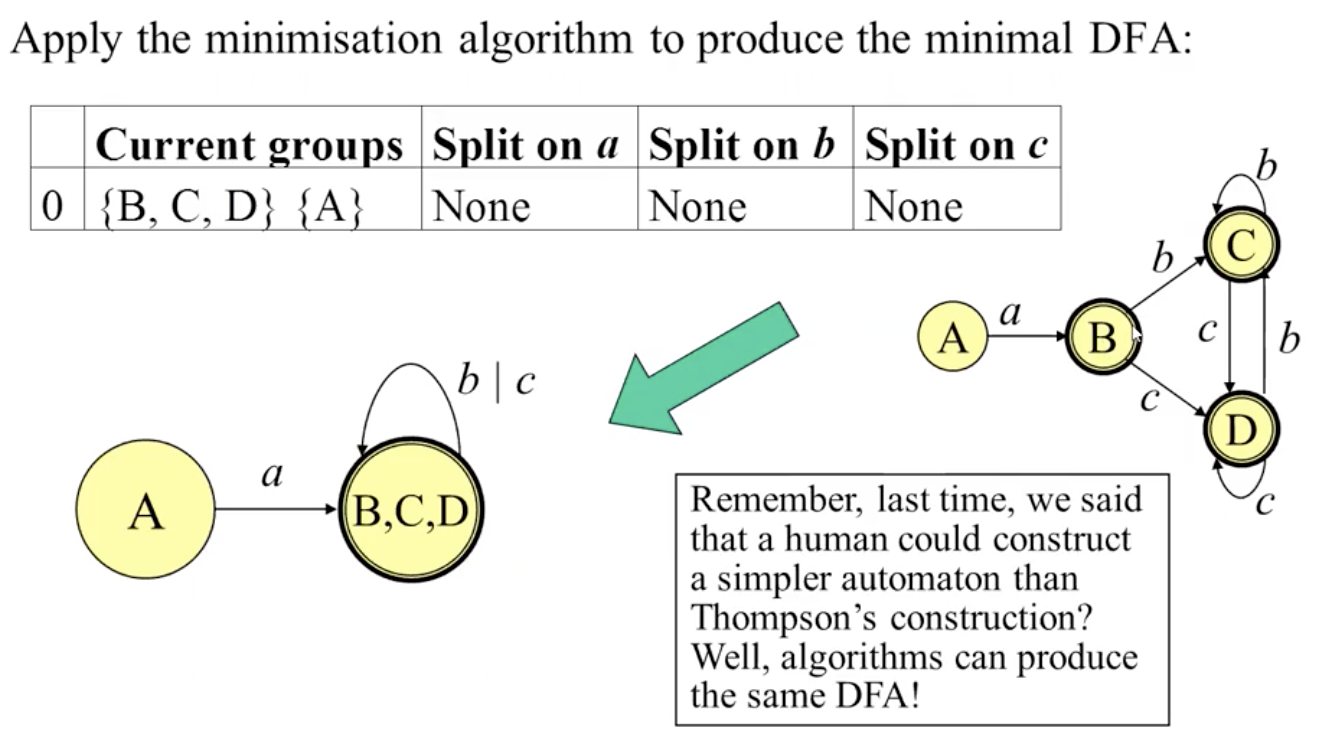
构造高效的词法分析器
在上面一小节中我们已经解释了如何从正则表达式通过数种中间形态转换到精简的确定性有穷状态机的过程. 而在将确定性有穷状态机转换成完全等价的状态转换表后, 它就可以被词法分析器调用以相对高效地完成词法分析任务.
然而调用状态转换表仍然相对低效, 且会产生可观的内存开销. 因此, 契合实际的解决方案是: 将状态转换表编码的转换规则使用工具直接 自动化地集成 到词法分析器中.

在业界中, 常用的转换工具为 Flex:

它可以直接接受正则表达式为输入.
总结
词法分析器将由一系列符号组成的源码经过分析和转换, 变为一系列词素. 这一过程是完全自动化的, 遵循 “正则表达式 - 非确定性有穷状态机 - 确定性有穷状态机” 的流程. 由于正则表达式具有表达多种复杂模式的强大功能, 它常被用于自动化词法分析的流程.
相关题目解析

3. 语法分析 Syntax Analysis
在上面一节中, 我们已经介绍了词法分析的作用, 原理, 操作方法, 涉及的主要定理/算法与其他细节. 下面我们讨论完成词法分析后的下一步骤: 用于 生成构造出词法分析给出的一系列词素的流程 的 语法分析.

我们首先明确语法分析的对象. 乔姆斯基的语法层级将语言大致按照逻辑严密性区分为了四个类别:

其中人类日常交流使用的自然语言语法位于最高 (也是逻辑性最差) 的一级, 正则语法的逻辑性最强, 而语法分析所需要处理的语言则为位于倒数第二级的 上下文无关语法.
这是由于正则语言存在两点无法避免的局限性:

正则语言无法表示存在对称性和需要计数的字符串语言, 也无法直接应用未经完备定义的非终止符号.
语法分析的目的是基于给定的语法, 分析出给定语素序列的 推导过程 (Derivation), 以及推导过程对应的 分析树 (Parse Tree).
在分析推导过程时, 在每一步分析时都需要选择某个非终止符号并用合适的语法生成规则取代它, 而在每一步中选择不同的符号都会导致最后得出不同的生成规则.
在编译器构造问题中, 我们主要关注的推导过程类型分为两种, 左起推导和右起推导:

而分析树则是对推导过程的可视化.

语法分析需要避免歧义性, 否则分析过程中会涉及相当数量的错误选择和回溯. 回顾定义, 我们知道, 歧义性语言 就是那些可以使用不止一种方式生成某些文字, 也就是分析过程会生成不止一种生成树的语言.

为了避免歧义性, 我们需要确保被分析语言的语法是不具歧义的. 解决这一问题的方法是 重写语法规则.
下面先介绍两种常用的语法分析方法: 自顶向下分析 和 自底向上分析, 并分别再讨论不同语法分析方法中解除歧义性的方法.

需要注意, 编译器常使用自底向上分析法.
自顶向下分析
自顶向下分析从 语法规定的起始符号 开始, 从根开始 自顶向下 分析语素序列, 构造对应的语法树, 直到我们构造的推导规则完整匹配了给定的序列为止:

而有效执行自顶向下分析的前提是在每一步分析时都选择语法中正确 (合适) 的生成规则, 否则分析器就需要回溯, 造成时间和资源的浪费. 举例而言, 基于下图所示的语法处理给定的字符串, 就有可能得到两种完全不同的生成规则:
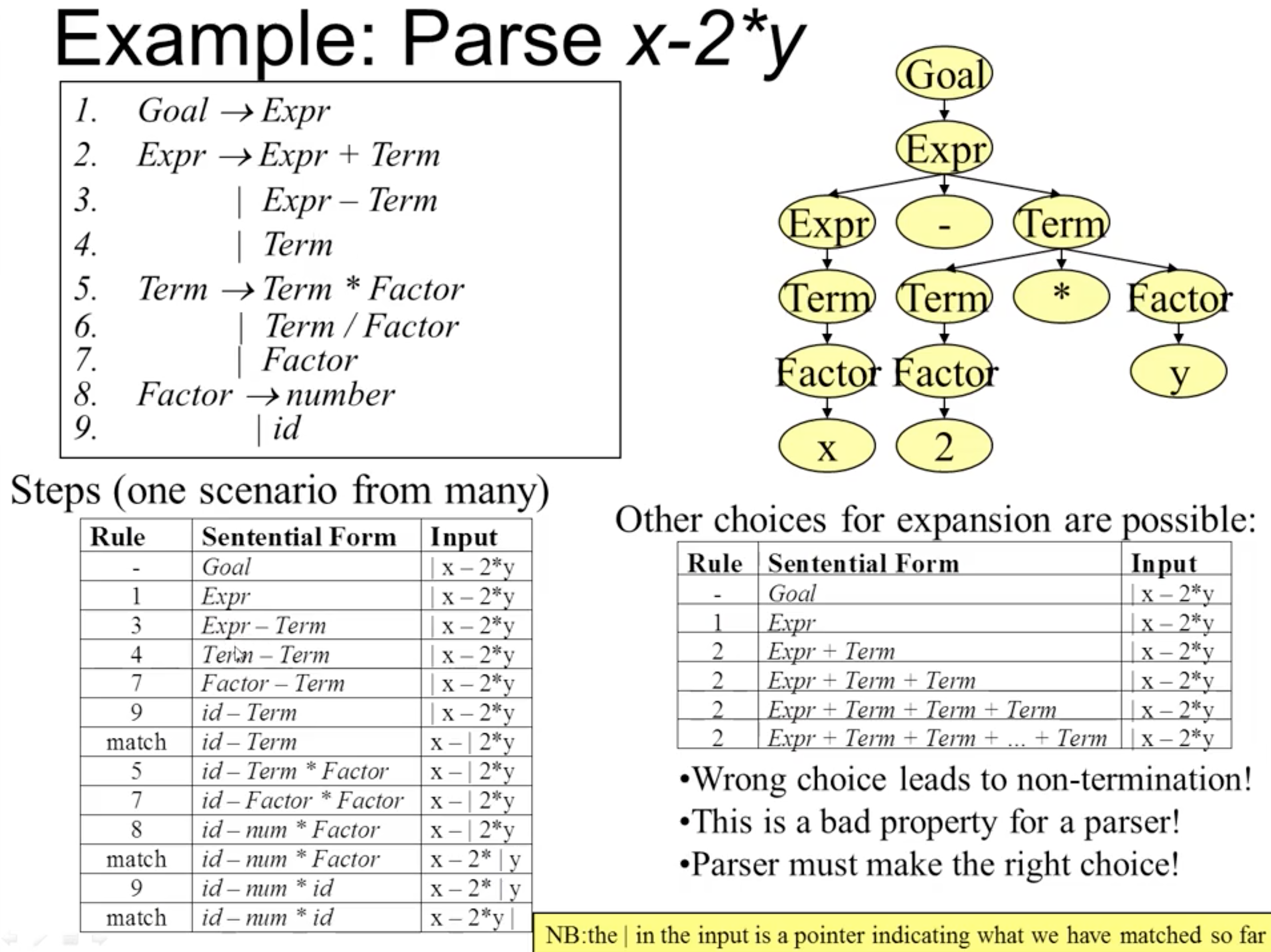
而由于自顶向下分析的特征, 我们需要确保对应的语法 不为左递归 (left-Recursive) 的:

而通过重写消除左递归, 我们就可以确保新的语法具有 LL(1) 性质:

在将语法生成规则重写确保它不为左递归的之后, 我们就可以开始考虑在语法分析时如何进行生成规则的选择. 得益于重写语法, 我们只需要在选择时从被分析的字符开始 向前看一位, 就可以从重写后的规则中找到合适的.

自底向上分析
与自顶向下分析不同, 自底向上分析生成语法树的方式是 从最底下的叶子节点开始反推, 直到反向推出根节点 Goal, 这也就是从给定的输入字符串开始, 反推到起始符号的过程.
回顾语法分析的目的是构造出一个生成序列, 使得从起始符号 $S$ 开始能够一步步构造出作为输入的被分析字符串 $\text{sentence}$:
\[S \rightarrow \delta_0 \rightarrow \delta_1 \rightarrow \cdots \rightarrow \cdots \rightarrow \delta_{n-1} \rightarrow \text{sentense}.\]要从后往前地, 基于中间字符串 $\delta_{i}$ 反向推导出 $\delta_{i-1}$, 我们需要选择 $\delta_{i}$ 中的某个字符 $x$, 利用语法中现存的分析规则
\[A\rightarrow x\]将 $x$ 替换为 $A$ 从而得到 $\delta_{i-1}$. 这一步骤也被称为 还原 (Reduction).
因此, 自底向上分析中最为重要的步骤就是在每一步中进行 合适的还原. 而寻找还原的实质是, 找到:
一个匹配生成语法中某条规则右侧结果, 而且在需要被处理的字符串中 出现 的子串. 我们称这样的子串为一个 还原柄 (Handle):

需要注意:
-
显然对于没有歧义的语法规则而言, 任何一条规则的右侧结果都 唯一对应 一个还原柄.
-
在还原柄的形式化表示中, $k$ 代表的是 子串的最右侧元素在字符串中所处的位置.

举例而言, 在上图中, 尝试匹配
a A bcde时, 对应的子串Abc在字符串中的 $k$ 就应该是 $4$.
而在通过还原得到了这些还原柄后, 我们就可以相应地构建对字符串的推导过程:

下面看一个例子:
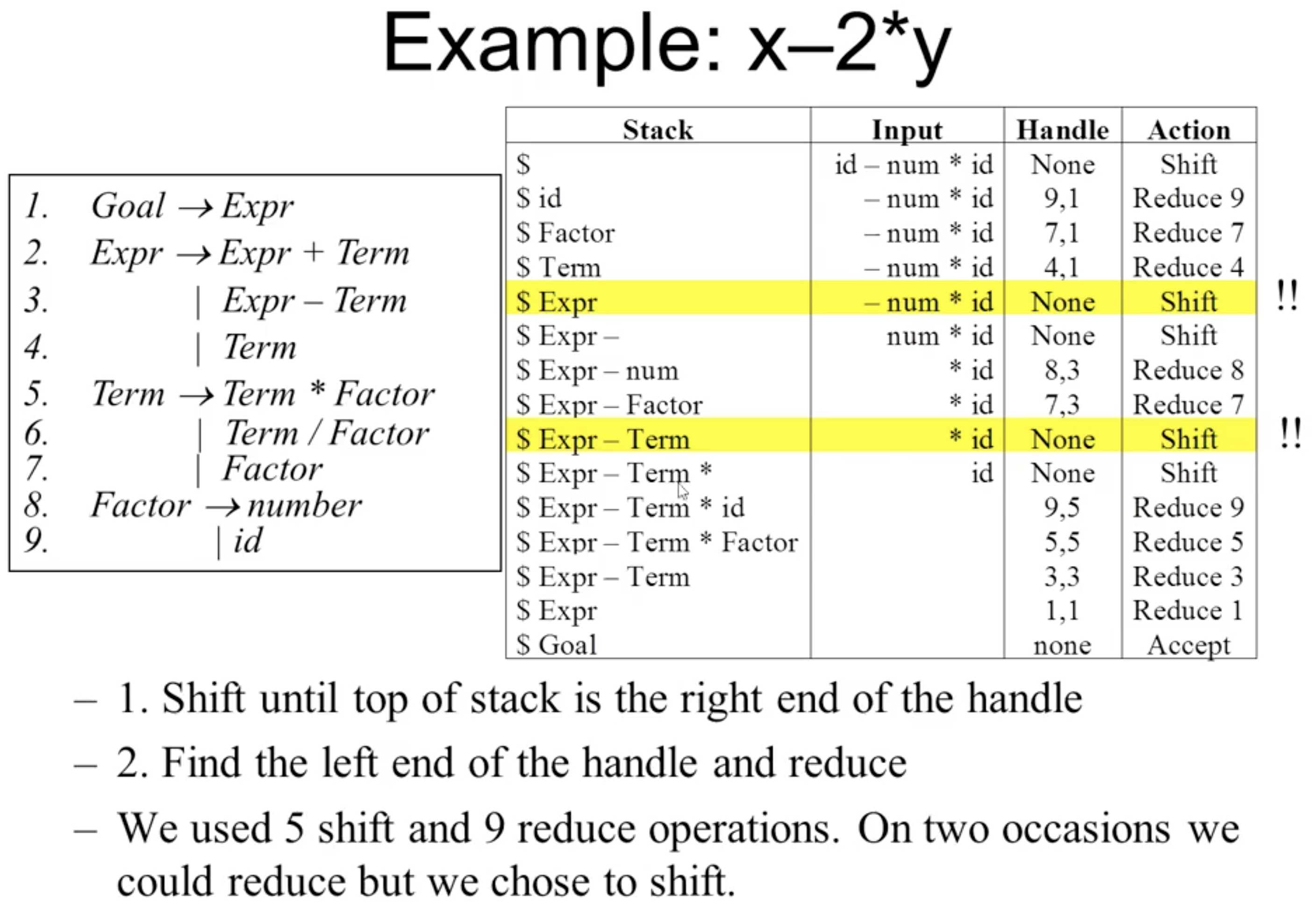
在上面的例子中, 我们手动地执行了 shift 入栈和 reduce 替换的操作, 最终得到了一个反向从字符串倒推回 Goal 的构造序列.
抽象地, 寻找还原柄和生成推导过程的逻辑可被表示为 Shift-Reduce Parser:

然而自底向上分析仍然存在两个问题需要解决. 仅从上面处理 $x-2y$ 的例子就可看出, 在黄色行处, 需要作出正确的选择: 不直接从 Expr 反向匹配到 Goal, 而是继续 shift 入栈才能得到正确的结果.
这意味着在一些情况下存在这样的问题:
-
语法分析器无法决定是执行
Shift还是执行Reduce. -
语法分析器无法决定执行哪个
Reduce规则.
前者可以通过修改语法或人为规定优先执行 Shift 解决冲突, 而后者就很难通过简单的操作缓解.
因此, 为了高效执行 自底向上分析, 需要使用 Handle-Finding Mechanism.
将 Shift-Reduce Parsing 确定化和自动化, 需要我们确保给定的上下文无关语法具备 LR(1) 性质:

注意此处在确保上下文无关语法是 LR(1) 的之后, 决定执行哪个 Reduce 规则时也只需要和自顶向下的 LL(1) 一样向前多看一位即可.
基于具备 LR(1) 性质的上下文无关语法下的, 自底向上的语法分析称为 LR Parsing.
它除了和 Shift-Reduce Parser 一样需要逐个从左向右, 自 Input Buffer 读入语素 (Token) 外, 还需要在入栈的每个符号后加入表示状态的额外信息.

它需要使用两个额外的信息表:

ACTION 和 GOTO 信息表包含了满足 LR(1) 条件的, 上下文无关语法的语法规则, 并且可以决定在什么情况下执行什么样的 Shift-Reduce 操作. 注意 ACTION 表的列数恰为终止符号的数量, GOTO 表的列数为非终止符号的数量, ACTION-GOTO 联表的列数为二者列数之和 + 1, 因为还需要额外一列存储状态信息.
自此, 我们可以利用 LR-Parsing 自动化地执行语法分析.
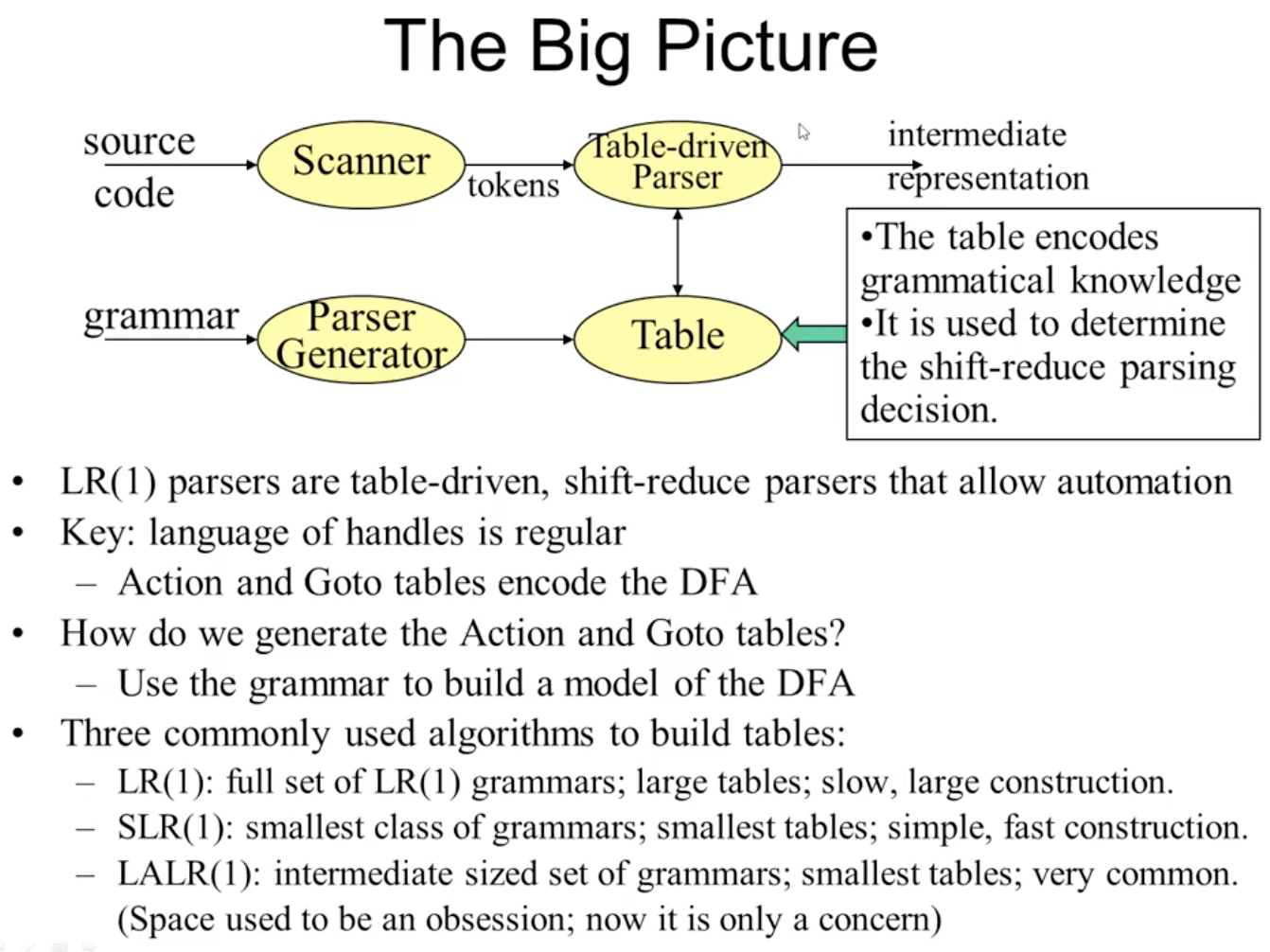
下面使用自测题中较为复杂的一道 LR(1) 查表题介绍如何解决这一类的题目:
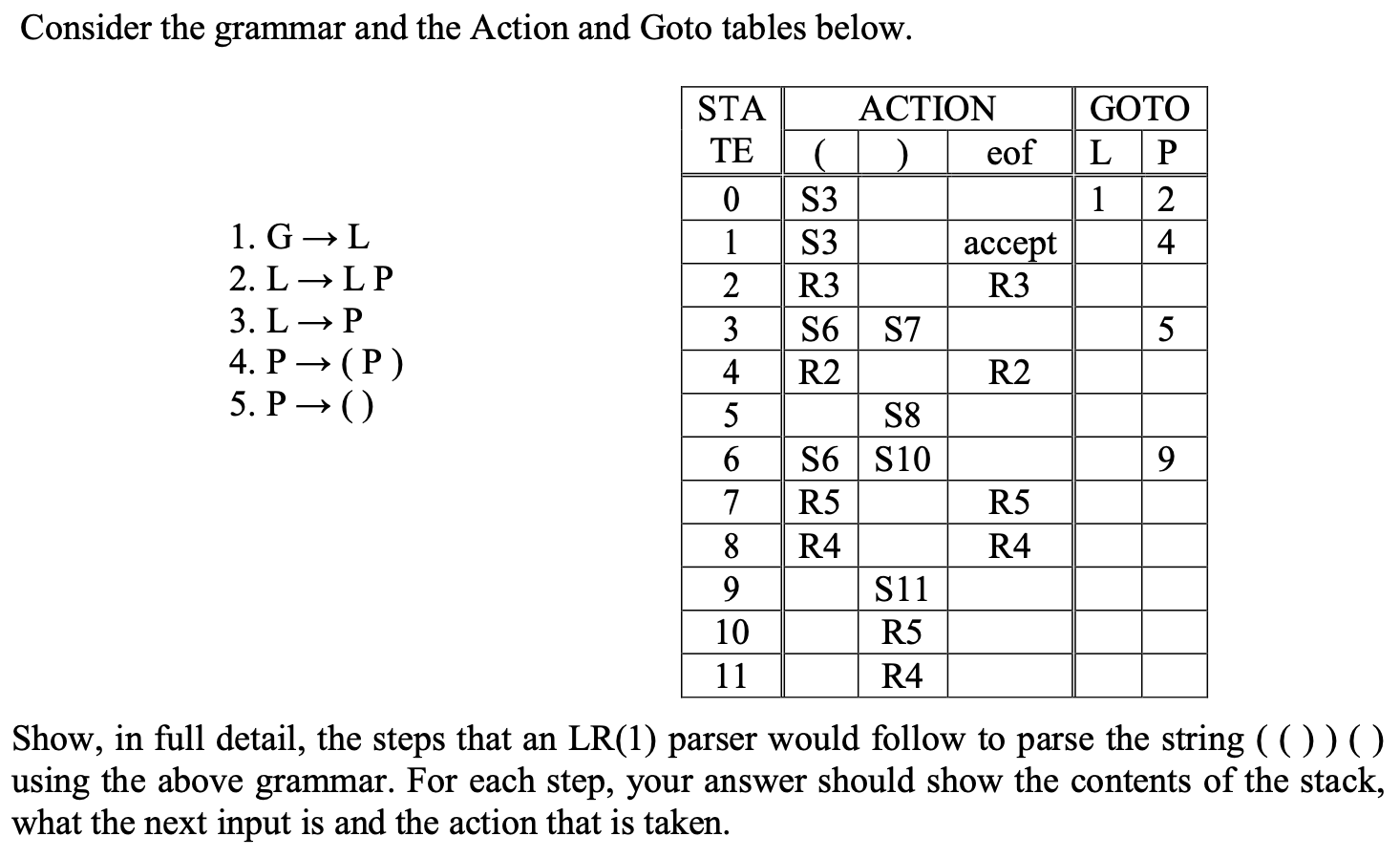
给定字符串 (())(), 转换语法和对应的 ACTION-GOTO 联表, 要求 LR(1) Parser 基于给定信息生成的字符串构造顺序.
求解这类题目时首先在草稿上画出三列联表: Stack, Input, Action, 初始状态下栈内只有一个表示栈头的元素 $, 以及初始状态 0, Input 行恰为给定字符串, Action 栏为空.
然后将 Input 中字符串的 左边第一个元素 视为状态 $0$ 时的输入, 对应查表得到, 在状态 $0$ 下输入为 $($ 时需要执行的操作为 S3, 也就是: 先 Shift, 然后通过给推入栈的新元素右侧补上 $3$ 的方式表明状态转换到了 $3$.
随后对应更新三列联表, 开始考虑 ())(). 由于此时处于状态 $3$, 输入为 $($, 查表可知需执行 $S6$, 也就是 Shift + 通过在入栈的新元素右侧记录$6$ 表示转换状态到 $6$.
然后考虑 ))(). 查表知状态 $6$ 下输入为 $)$, 需执行 S10: 入栈, 记录新元素对应状态为 $10$, 状态转移到 $10$.
随后考虑状态 $10$ 下输入 $)()$: 对应查表知需执行操作 $R5$ (Replacement Rule 5): 也就是执行替换规则 $5$. 注意在该类情况下的状态转换问题:
根据提示检查替换规则 $5$, 知需要反向将 () 替换为 P. 此时将 Stack 中的 (6)10连同字符 (括号) 后对应的状态标记 $6$ 和 $10$ 一起替换. 替换后此时 Stack 中只有 $0(3, 意味着状态转换到了 $3$.
再查表 GOTO, 知状态 $3$ 下输入为 $P$, 状态需要对应转换到 $5$, 因此 $P$ 的状态标记就是 $5$, 此时栈内元素更新为 $0(3P5.
以此类推可得:
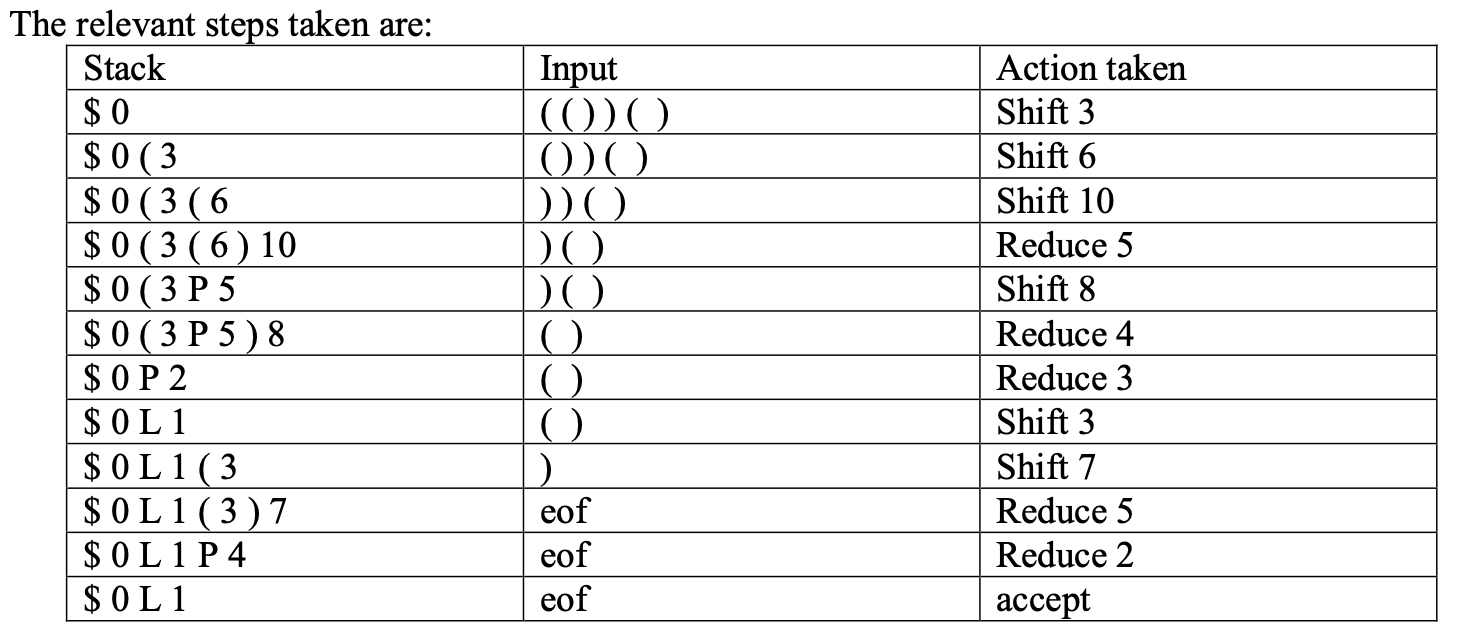
注意推导过程必须直到查表对应 Action 为 accept 方能结束.
最后我们总结如下:

相关题目解析



4. 编译器中端 (Middle-End)
在上面一节中我们已知, 通过词法分析和语法分析, 编译器可以确定输入的源码是指定程序设计语言的一段合法的代码, 也就是说如果将输入的源码视为一段字符串, 则可知:
- 输入源码中语素的顺序满足语法规定, 是指定语言的合法句子.
- 并且通过语法分析, 可以得到基于语言的语法规则生成这个句子的流程.
一般地, 语法分析的产物都是一棵 分析树 (Parse Tree), 以图形化的方式表示了如何从给定语言的起始符号开始使用不同生成规则构造出作为输入的句子 (字符串/源码) 的过程.
因此, 分析树可以作为编译器生成 和源代码完全等价, 但相对更为高效 的 中间表示 的基础. 需要注意的是, 在完成语法分析后, 我们并未完全完成对代码中潜在的其他错误, 如变量类型错误, 变量声明和引用错误等 语法分析器无法检测出 的 非语法错误, 因此在生成中间表示之前还需要执行 非语法错误检查.
非语法错误检查

在上面的例子中, 虽然给定的程序代码不存在任何语法错误, 但我们可以明确看出变量声明存在错误, 函数调用中变量多于函数声明时指定的数目, 参数化输出中给定参数类型不匹配等 非语法问题. 这些非语法问题常常是 上下文相关 的, 即单独拎出一行来分析语法错误不存在任何问题, 但放在全文中则会将问题暴露. 由于上下文无关语法无法解决和处理这类问题, 我们需要提出针对性的策略.
我们可以引入 类型系统 检测源代码中变量类型不匹配的问题.
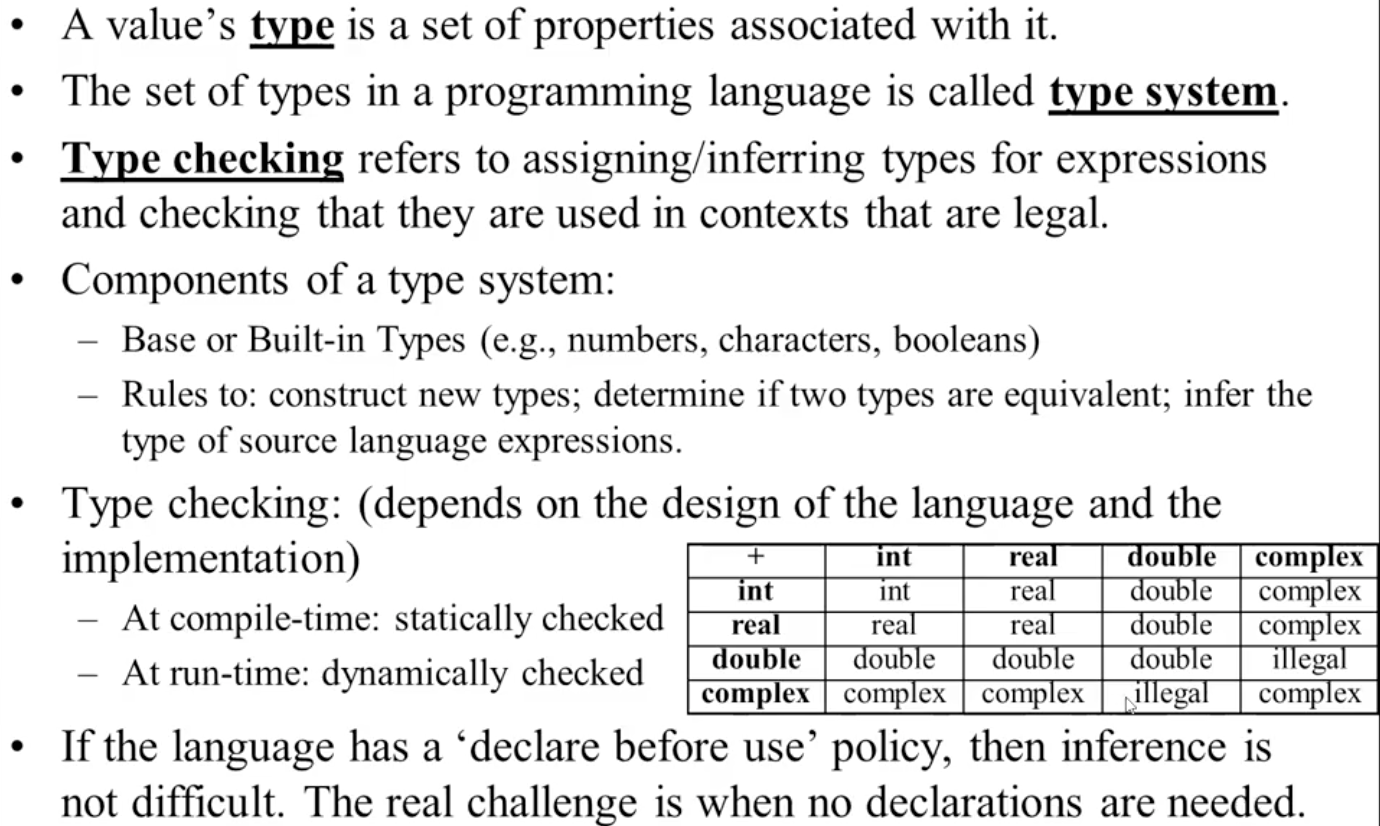
相似地, 其他类型的上下文无关语法问题也需要有对应的解决方案. 我们可以通过定义上下文相关语法将检测形式化, 但这极其困难, 且在处理一些特殊情形 (如检查变量是否在使用前声明) 时会导致需要匹配的规则数量过大以至于无法完成检测.
更为实际的做法是: 使用 ad hoc techniques, 结合某个 符号表 进行对应的检测.
符号表就是存储 词法分析/语法分析/代码错误检查时所需 的 全体事实 的数据结构, 它在词法分析时生成, 并在后续的剩余编译过程中持续被频繁调用. 通过查询和更新符号表, 编译器就可完成诸如 “变量是否都在使用之前提前声明”, 以及 “数值运算和逻辑运算涉及变量的类型是否匹配” 一类的困难问题. 而符号表中可能存储的信息类型同样是非常复杂的, 以至于实际上编译器可能需要同时维护多个符号表:

符号表可以使用线性列表, 二叉树和哈希表实现, 契合实际的实现方式是哈希表.

而哈希表的相关知识在上学期的数据结构与算法课程中已经详细介绍过, 此处不再赘述.
此外, 在非语法错误检查中还会涉及诸如哈希表中哈希函数的选择, 变量命名域等复杂问题, 这些问题不属于本课程的介绍重点, 因此不再赘述.

中间表示生成
我们下面讨论实际的中间表示生成步骤. 合适的中间表示应该满足下列的要求:

中间表示的类型包含:
-
图形 (结构可视化) 式, 一般形如树, 结构贴近源码但可能具有大量的边和节点, 导致其极其复杂.
-
线性式, 一般为伪代码的形式, 更贴近目标代码.
-
混合式, 结合了图形式和线性式的特征.
下面分别介绍一种图形式和线性式的代表:
抽象语法树 (Abstract Syntax Tree, AST)
抽象语法树基于分析树 (Parse Tree):

三地址码 (Three-Address Code)

此外, 一些辅助信息也会作为中间表示的一部分:

最后介绍一些常用的代码优化方法:


以及另一种优化循环的方法:

注意 Loop Unrolling 的目的是减少执行循环体的次数, 从而降低在执行循环条件判断和循环跳转过程中的各种开销.
最后总结如下:
- 在编译器的中间表示生成步骤中有多种不同的中间表示类型可选, 本课程简要介绍了抽象语法树和三地址码两种.
- 在这一步中我们同样可见, 除了正确地表示源码的含义外, 检查源码中潜在的非语法错误同样是一件极其困难的任务, 现代编译器一般使用基于哈希表实现的符号表处理这一问题.
- 在本节中我们同样介绍了数种与硬件无关的中间表示代码优化方法, 但为了实现极致的优化, 实际的编译器往往还要在目标代码生成时执行更复杂的, 更底层的优化手段.
相关题目解析


5. 代码生成
代码生成属于编译器后端需要完成的任务, 它接受编译器中端生成的中间表示, 并将其经过转换和优化后, 生成最后的目标代码.
在这一过程中, 主要会涉及两个问题:
- 如何使用 模式识别 (
Pattern Matching) 选择合适的目标语言指令? - 如何基于目标硬件平台的特性进行针对性的代码优化?
而在本课程中, 我们将只关注下面的三个问题: 指令选择, 寄存器分配和指令调度.
指令选择 (Instruction Selection)
指令选择这一步中的主要任务是基于 模式识别 将中间表示和目标代码相匹配. 在这一步中, 我们不进行任何优化, 且假设寄存器的数量完全足够.
我们将在下面的讨论中使用如下图所示的, 形如 RISC 汇编语言的伪机器语言:

数值运算表达式 (Arithmetic Expressions) 的代码生成
在生成数值运算表达式的代码时, 编译器采取的遍历策略是 类似遍历树一样的后序遍历.

而针对相关的问题, 也有对应的处理策略:

注意:
- 优先遍历左子树的原因是我们总是需要优先考虑对寄存器有更高利用需求的子树.
- 将常规乘法转换为多个 可表为$2$的幂的数和变量相乘 的形式后, 就可以使用 位运算 提升计算速度, 降低资源开销.
数组引用代码生成
程序设计语言定义数组的方式一般分为 行主导定义 (Row-Major Order) 和 列主导定义 (Column-Major Order), 我们目前所学习的绝大多数程序设计语言所使用的都是行主导定义.

在明确了数组首元素的内存地址和需要引用的数组元素坐标后, 就可以结合数组的定义方式快速地计算出需要被引用元素的内存地址:

控制语句代码生成
对于形如 if...else... 的控制语句, 在生成其对应目标代码时, 首先需要生成条件判断部分的代码, 其次分别生成对应条件分支对应的代码.

对于形如 while..., loop..., do loop... 的循环语句, 需要在循环开始前和循环结束后都生成条件判断语句对应的代码以控制循环.

同时, 也可以通过类似树遍历的方式处理复杂的布尔表达式. 注意在此处可以利用短路特性 (Short-Circuit Evaluation) 简化表达式.
程序/函数/方法代码生成
程序, 方法和函数的引入便于人类理解和编写复杂程序, 但它们对于编译器和计算机而言非但是完全不必要的, 反而会在编译过程中带来一定的困难. 由于计算机执行代码的过程实际上是顺序流式的, 因此编译器需要在编译过程中 “模拟” 出函数/方法, 如通过分支跳转等方式调用函数, 为不同的函数和方法划分单独的寄存器空间存储函数变量等.

对函数/方法的模拟的代价是较大的资源开销. 因此, 包括 Java 在内的一些语言在编译时会尽可能地通过直接将对应的函数代码段插入过程流的方式减少在实际目标代码中涉及的, 所需要模拟的方法数量.
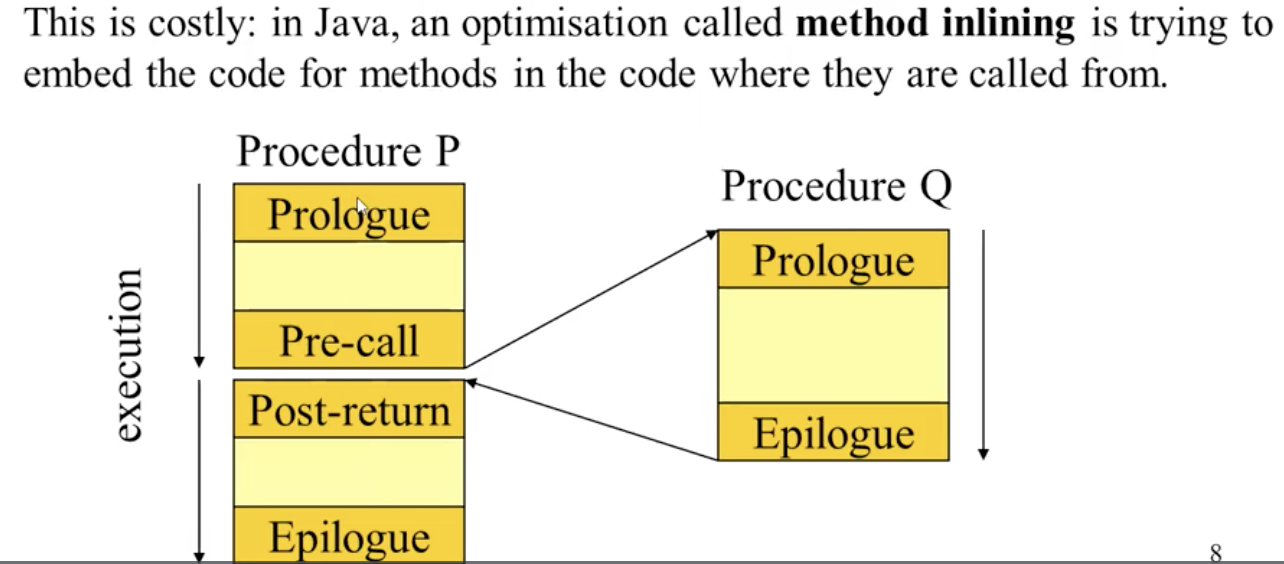
寄存器分配 (Register Allocation)
在指令选择这一步中, 我们假设可供使用的寄存器数量是无限的, 这显然不符合事实. 因此, 代码生成的下一步就是通过执行寄存器分配优化目标代码中寄存器的使用数量, 使其满足实际物理机上寄存器数量的限制.
下面首先给出一些定义:
Basic Block: 最长的, 不含任何分支跳转 (限于控制流语句和循环语句) 的代码段.- 局部寄存器分配: 在
Basic Block中执行的寄存器分配. - 全局寄存器分配: 在程序全体中执行的寄存器分配.
- 寄存器分配: 决定将什么变量/数据存储到寄存器中的过程.
- 寄存器赋值: 选择特定寄存器存储数据的过程.
现代处理器包含多种, 大量寄存器, 因此寄存器分配问题是非常复杂的. 本小节只对寄存器分配的原理和规则进行极为简单的介绍.
变量的生命概念和生命周期
引入这一概念的主要目的是解决 “在某个 Basic Block 中最多需要多少个寄存器” 的问题, 通过引入生命周期, 我们就可以计算出 “同时有多少个变量正在被程序使用” 以及 “特定的变量何时不再被使用, 可被清除” 的问题.
我们称变量的生命周期介于 变量被声明 以及 变量最后一次被调用/使用 之间, 可以表示为 Basic Block 中的一个分段 (Interval).
如果某个 Basic Block 中的任何时间段里, 活跃的变量数超过了物理寄存器上限, 就需要基于一定的规则踢掉 (Spill) 某些变量, 为其他变量创造空间.

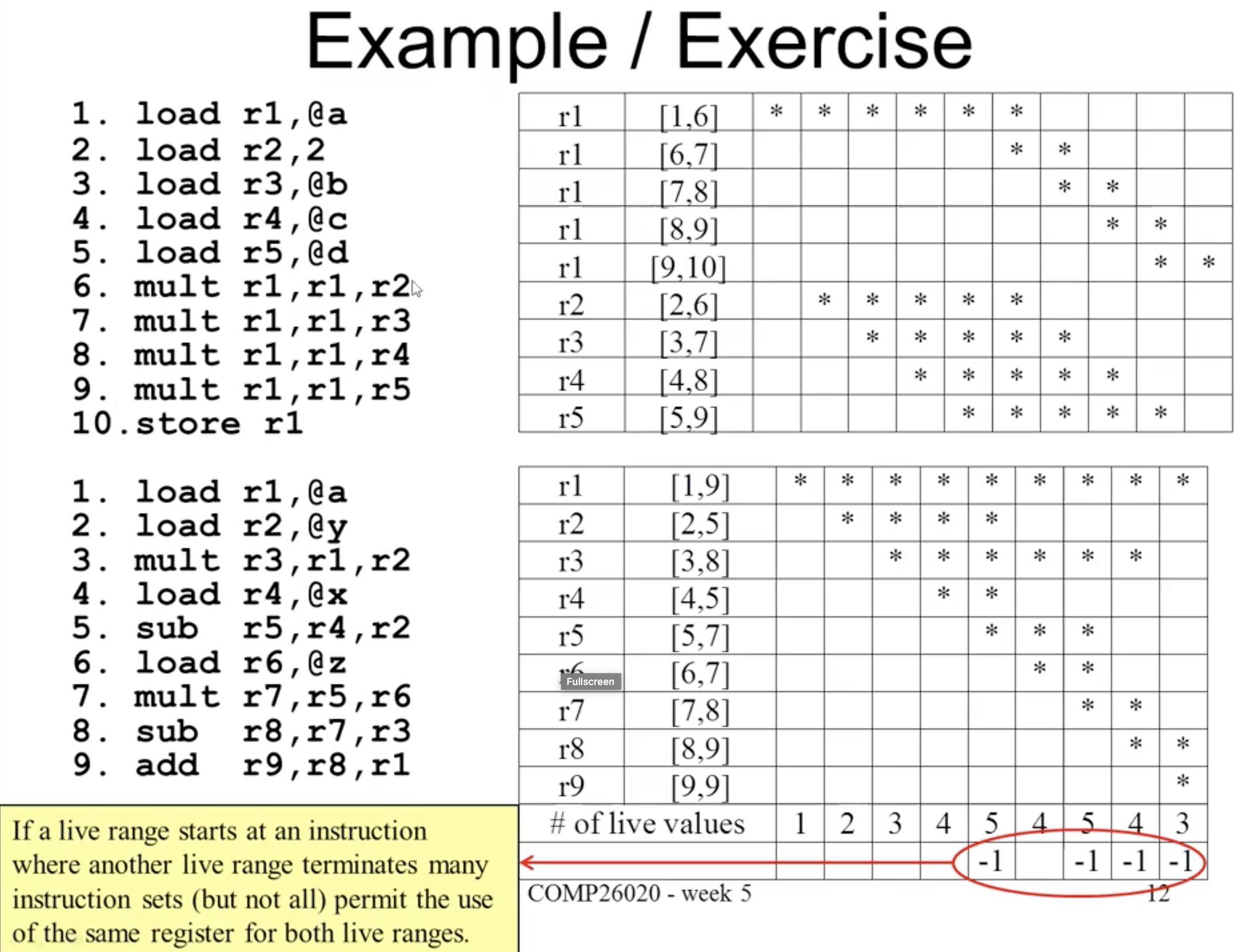
我们可以通过估计踢掉特定变量的 成本 决定在寄存器不足时需要踢掉哪个变量:

寄存器分配原则
我们着重关注局部寄存器分配问题. 局部寄存器分配问题的解决方案分为 自顶向下寄存器分配 和 自底向上寄存器分配.
自顶向下寄存器分配原则为使用最频繁的值优先保留寄存器空间, 但这可能导致在上一段代码中频繁使用, 而在下一段代码中几乎不使用的变量挤占了下一段代码的寄存器空间, 因此不切实际.
自底向上寄存器分配原则使用 “寄存器池” 的概念: 任何变量开始生命周期时都从池子里拿走一个寄存器, 而在生命周期结束时返还寄存器到池子里, 若池子里没有足够的寄存器, 就需要让 在最远的未来才会被调用的寄存器 释放值, 这也就是 Best's Algorithm.
使用图染色方法解决寄存器分配问题
我们还可以使用图染色方法解决寄存器分配问题.
其基本逻辑是: 生命周期不互相干涉 (Interference) 的变量可以共享同一个寄存器.

图染色问题的定义在此不作说明. 下面给出 干涉 的定义:

注意如果在某时刻, 上一个变量的生命周期恰好结束而下一个变量的生命周期刚刚开始, 则我们 不认为 这两个变量之间发生了干涉.
而我们一般使用 自顶向下染色 的方式构造 $k$-染色: 先排序, 然后从高到低依次为节点染色.
回顾 Lab3, 我们使用的排序策略是基于编号和邻居数量的复合策略.
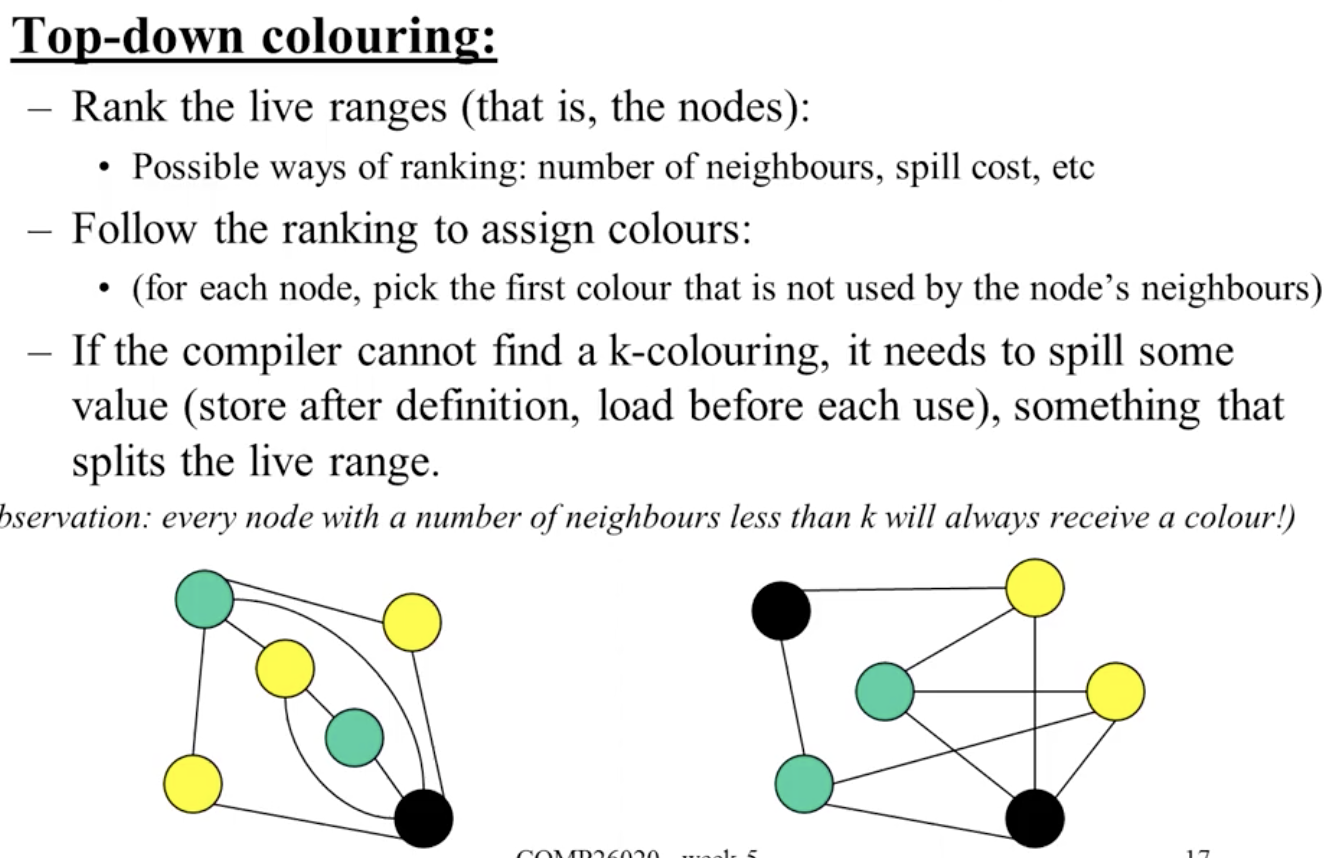
此外, 自底向上染色的方式也很常见.
使用控制流图检测全局生命周期

指令调度 (Instruction Scheduling)
我们最后讨论指令调度.
由于任何指令从执行到返回结果都不可避免地需要耗费一定的时间, 因此通过合理的安排指令调度, 我们就可以优化指令执行所需要的时间, 这也是指令调度的主要目的.

在执行指令调度时, 编译器已经预先知道不同类型的指令对应的延迟数据.

而由于现代计算机可以在同一个周期中执行多条指令, 且指令的结果必须在延迟后才能返回, 因此可以利用这一特性进行一些以提高寄存器利用率为代价的, 针对性的优化.

举例而言, 在下图所示的例子中, 右侧的优化通过增加了一个对寄存器的引用使得我们可以减少三个周期 (恰为 load 的延迟长度) 的程序运行时间.
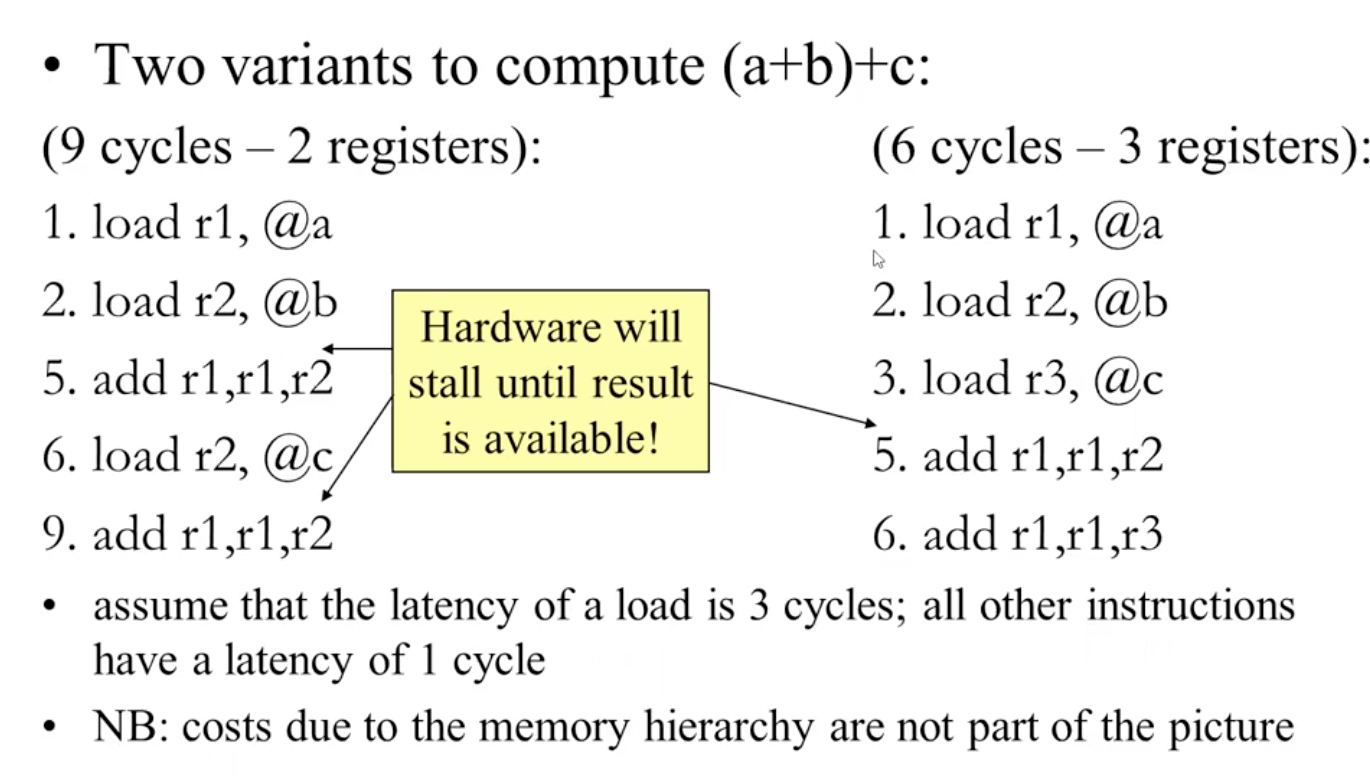
下面介绍对 Basic Block 的指令调度的优化技术:
其基本思想是构造 优先图 (Precedence Graph / Data Dependence Graph), 为图中的每个节点使用某个 优先函数 (Priority Funtion) 计算优先权重, 然后使用 List Scheduling 的手段构造指令调度.

注意优先图考虑的是 每一条指令之间的依赖关系, 而非 寄存器数据之间的依赖关系. 如下图所示:
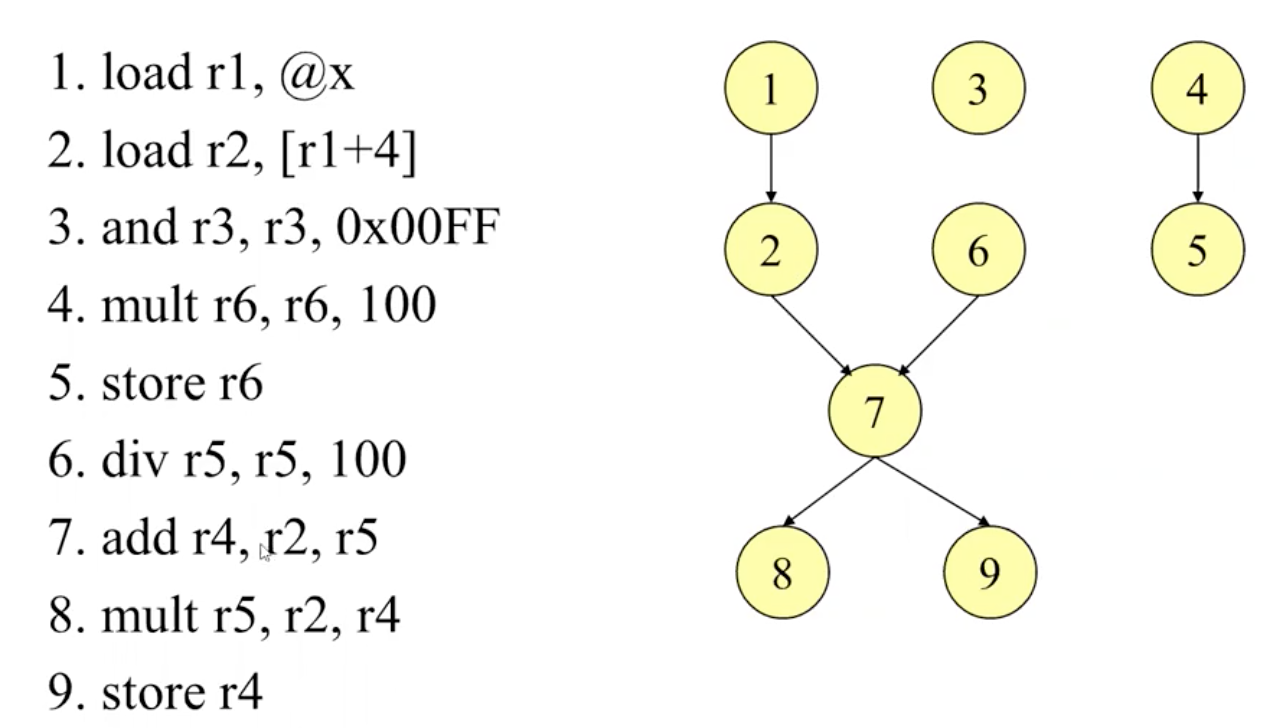
在得到优先图后, 就需要对图中的每个节点进行优先权重的计算:
在下面的例子中, 我们假定每个节点的权重都等于该节点代表指令本身的延迟 + 其所有子节点中最大权重的值. 因此, 优先图的构建是自底向上的:
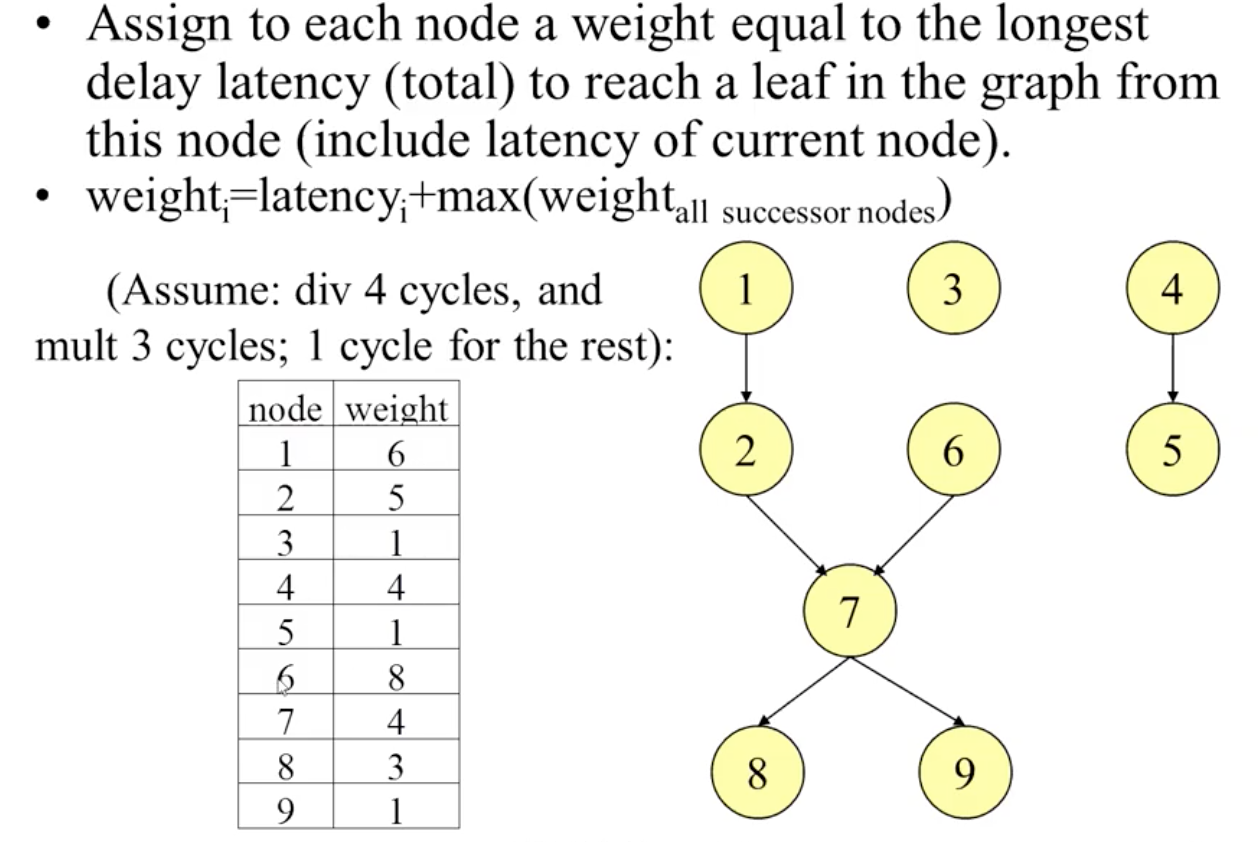
随后我们就可以开始构建指令调度顺序. 首先考虑优先图中没有任何依赖的全体节点, 最先执行权重最大的, 在本例中为 $6$.
随后, 将上一轮中被考虑的那些剩余节点以及 执行了 $6$ 之后满足依赖条件可以被执行的新节点 放在一起按照权重排序, 仍然选择权重最高的优先执行 (在本例中, 因为 $7$ 需要同时满足 $2$ 和 $6$, 因此只执行了 $6$ 之后也不能执行任何新节点, 所以选择 $1$).
依次判断推导, 可知第三步中需要考虑的节点为 $2, 4, 3$, 而在此之中 $2$ 权重最高.
最后可得下图所示的调度顺序:
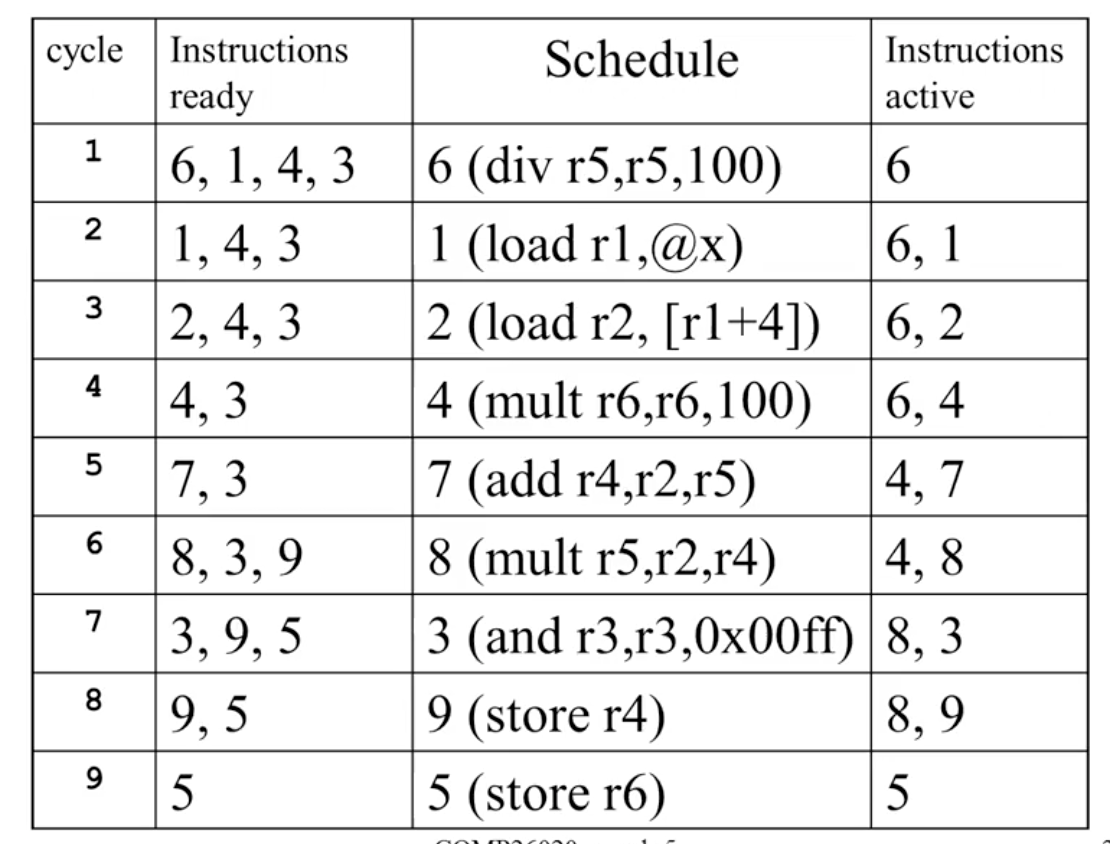
此外, List Scheduling 还可以结合多种优化手段. 此处不再详细介绍:

最后我们可以将编译器的完整结构总结如下:
相关题目解析


($\uparrow$ 64x+16x-x)

($\uparrow$ 函数调用不视为branching)
