单纯形法
单纯形法 (Simplex Algorithm) 是一种用于 求解线性约束问题最优解 的有效算法.
本章介绍 单纯形法. 我们首先通过介绍线性规划问题的图像化表示引入单纯形法的基本思路, 介绍单纯形法中的一些定义, 并通过例子说明使用它求解线性规划问题的操作流程.
单纯形法的引子: 线性规划问题的图像化表示
我们下面回顾 线性规划问题的图像化表示. 考虑下列问题:
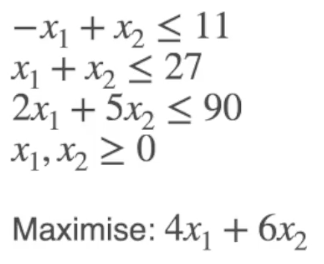
将约束式的边界条件视为一次函数并将其在平面直角坐标系上绘制出来, 不难看出各约束条件所限制的, 平面可取区域的重叠处:
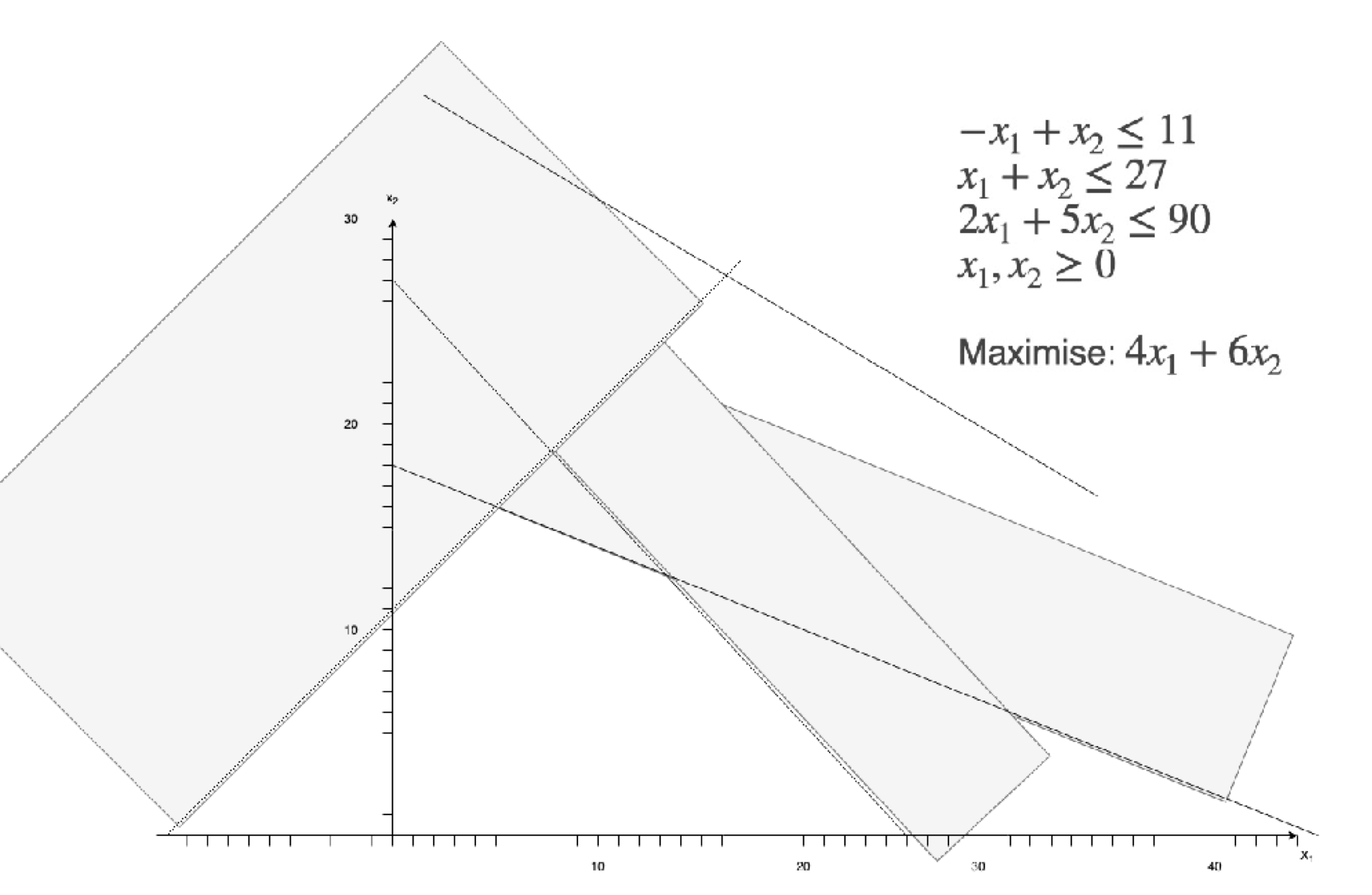
此问题中的可取区域为 $x_1$ 的正方向, $x_2$ 轴和所有一次函数所围成的区域.
显然, 可取区域包含了原点: $(0, 0)$. 我们将介绍适用于这种情形下的线性规划问题最优解计算方法, 而对 可取区域不包含原点 的线性规划问题的求解问题则在下一周内容中讨论.
解决原点为可行解的线性规划问题: 简易单纯形法
单纯形法的基石: 简易单纯形法的基本原理
简易单纯形法的基本原理是: 形如 凸超多边形 的可行域的 顶点之一 必为最优解. 因此:
-
为了确保可行域形为凸超多边形, 单纯形法要求被求解的线性规划问题在矩阵表示形式下满足
\[\mathbf{b} \geqslant 0\]也就是说线性规划问题在被转换为标准形式前, 其表示中不会出现 $=$ 或 $\leqslant$.
-
基于第一点的约束, 不难看出在满足上述条件的问题下 $0$ (零向量, 对应平面的原点) 必为该类问题的一个解.
由于时间关系, 此处不再介绍详细推导过程.
单纯形法中的重要定义: 松弛形式和基础/非基础变量
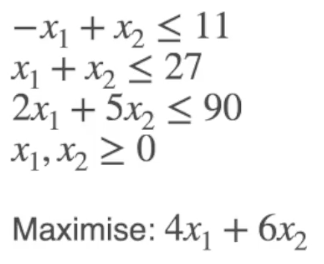
还是考虑上面的例子, 显然这是一个可被单纯形法解决的问题.
在该问题中, 前三条规则 (也就是实际的约束规则) 约束了不等号左边的式子 最多取到某个数值.
因而, 我们可以认为实际上左边的式子和右边的数值之间 存在一定的空隙.
所谓的 松弛形式 就是指, 我们为每一个这样的式子额外引入一个表示空隙的变量, 称其为 松弛变量.
因此, 上述问题的 松弛形式 就是:

注意:
- 对于限制变量为非负的约束规则 (也就是途中从上往下数的第四条规则), 不需要引入任何松弛变量.
- 对于任何其他的约束规则, 都 只引入一个 约束变量.
- 任何约束变量的系数 都是 $1$.
随后补充 基础变量/非基础变量 和 基础解 的定义:

寻找线性约束问题的最优解: 利用松弛形式 (Slack Form)
在上一节中我们介绍了 基础变量 的定义, 显然可知:
- 所有的松弛变量 都是 基础变量
- 约束问题中所有的原始变量 都是 非基础变量.
进一步地, 可以观察到 若兑换某个基础变量和某个非基础变量 时, 我们就可以在图形化表示上得到不同的相交点, 这些相交点如果是坐标系里表示问题可行域的多边形的顶点, 则它就是问题的其中一个解.
由此, 理论上我们只需要不断地对换基础变量和非基础变量, 就可以尝试问题的全部可行解, 最后就能得出问题的最优解.
在下面的单纯形法操作中, 我们会进一步了解它使用了什么样的启发式原则选择可能的最优解从而避免盲目遍历的.
其次, 我们可以进一步思考一个问题: 如果将线性规划问题的松弛形式表示为线性方程组的话, 对换基础变量和非基础变量的过程和 高斯消元法 是否有几分相似, 或者说它其实就是高斯消元法呢?
下面讨论单纯形法的操作步骤:
在单纯形法中遍历可行解: 枢轴 (Pivoting)
所谓的 “枢轴”, 实际上就是在 用增广矩阵表示的, 松弛形式的线性约束问题 中, 在某一步中 基于 某个启发式规则 (具体是什么规则马上会讲) 选定的 某行 和 某列 上的一个元素, 目标是要用这个 “枢轴” 通过 高斯消元法 消去同一列中 包含目标行在内的 所有 非零元.
而在执行这个步骤后, 这个 枢轴 对应列的 非基础变量 和它对应行的 基础变量 之间发生了转换.
下面考虑单纯形法中使用枢轴基于启发式规则快速遍历可行解的方法.
首先启发式规则的定义看下图:

上述截图中的 $\theta$ 就是选择枢轴所在行的依据.
然后以课上的例子结束:

注意在上面的例子中我犯了一个错误: 选定枢轴行后, 需要先使用基础行变换将枢轴的系数变为 $1$.
相关习题解析
见笔记 “数据结构与算法: 复习”.
处理原点不为可行解的线性规划问题: 进阶单纯形法
在上面数节中我们已经知道, Simplex 算法在 原点为线性规划问题的一个可行解 时 必可解决这个线性规划问题. 下面考虑 原点不为线性规划问题的一个可行解的情况:
考虑下面的例子, 显然这个例子中原点不是可行解:
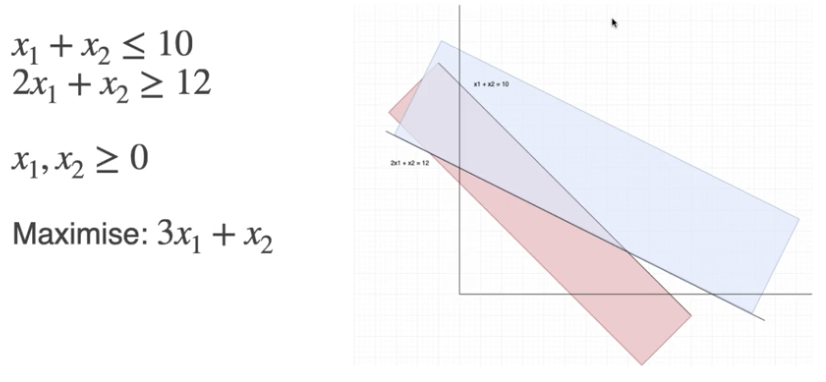
将其转换为增广矩阵表示后也会发现, 在右侧常数列中存在非正数 $-12$, 因此无法使用前面介绍的简易单纯形法求解:
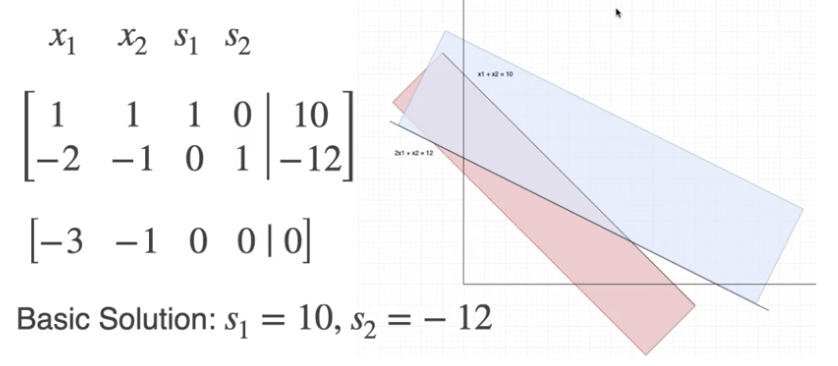
而 进阶单纯形法 处理该问题的基本思路是: 注入 人工变量 (Artificial Variable) 将这个复杂问题转化为一个 接受原点为解的新问题, 并同时 修改问题的优化目标 使 这个人工变量值必须为 $0$, 从而确保 新问题的解也就是原问题的解.

注意对原问题的转换原理:
-
为何这样注入 $a_1$?
“原问题中有个约束式子导致原点代进去值太小, 以至于不为解” -> “注入人工变量 $a_1$, 因为 $a_1>0$, 所以此时 $2 \cdot 0 + 1\cdot 0 + a_1 \geqslant 12$”.
-
为何如此修改目标优化式?
目标优化: 最大化; 另一目标: 让 $a_1$ 为 $0$; => 引入一个数值极大的惩罚参数 $M_1$, 如果 $a_1$ 不为 $0$ 则 经过修改的目标参数式 $3x_1 + x_2 - M_1 a_1$ 永为 $-\infty$ 得不到优化 => 实现对 “最优解中 $a_1$ 必须为 $0$“ 的约束.
在引入人工变量和对目标约束作相应转换后, 就可以将得到的新问题转化为增广矩阵表示, 然后只需先选 $a$ 不为 $0$ 的行作为枢轴, 同时让负参数变为 $1$, 并 pivot out M, 就把问题转换成了简易 Simplex 问题, 然后就可以用原来的技术求解.
注意此处有多少个约束式导致原点不为 $0$ 就需要相应引入多少个人工变量 $a$ 和惩罚参数 $M$, 后续也就要分别用 Pivoting 干掉多少个 $M$. 至于为何任何式子中最多只能注入一个人工变量, 由于过于显然笔者拒绝解释.
详细的注入/转换规则和对应的例子看下图:

线性约束问题解空间无界 (Unbounded) 的情形
下面讨论如何处理 解空间无上界 (Solution Space Unbonded) 的线性约束问题:
考虑下面的例子:
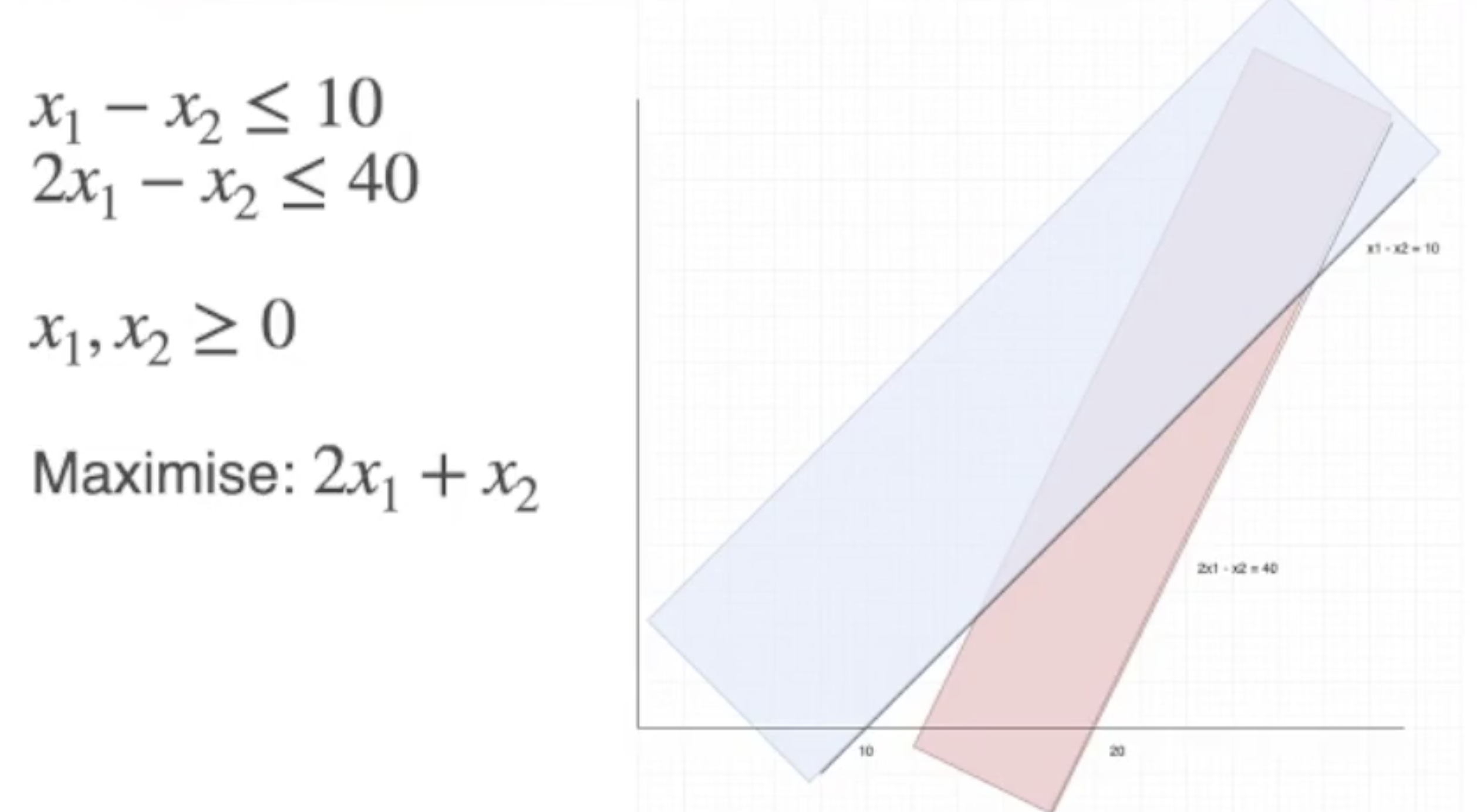
如图所示, 两个约束条件代表的可行域 (蓝色部分和红色部分) 虽然有相交区域但 并未和 $x$ 轴或 $y$ 轴形成封闭区域, 问题的可行域并非是封闭图形, 因此不但解的数量没有上限, 还可以观察到变量 $x_1$ 和 $x_2$ 的取值可以是非常大的, 没有上限.
如果使用常规单纯形法尝试解决该问题的话, 会出现 所有的候选 exiting variables 都有 negative slack 的情况:
这实际上意味着, 在本问题中我们已经 遍历完了所有的可行域顶点, 但因为我们尚未找到解 (优化目标行仍然有负系数), 因此我们还没有找到问题的最优可行解. 因此, 该问题是 unbounded 的.
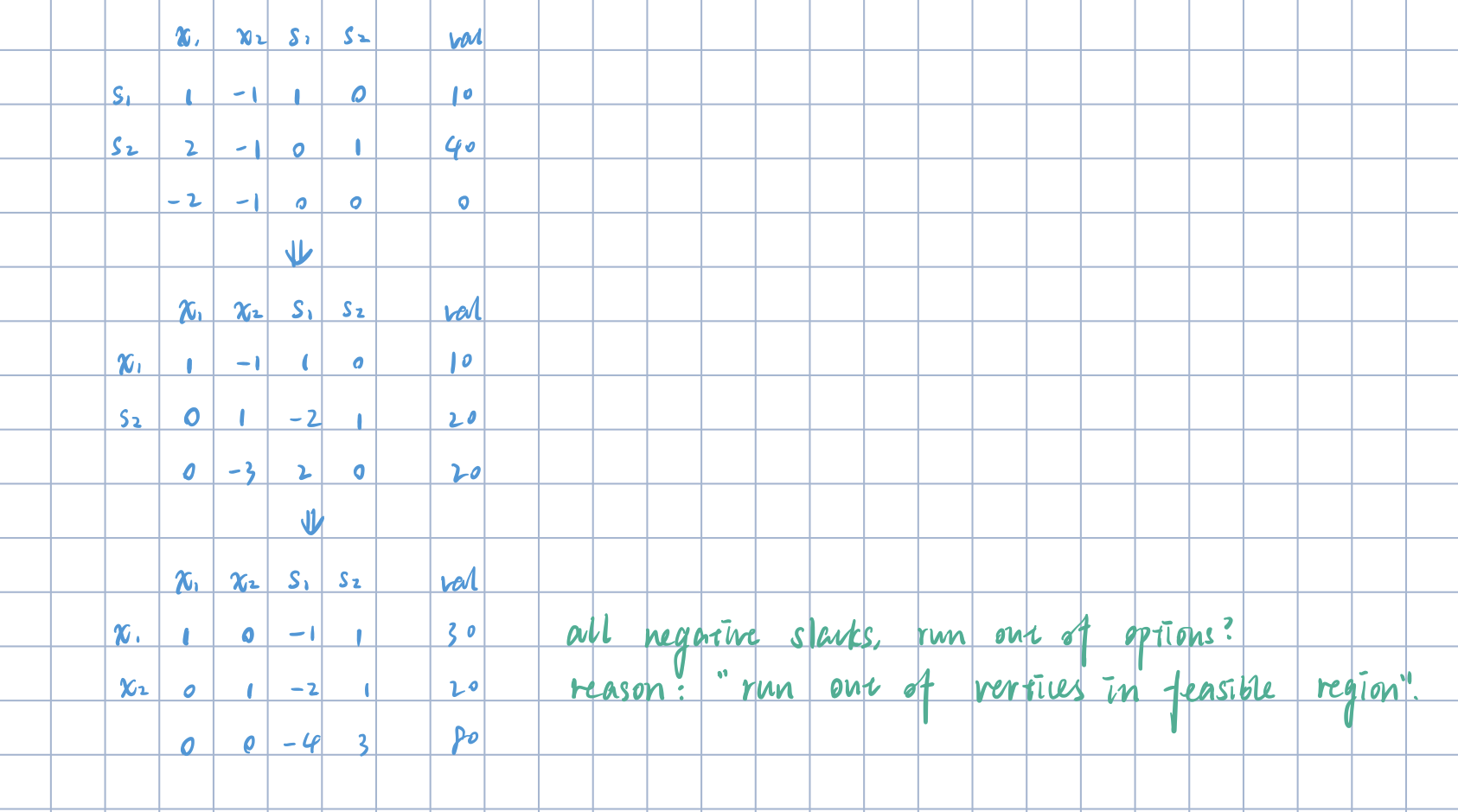
实际上一般地, 如果我们发现问题的增广矩阵表示中某个候选变量的一整列系数都为负值的话, 往往就意味着这个问题是一个 Unbounded Problem.

Zero Slack: Degeneracy 问题
进一步地, 我们可能会遇到这样的问题:
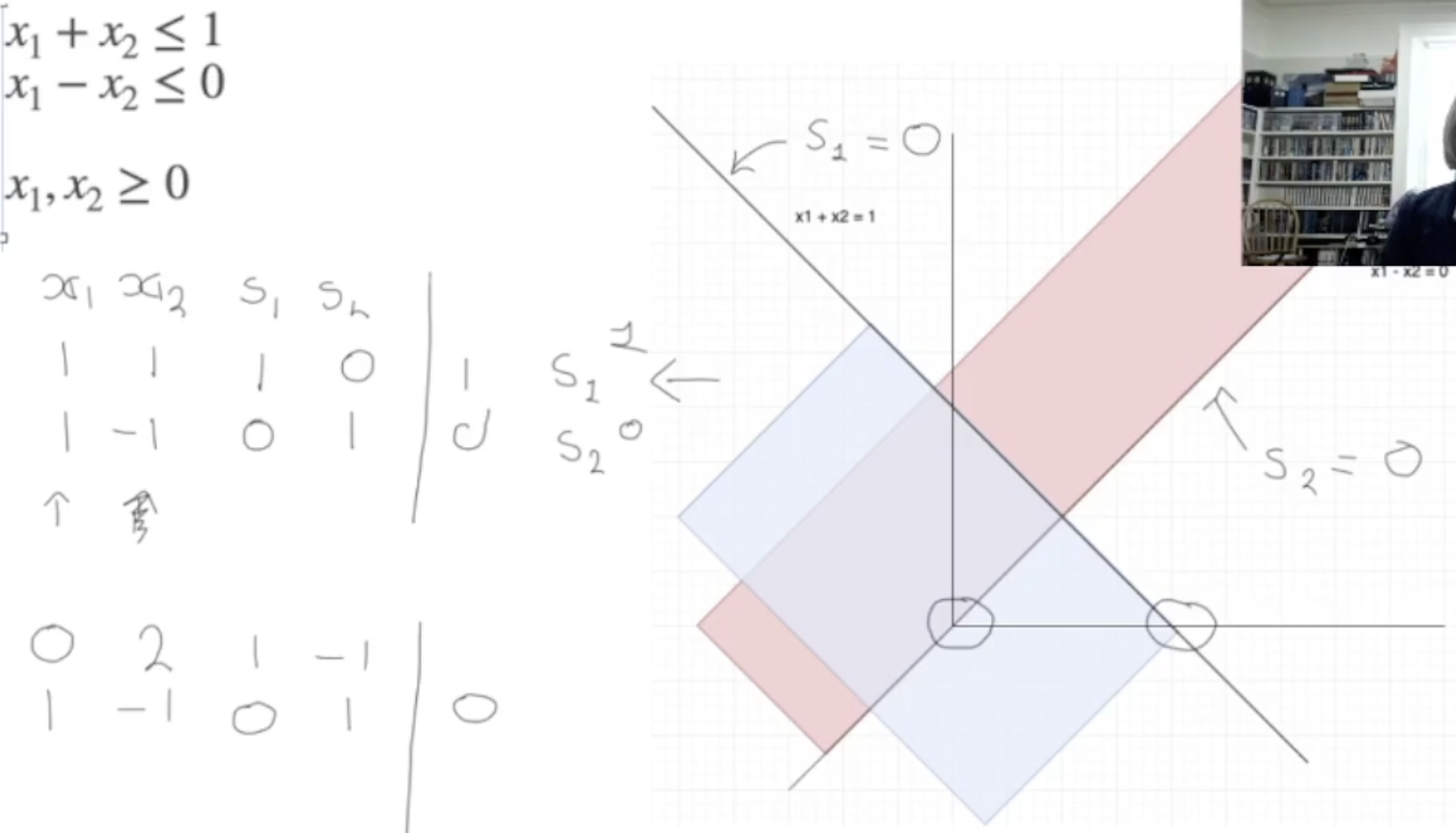
如上图所示, 在计算备选的 exit variables 时, 计算出有些 slack 为 $0$, 注意此时需要 优先选择 slack 为 $0$ 且变量系数非负, 而且更小的对应行.
” Towards the end of this video I state that, in the case of a choice of leaving variables with zero slack and a positive coefficient in the column for the entering variable you should chose the variable with the largest positive coefficient - this should be smallest positive coefficent (see the reading).”
case1: 若无 zero slack variable with positive coefficient, 选择 $\theta$ 为正数 最小的那个. (注意 $\theta$ 的计算方式: slack variable / coefficient,)
case2: 存在一些 zero slack variable with positive coefficient, 此时选择 entering variable 对应列系数 为正且最小的 那一行.
相关习题解析:
见笔记 “数据结构与算法: 复习”.
補充問題: 單純形法的時間複雜度
在最壞情況下: $O(2^n)$ (此時 $n$ 為變量數量. 具體原因是: 在最壞情況下單純形法需要遍歷 “平面” (在高維情況下需要遍歷的是 “超立方體”) 的 所有節點, 而由於 該原因 一個包含 $n$ 個 base variable 的單純形法的可行域是 $n$ 維 的, 對應空間內的超立方體有 $2^n$ 個頂點), 因此需要遍歷所有的 $2^n$ 個節點.

