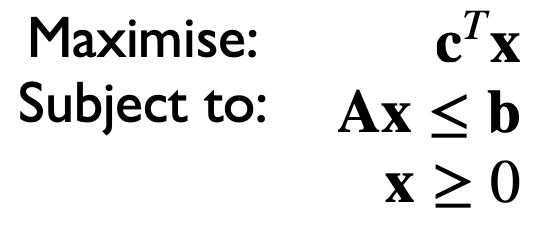线性规划
本章将引入线性规划问题的一般概念并讨论表示它们的不同方式.
1. 线性规划问题的定义和表示
我们称 线性规划问题 为: 在给定一系列 约束条件 的前提下, 要求 最小化或最大化某个评价参数 的 优化问题.
一般地, 一个标准的线性规划问题由下列的元素组成:
-
具线性表达形式的问题需求
\[a_1x_1 + \cdots + a_nx_n\] - 由不等号 (如 $\leqslant$, $\geqslant$) 表示的 约束关系
- 均大于等于 $0$ 的变量
考虑下面的这个简单例子:
假设某个农民有数量为 $F$ 和 $P$ 的肥料与农药, 可供耕种的土地容量为 $A$, 规划种植小麦 (Wheat) 和大麦 (Barley) 的量设为 $x_W$ 和 $x_B$, 这两种农作物的单价为 $S_B, S_W$. 而单位小麦和大麦所需要的肥料量与农药量分别为 $F_W, F_B$ 和 $P_W, P_B$. 问: 如何规划种植小麦和大麦的数量使得获利最多?
将上述的问题解释为线性规划问题, 则有如下的表示方法:
首先我们需要优化的对象是总获利:
\[S_B\cdot x_B + S_W \cdot x_W\]其次, 我们有下列的三个约束:
- \[x_B+ x_W \leqslant A\]
- \[F_B \cdot x_B + F_W \cdot x_W \leqslant F\]
- \[P_B \cdot x_B + P_W \cdot x_W \leqslant F\]
这三个约束分别表示:
- 对这两种作物的规划种植量恰好不超过土地的承载能力.
- 持有的肥料恰好满足这两种作物的需求.
- 持有的农药也恰好满足这两种作物的需求.
2. 线性规划问题的求解
我们进一步将上一节中提及的种植规划问题形式化, 将问题中的 优化目标 和 问题约束 形式化为 目标式 和 约束式:
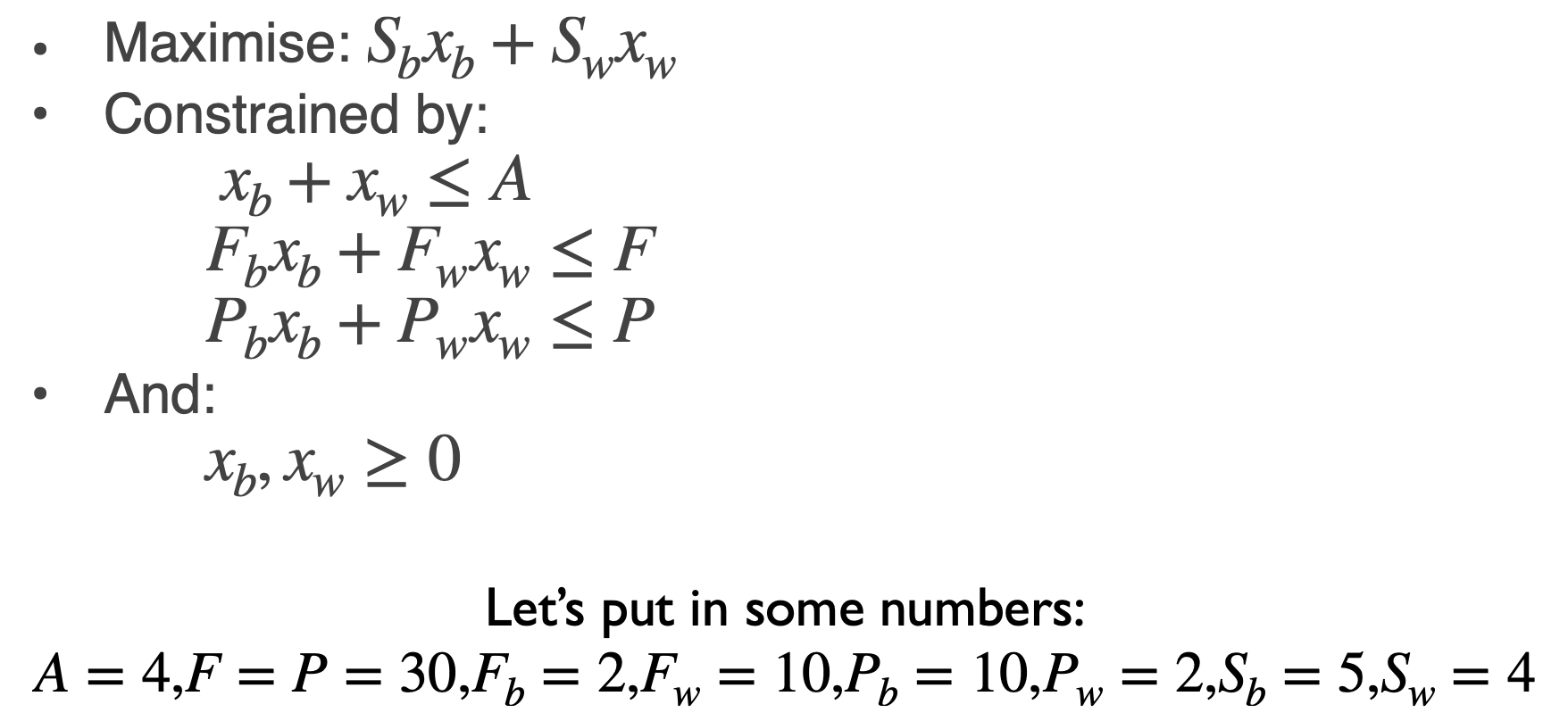
因此有:
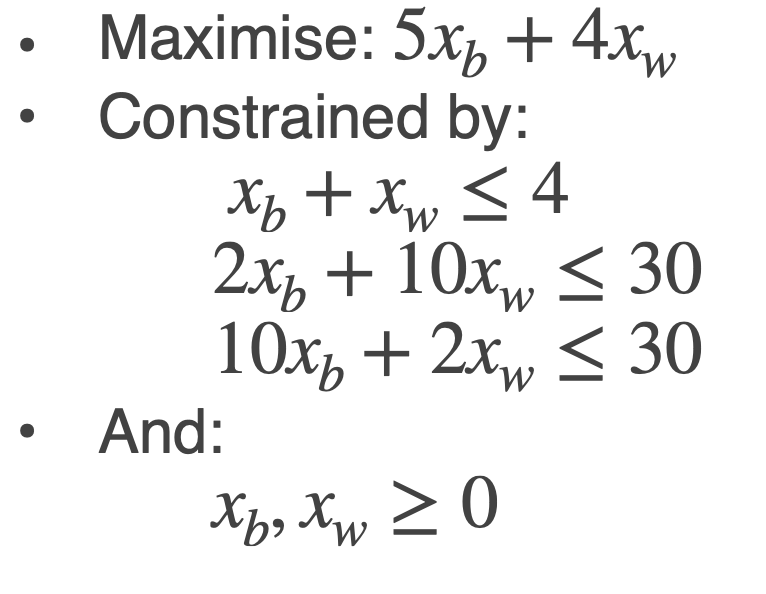
3. 线性规划问题的矩阵表示法
线性规划问题除了可以表示为上述的标准形式外, 还可以使用矩阵表示法表达.
考虑下列的线性规划问题:
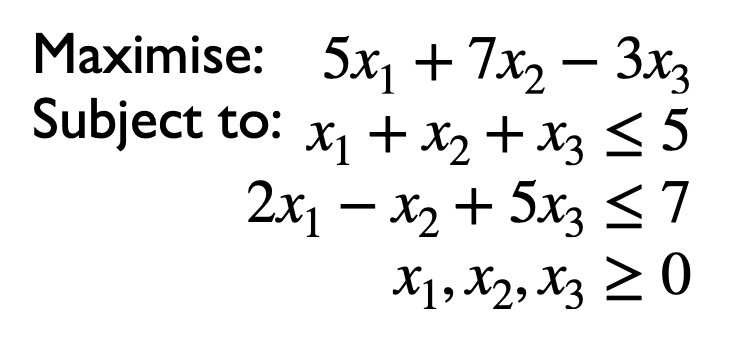
在将该问题从标准形式表示转换为矩阵表示前, 首先将所有公式 (无论是目标式还是约束式) 中变量的顺序调整到完全一致, 如上图中的顺序 $x_1, x_2, x_3$.
然后, 就可以将变量和常数全部分离为列向量或矩阵, 如下图所示:
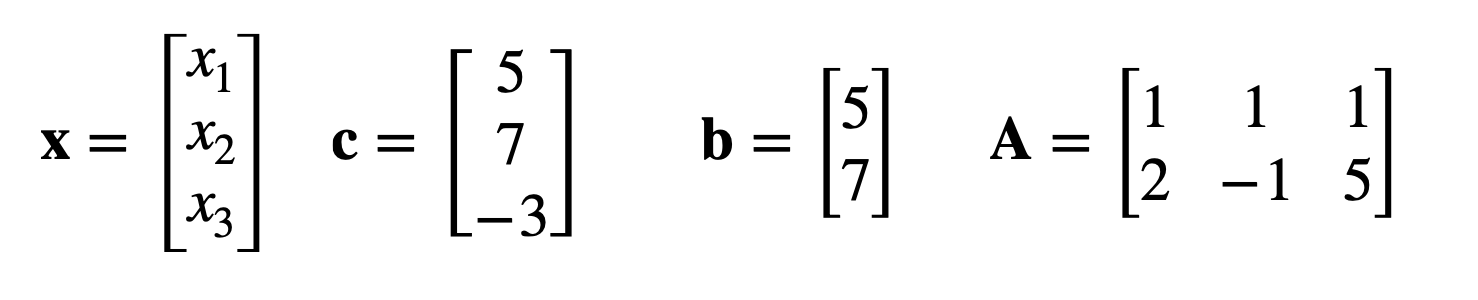
此时该问题就被转换成了下面的形式: