投影
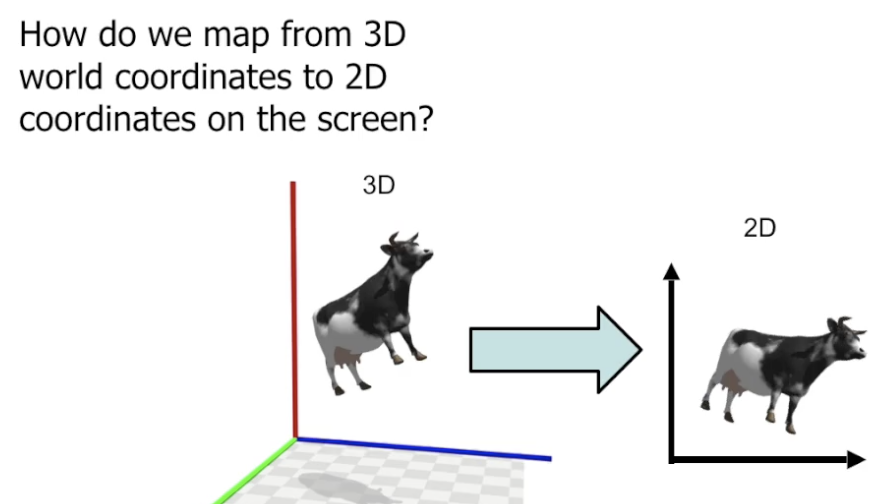
在上面一节中, 我们已经完成了对于 “如何在二维视场中观察三维和二维世界” 方法的讨论. 下面我们着重考虑 在二维视场中观察三维世界, 讨论不同的 投影 (Projection) 方式.
这一步在三维观察管线中, 恰位于第三步 (投影变换), 完成了模型变换和视角变换之后.
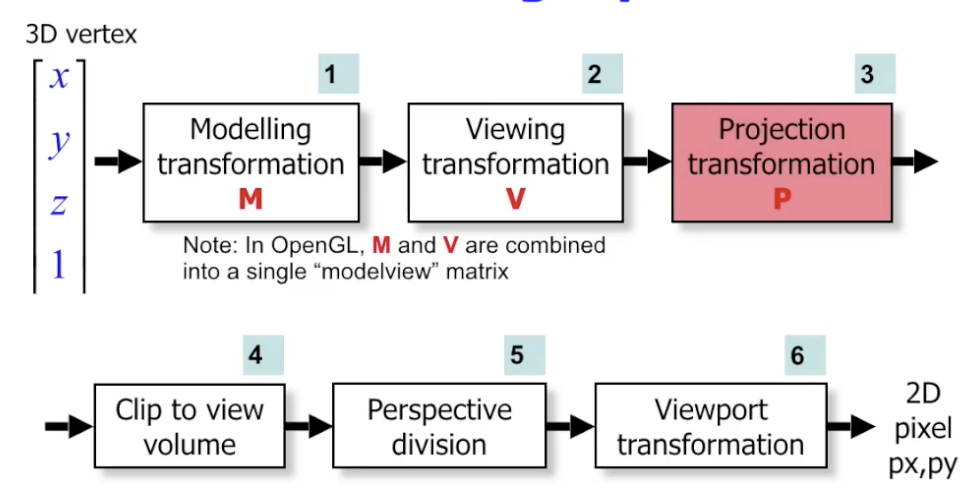
这里的投影问题实质上是 平面投影问题 (Planar Geometric Projection). 而我们即将讨论的投影类型分为 平行投影 和 透视投影, 二者 都保持所有直线, 前者保留原图形中 所有边的平行关系, 而后者符合肉眼观测中 近大远小 的常识.
除此之外, 也有其他 不保持直线 的平面投影方法,
平行投影 (Parallel Projection)
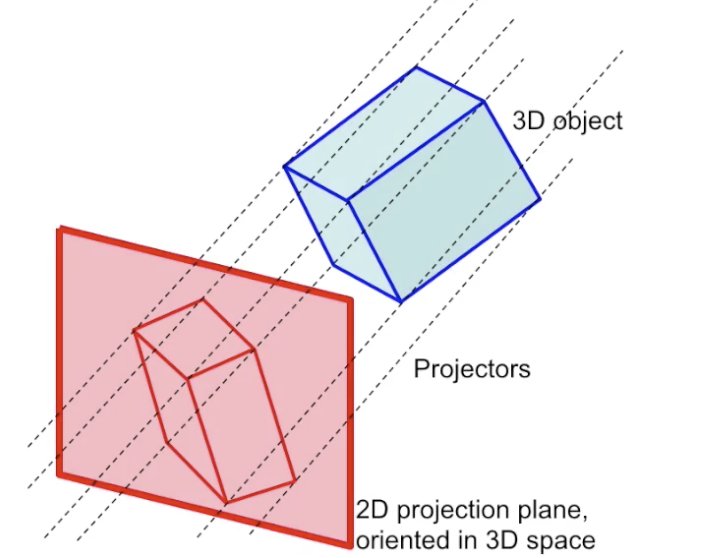
在平行投影中, 我们假定 任何光线均平行, 投影出的图形是 经过平行光投影 得到的结果, 原图像中的 任何一对平行线 在经过投影后得到的图形中 仍然对应平行.
正交投影 (Orthographic Projection)
三视图
首先, 三视图属于正交投影的一种. 在三视图中视角总和坐标系中某一坐标轴垂直, 因此三维空间中的三视图分为 正视图, 侧视图 和 俯视图:
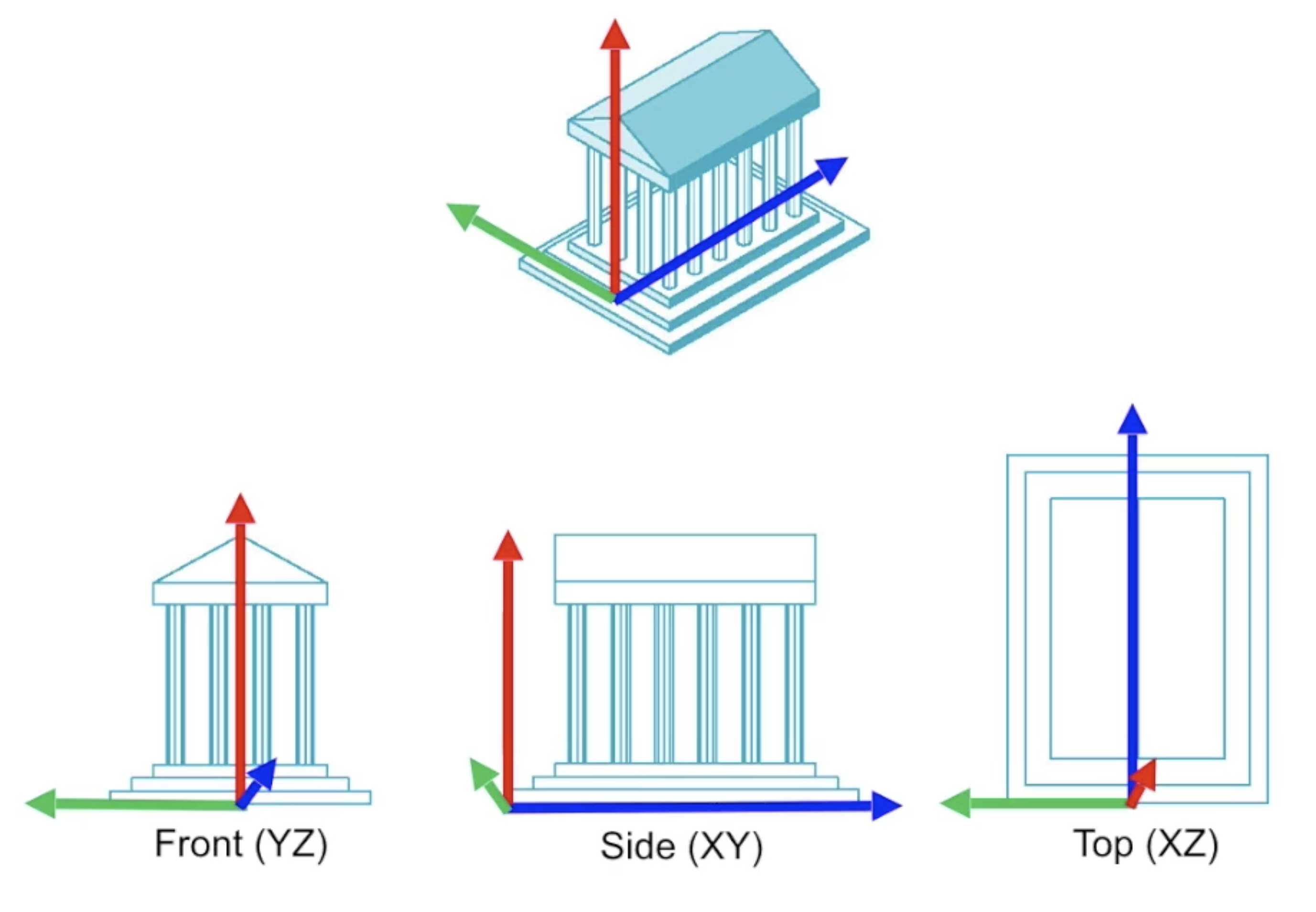
三视图投影变换非常简单, 只需将所有像素点坐标中对应维度设为 $0$ 即可. 注意显然三视图投影是丢失了一整个维度信息的, 因此其变换矩阵自然是 Singular 的, 变换 不可逆.
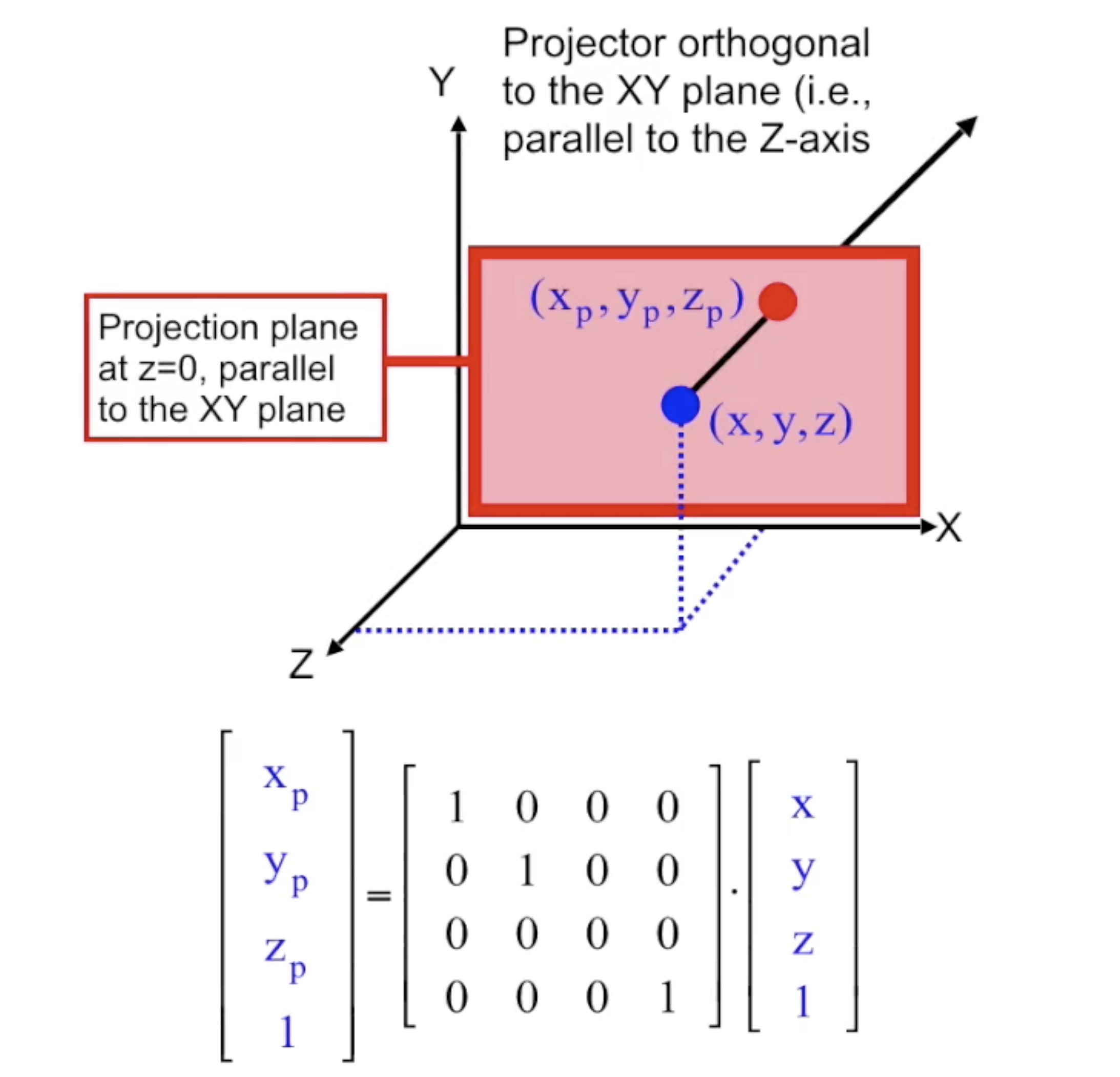
斜轴侧投影 (Axonometric Projection)
另一种正交投影为 斜轴侧投影. 在斜轴测投影中, 可能出现某些或全部坐标轴的缩放变形. 根据坐标轴是否缩放 (也就是比例是否和其他坐标轴相等), 斜轴测投影又被细分为三种:
-
斜等轴投影 (
Isometric Projection):三个轴向伸缩系数相等, 也就是 $x=y=z$.
-
斜二轴投影 (
Dimetric Projection):只有两个轴向伸缩系数相等, 也就是 $x=y \neq z$, 或 $x=z \neq y$, 或 $x \neq y=z$.
-
斜三轴投影 (
Trimetric Projection):\三个轴向伸缩系数均不相同, 即 $x \neq y \neq z$.
注意此处区分三种斜轴侧投影的方式: 关注投影面 (并非无限扩展的平面, 而应该当作一个矩形处理) 能被几条坐标轴等分.
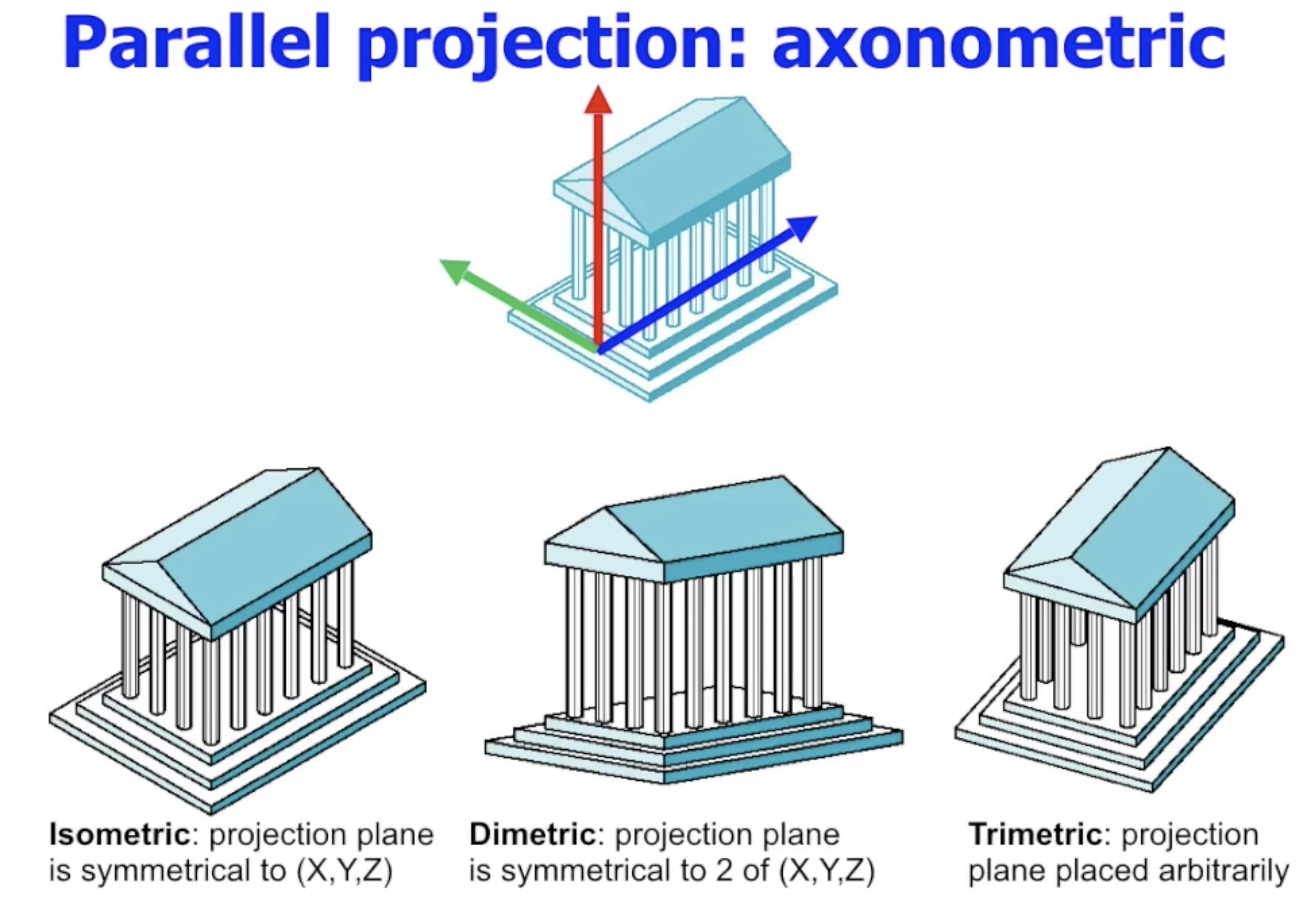
倾斜投影 (Oblique Projection)
倾斜投影是最一般的平行投影, 因其对投影面和三维空间内的坐标轴之间的空间关系没有任何要求. 因此, 在倾斜投影中, 物体的 长度 和 线段之间的夹角 都会被 扭曲.
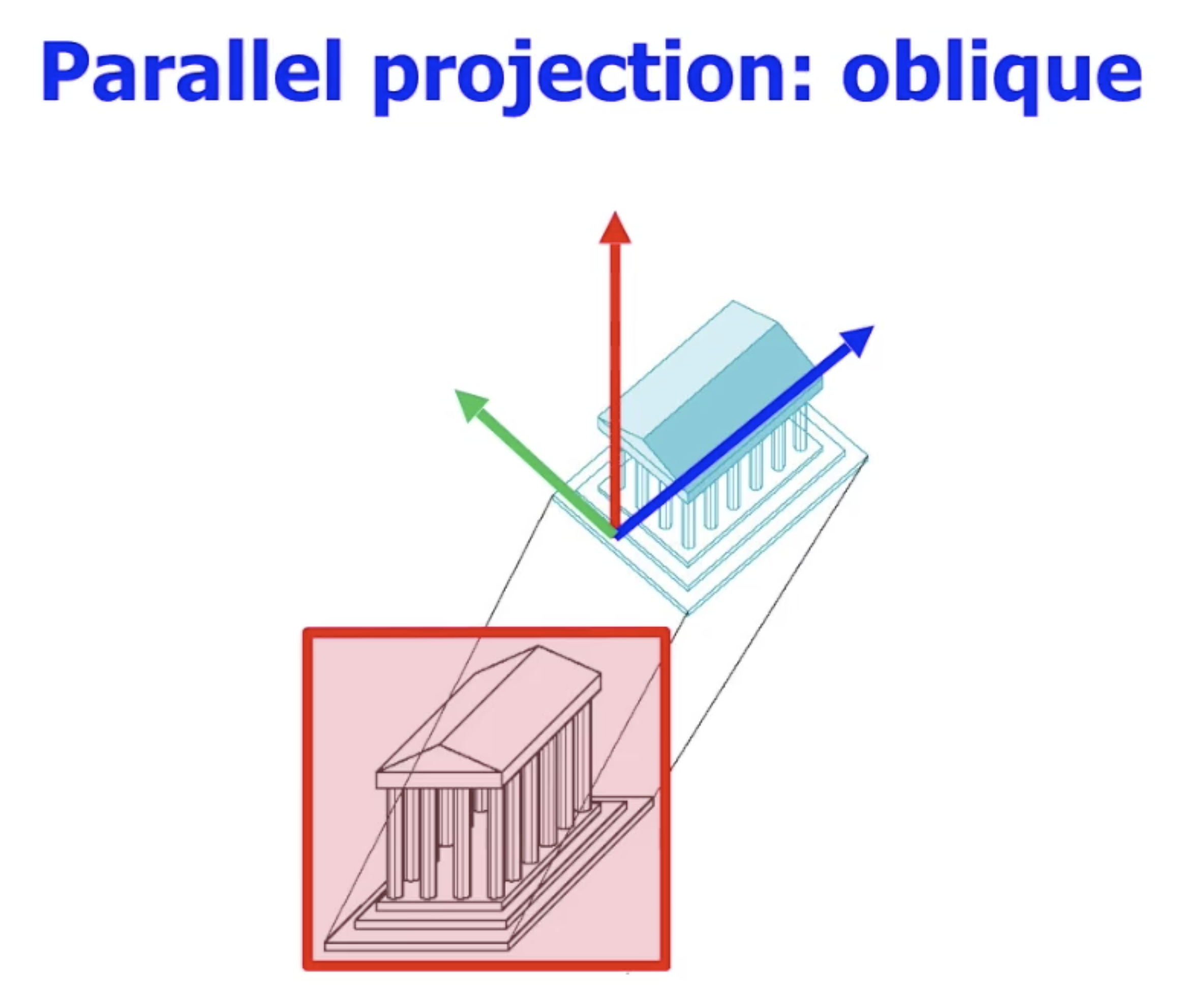
透视投影 (Perspective Projection)
下面讨论透视投影.
透视投影的特点是: 近大远小, 和观察方向平行的平行线最终会无限延伸, 相交于无穷远点, 而垂直于观察方向的平行线则会保持平行关系.
而随着观察角度的不同, 和平行投影相似, 透视投影也 基于平行线汇聚点的数量 分为三种:
1-Point Perspective: 图中平行线如果汇聚, 只会汇聚于一个无穷远点.2-Point Perspective: 图中平行线如果汇聚, 则可能汇聚于两个无穷远点.3-Point Perspective: 图中平行线如果汇聚, 则可能会汇聚于三个无穷远点.
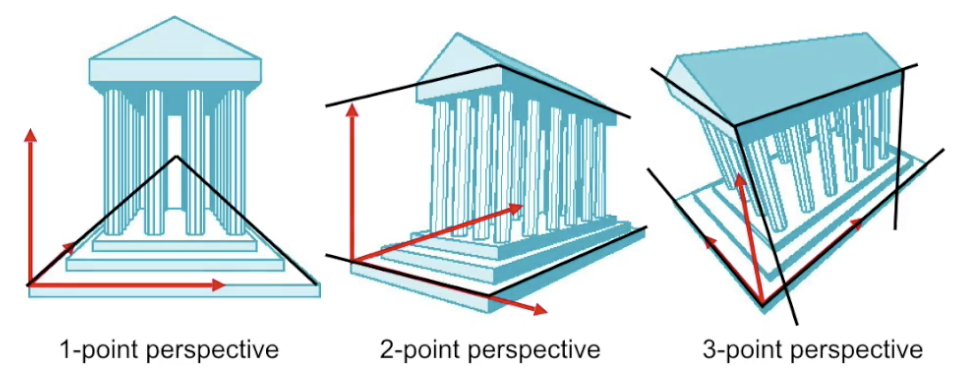
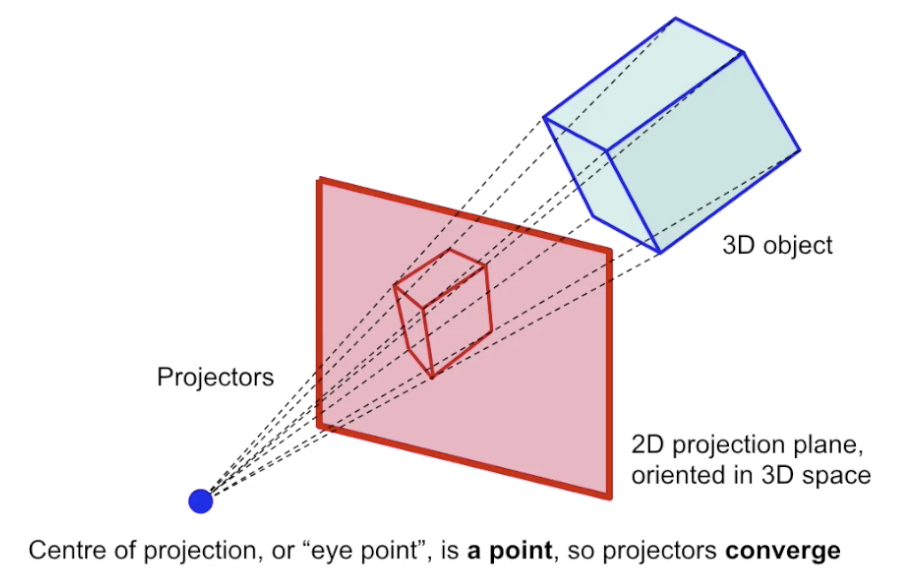
下面考虑如何计算深度不同的点在平行投影下应该被投影到画面上的位置, 简便起见考虑 1-Point Perspective.
假设三维空间中观测点位于 $(x, y, z)$, 投影面 平行于 $x-y$ 轴, 位于距离 $z$ 轴 $d$ 处.
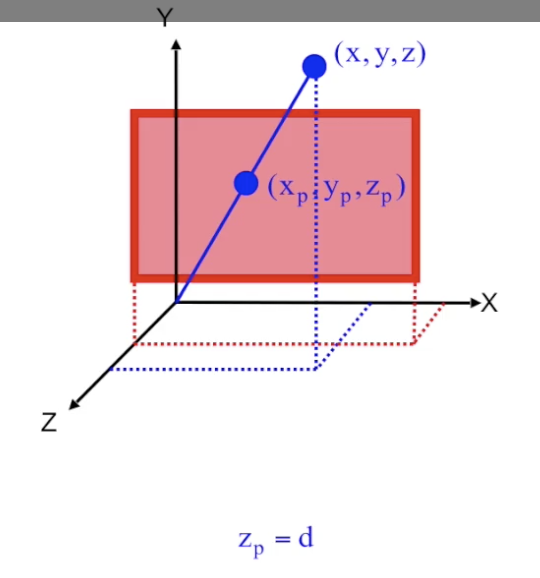
从几何角度考虑, 已知坐标原点和观测点之间连线的表达式, 结合距离 $z$ 轴为 $p$ 这个条件可直接解算出在投影面上对应点的坐标: $(x_p, y_p, z_p)$.
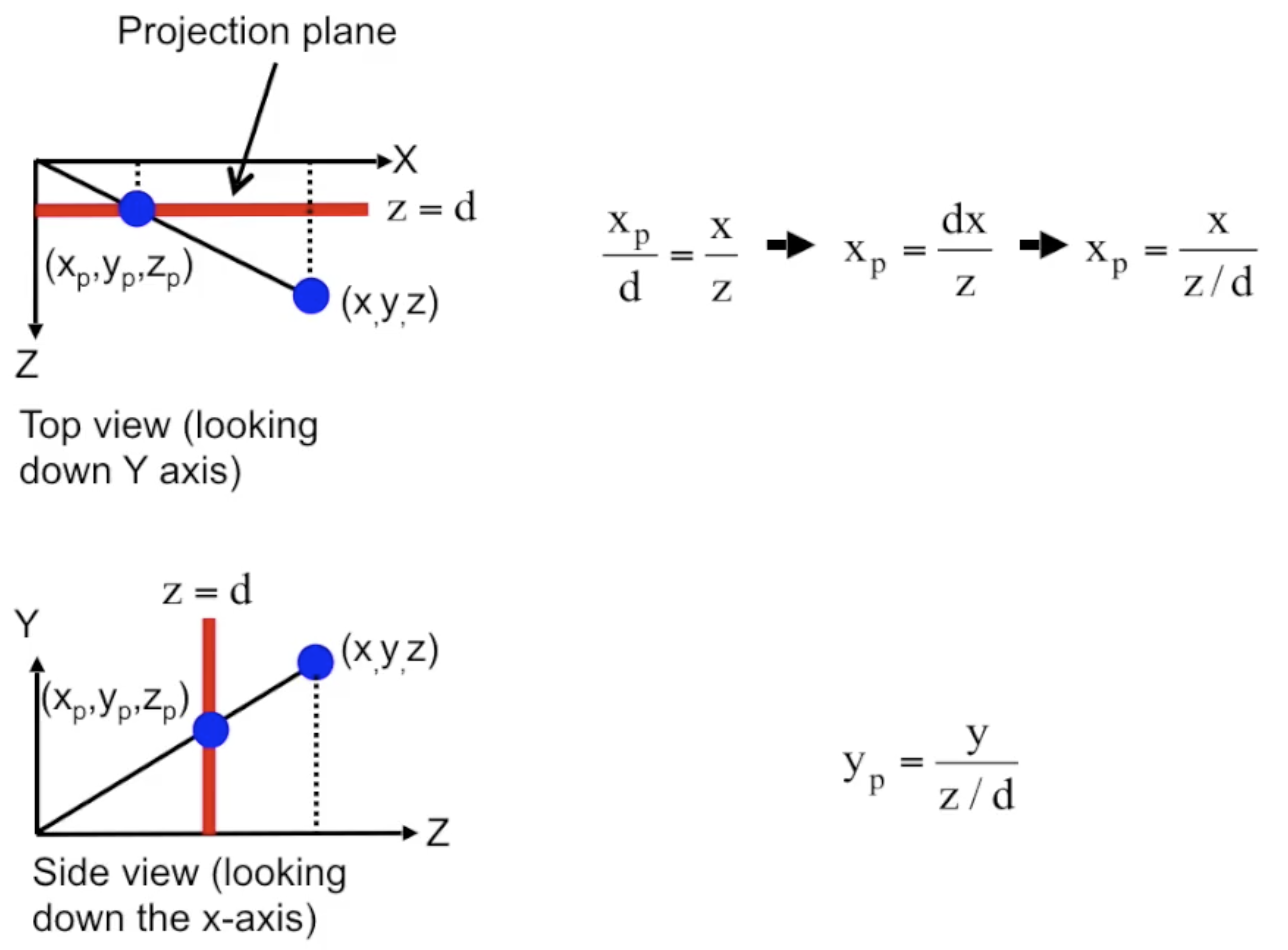
观察到 $x, y$ 轴坐标都有明显的 相同变化规律. 由此可推导出 1-Point Perspective 的投影点坐标计算方法:
首先使用对应的变换矩阵, 然后将变换后得到的向量规范化, 让这个齐次坐标的第四维度恢复为 $1$.
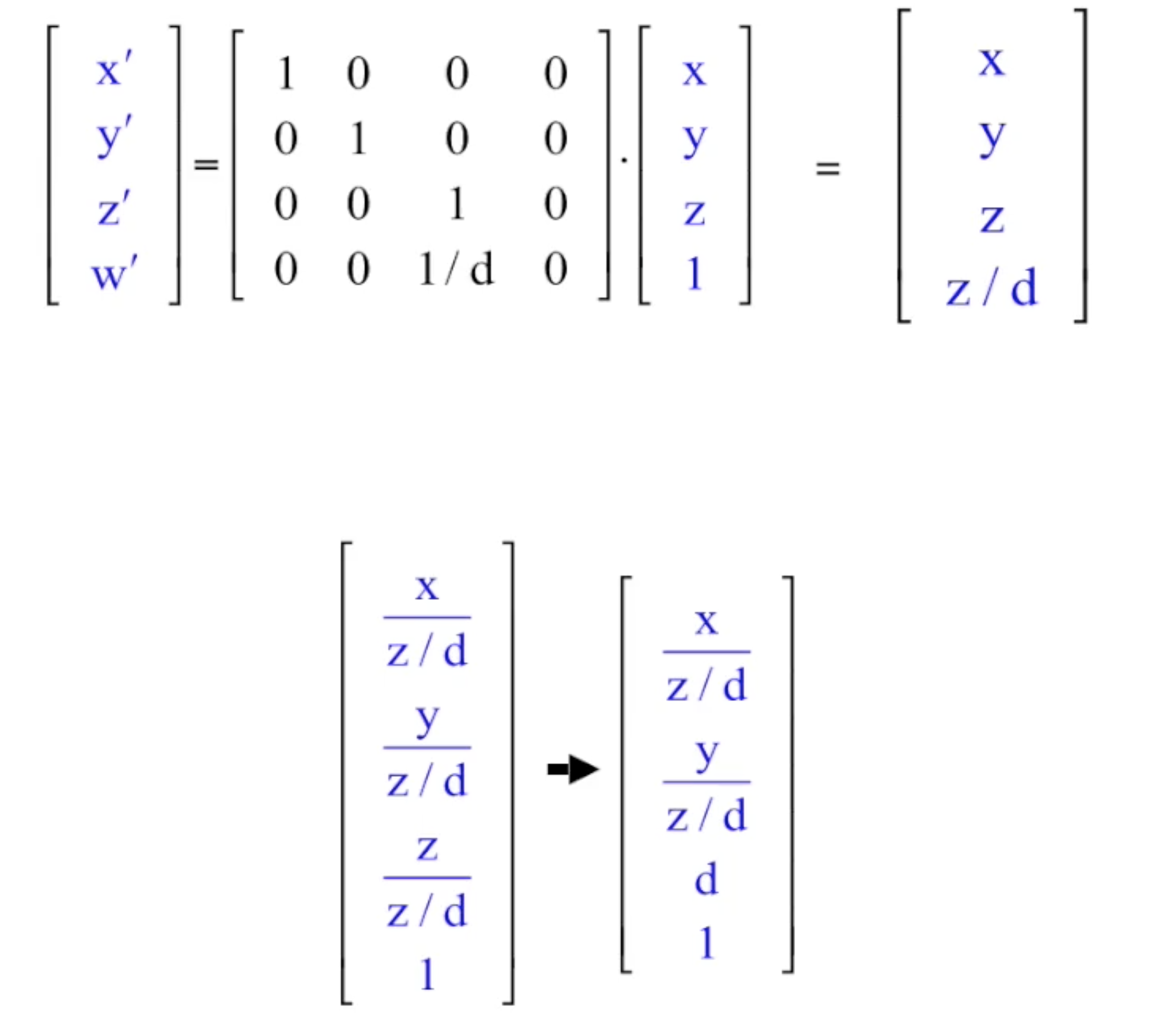
相应地可以用类似的方法推导出 3-Point Perspective 的坐标计算方法:

投影视场 (Field of View)
在透视投影中, 相机能观察到的图形显然是 有范围 的: 相机无法捕捉距离太近的物体, 因为此时基于透视投影原理它显得太大; 相机也无法捕捉距离太远的物体, 因为基于同样的原因它几乎没法被看清. 因此, 我们需要确定透视投影下. 相机在空间中的 观察范围, 它被定义为 视景体.
同时, 由于视景体是 有限大 的, 任何超出视景体的物体或物体的部分都必须被 裁切.

我们下面依序详细讨论这两种定义和技术.
视景体 (View Volume)
视景体定义了相机所能看到的场景 (三维场景) 范围.
平行投影的视景体
对平行投影而言, 由于可视范围有限, 因此视景体的组成中必包括 最近面 (Near Plane) 和 最远面 (Far Plane). 又由于平行投影保持平行关系不变, 因此其视景体就是一个长方体, 如下图所示:
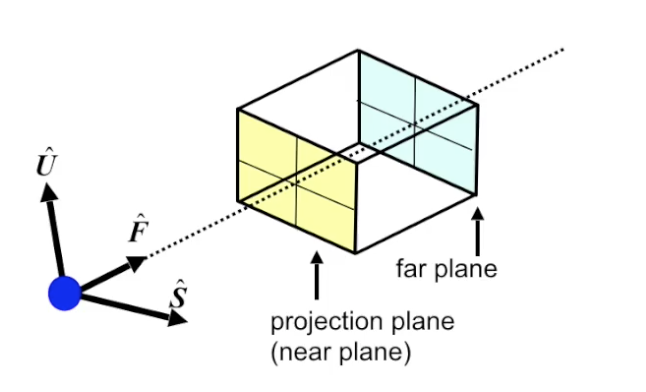
任何位于视景体中的物体都是可见的, 而溢出视景体的物体都不可见.
正交投影的视景体
ThreeJS 提供了 正交投影相机, 它定义的正交投影视景体就是 由 $6$ 个面组成的长方体, 其中最近面也就是实际的投影面.
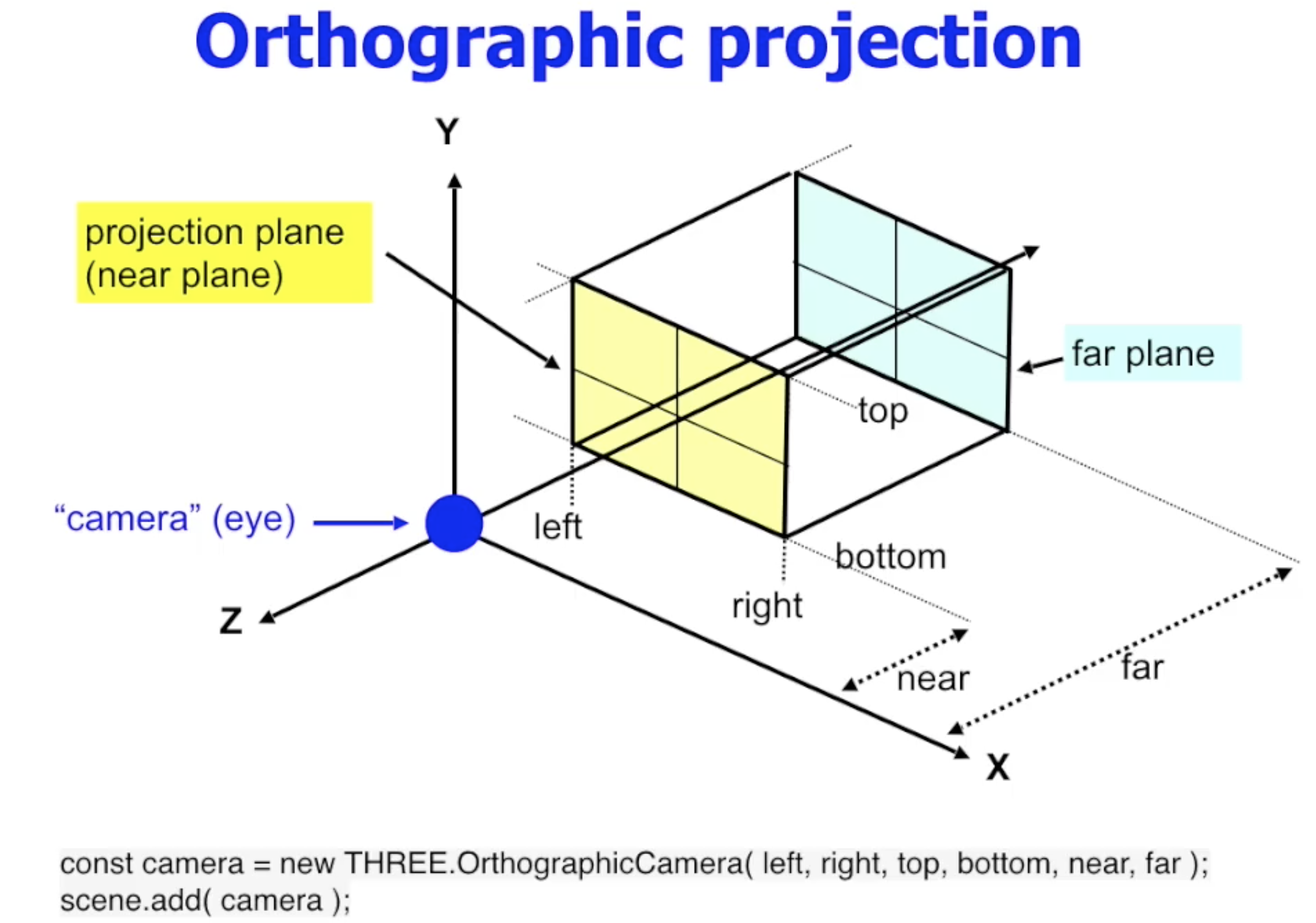
透视投影的视景体
对透视投影而言, 由于平行线至少相交于一点, 因此其视景体是一个 台体. ThreeJS 中对透视投影的视景体定义需要四个参数:
视角, 最近/远面比例, 最近面距离和最远面距离. 已知最近面距离和视角, 显然即可计算出最近面的宽高. 因此我们也可认为, 最近面距离, 视角和面比例共同决定了最近面的形状和大小.
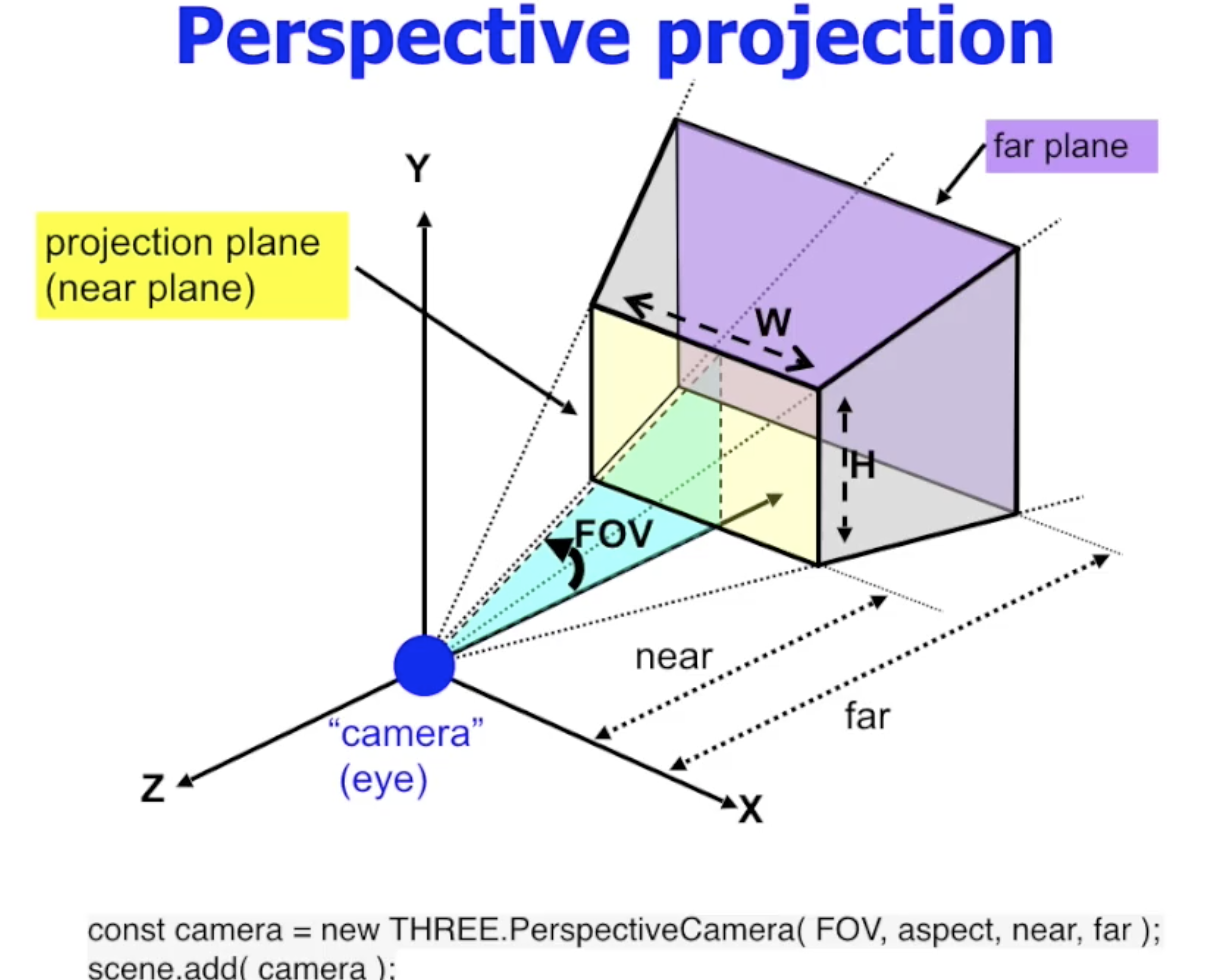
投影规范化: 避免透视变换中的信息损失
回顾透视投影中, 物体在透视投影面上坐标的计算, 可以看到在坐标计算过程中存在不可逆的信息损失, 以 1-Point Perspective 为例, 显然在下面的例子中所有坐标的 $z$ 轴值经过转换全部变成了 $d$, 造成了 $z$ 轴深度信息的不可逆信息损失.

$z$ 轴上的信息损失是不可接受的, 因为我们需要它来作为 $z-buffer$ 的数据源, 用来执行 隐藏面移除.
因此我们引入了 新的透视变换: 投影规范化 (Perspective Normalisation).
其基本思想是: 不直接对三维空间中的物体进行透视变换, 而是先一五一十地在 台体状的视景体 中包含物体, 然后 通过对整个视景体的透视变换 在 保留深度信息 的同时 等效完成对图形的透视变换.
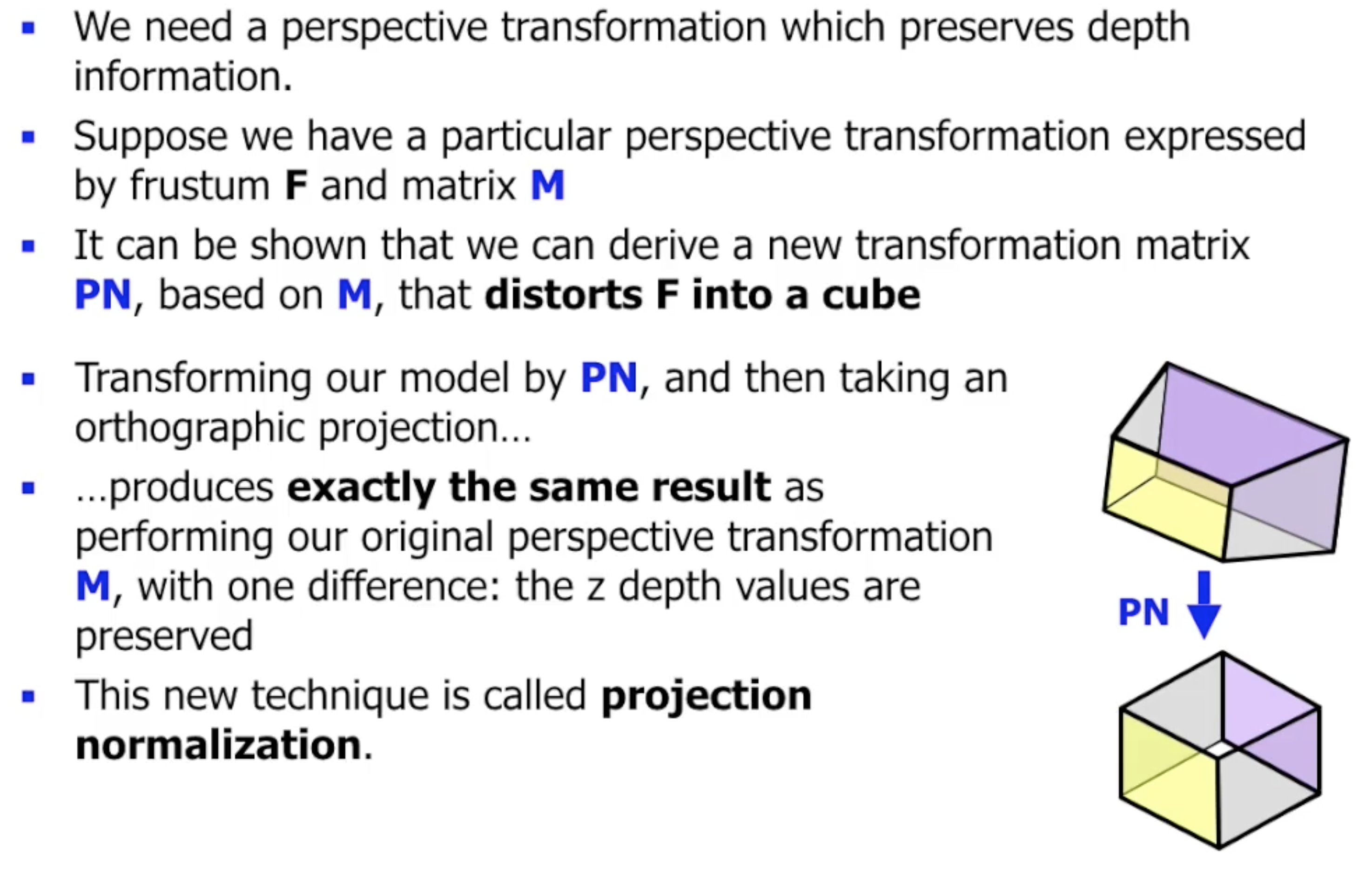
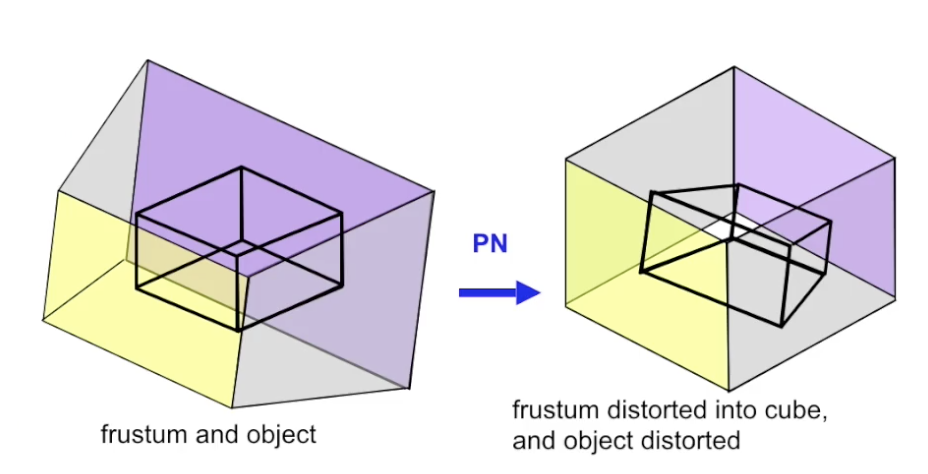
然后, 再对 被投影规范化后, 从 台体变成了长方体 的视景体执行 正交投影, 就可得到完全一致但 保留了深度信息 的结果.
裁切
最后, 我们需要将位于视场外的所有物体或物体的部分移除.
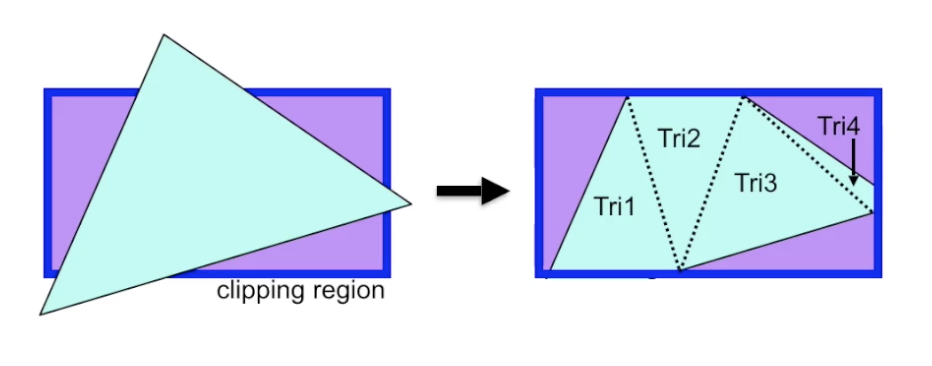
一般地, 上述过程同时伴随着曲面细分, 用来将经过裁切后得到的区域网格化为多个三角形组成的网格.
