最小生成树
本章将引入 最小生成树 (Minimum Spanning Tree) 和 图分割 (Cut of a graph) 的概念, 并介绍数种可用于寻找给定图的最小生成树的算法.
1. 最小生成树的定义与最小生成树问题
如果将单源最短路径问题类比为在现存的铁路网中找到一条从出发地到目的地的, 耗时最短或经停站数最少的路线的话, 最小生成树问题就可视为, 给定所有我们希望连通的站点以及建设站点间连线铁路的成本, 要求给出一个建设成本最低但又能确保连通所有站点的建设规划.
1. 问题定义
定义 1.1 (最小生成树, Minimum Spanning Tree)
对任意给定的有权图 $G = \langle V, E\rangle$, 其 最小生成树 $T = \langle V, E’ \rangle$ 为 总权重最小 的, 恰能连通 $G$ 内每个节点的 树.
显然可知, 图 $G$ 的最小生成树 $T$ 的顶点集与 $G$ 相同, 而其边集为 $G$ 的子集.
下面基于对最小生成树的定义形式化最小生成树问题:
定义如下记号. 考虑 连通的无向图 $G = \langle V, E\rangle$, 其中:
- $V$ 为需要连接的所有节点
-
$E$ 为所有可选的连通边组成的集合
\[E = \{(u, v) ~ \vert ~ w(u, v) \neq \infty\}\] - 对任何 $(u, v) \in E$, $w(u, v)$ 为连接 $u, v$ 的成本 (
Cost).
随后定义问题: 要求找到边集 $E$ 的一个 无圈子集 $T \subseteq E$ 使得 $V$ 中的所有节点均被连通, 且 涉及的边的权重之和最小:
\[w(T) = \sum_{(u, v) \in T} w(u, v)\]$T$ 是 无圈的, 且由于它要将所有节点相连, 这意味着 $T$ 是 树, 且 $G$ 为它的 扩展图 (Spanning Graph).
而 MST 问题就是: 求满足上述条件的 $T$.
2. 通用贪心算法
下面介绍一个可用于求解 MST 问题的简单算法: 通用贪心算法 (Generic Greedy Algorithm):
通用贪心算法的基本原则是: 逐步构造 MST, 每一步只取一条局部最优的边. 其伪代码如下:

我们将在讨论完该算法的正确性后解释何为 “安全的边” (Safe Edge).
通用贪心算法的循环不变量是: 在任何循环执行前, $A$ 均是某个最小生成树的组成部分.
在每一步中, 我们基于某些原则选择一条不属于 $A$ 的边 $(u, v)$, 且这条边需要满足下列条件:
- $A \cup {(u, w)} \subseteq T$.
- (u, v) 也是一条安全的边.
我们下面说明循环不变量在整个算法执行过程中都保持:
- 在初始状态下, 第 $0$ 次循环执行前显然 $A$ 满足循环不变量的条件.
- 在执行随后的任何一次循环时, 只有安全的边 (被某个
respect最小生成子树 $A$ 的分割中穿过的 权重最小 的边) 被加入进 $A$ 中构成新的部分解. - 在循环终止时, 由于已知在任意一次循环中加入到 $A$ 中的边都属于某个
MST, 因此所得到的 $A$ 必然也是一个MST.
由此, 算法的正确性得证. $\blacksquare$
下面引入 图分割 (Cut) 的概念:
定义 1.2 (图分割)
称对图 $G$ 的顶点集 $V$ 的 划分 (
Partition) $(S, V-S)$ 为一个对图 $G$ 的 分割 (Cut).
我们可以形象化地将某个对图 $G$ 的分割视为一条横贯图 $G$, 经过 $G$ 的某些边, 将图拆分成两个部分的分割线:
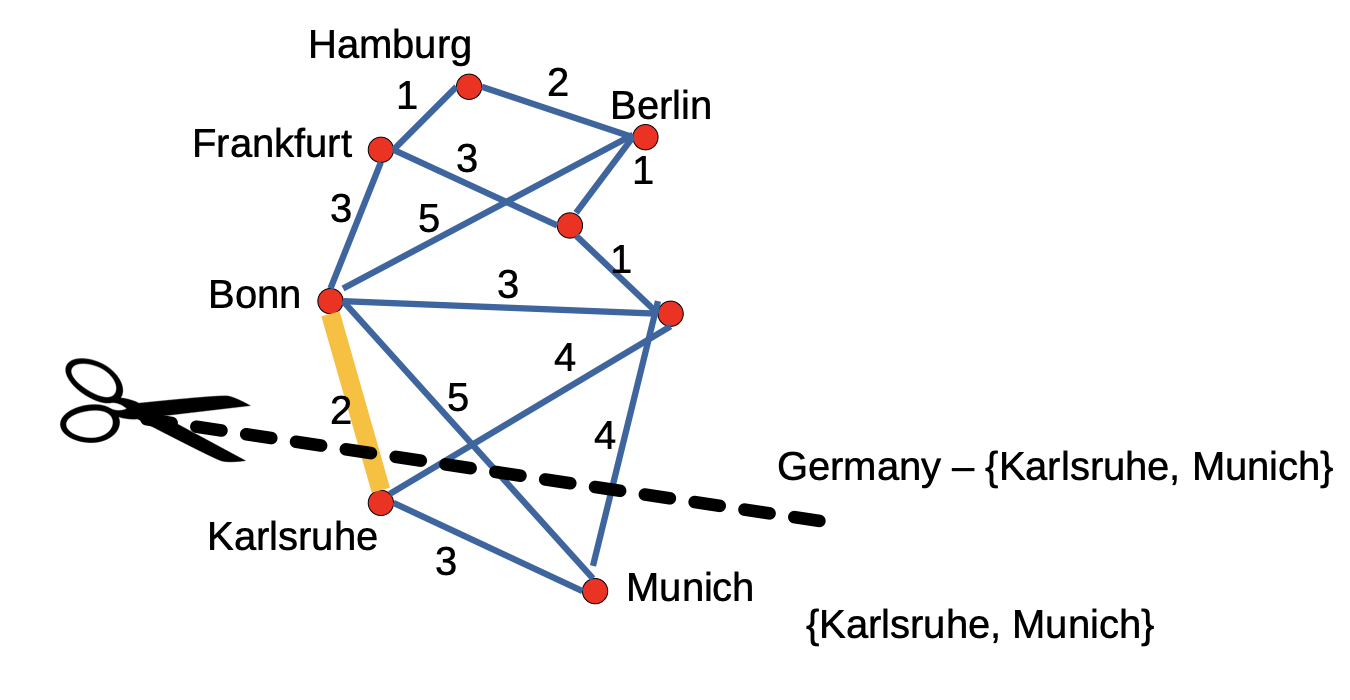
我们认为某条边 穿越了分割 (Cross the cut), 若该边的两个节点一个位于 $V-S$ 中, 另一个位于 $S$ 中.
定义 1.3 (最轻边, Light Edge)
称某条边是 最轻的, 若他属于穿越了分割的边中 权重最小的.
需要注意, 最轻边可能不是唯一的.
定义 1.4 (Respect)
称某个分割对边集 $A$ 是
Respect的, 若分割不穿越 $A$ 中的任何一条边.
最后我们定义何为 安全的边:
定义 1.5 (安全的边, Safe)
称满足下列条件的边 $(u, v)$ 是 安全 的:
- 考虑无向图 $G = \langle V, E \rangle$, 且 $E =\lbrace(u, v) ~ \vert ~ w(u, v) \neq \infty \rbrace$.
- 对图 $G$ 边集 $E$ 的子集 $A$, 它包含于某个图 $G$ 的
MST(最小生成树) 中.- 存在对图 $G$ 的分划 $(S, V-S)$, 且该分划对边集 $A$ 是
Respect的 (不穿过 $A$ 中的任何一条边).- $(u,v)$ 是被分划 $(S, V-S)$ 所穿越的边中的最轻边.
则称 $(u, v)$ 对边集 $A$ 而言是安全的.
2. Kruskal 算法
下面介绍另一个可用于寻找最小生成树的算法: Kruskal 算法.
Kruskal 算法是基于上文所介绍的通用贪心算法的扩展. 和通用贪心算法不同的是, Kruskal 算法在每一步中都会优先选择 权重最小 的边, 用权值决定在构造生成树时先后加入的边的顺序. 其伪代码如下:

需要注意, Kruskal 算法中涉及了 并查集:
-
Make-Set(x)的作用是 创建一个只包含 $x$ (自然地, 也就以 $x$ 为代表) 的 并查集: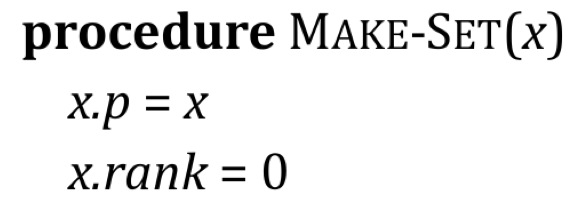
且注意此处的
x.rank指 从 $x$ 所代表的并查集中的任意子节点到 $x$ 的最长路径所包含边数的上界 (Upper bound). -
Find-Set(x)所返回的是指向存有 $x$ 的集合的表示元 (Representative):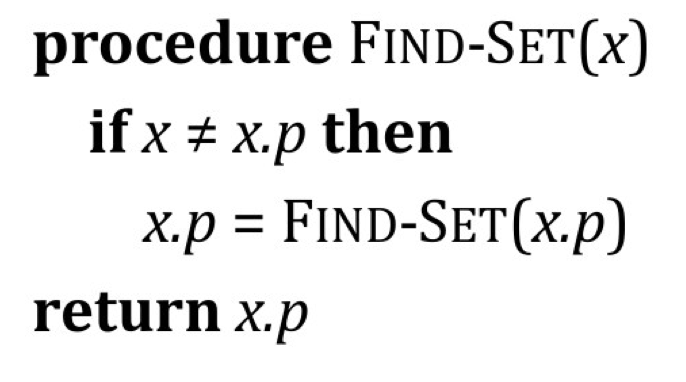
-
Union(x, y)表示将分别包含 $x$, $y$ 的两个不同的并查集合并, 合并规则为Union By Rank.
Union By Rank规则指: 在合并两个并查集时, 始终将Rank更小的那个合并到Rank更大的那个中, 且以Rank更大的并查集的代表元作为其自身的代表元.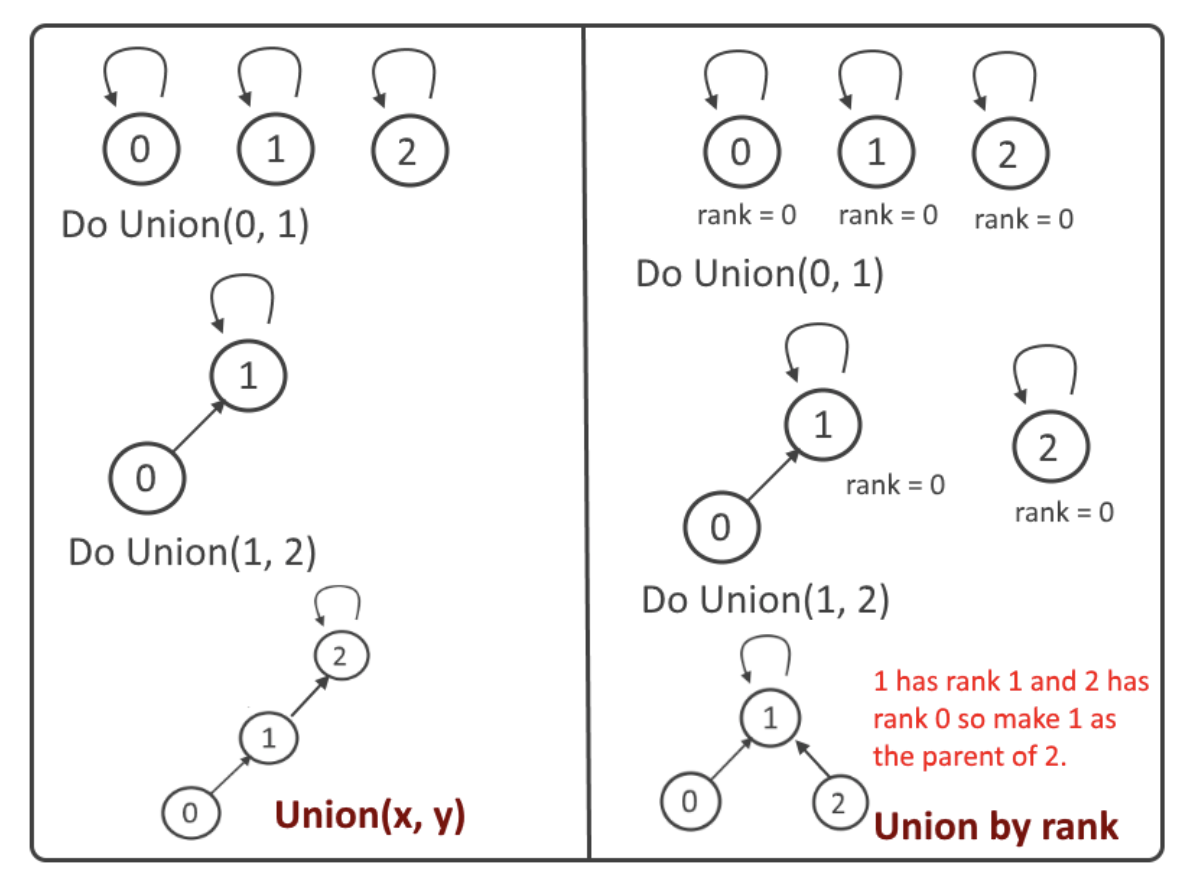
最后给出该算法时间复杂度的结论: 在 使用路径压缩 (Path Compression) 以及使用 Union-By-Rank (总是把更短的树接到更长的树上) 规则进行并查集合并的情况下, 其时间复杂度为
3. Prims 算法
下面介绍另一个最小生成树算法: Prims 算法.
Prims 算法可视为基于 Dijkstra 算法基础上的扩展. 其基本思路是:
选定任意节点 $r$ 作为要生成的最小生成树的根节点, 并循环考虑图 $G$ 的边集 $V$ 中的每个节点.
为图中的每个节点 $u$ 赋予一个 权重: 该权重表示 从 $u$ 的任意父节点连接到 $u$ 的边的权重中的最小值, 初始状态下除了选定的根节点权重设为 $0$ 外, 其余的节点权重都被初始化为 $\infty$.
随后将 $V$ 放入一个 基于权重排序的最小优先队列 $Q$ 中, 并循环检查 $Q$ 中的每个节点, 若该节点此前并不在我们的部分解 $A$ 中 (这是通过检查该点的权重判断的, 如果在部分解中的话其权值必不为 $\infty$ ), 则将该点包含到 $A$ 内, 同时更新其权值.
在 $Q$ 中再无元素时, 说明图中所有节点全部被划入解中, 且由于对节点的排序基于其权重, 我们可以确保得到的生成树的确是最小的.
Prims 算法的伪代码如下:

最后讨论 Prims 算法的时间复杂度, 显然其时间复杂度取决于最小堆的实现方式.

如果实在看不懂代码逻辑的话, 只需知道: Prims 算法和 Dijkstra 算法类似, 都是通过 “每一步加入一条权重最小的新边” 的方式从零开始构造答案的, 在每一步中, Prims 算法都会优先考虑 和当前已有的子 MST 直接相邻且权重最小的边加入 MST, 当然为了避免成环 Prims 算法考虑的边当然是最多只包含一个 A (也就是我们的子 MST) 中节点的边.
