视角
在本章中, 我们讨论计算机图形处理管线中所集成的 视角处理. 我们将先后讨论如何 建模现实中人对三维物体的观察, 并引入 “模拟人眼/相机, 在三维场景中建模 视点 (Viewing Point)” 的思路, 最后对 如何通过进行场景的变换模拟实际上不存在的相机/视点移动 进行深刻和严肃的讨论.
三维视角: 在二维视场中观察三维世界
回顾人眼在现实世界中对立体物体和场景的观察, 可以立即得知, 我们实际上所观察到的并不是真实的三维物体, 而是 三维物体的某个二维投影. 而对人类而言, 我们从肉眼接收的二维平面图形中所感知的 深度信息 是大脑通过处理视网膜传来的视觉信号 (也就是平面图片) 中 由于视角不同所产生的细微差异 而得来的. 换言之, 以二维透视的方法观察三维物体就是现实中我们观察世界的方式.

相机: 对视场的模拟
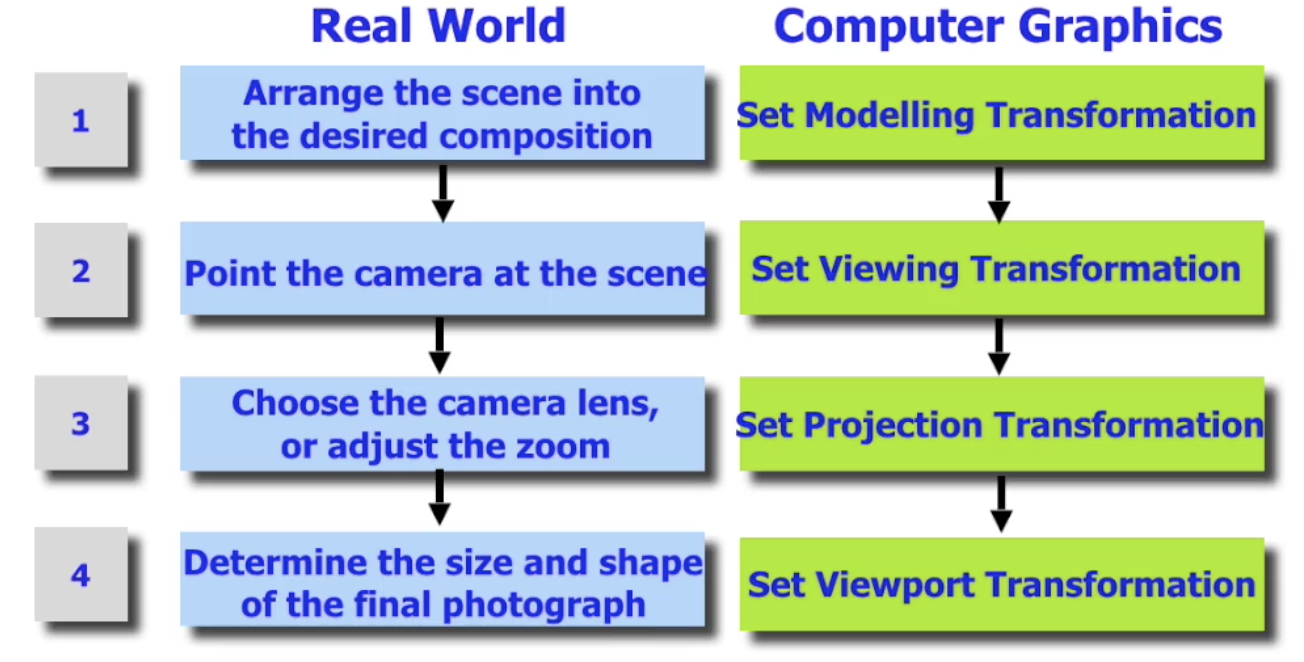
为了重现现实中人类观察世界的方式, 我们需要引入 相机 (Canera) 的概念.
现实中使用相机拍摄场景的过程大致可以分为下列四步:
- 排列和布设将要被拍摄的场景.
- 将相机放入场景中, 调整相机的指向, 使相机可以拍到我们需要拍摄的场景部分.
- 调整相机镜头 (如使用各种广角, 长焦镜头等), 实现对画面的变换. (调整光线投影到传感器上的方式)
- 最后裁切拍摄到的原始照片, 调整照片的大小.
因此, 上述四步在计算机图形学中同样需要有等价对应的步骤.
三维观察管线 (3D Viewing Pipeline)
根据上文的讨论, 我们可以得到下列的, 接收顶点坐标生成二维像素位置的 三维观察管线:
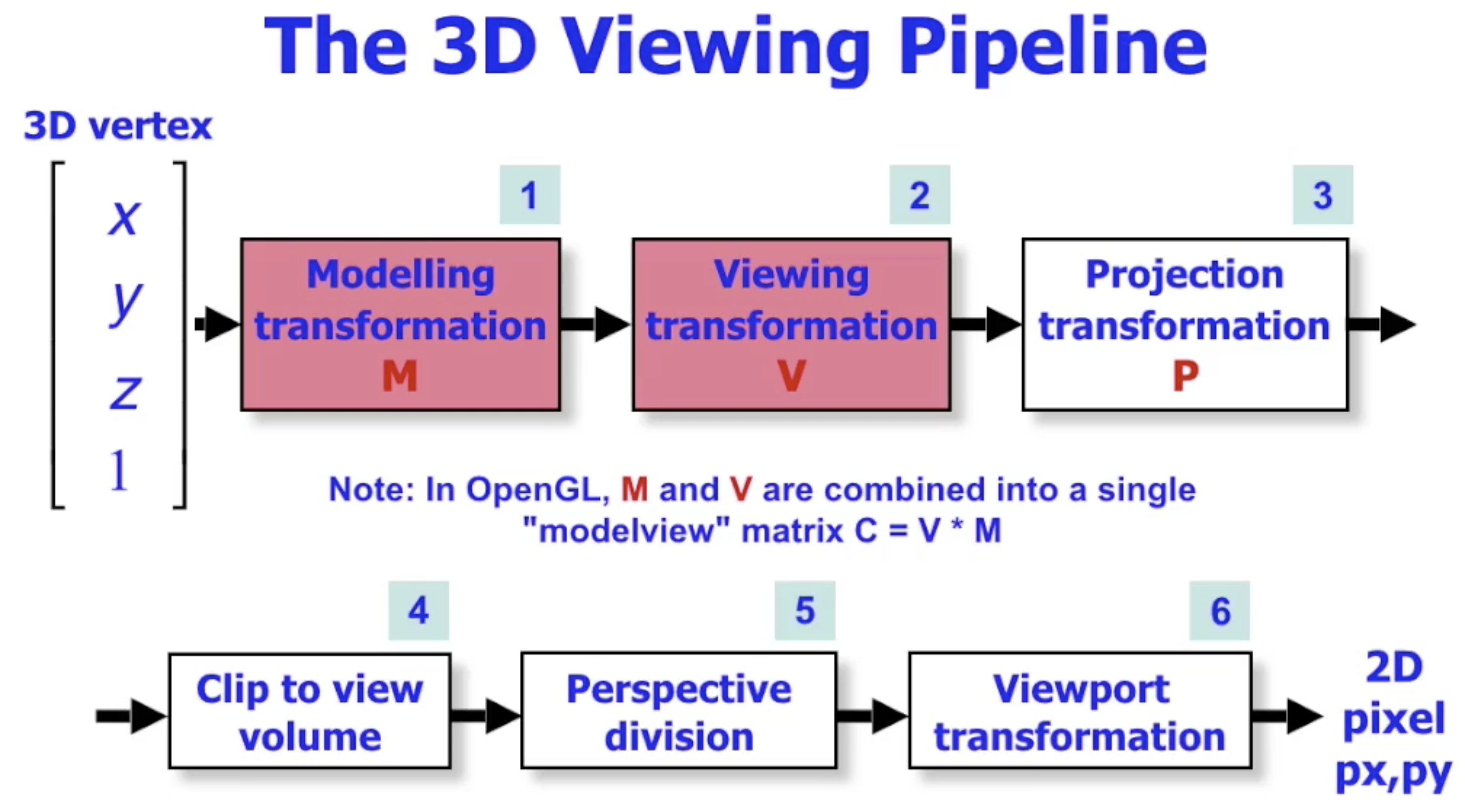
注意: 在 OpenGL 中, 模型变换矩阵和视角变换矩阵被 合二为一. 在了解了 “视角/相机实际上是被模拟出来的” 这一事实后, 我们就不难看出这种策略的合理性.
默认的观察方式
在 OpenGL 中, 默认的观察方式为: 以 $z=0$ 平面为视场 的 平行投影, 所有在三维空间中的模型上的每一个点在被观察时, 都会被 正交投影 (Orthogonal) 到 $z=0$ 平面上, 丢失全部的深度信息.
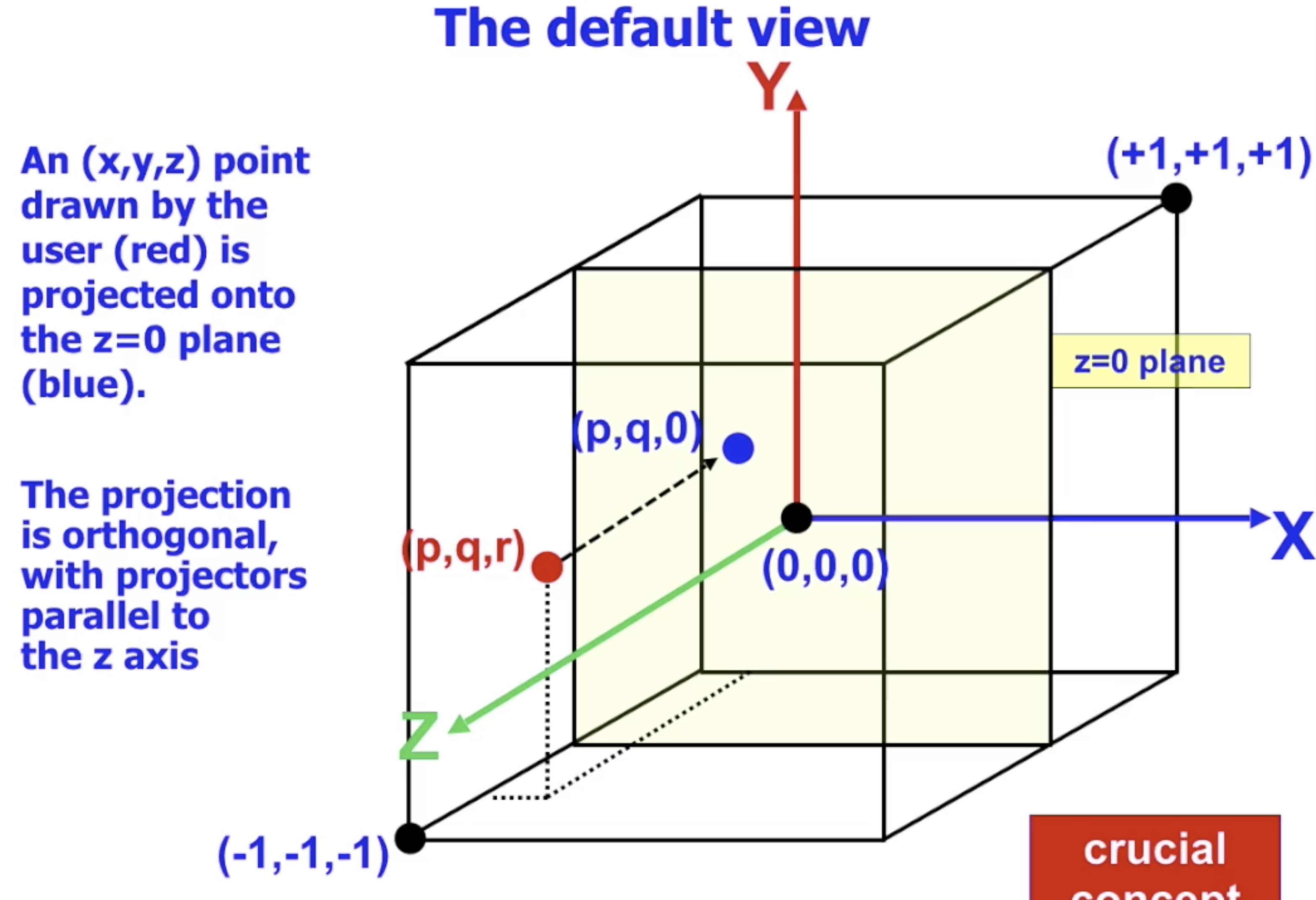
而这个 $z=0$ 平面就被 一一映射到实际的显示屏 上, 因此, $z=0$ 平面上经过正交投影得到的所有顶点和片段都直接被送入图形管线执行扫描转换, 应用 $z-buffer$ 和栅格化.
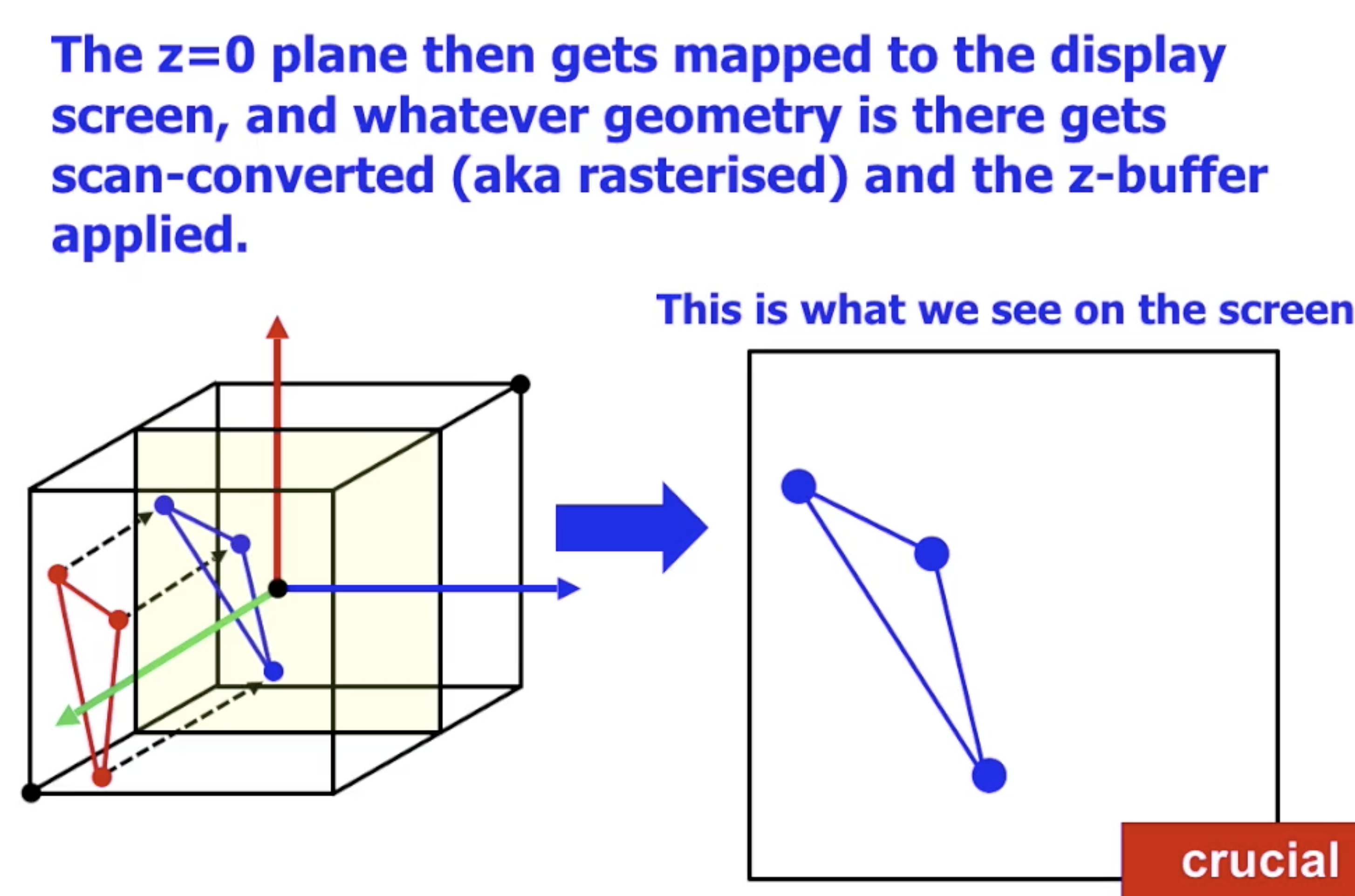
如在上图中可以看到, 位于立体空间中的红色三角形经过正交投影后在 $z=0$ 平面上得到了蓝色的三角形, 它将直接作为原始数据经过图形管线处理后变成实际被显示的内容.
计算机图形中的相机: 模型变换和视角变换的二元性
考虑在三维空间内使用 相机 观察场景, 则可知通过调整相机的位置/角度, 我们可以得到不同的场景图片. 而相应地, 由于场景和相机之间发生的是 相对的位置和角度变换, 因此反过来, 如果 用相反的方式 对 整个场景 的位置和角度进行变换, 我们也能得到完全一致的图像.

这意味着, 我们实际上可以 在计算中忽略相机这一实体的存在, 只将它的 概念 保留, 通过 变换场景 间接实现 变换其实不存在的相机 的效果.


计算相机坐标系
为了模拟相机的存在, 我们仍需要定义一个 纯粹概念上的 相机坐标系.
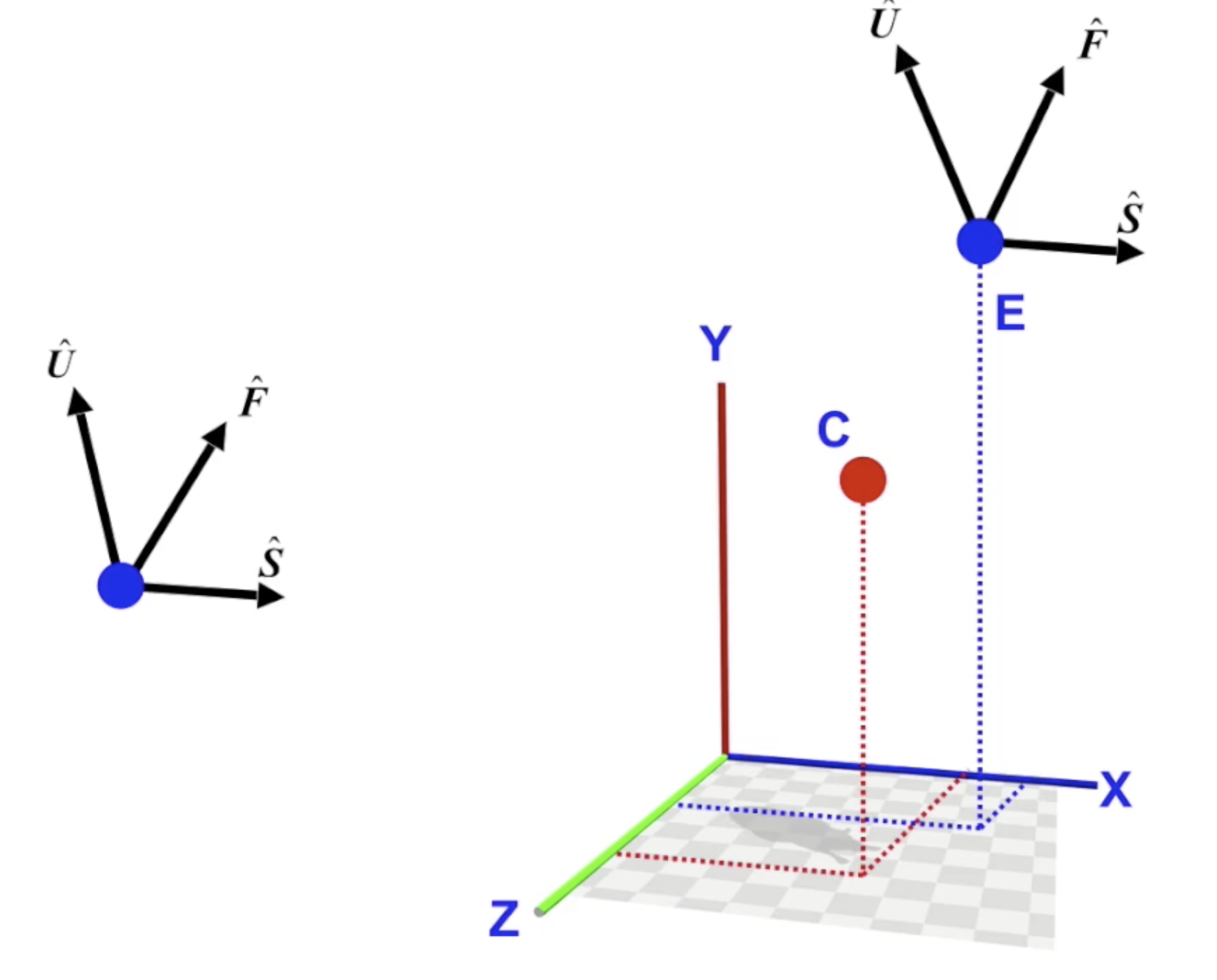
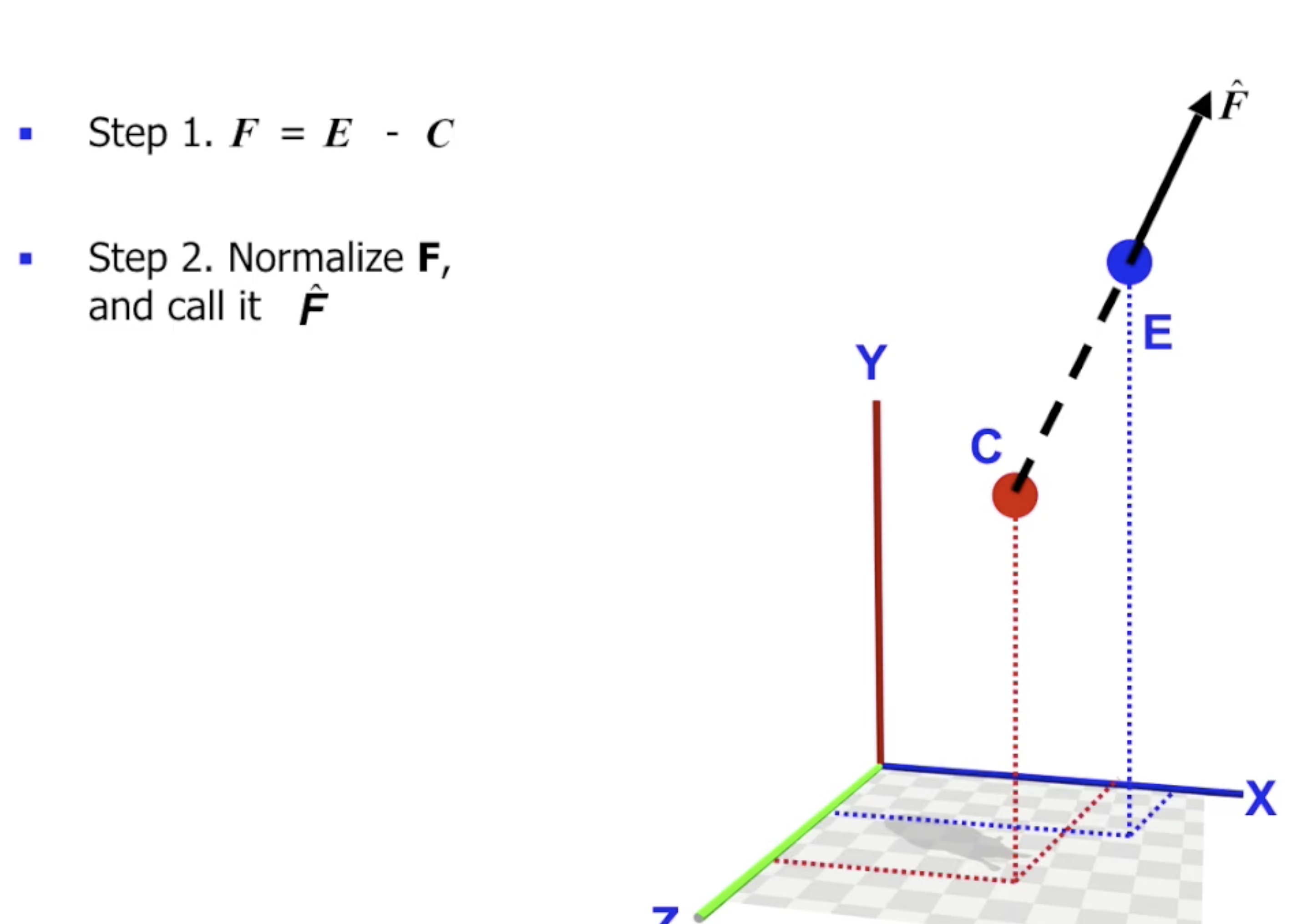
分别记相机坐标系中的三个坐标轴为 $U, F, S$. 其中 $F$ 为 从被观测物体到相机位置的向量的规范化 (向量模长为 $1$).
而第二步, 我们需要定义 相机朝上的方向 $U$. 我们本可使用相机自身的 “朝上的向量 $V$”, 但 $V$ 不一定和 $F$ 垂直, 因此需要 对 $V$ 进行分解 从而得到 $U$.
幸运的是, 我们知道向量叉乘 $F\times V$ 的结果恰和 $F-V$ 平面垂直, 因此我们直接将叉乘 $F \times V$ 后得到的向量规范化, 作为相机坐标系的 $S$ 坐标轴方向.
最后, 将 $S \times F$ 规范化, 就得到了 $V$ 垂直于 $F$ 方向上的单位分解, 这就是所需要的 $U$.
由此, 给定 从物体到相机的向量 和 表示相机大致向上方向的向量 $V$, 我们可用上述步骤计算出相机坐标系中的三个方向坐标轴的单位向量.

计算视角变换
我们最后讨论如何从 实际上不存在的相机要执行的视角变换 计算出 整个场景需要执行的等价变换.
由于实际的视点 位于坐标原点, 因此要执行任何视角变换, 就首先需要构造出 将概念中的相机视点及其坐标系 转换到 坐标原点和三维空间坐标系 上:
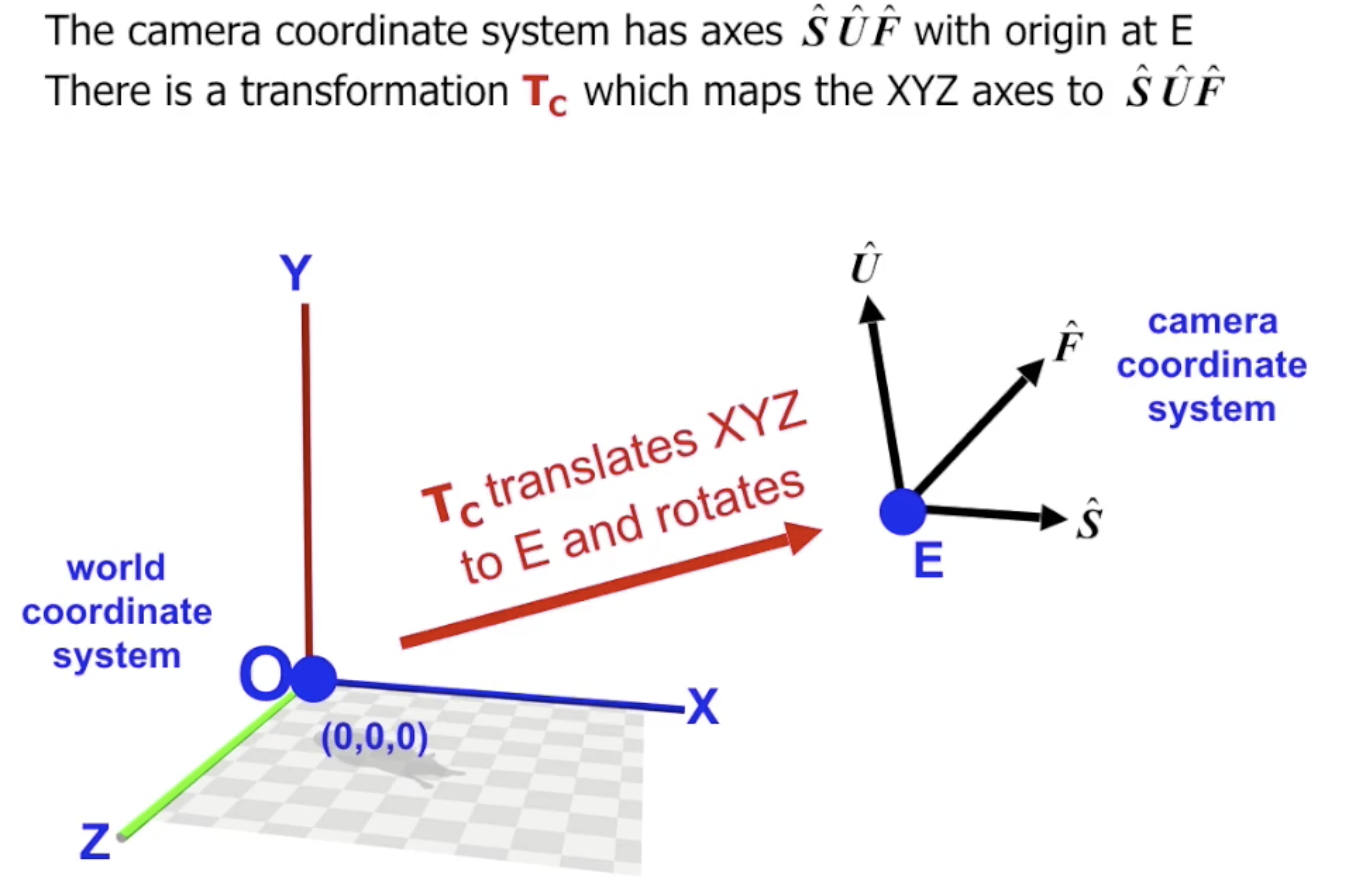
记从 场景坐标系 到 相机坐标系 的转换为 $T_c$, 则将被应用到物体上的转换就是 它的逆: $T_{c}^{-1}$.
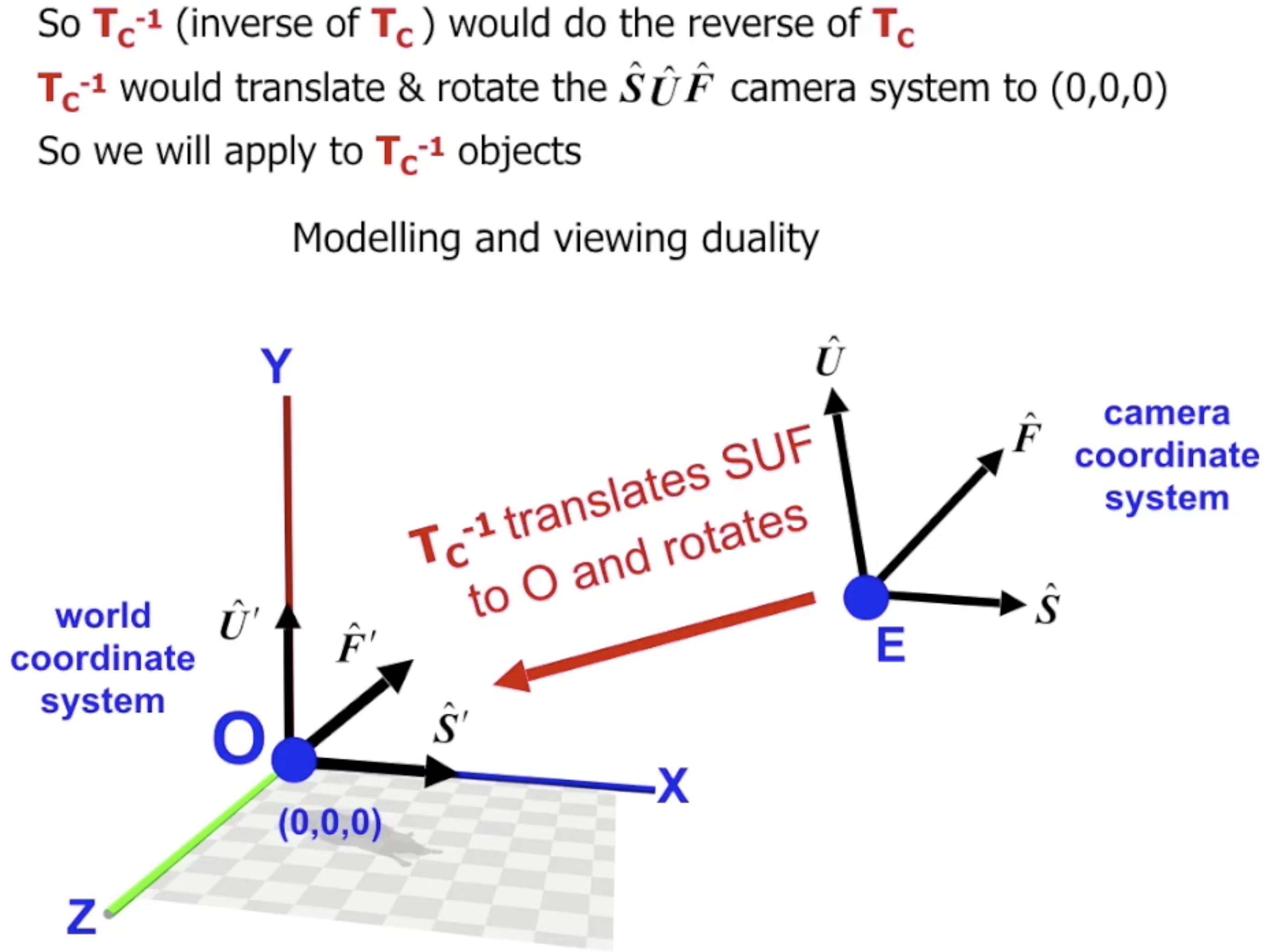
下面讨论它的计算方法. 计算 $T_{c}^{-1}$ 分为两步: 计算平移变换 $T_1$ 和 计算旋转变换 $T_2$. 由于使用齐次坐标, 这样的变换不难推导:
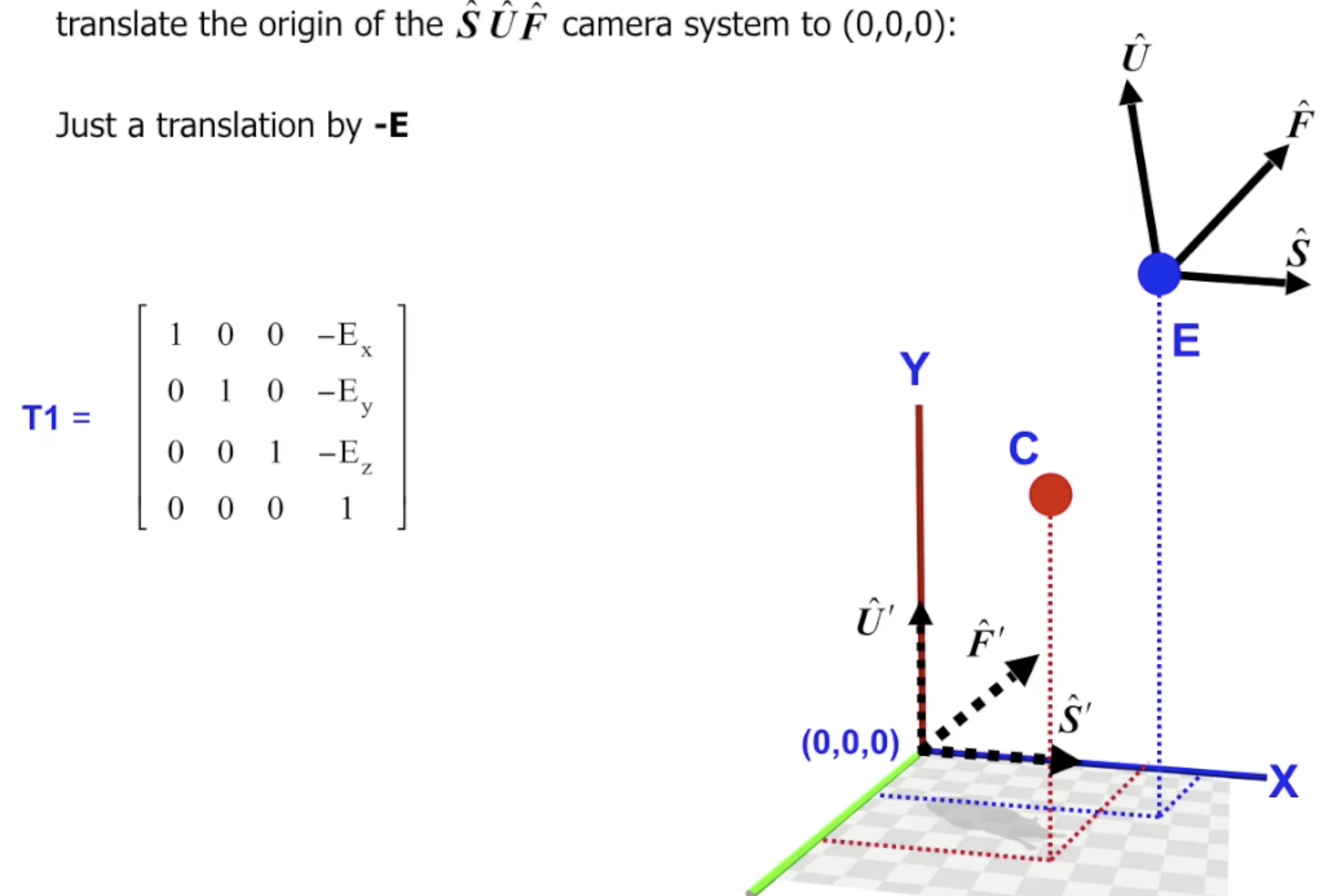
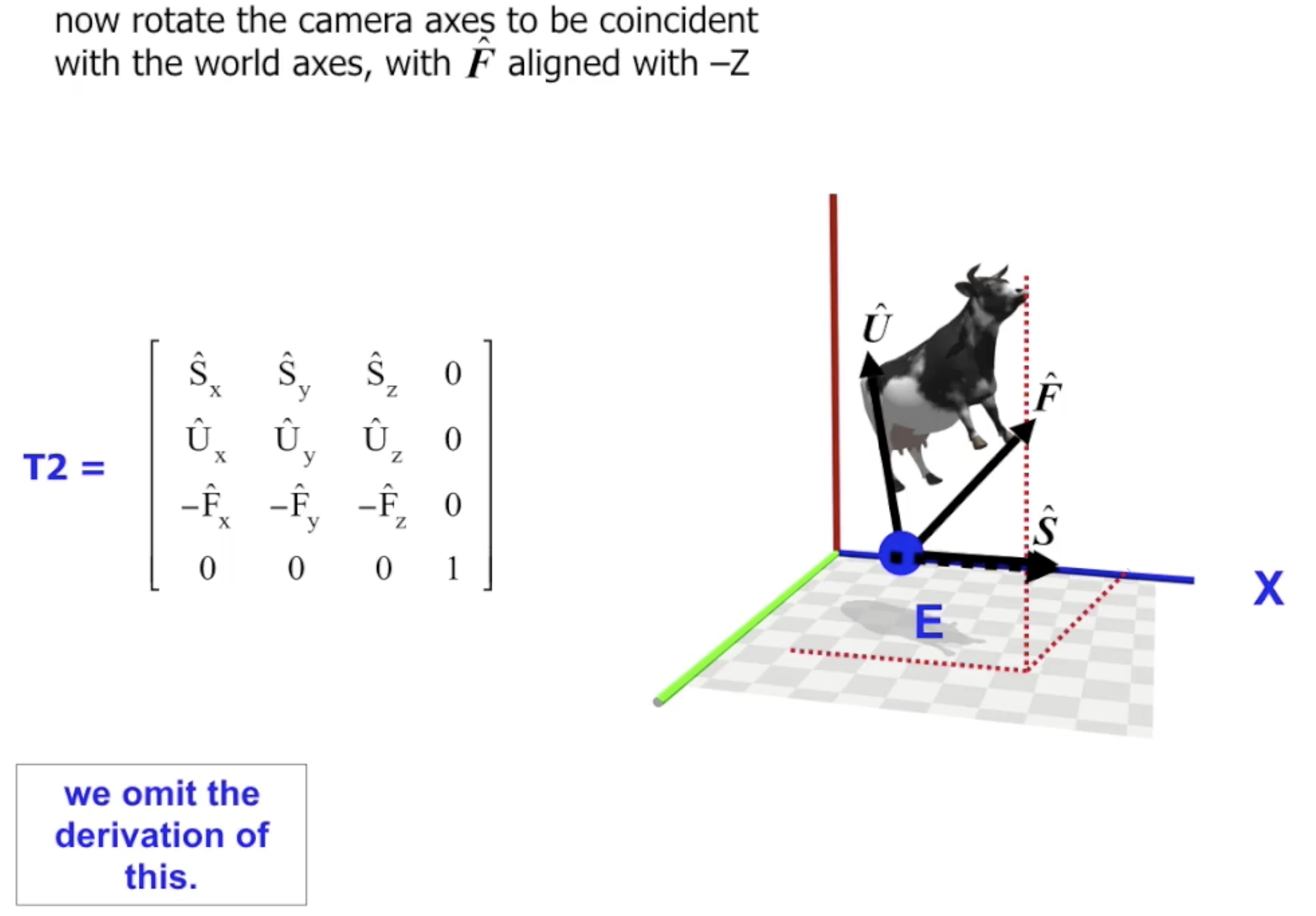
最后将 $T_1, T_2$ 合成就得到了 $T_{c}^{-1} = T_2 \cdot T_1$.
总结
最后将视角变换原理和规则总结如下:

所谓 “没有相机” 的意义在于: 在三维空间中不存在可以自由移动的相机, 我们将实际上固定在坐标原点的视点直接视为相机, 所有的 “视角” 变换实际上都是 三维空间中的所有物体相对坐标原点的变换.
在 ThreeJS 中, 相机的默认位置在原点, 观察方向朝着 $Z$ 轴正方向.
而它同时封装了视角转换, 因此我们可以使用 camera.lookAt(x, y, z) 方法进行 概念上的 相机视角变换, 无需关注内在的实现细节.

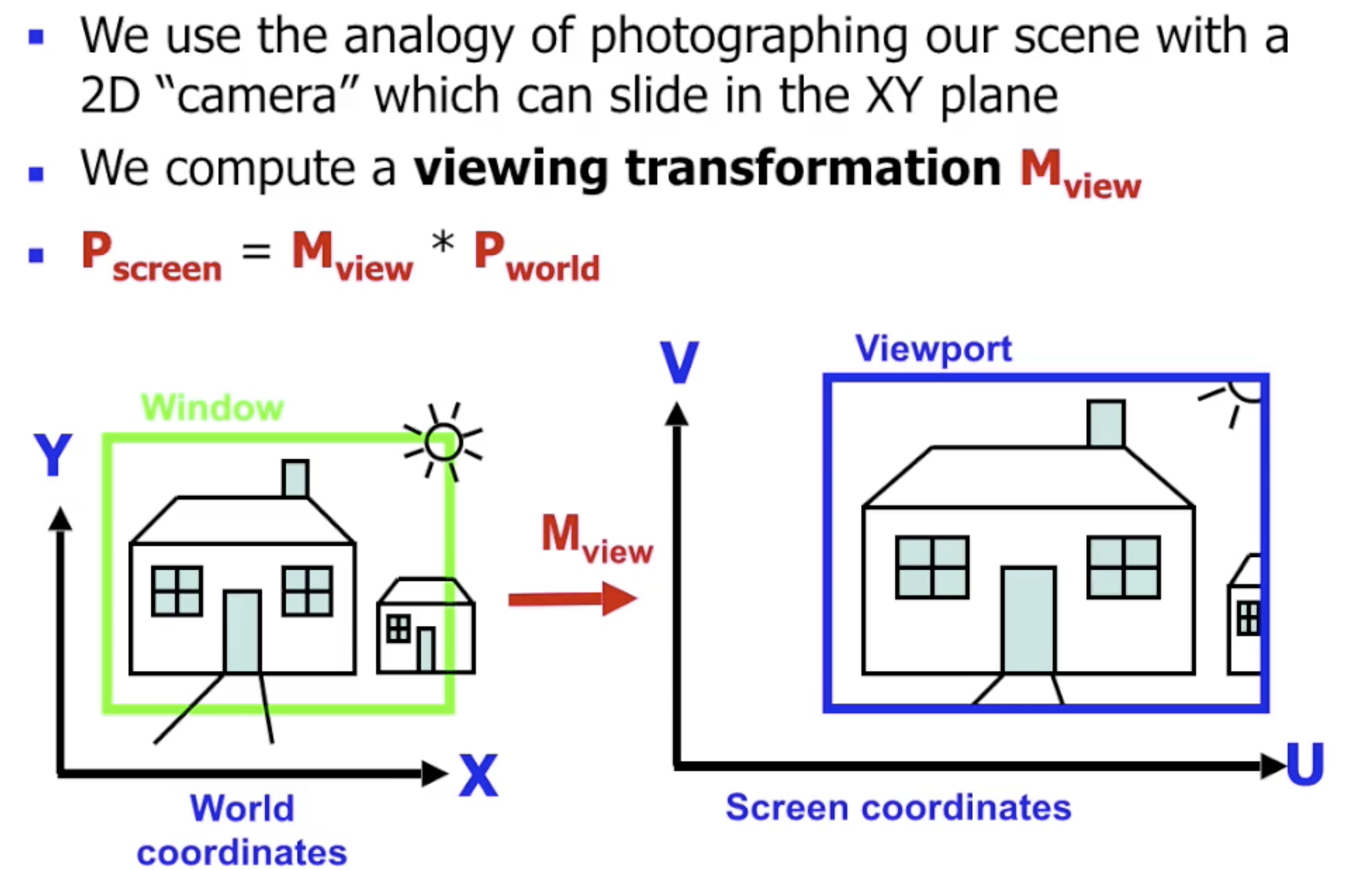
二维视角: 使用视窗过滤二维世界
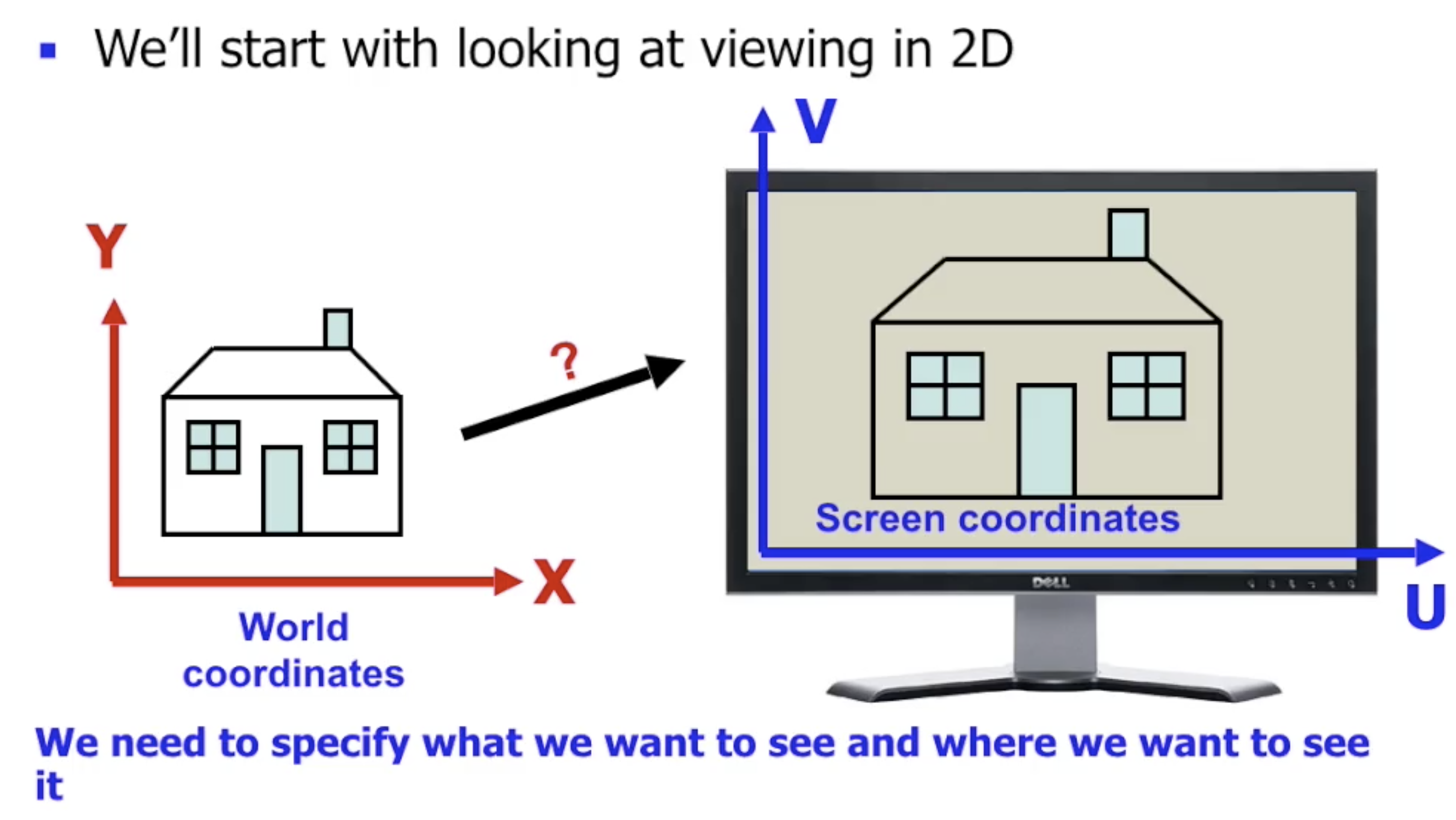
我们下面讨论在二维平面内的视角.
和三维视角情况下, 将三维世界空间映射到二维的屏幕平面一样, 二维视角中的问题是如何将二维的世界空间映射到屏幕上.
但是, 此处我们只需要明确 我们希望观察的物体是什么 以及 希望观察到的范围.
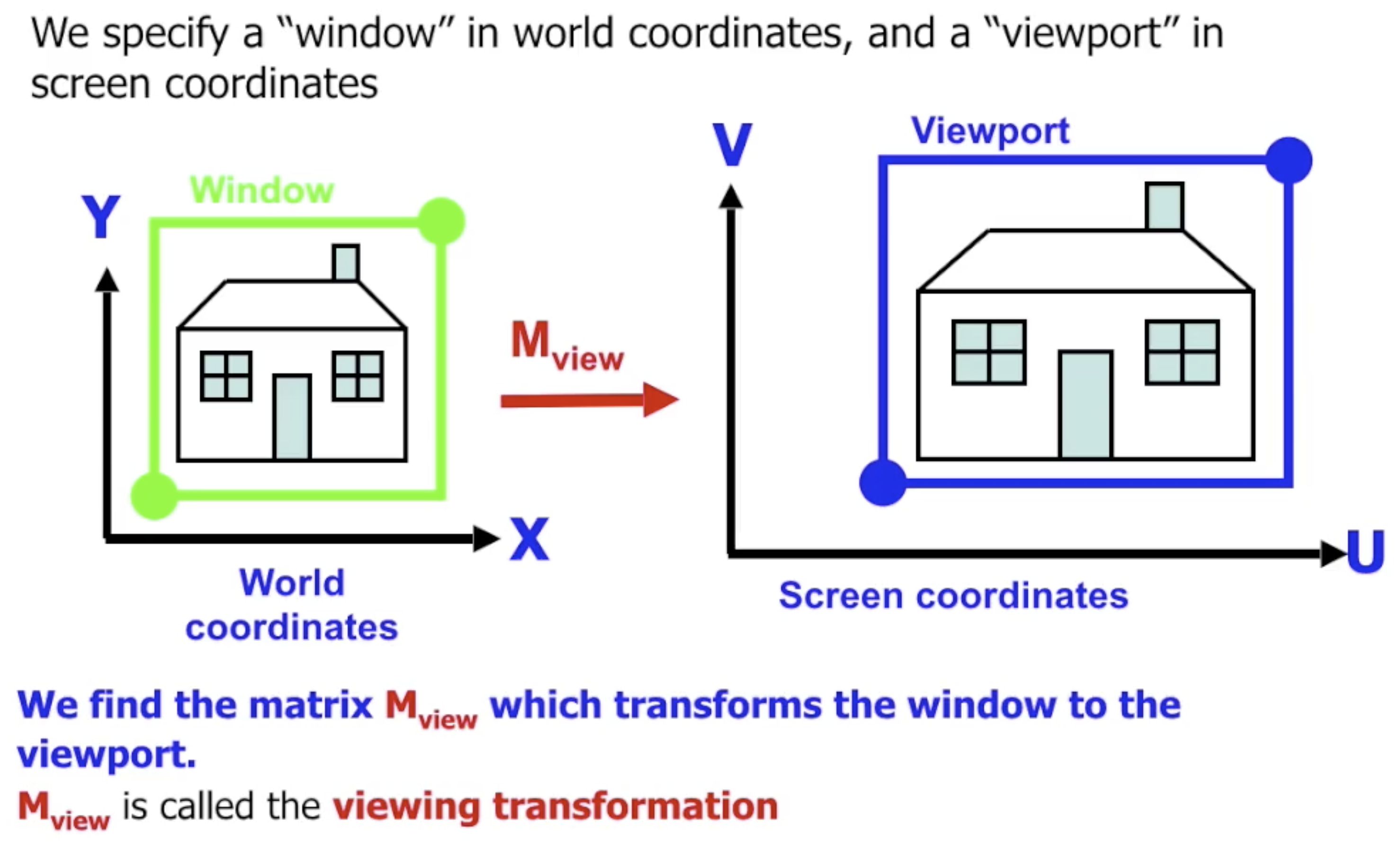
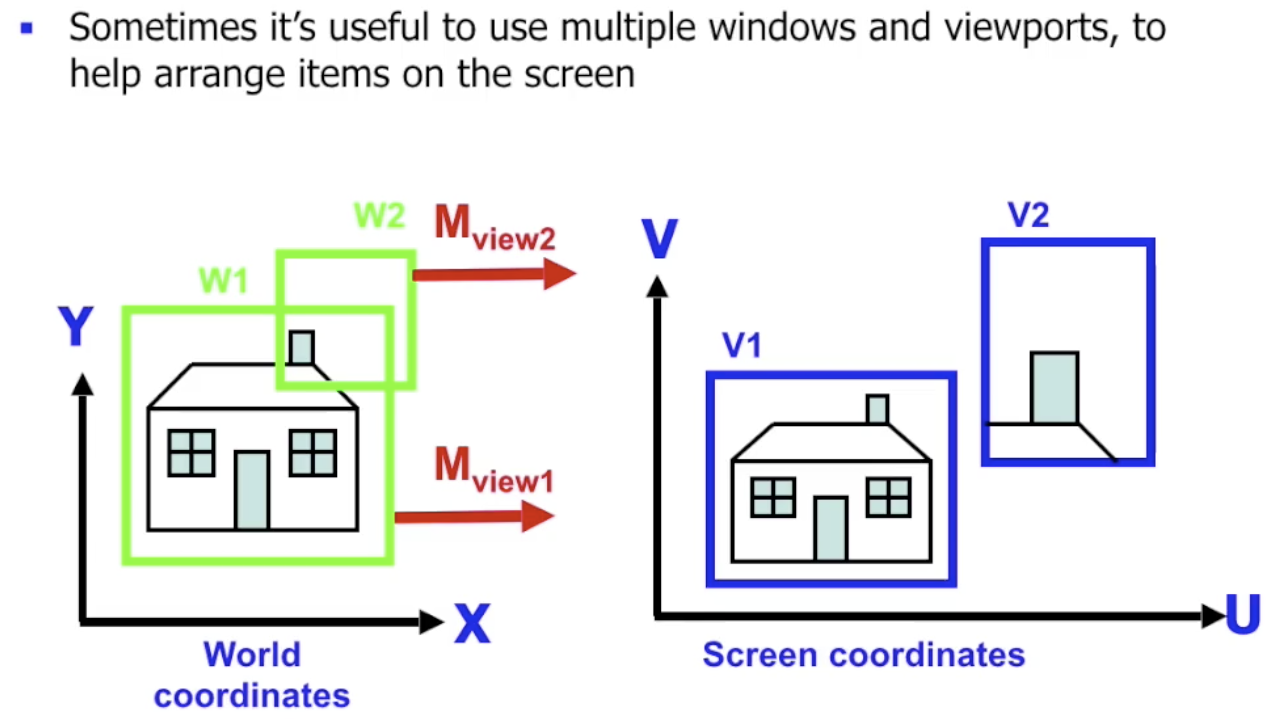
视窗
在考虑三维视场时, 我们使用 相机 的概念对视角变换进行建模. 而在二维视场中, 我们使用 视窗 (Window) 描述我们所期望在二维世界中的观察范围, 它将被映射在屏幕上对应的 观察口 (Viewport) 中.
视窗 标定了 我们对世界的观察范围, 相当于对 原始二维世界的裁切, 因此仍然需要使用转换矩阵 $M_{\text{view}}$ 将视窗映射到屏幕上的 “观察口” 中.
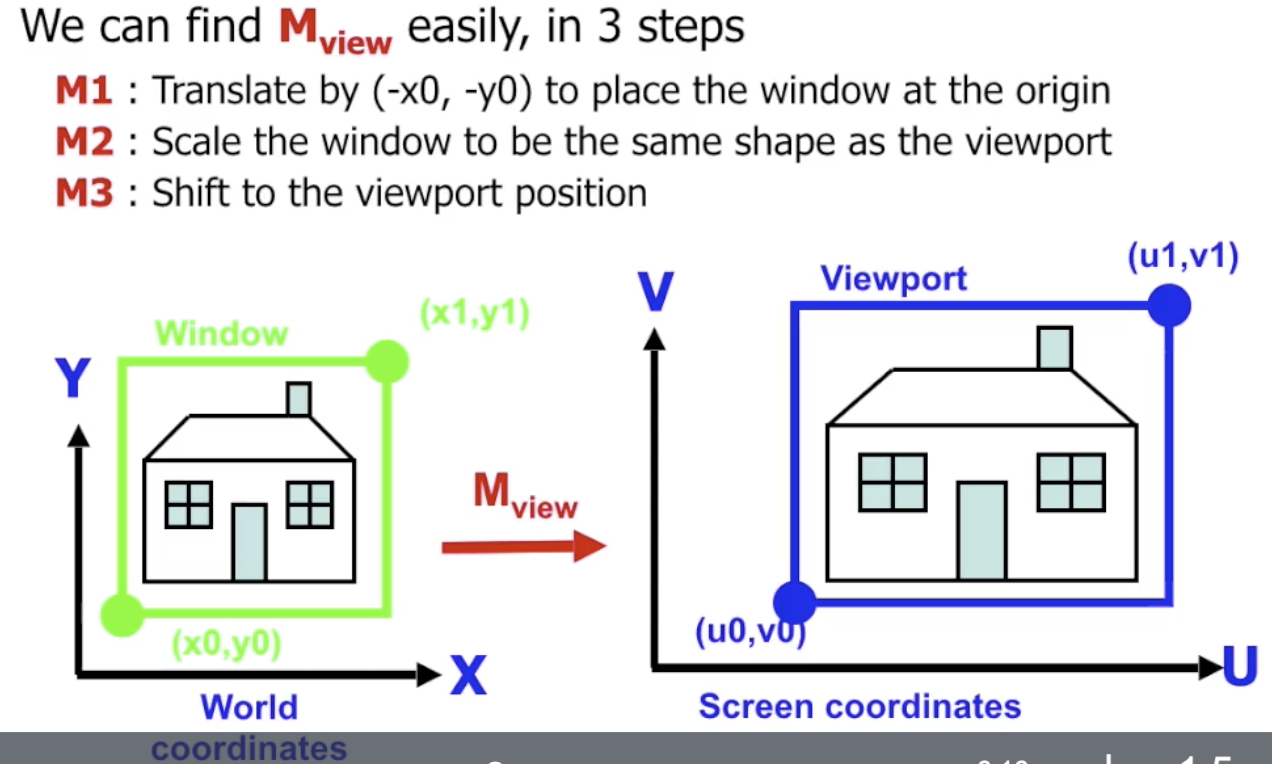
转换矩阵的构造也极其简单, 因为它本质上 就是对视窗的拉伸. 回顾拉伸矩阵的生成过程:
- 平移视窗左下角到坐标原点, 便于下一步执行拉伸变换.
- 执行拉伸变换.
- 将拉伸过后尺寸和观察口一致的视窗平移到观察口的位置上.

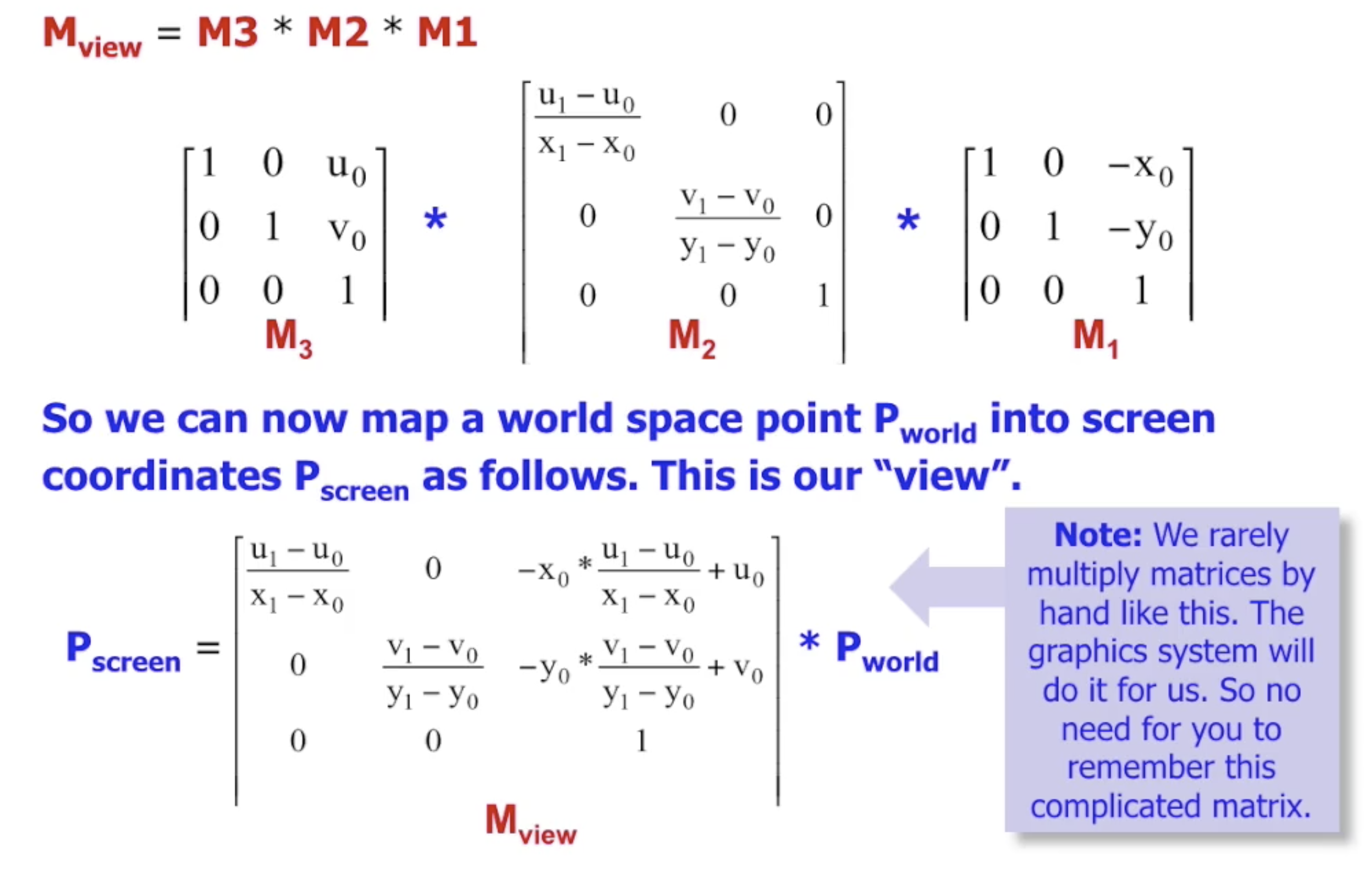
裁切和多视窗
一般地, 视窗的大小都 小于实际图形, 因此还需要对二维世界中的图像进行 裁切.
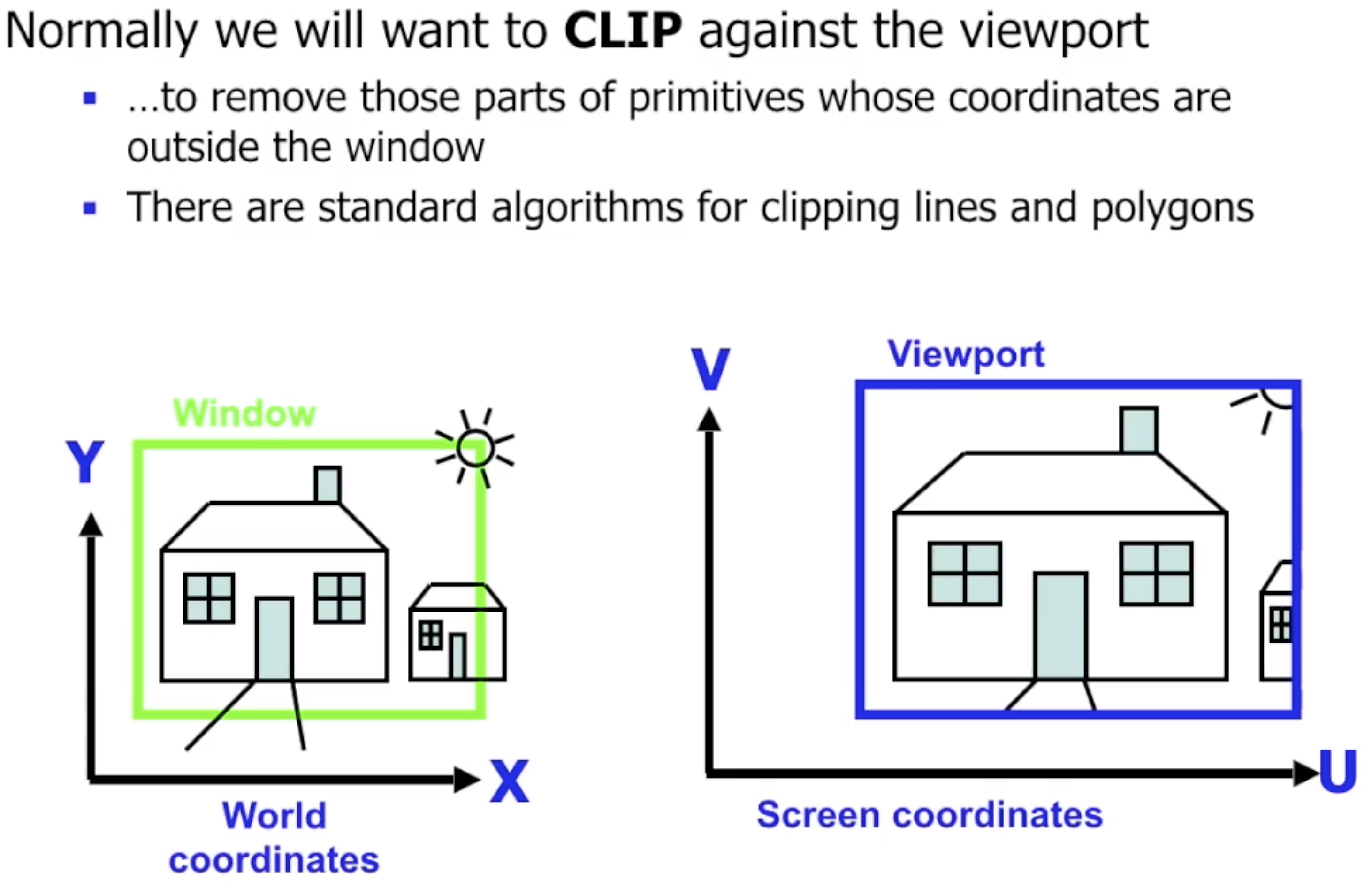
并且一般地我们还会同时使用多个视窗, 它们对应实际屏幕上的多个 ”观察口“, 而且可能重叠.
最后对二维平面中的视角变换总结如下: