启发式图算法: Dijkstra 和 A*
本章继续讨论最短路径问题, 并引入两个用于计算图最短路径的重要启发式算法: Dijkstra 算法 和 A* 算法.
1. Dijkstra 算法
在上一章中, 我们已经知道可以使用 Bellman-Ford 算法以 $O(\vert V\vert \vert E \vert)$ 的时间复杂度解决有权图 $G = \langle V, E\rangle$ 上的最短路径问题.
由于 Bellman-Ford 算法的时间复杂度与图的边数和节点数均相关, 随着问题涉及的图逐渐复杂化, 再用 Bellman-Ford 算法解决最短路径问题会不再可行. 因此, 我们下面介绍效率更高的 Dijkstra 算法:
1. 原理

Dijkstra 算法利用了 “单源最短路径的子路径仍然是最短路径” 的性质, 使用贪心的思想逐步构建局部最优的最短子路径:
上图伪代码中的 D 就是依据节点权重排序的 优先队列, 确保在 while 循环中总是优先检查路径权重更小的点, $F \cup D$ 中的每个点都一定是能够从起始节点 $s$ 访问到的, 因此不可达的点将不会被检查到, 算法的效率得到提高.
需要注意, 和 Bellman-Ford 算法不同的是, 前者 只是不能应用在存在权重为负的圈的图中, 而 Dijkstra 和 A* 算法都不能应用在存在负权边的图中, 这是因为两者都基于贪心原则选择局部最优点构造部分解, 而 负权边的存在会破坏局部最优性, 如:
 同时注意, 在这里
同时注意, 在这里 Dijkstra 算法的 initEstimate() 逻辑和 Bellman-Ford 算法是 一致的: 只有起始节点的目标路径权重初始估计为 $0$, 其余任何节点的估计都是 $\infty$.
2. 实现
Dijkstra 算法需要一个优先队列用于存储已发现但待检查的点. 由于我们关心路径权重估计更小的点, 因此在此处一般使用 最小堆 实现优先队列.
而在任何优先队列操作 (如插入/弹出)以及执行了对特定节点的松弛操作后, 都需要维护堆序性质.
此外, 由于 Dijkstra 所考虑的任何节点都一定是能够通过起始节点 $s$ 访问到的, 因此该算法在执行过程中不会考虑也不会存储任何不可达点 (Unreachable) 的信息, 进而无需在优先队列中存储任何以 $\infty$ 为预估权重的点. (定义不可达的点权重为 $\infty$)
3. 性质
由于算法从初始节点出发逐步向外扩展, 因此:
- 每条边最多被松弛一次.
- 任何节点最多被插入进优先队列一次, 同样地也只会被从中删除一次, 没有多余操作.
同时, 由于我们使用 最小堆 实现优先队列, 因此 插入, 提取/弹出, 对给定边的松弛 操作的时间复杂度均为 $O(\log{\vert V\vert}).$
最后, 结合上述的两点性质可知, 由于在整个操作中任何边最多被执行一次松弛操作, 任何节点最多被插入优先队列一次, 弹出优先队列一次, 因此算法整体的时间复杂度为
\[O((\vert E \vert + \vert V \vert) \cdot \log(\vert V \vert)).\]2. A* 算法
下面考虑一个基于 Dijkstra 算法基础上的改进: A* 算法.
1. 原理
Dijkstra 算法仍然存在的问题是: 虽然它无需再如 Bellman-Ford 算法一般, 不用再去考虑任何不可达点, 但它仍然需要对所有的可达点遍历一遍才能得出结果. A* 算法在其基础上使用启发式方法对搜索空间进一步进行剪枝, 从而获得了更高的执行效率.

2. 差异
A* 算法的启发式与 Dijkstra 的差异在:
-
后者完全基于 权重 评价生成的部分解的优劣, 前者的评价标准综合了 部分解当前的尾节点到起始节点的距离 (也就是权重) 与 尾节点到目标节点的距离, 从而具有指向性: 权重越小, 距离目标节点越近的部分解越有可能被选定从而构造完整解.
\[\text{heuristic(u)} = D(u) + \text{distance}(u, \text{target\_node})\] -
由于对可选部分解排序方式的转变, 最终完整解一旦在某一步中进入我们的选择范围内, 就一定会因为启发值最小而被优先选择, 从而剩下的所有较差解都不会再被考虑, 达到了剪枝的效果 (如
Lab5中优化的BNB).
3. 启发性
下面简单介绍 某个启发函数能够被用于优化算法 的条件: 可启发性 (Admissibilty) 和 启发单调性 (Monotonicity).
定义 2.1 (可启发性)
启发式函数的作用是对算法生成的部分解进行估计, 判断它距离完整解还有多少差异或距离.
称启发式函数的 可启发性 为: 在任何情况下启发函数 $h(u)$ 返回的估计都 不能超过从这个部分解出发达成目标所需要花费的真实代价 $\delta(u, t)$:
\[h(u) \leqslant \delta(u, t)\]
定义 2.2 (启发单调性)
启发式函数还需具备 单调性 才能更好地用于优化算法 (注意,
\[h(a) \leqslant w(a, b) + h(b).\]A*算法中的启发函数即使不满足单调性仍然可用).
启发单调性指, 在任意给定的当前解 $a$ 的基础上扩展任一步 $b$ 后, 启发函数 $h(a)$ 均满足:也就是所谓的 “三角形不等关系” (
Triangle Inequality):
3. Dijkstra 和 A* 算法的正确性
我们在本章的最后一节讨论两种启发式算法的正确性.
1. Dijkstra 算法的正确性
Dijkstra 算法的不变量是:
-
对于任何位于 ”已完成检查集合“ $F$ 中的点 $u$, 从起始节点到该点最短路径的权重估计一定都是精确的:
\[D(u) = \delta(u).\] -
对任何在某个位于 $F$ 中的点 $u$ 之后插入原来的路径的点 $v$, 从起始节点到 $v$ 的最短路径的权重估计 $D(v)$ 有下列的上界:
\[\forall v, ~ D(v) \leqslant \delta(u) + w(u, v).\] -
对起始节点到边集 $V$ 中任何点的最短路径的权重估计都是 过高的估计:
\[\forall u \in V. ~ D(u) \geqslant \delta(u).\]
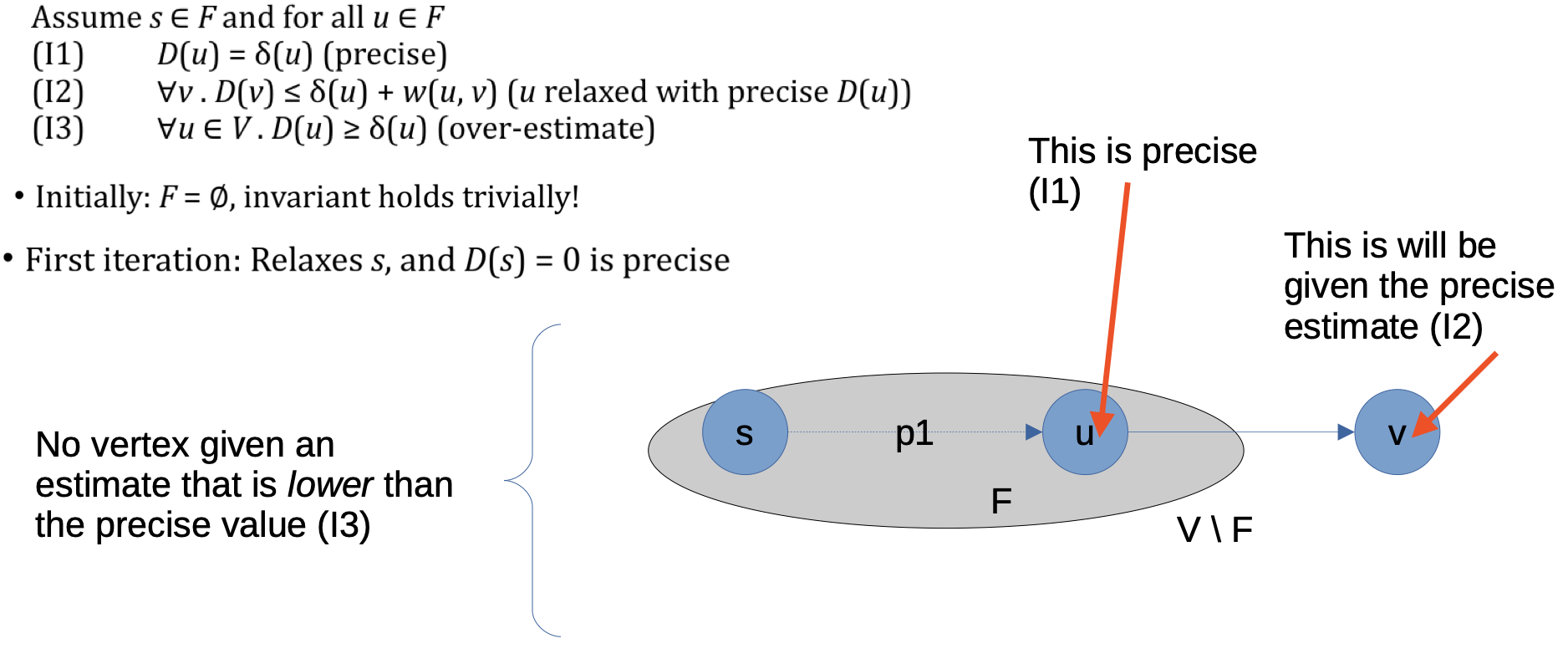
显然在第 $0$ 次循环时, 有 $F = \emptyset$, 不变量在初始状态成立.
在第 $1$ 次循环时算法首先将起始节点 $s$ 松弛, 因此 $D(s) = 0$, 同样满足不变量.
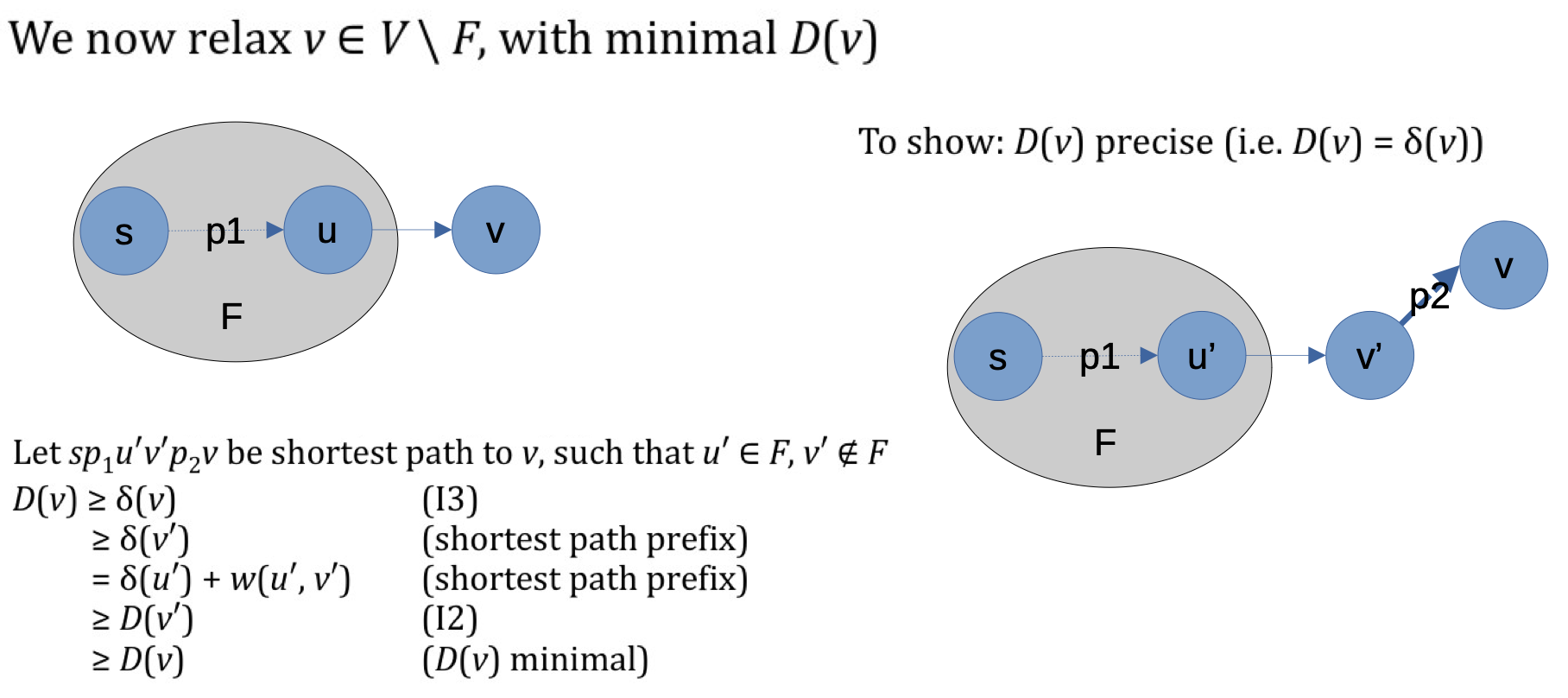
下面考虑一般情况:
2. A* 算法的正确性