渲染多边形
多边形和像素
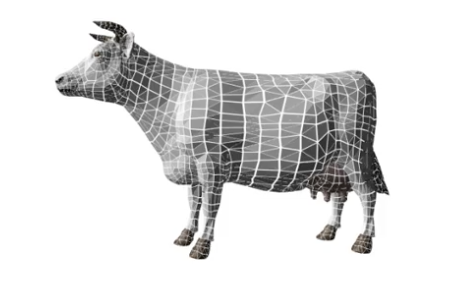
多边形是 计算机图形渲染中的基本单位之一. 虽然可行的渲染方式 不唯一, 基于多边形的渲染由于具备高度的通用性且便于存储, 表示和渲染三维图形, 因此被广泛应用. 如下图所示, 我们可以使用多边形组合出复杂的图形, 模型或场景.
基本定义: 多边形, 曲面细分 (Tessellation),
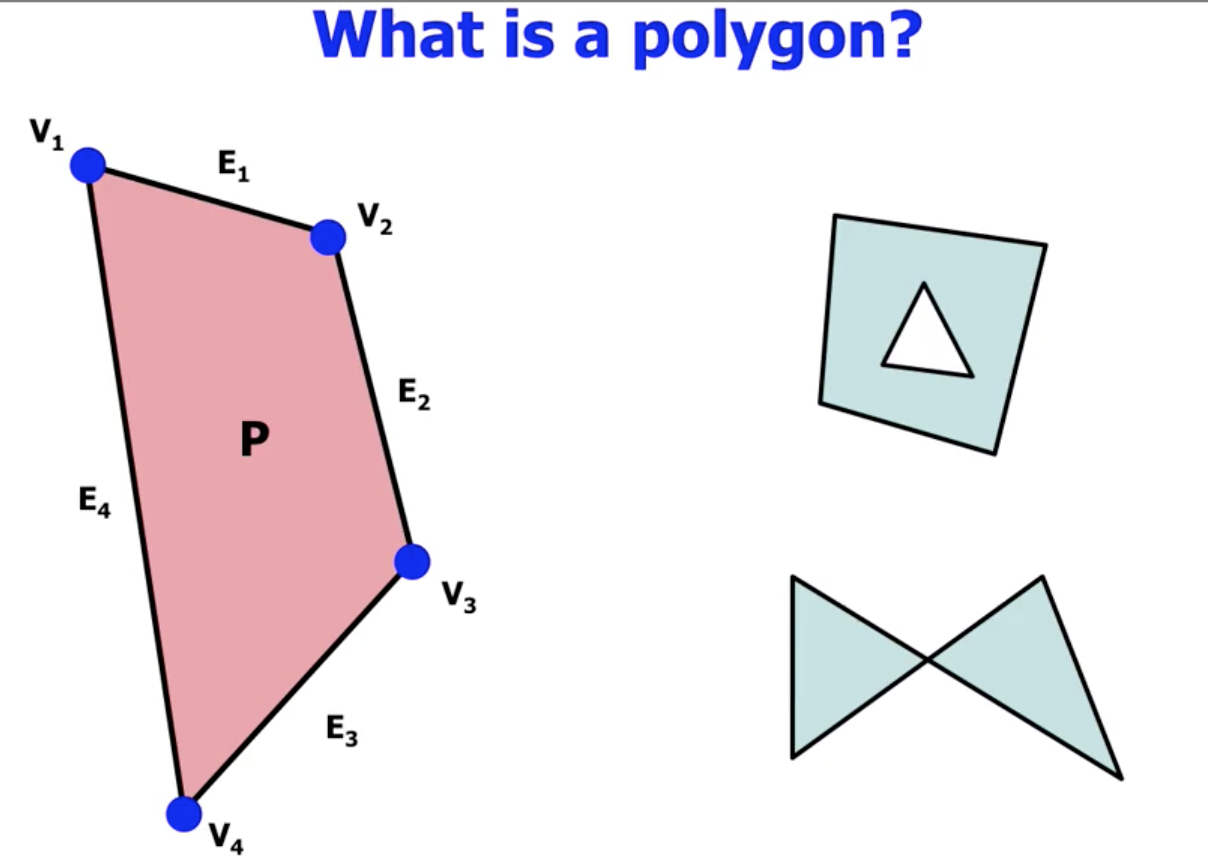
首先回顾 多边形的定义. 我们知道, 由 三条或以上 的线段 首尾顺次连接 组成的 平面图形 被称为 多边形, 它可被 一系列顶点和边 所表示.
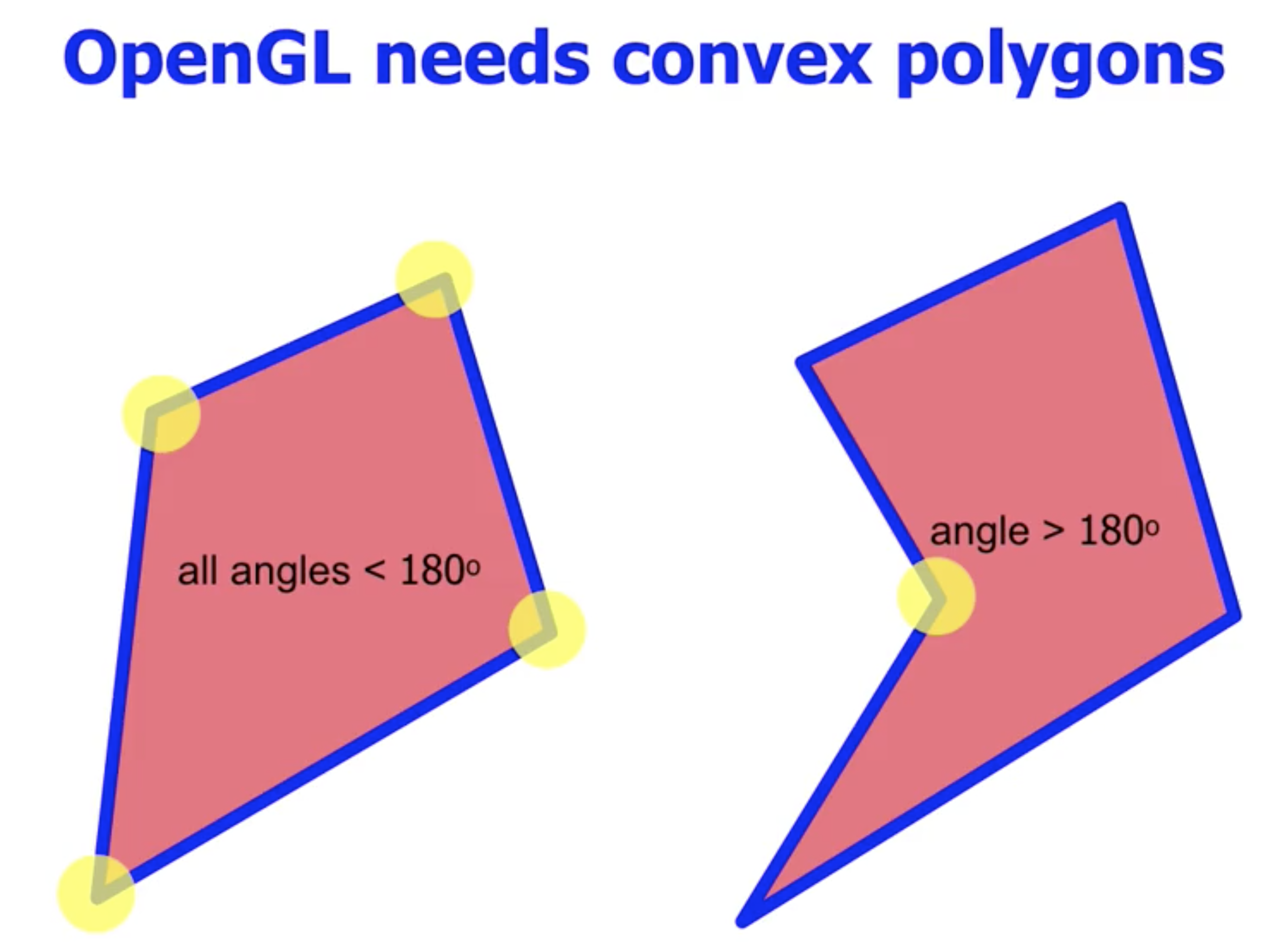
OpenGL 使用 凸多边形 (Convex Polygon), 也就是 所有顶点外角均大于 $180 \degree$ 的多边形. 若遇到 凹多边形 (Concave Polygon), 则 OpenGL 无法直接正确地渲染它们, 因此需要先将它们转换为凸多边形.
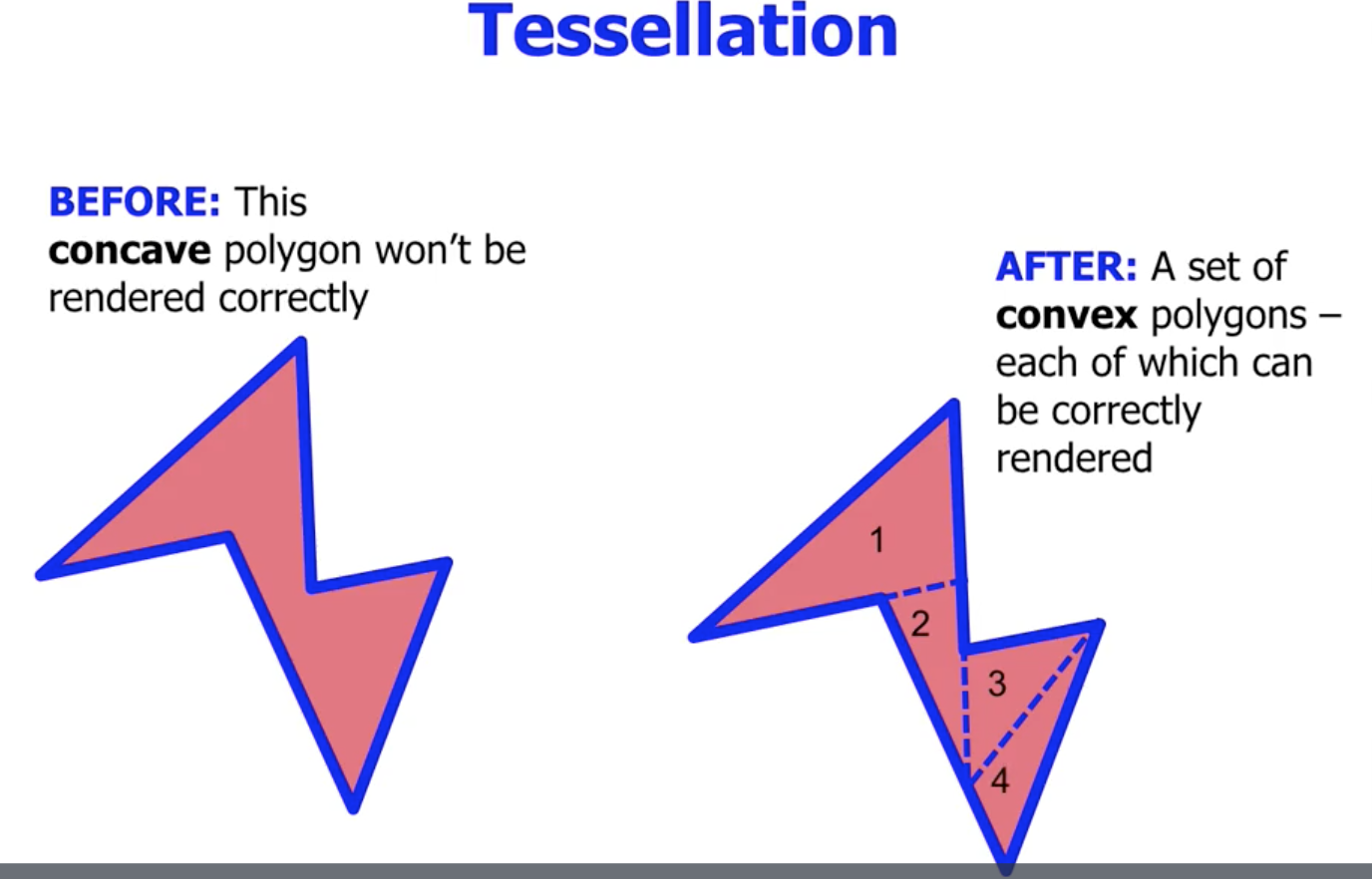
曲面细分 (Tessellation). 就是 将凹多边形裁切为多个凸多边形 的技术. 通过将凹多边形裁切为 多个相邻凸多边形的拼接, OpenGL 就可以曲线救国的方式通过渲染这些凸多边形实现等价的凹多边形渲染.
曲面法线 (Surface Normal) 的定义和计算
多边形的另一个重要性质是 曲面法线, 它的实质是 垂直于多边形所在平面的射线, 因此得名 曲面法线. 曲面法线可以用来 定义多边形所在平面 的 前面和后面, 进一步就可表示多边形的 方向 (Orientation), 这在 计算光照, 多边形剔除 (Culling) 以及 碰撞检测 中大有作用.

回顾 向量叉乘 的定义可知, 在三维平面中两条 起始点相同且不共线 的向量叉乘的结果 恰为垂直于这两条向量所在平面的法线, 因此计算法线的方式实际上就是:
- 找到多边形中的 任意一对依次相连的边向量. 由于多边形任意内角均不为平角, 只要两条边相连, 他们的边向量就是不共线的.
- 由于这一对向量中其中一条 (记为 $E_1$) 的终止点是另一条 (记为 $E_2$) 的起始点, 因此对 $E_1$ 取反得到一对 起始点相同 的向量 $(-E_1, E_2)$.
- 计算 $(-E_1, E_2)$ 的叉乘 $N = E_2 \times -E_1$, 结果 $N$ 的 单位向量 就是该多边形的曲面法线, 曲面法线的方向可以用 叉乘的右手定则 判断, 所以下面图中的曲面法线其实方向反了()

注意:
- 在计算叉乘时, 永远是 没有被取反的向量在前乘以另一条被取反的向量!
- 最后一步对叉乘结果取单位向量的过程就是 标准化 (
Normalization).
多边形浓汤 Polygon Soup
回顾本章开头的那头用多边形表示的牛, 它可以视为由 $18000$ 个多边形表示的三维模型. 由于在模型中 绝大多数的多边形都是相邻的, 也就是说它们 共用一些边和节点, 因此如果我们存储每一个多边形, 就重复存储了大量冗余信息. 显然这存在巨大的空间浪费.
因此我们称通过存储 该模型中每一个多边形 来保存模型的方式为 Polygon Soup. 模型中大量的冗余信息正如冒着泡的粘稠浓汤, 这一比喻活灵活现, 言简意赅, 不过笔者认为, 也许 “多边形脓汤” 这个比喻更加的生动形象.
多边形浓汤表示法 (Polygon Soup) 的主要问题是空间浪费, 除此以外我们还不难看出它由于不存在任何层级信息, 因此彻底丢失了模型中的语意信息, 我们再不能分辨给定的多边形究竟保存的是 (举例而言) 牛的哪个部分, 或是某个房屋中的哪个房间等. 进一步地, 它也使得与模型的交互变得同样困难.

使用网格表示三维模型
使用 网格 (Mesh) 表示模型可以克服多边形浓汤表示法的这些缺陷. 还是以上面的三维牛模型为例, 它在网格表示下所需要存储的顶点数量只是原来的 $\frac{1}{3}$.
网格存储法通过将多边形表示为按照某种规则相连共用部分节点和边的网格化结构来降低存储开销. 常用的网格化结构是 条状的Triangle Strip 和 形如扇形的 Triangle Fan.
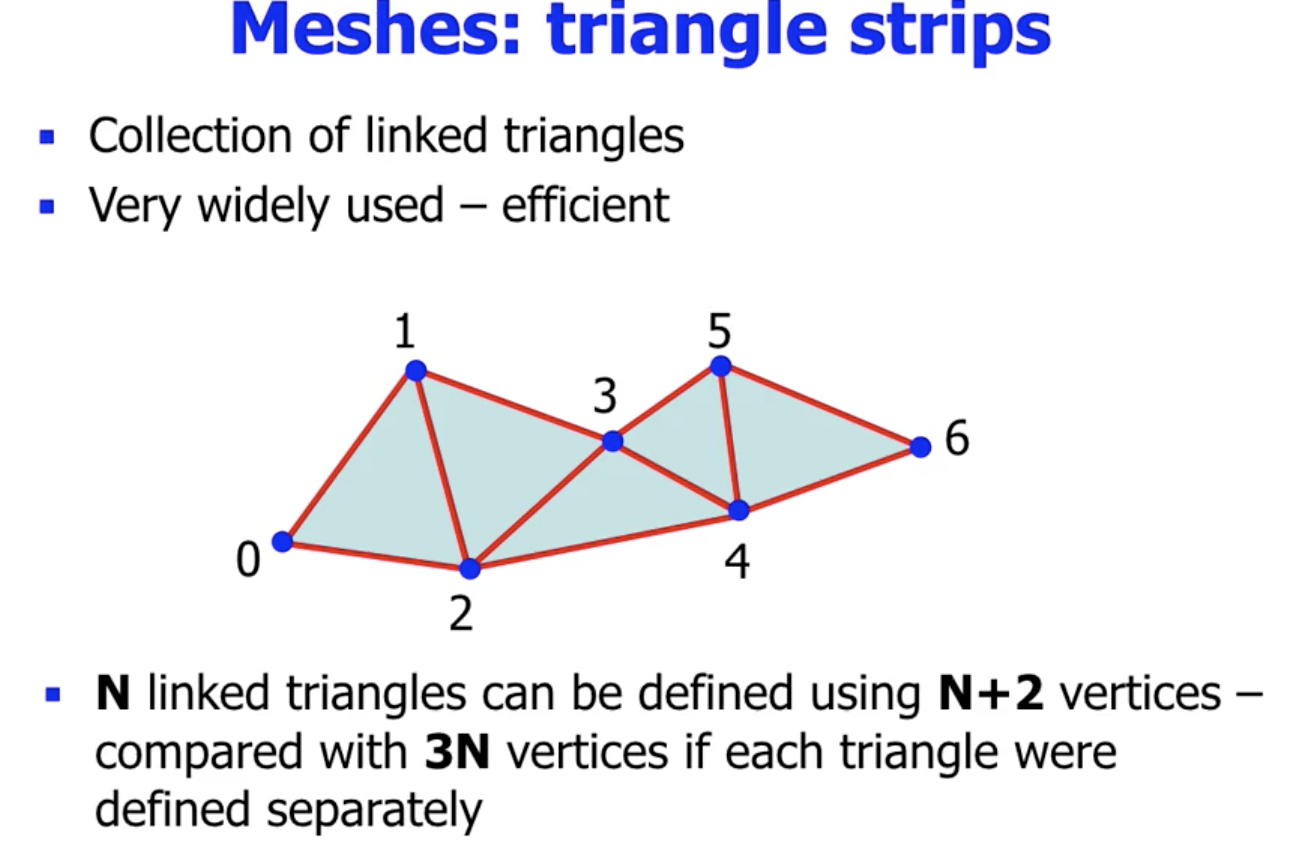
Triangle Strip
该结构认定 三角形之间通过某条共用边相连, 形成的网格呈 条带形. 对 $N$ 个相连的三角形而言, 只需要存储 $N+2$ 个顶点, 存储效率很高 被广泛应用.
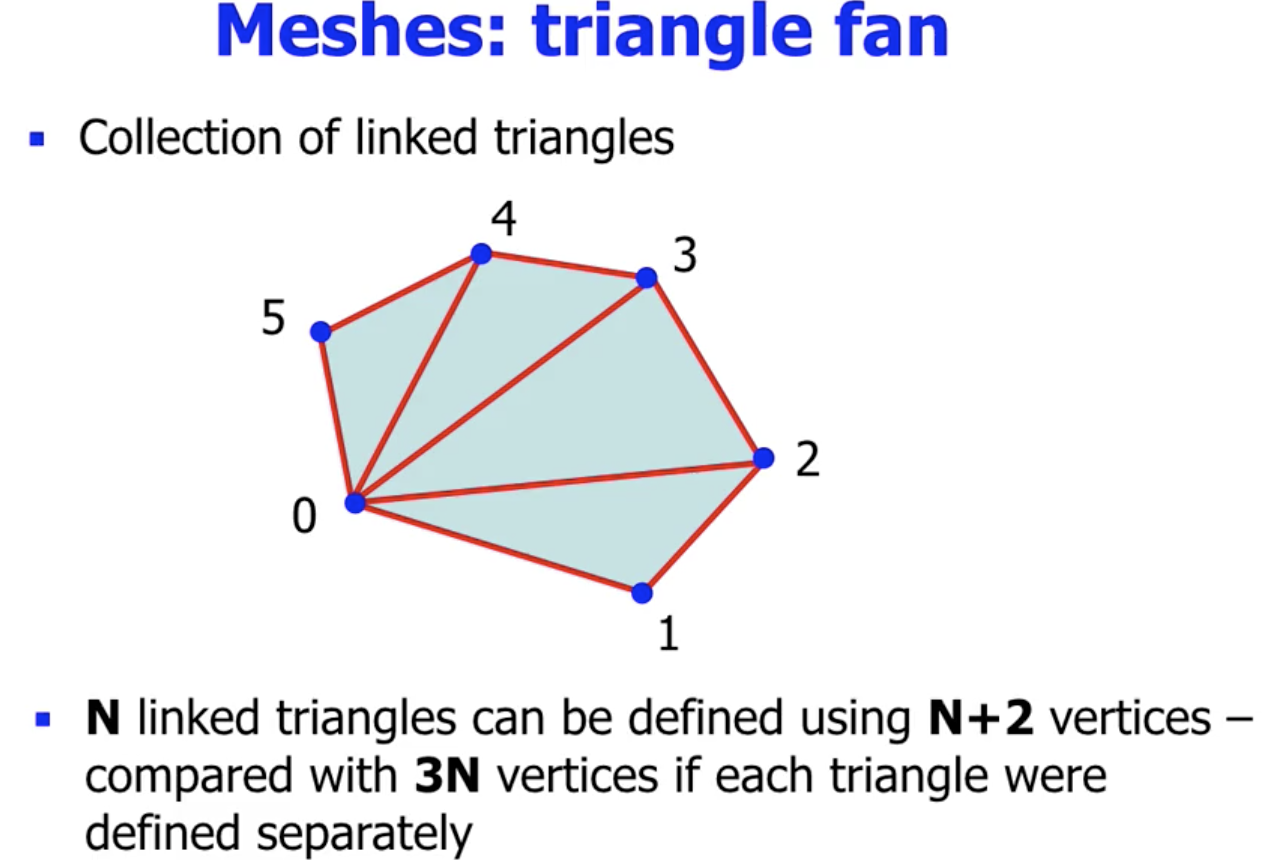
Triangle Fan
另一种结构的假设是, 所有三角形共用一个顶点. 如此形成的就是一个 扇形结构. 其空间复杂度和 Triangle Strip 完全一致.
Quadrilateral Strips
在从 “基于三角形的网格表示” 逻辑中解放思想后, 我们立刻发现考虑依次相连的正方形也可以表示曲面:
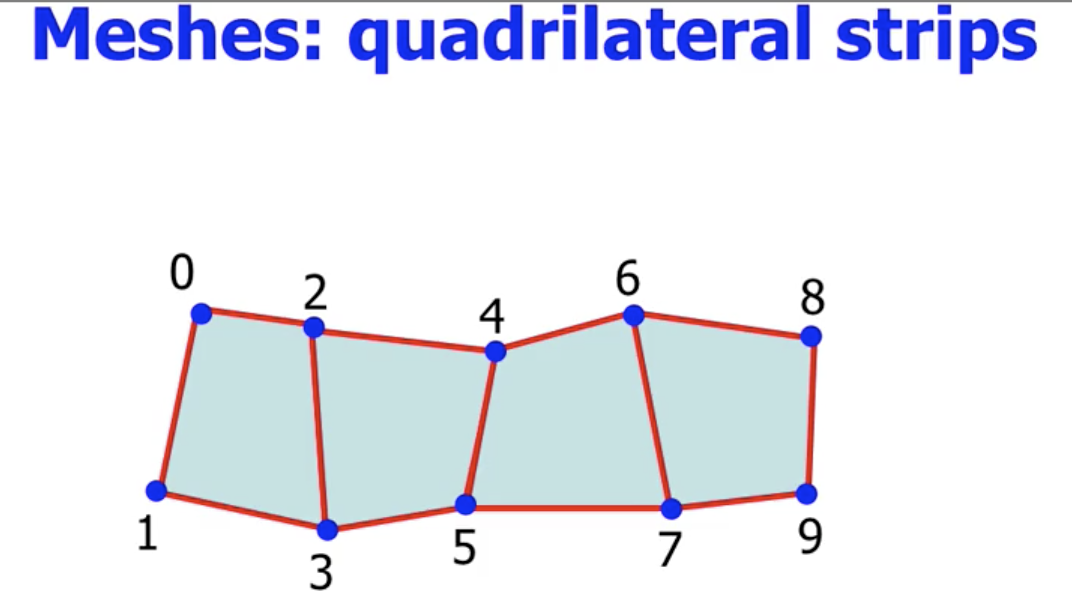
对于 $N$ 个正方形, 这种表示方式只需要存储 $2N+2$ 个顶点.
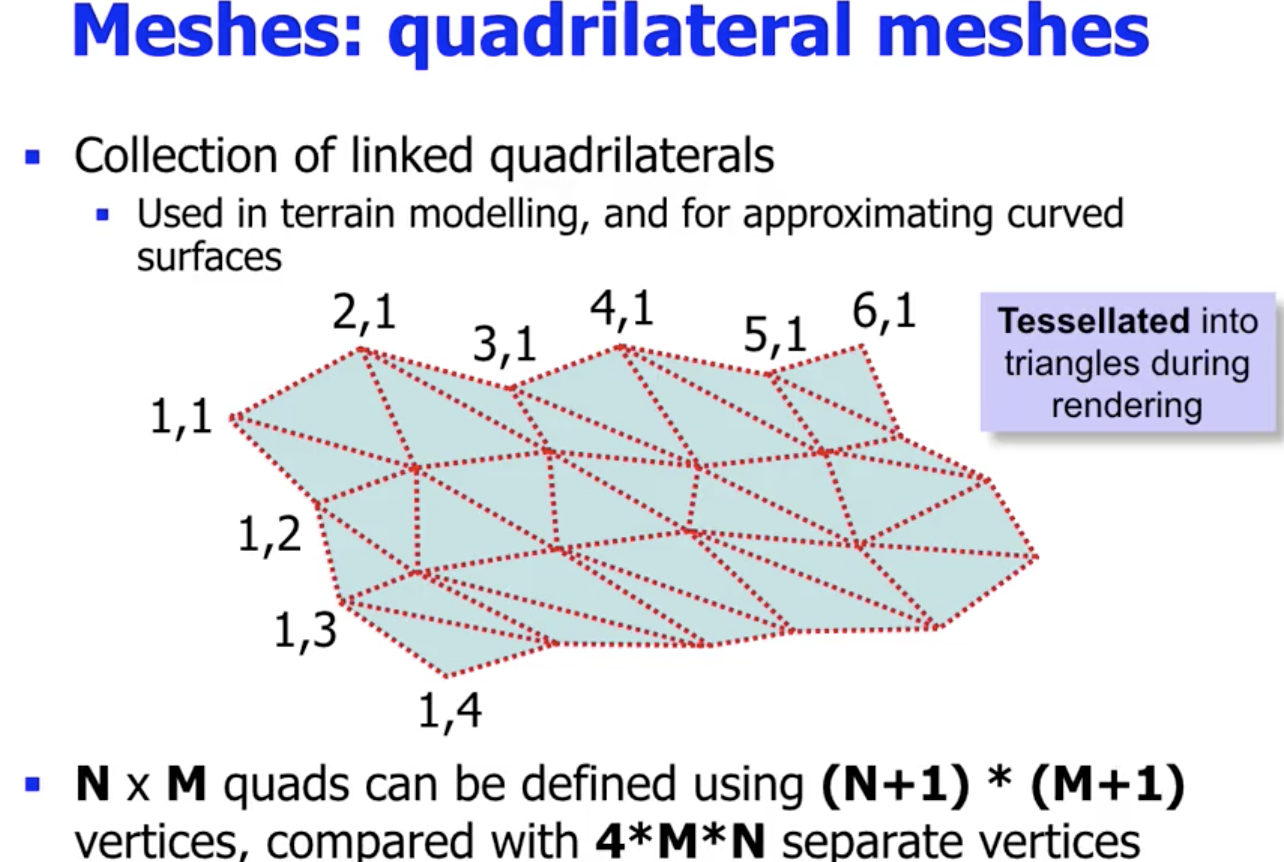
Quadrilateral Meshes
将由正方形组成而且为条状的 Quadrilateral Strips 竖向拼接就得到了 Quadrilateral Meshes. 它可用于 地形建模 和 对曲面近似 (approximating curved surfaces).

对于 $N*M$ 个四边形, 该方法只需存储 $(N+1) \cdot (M+1)$ 个顶点.
而在实际情况中, 当我们需要渲染 Quadrilateral Meshes 时, 由于 三角形更便于渲染, 并且 每个四边形都可沿对角线分割为两个三角形, 因此在这一情形下会首先利用 曲面细分 (Tessellation) 将 Quadrilateral Meshes 切割为多个三角形组成的平面.
扫描转换
在上面一节中, 我们已经讨论了 使用网格高效表示三维模型 的基本思想. 本节讨论如何通过 图形输出流水线 (Viewing Pipeline) 将三维模型输出到二维视场, 也就是屏幕上.
对直线的扫描转换
首先考虑最简单的情况: 将 直线 输出到屏幕上. 由于显示屏使用栅格化的像素阵列显示内容, 因此在显示 非横平竖直 的斜线时, 需要将其 近似. 这一近似过程被称为 扫描转换 (Scan Converting).
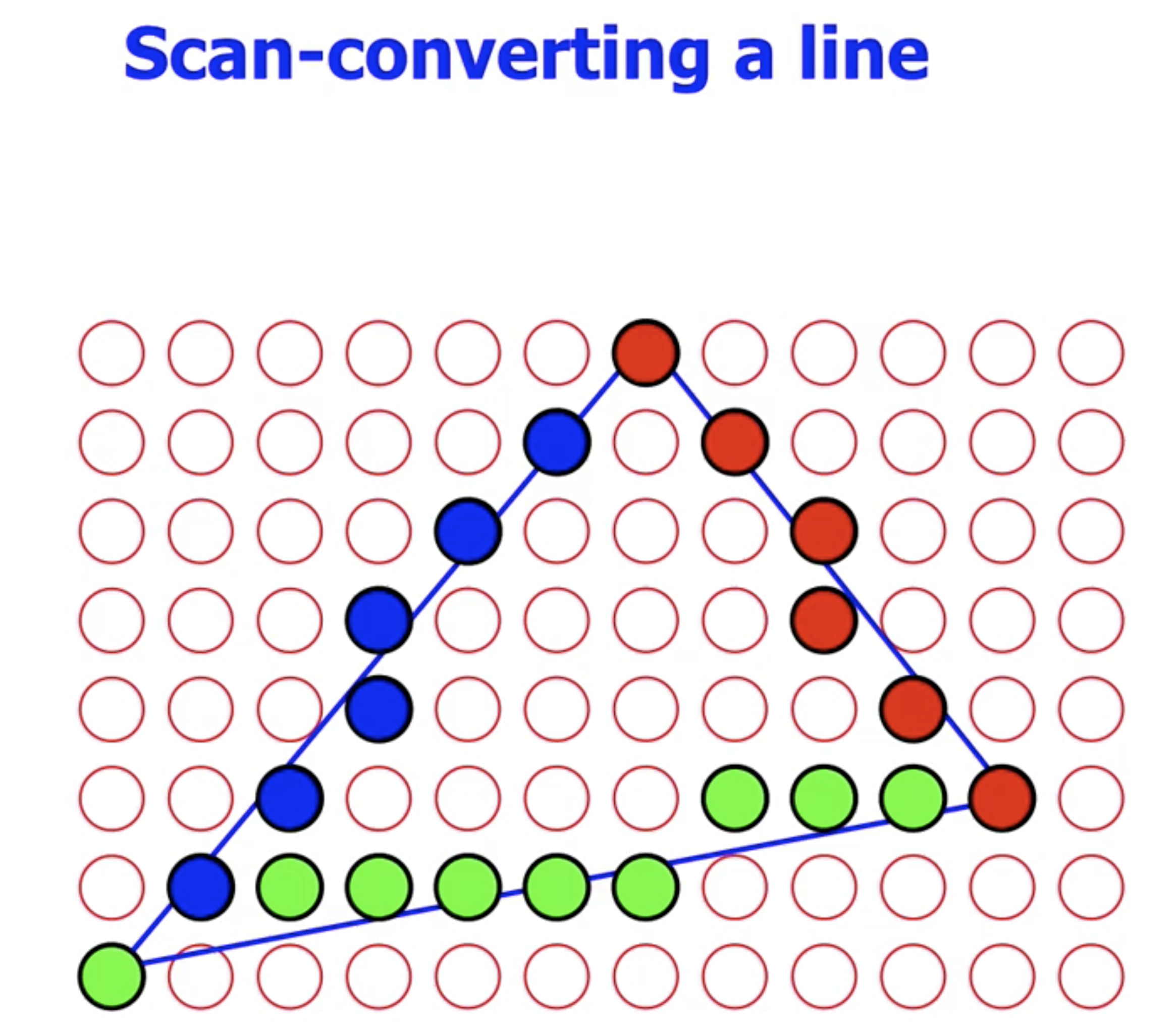
布雷森汉姆直线近似算法
最常用的, 线段扫描转换算法为 布雷森汉姆直线近似算法 (Bresenham's Algorithm):
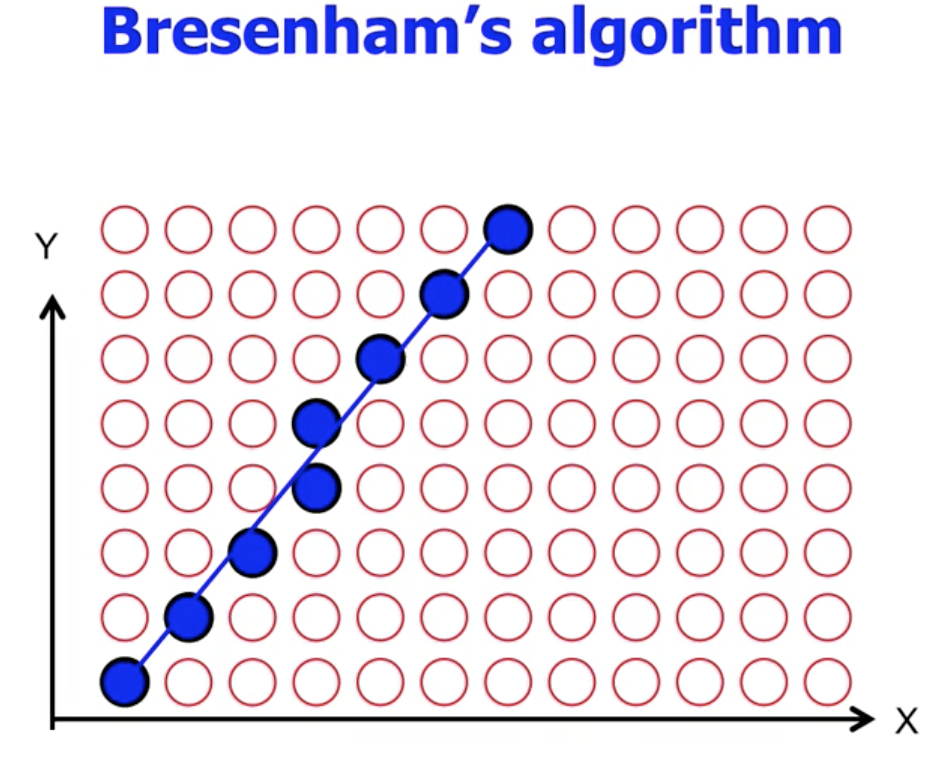
其基本思想如下:
沿着给定直线 $y=mx+c$ 的 水平方向 上 逐像素点地 遍历扫描, 记前一个像素点上对应的 $y$ 轴位置为 $y_n$, 则后一个则为 $y_{n+1} = y_n + m\cdot 1 = y_n+m$.
然后, 考虑向右平移一个像素后对应的 $y$ 轴位置 $y_{n+1}$, 它离哪个像素点最近就选择点亮哪个像素点, 沿 $x$ 轴遍历完之后得到的那些被点亮 (也就是被选择) 的像素点就构成了对这一条直线的近似.
此处注意, 为了确保近似的效果, 我们应当 始终沿着直线相对梯度最小的方式遍历! 比如考虑上面三角形中的绿色边, 我们就应该沿水平轴遍历, 否则沿竖直轴遍历的话就会得到完全不可用的结果.
这也就是所谓的 “Need to swap x and y according to the gradient of the line“.

对多边形的扫描转换
我们随后考虑对多边形的扫描转换问题. 在使用布雷森汉姆算法解决了直线的近似问题后, 我们所需要考虑的主要问题就是 对多边形的上色问题.
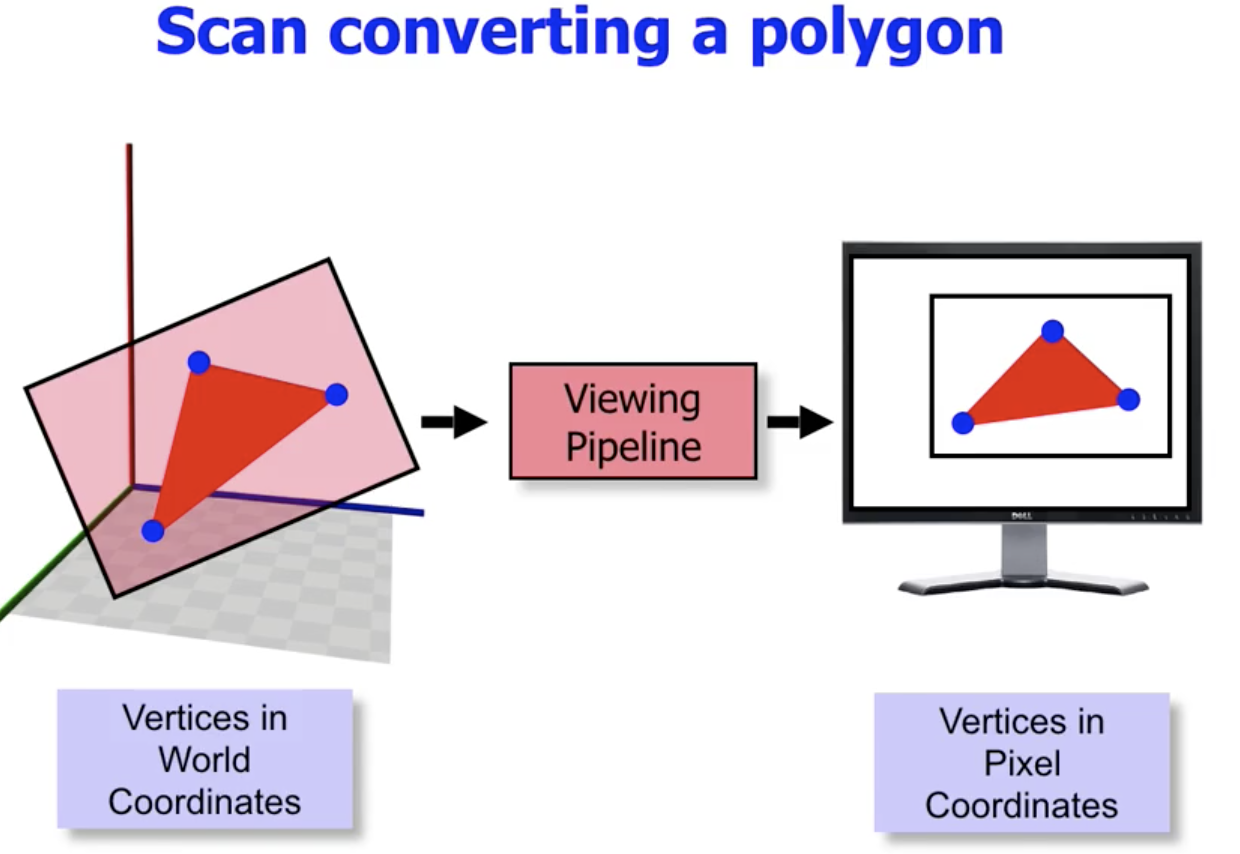
经过图形输出流水线的转换, 我们所得到的参数就是多边形 每个顶点的对应坐标 $(x, y, z)$, 此处我们暂时不使用第三维的信息 (表示这个顶点到 camera 的距离), 只考虑 $(x, y)$, 这个坐标所表示的就是 像素位置.

我们需要解决的问题就是: 如何高效地对多边形顶点围起来的区域上色填充.
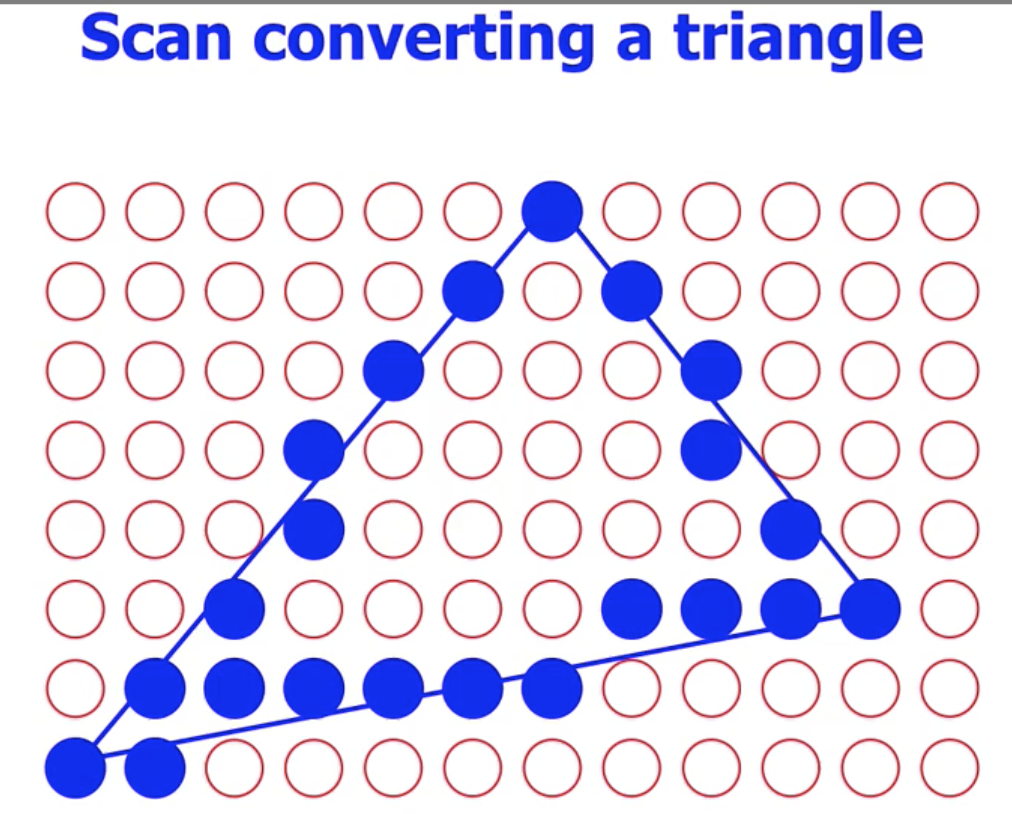
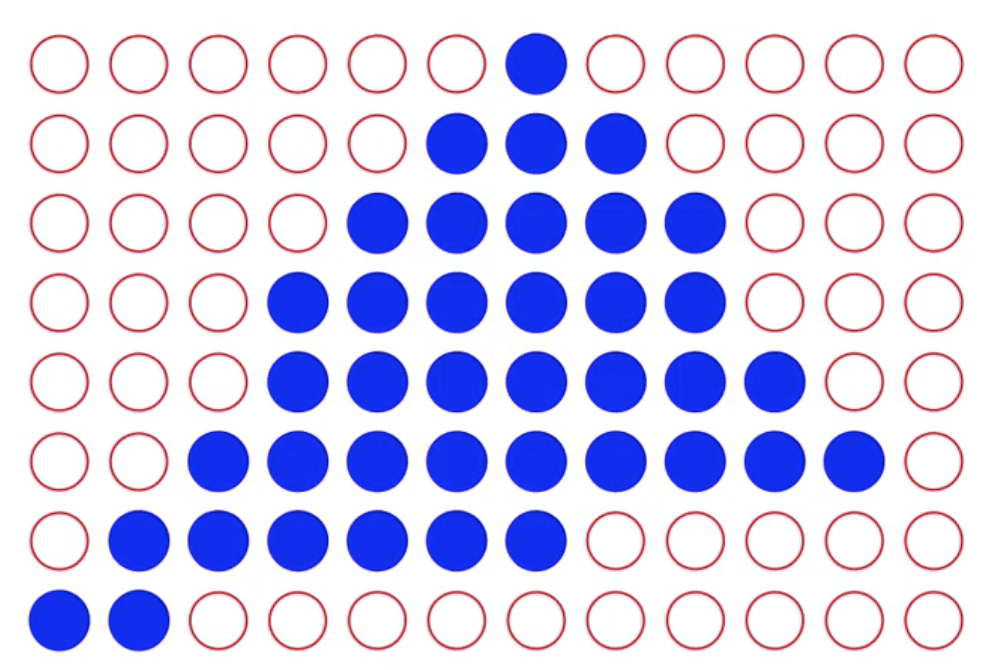
在这里我们讨论扫描线算法. 扫描线算法的基本思路是: 自顶向下 地从顶点开始, 扫描每一行, 然后我们就可以利用多边形边的梯度结合在 $y$ 轴上变化的大小计算 $x$ 轴上相应需要的变化, 从而得到一个在一行内需要填充的像素范围, 如下图所示:
实际上这并不是完整的扫描线算法, 而且扫描线算法其实是相当低效的. 扩展阅读: 这里
移除被隐藏面 (Hidden Surface Removal)
至此, 我们已经将用来表示曲面的多边形扫描转换到了屏幕上. 我们进一步需要考虑的问题是: 由于透视角度的关系我们观察三维物体时总会出现 “一些面被其他一些面所遮挡” 的问题. 因此我们需要考虑, 如何检测并避免渲染这些 “在 camera 的当前角度看不见的线”, 这也就是 Hidden Surface Removal.

在本课程中我们讨论第二种标准化的技术路径: 通过存储和对比 ”深度信息“ 避免渲染本不该被看到的面.
Z-buffer
Z-buffer (depth-buffer) 是用来 存储每个像素深度信息 的数据结构. 注意, 此处的 “像素” 不是指屏幕上的对应像素, 而是 所有被扫描转换的多边形上的每一个像素.
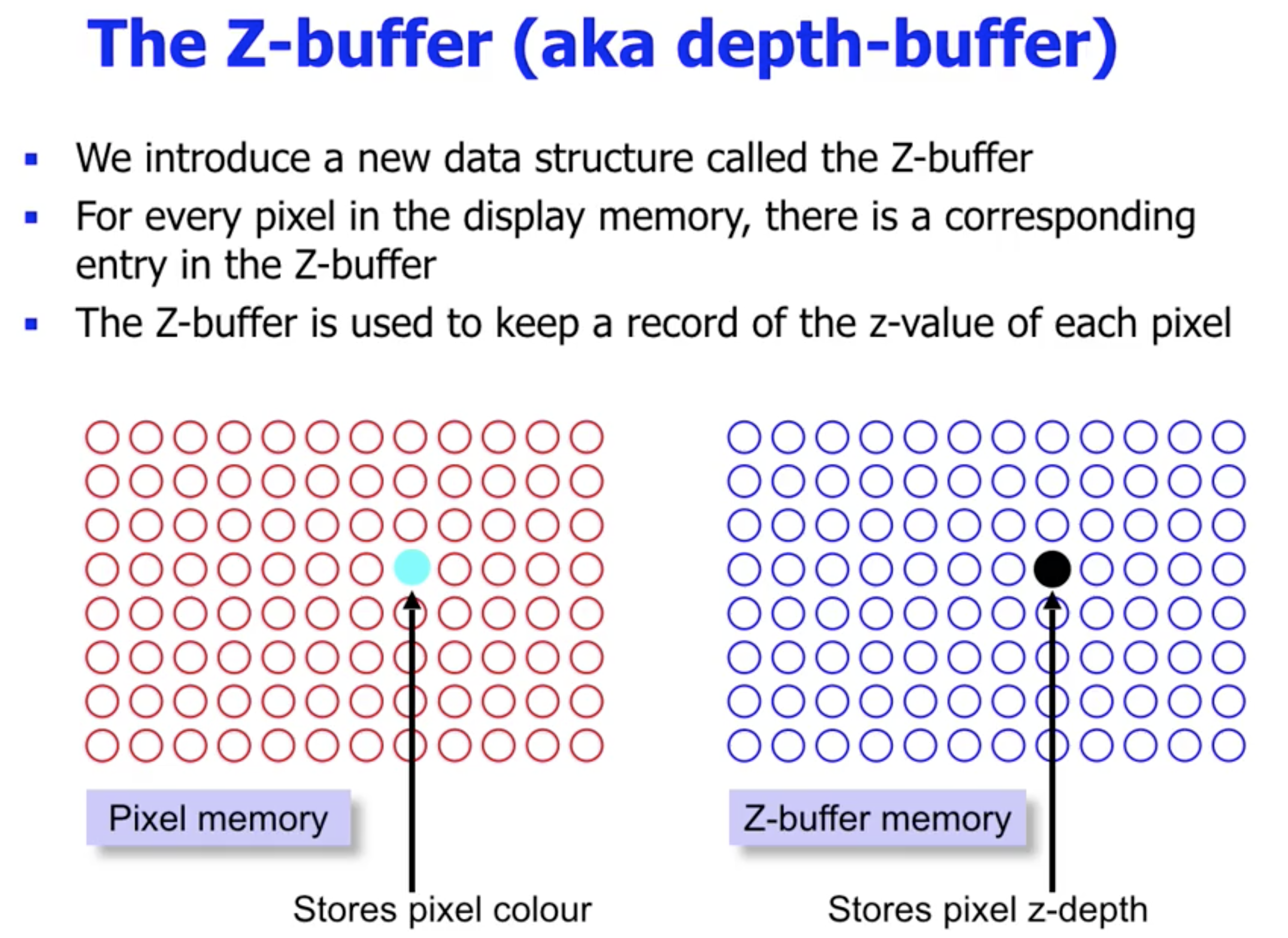
Z-buffer 算法
Z-buffer 的基本思想是: 将屏幕像素深度初始化为最深, 然后遍历所有多边形上的所有像素.
对于每个像素, 将它的深度信息和屏幕对应像素点的深度信息对比, 如果多边形上的像素深度信息更低, 说明它在视觉角度上更靠近 camera, 会遮挡它后面的内容, 所以此时屏幕对应像素点的颜色和深度信息都要被更新为多边形上的这个对应像素点, 也就是执行了渲染;
而如果多边形上的某个像素点的深度大于屏幕上的对应像素点, 说明它被遮挡了, 所以此时无需渲染.

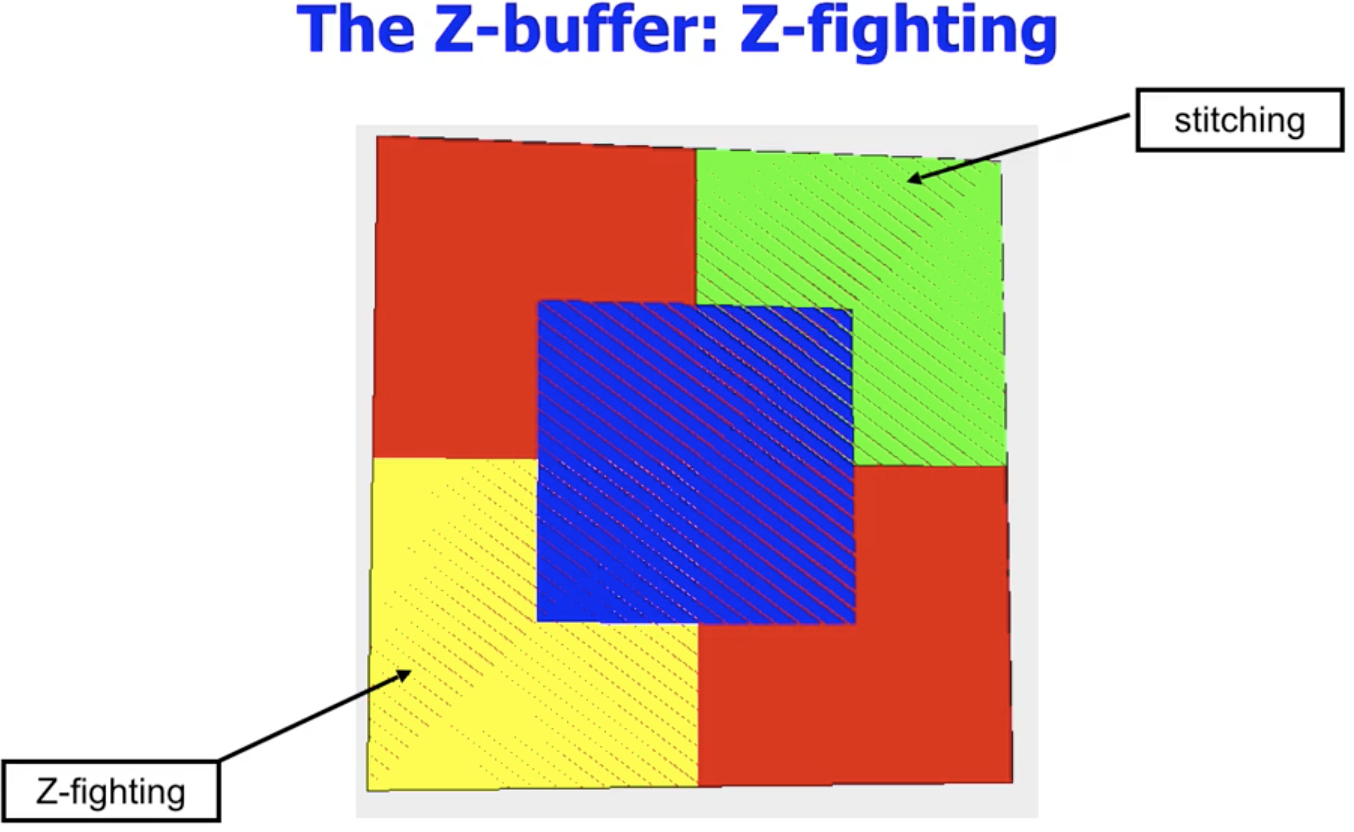
需要注意: 当 两个不同多边形上像素点的深度信息非常接近 时, 就可能出现渲染错误的现象, 图形管线无法确定两个面中谁该覆盖谁, 因此有时渲染第一个, 有时渲染第二个, 导致图像交替闪烁, 称这种情况为 Z-fighting.
对复杂场景的建模
之前我们提到, 多边形浓汤表示法的一个明显缺陷是不包含模型/场景的语义信息. 在对复杂场景进行建模时, 由于它涉及多个模型 (对象), 因此使用 基于逻辑划分的层级结构 就可以保存语义信息, 同时实现建模的模块化.
考虑下面的例子: 对分子的建模可以被划分为对原子和化学键的建模.
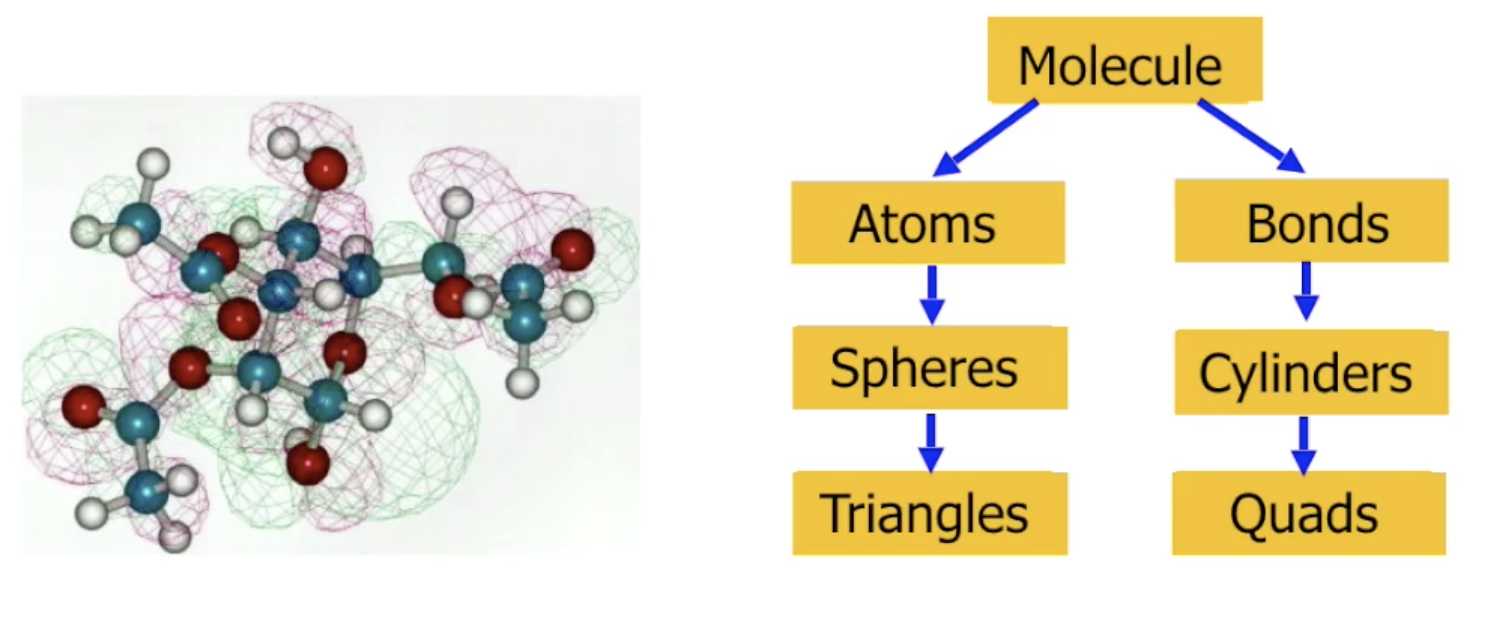
更进一步地, 我们可以对单个物体进行层级上的拆解. 如下图所示:
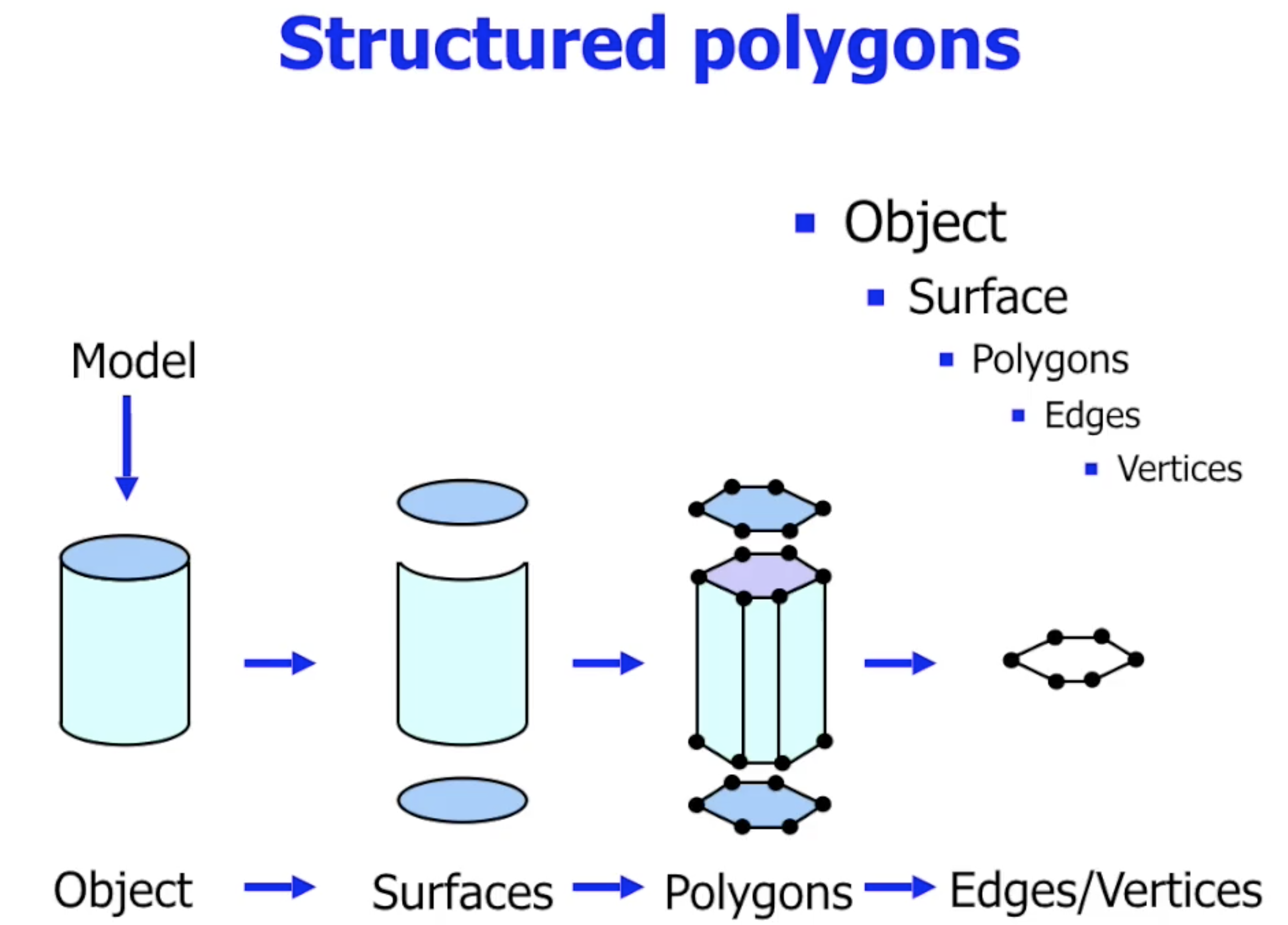
考虑下面的例子. 假设我们需要表示某个由多边形组成的网格结构:
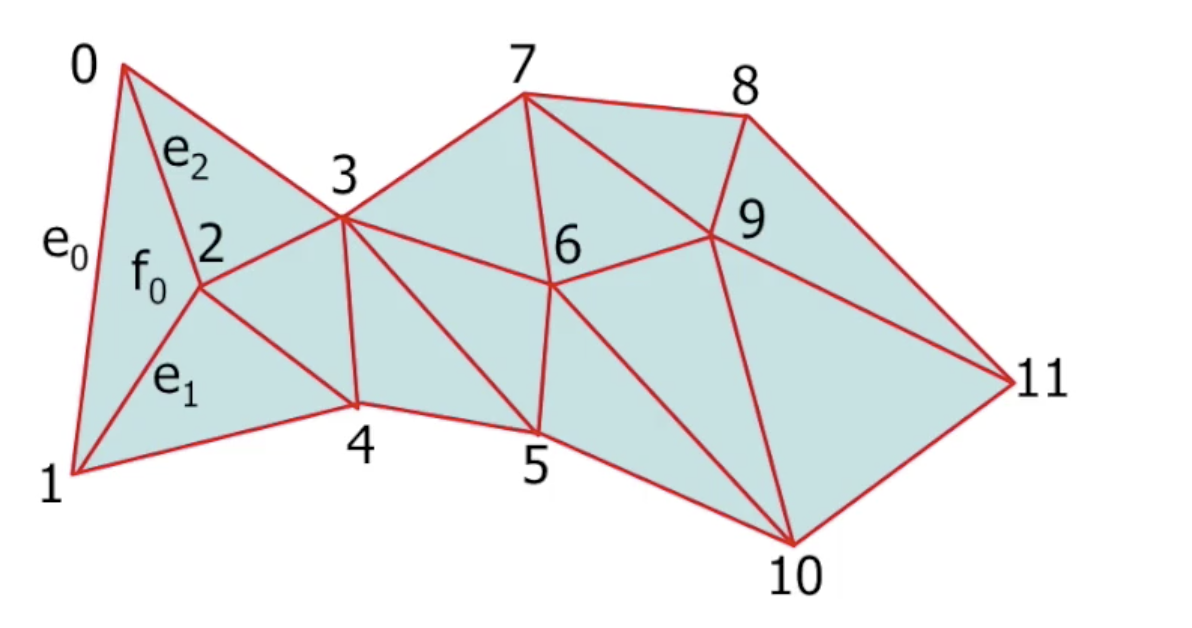
它首先可以被拆分为多个部分. 考虑 $0-1-3-4$ 这个部分:
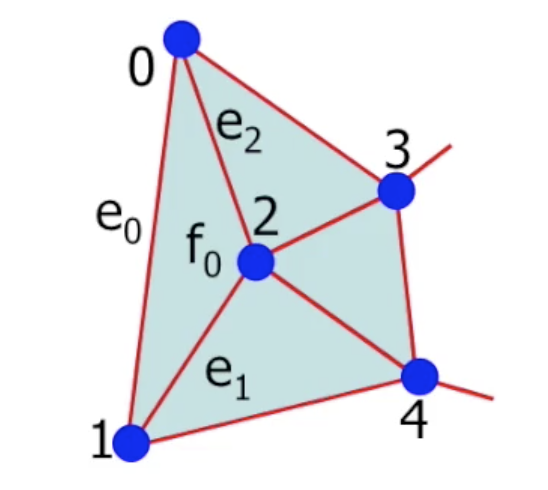
再进一步考虑这个子网格中的一个面 $f_0$:
它由一个多边形 (三角形) $0-1-2$ 组成, 有三个顶点和三条边. 因此我们可以得到下列的关系:
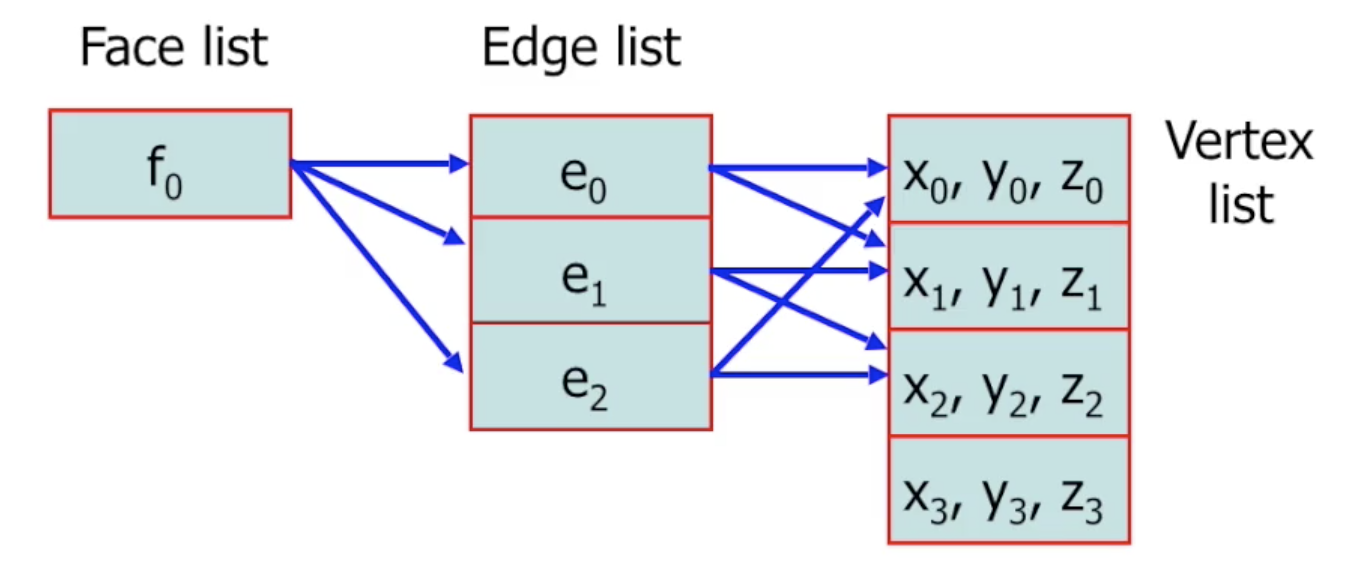
其中第三列所表示的是 (整个网格的) 顶点列表, 每个顶点都用一个三维坐标表示.
