一阶逻辑推理

1. 一阶逻辑推理的一般框架: 饱和 (Saturation) 与 子句化 (Clausification)

在本节中, 我们将把前四周内所介绍的, 关于一阶逻辑和前向/反向链式推理的思想综合为 用于一阶逻辑推理的一般框架: 它将包括一个通过驳斥 (refutation) 建立蕴含关系的, 应用在子句上的 饱和算法, 以及一个用于将一般地一阶公式转换为子句的 子句化方法.

需要注意, 在此我们讨论的 子句 定义不受前一章中的限制, 不仅局限于 Horn 子句 (Horn Clause) 或明确子句 (Definite Clause). 我们将在子句化过程中说明: 任何形式的一阶公式都可被表示为一系列子句组成的集合.

下面我们首先引入 基于反驳的推理 和 饱和 的概念.

1.1 基于反驳的推理

首先回顾一些基本定义和记号:

1. 文字 指原子或原子的取反 (Negation).
2. 子句 指一系列文字的析取, 隐式地被全称量词量化.
3. 称两个原子 $l_1$, $l_2$ 联合, 若存在替换 $\theta$ 使 $l_1 \theta, l_2 \theta$ 在语法上相同.
4. 若某两个原子 $l_1, l_2$ 能够联合, 则必存在一个 最一般的联合子 $mgu(l_1, l_2)$.

5. 归结原则 (Resolution) 可用于具备下列形式的子句上:

   $$\frac{\neg I_1 \vee C ~~~ I_2 \vee D}{(C \vee D)\theta}, ~~ \theta = \text{mgu}(I_1, I_2).$$

   且可以证明归结原则是 正确的 (sound), 因为结论对任何前件条件 (Premises) 的模型都成立.

6. 一般地, 为了避免命名冲突, 我们需要在对前件条件应用归结原则前将它们重命名以确保不存在名称相同的变量.

下面我们考虑通过 反驳 (Refutation) 实现推理的推理方法. 其实质是: 通过否定我们希望证明为真地陈述的反面, 来隐式地达成对 “陈述为真” 的证明.

如: 我们在证明陈述

时, 如果通过 证明 $\Gamma \cup {\neg \phi}$ 是不一致的 来说明原陈述成立, 就是在使用 基于反驳的推理方法.

而证明 $\Gamma \cup {\neg \phi}$ 不一致的方法是: 将其作为知识库, 不断地从中试图推导出所蕴含的新事实 , 如果直到 无法从中再推导出任何它所蕴含的新结论 为止, 我们都 没有 推出矛盾 False, 则说明式子 $\Gamma \cup {\neg \phi}$ 是可满足的, 即

反之, 只要推导出 False, 就可以说明它是不一致的, 也就证明

这种类似于前向链式推理的检测方法通过 不断地 从给定公式形成的知识库中推导出新的蕴含关系, 除非中途推导出 False 否则会 一直穷尽 到没有新的蕴含关系可推为止, 因此得名 “饱和推理” (Saturation).

考虑下面的例子:

直到目前为止, 我们介绍的任何一种推理方法都要求查询语句 中每个变量都被全称量词修饰 (Universal unit) 或 为合取范式 (Conjunctive Queries). 下面考虑如何对更一般的查询语句执行推理, 这也是 定理证明 (Theorem Proving) 的需求.

我们认为 定理证明 就是 自动推理 (Automated Reasoning) 中的一个分支, 其关注点是寻找 (知识库, 或称理论) 所蕴含的 陈述 (Statement) 的证明 (Proofs).

需要注意, 定理证明 由于起源于数理逻辑, 因此在部分概念的术语上和 自动推理 有所不同: 自动推理领域中的 知识库 在定理证明领域中被称为 理论 (Theory), 而任何蕴含于 理论 中的 陈述 (Statement) 都被称为一个 定理 (Theorem), 因此自动推理过程就被视为 “基于理论寻找定理的证明”.

下面简介一个简单的, 基于饱和推理的定理证明算法的流程:

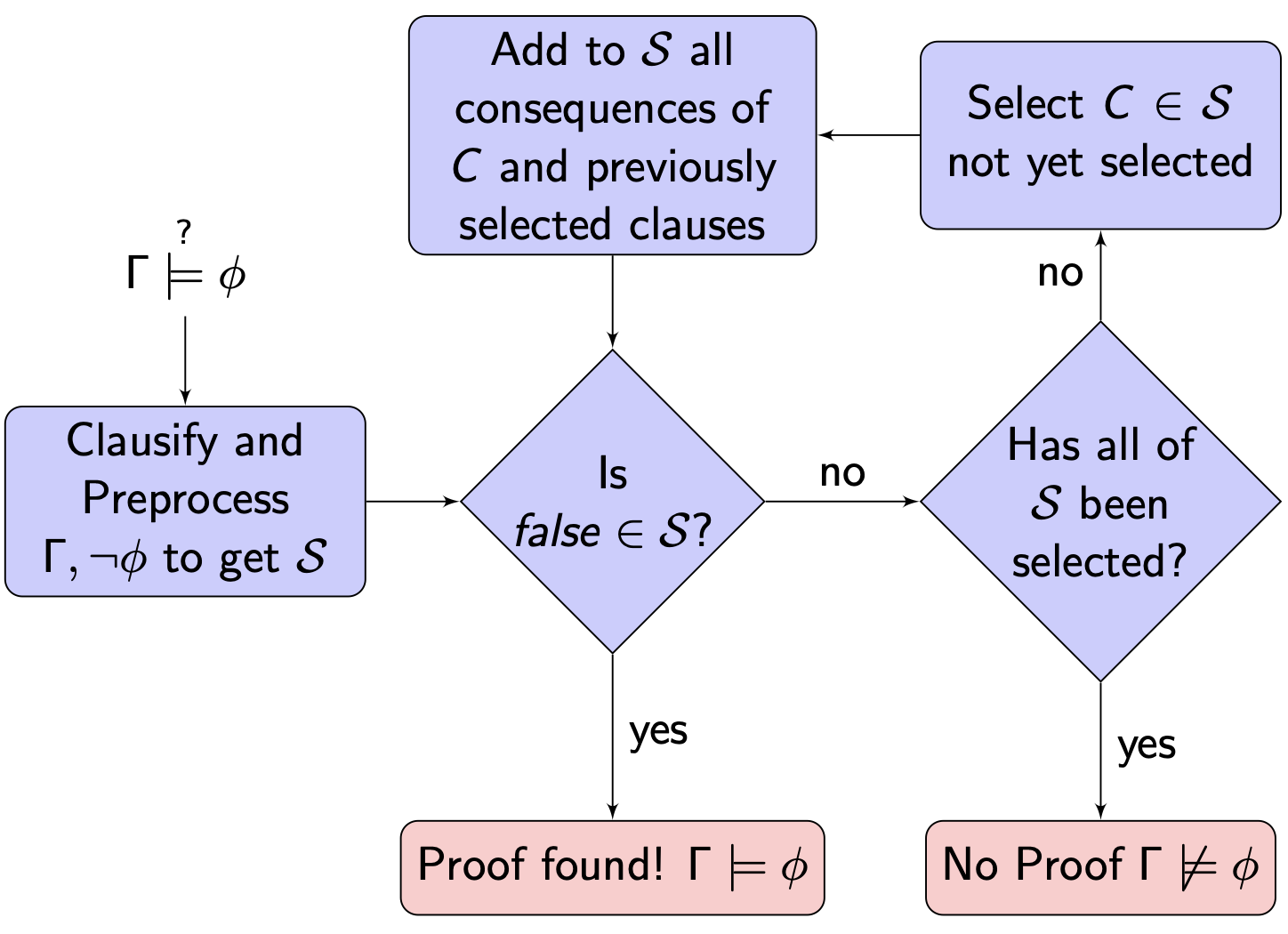
1.2 饱和

假设待判断可满足性的陈述为

执行饱和推理的目的是, 确认 理论以及所有从理论中蕴含出的陈述组成的集合 $S$ 中是否有 False.

下面简述饱和推理的基本流程:

1. 将 $S$ 拆分为待蕴含的 NotDone 和已经过蕴含处理, 不会再得出新结论的陈述组成的集合 Done 两个部分.

   在初始化时, 自然地将 NotDone 初始化为

   $$\Gamma \cup \{\neg \phi\}$$

   并将 Done 初始化为 $\emptyset$.

2. 将 NotDone 经过转化和预处理 变为一系列子句组成的集合.
3. 检查经过转换后的集合, 若已经发现 False 则直接返回 valid.
4. 若不能直接从第三步中得出结论, 则从 NotDone 中 基于某些规则 选取一个子句 $C$, 将其移入 Done.
5. 执行 $C$ 与 Done 中任何其他子句之间所能执行的所有的推导规则 (Inference), 如归结原则, 并将生成的所有有意义的新结论放到 NotDone 中以备后续检查.
6. 检查 NotDone 集合是否为空. 若不为空的话, 返回到第三步.
7. 最后, 如果直到所有的定理及其归纳出的衍生结论均被检查后仍未归纳出 False, 则返回 not valid.

我们将在下一节中详细解释如何实现第二步中的 转化和预处理 和第四步中 选取新子句的规则, 在后面的章节中进一步地解释和介绍第五步中 对子句的推导原则.

下面给出一个更具体的饱和推理算法的伪代码:

饱和推理与前向链式推理和反向链式推理之间的两个关键不同点是:

1. 饱和推理是 有目标的 (Goal-Directed): 和前向链式推理 盲目地 尽可能地推导知识库所蕴含的新结论不同, 从一开始饱和推理的目标就是 $\text{goal}(\neg \phi)$.

   因此, 饱和推理在达成目标之后就会立即终止并返回结果, 并且还可以反向推理.

2. 饱和推理对搜索路径中的新节点的选择是 基于最优标准 (Best-First) 的.

2.

REFERENCES:

Forward Logic Programming

• Previous
  基于知识组织的人工智能：Prolog 速成
• Next
  计算机图形学导论：渲染多边形