几何变换与着色器
向量, 坐标系和坐标表示
笛卡尔坐标系系统
首先考虑 三维笛卡尔坐标系:
在本课程中, 我们使用的笛卡尔坐标系遵循 右手定则: 手心正对自己, 则 食指对应 $Y$ 轴, 拇指对应 $X$ 轴, 中指对应 $Z$ 轴, 如下图所示:
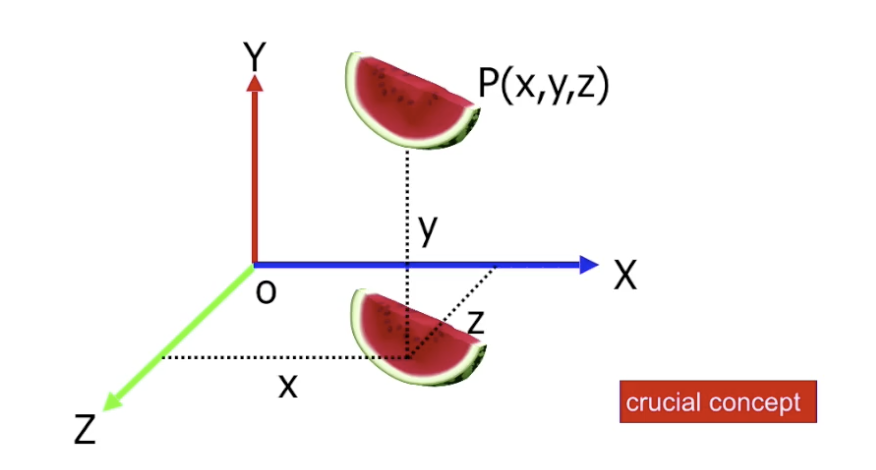
而在上述的坐标系中, 我们可以使用 以三轴坐标组成的元组 表示 空间中的 向量或点:
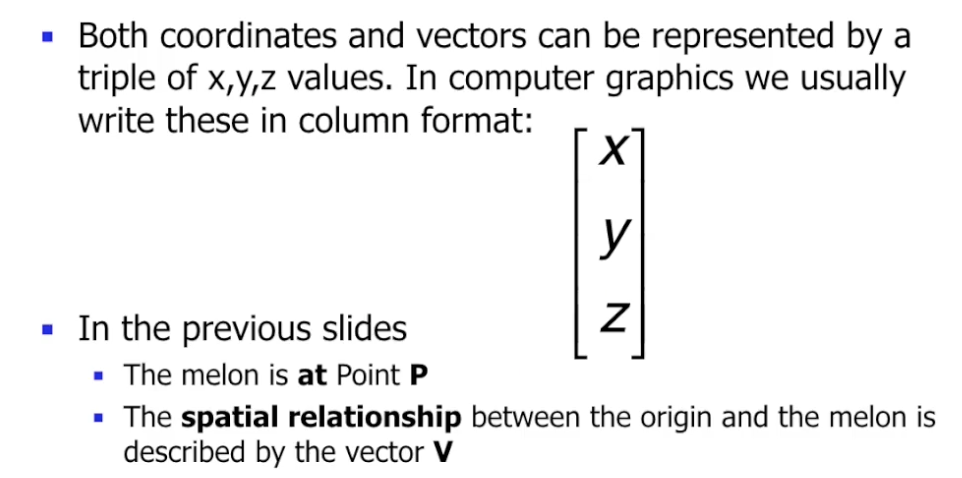
而需要注意的是, 向量或点的表示有两种可能形式. 选择不同的表示形式会相应影响后续表示为矩阵运算的几何变换的实现.

平移变换 Translation
空间中的 平移变换 是通过对 相应坐标轴的对应坐标值加上 offset 实现的:
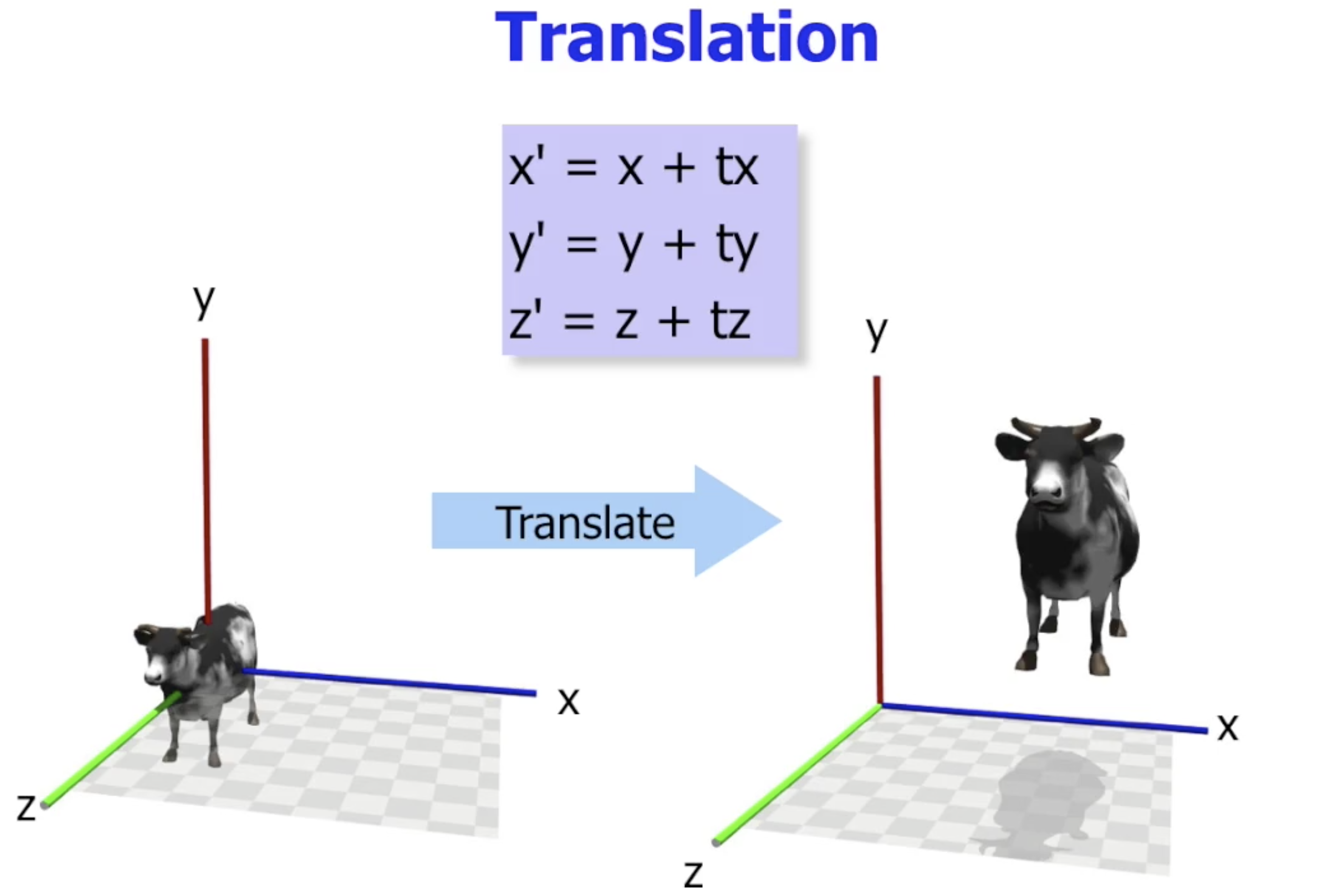
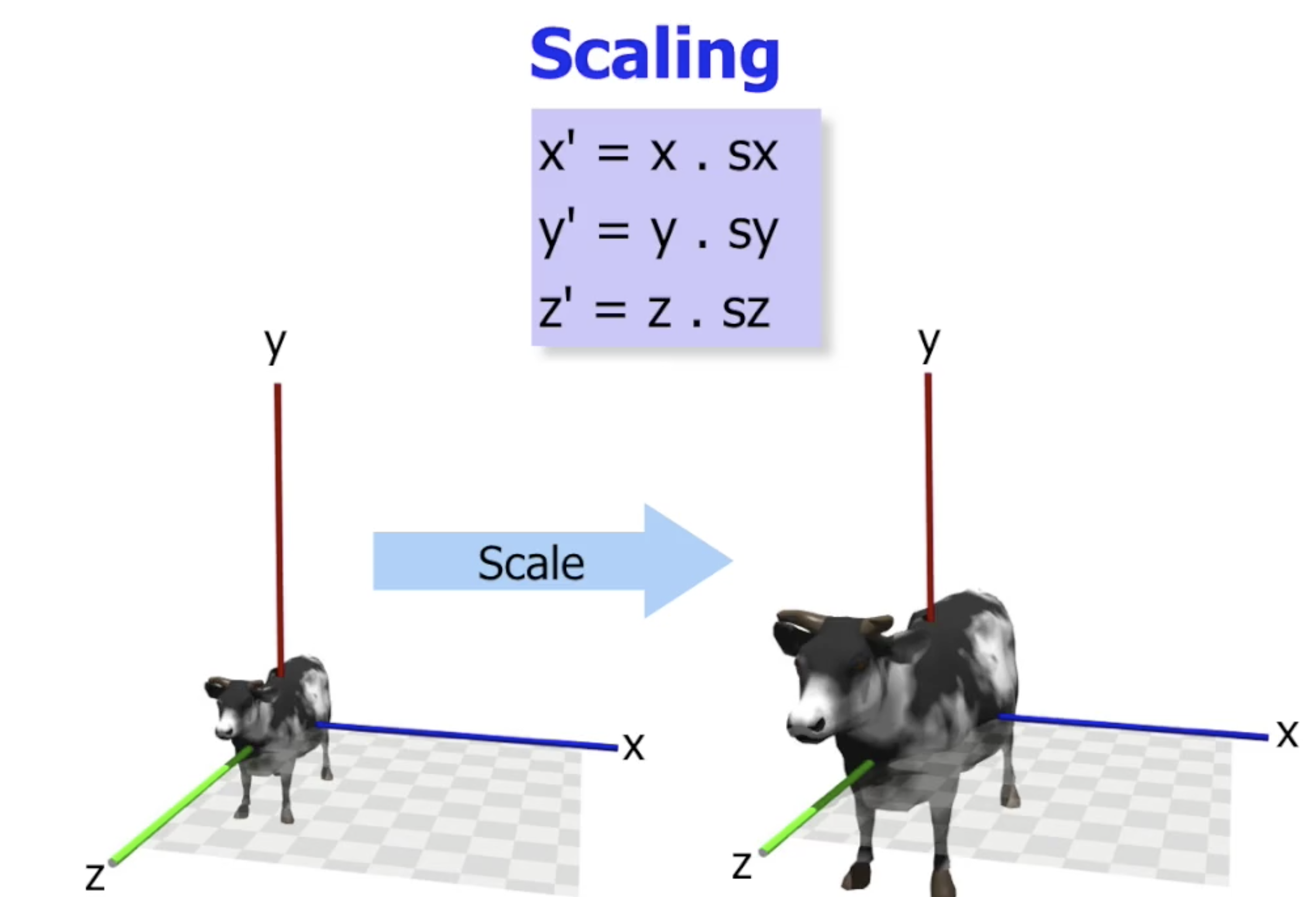
缩放变换 Scaling
而分别对相应坐标值乘上系数, 就可以实现 $x, y, z$ 轴的 拉伸, 当三轴系数相同时, 拉伸的效果就是缩放:
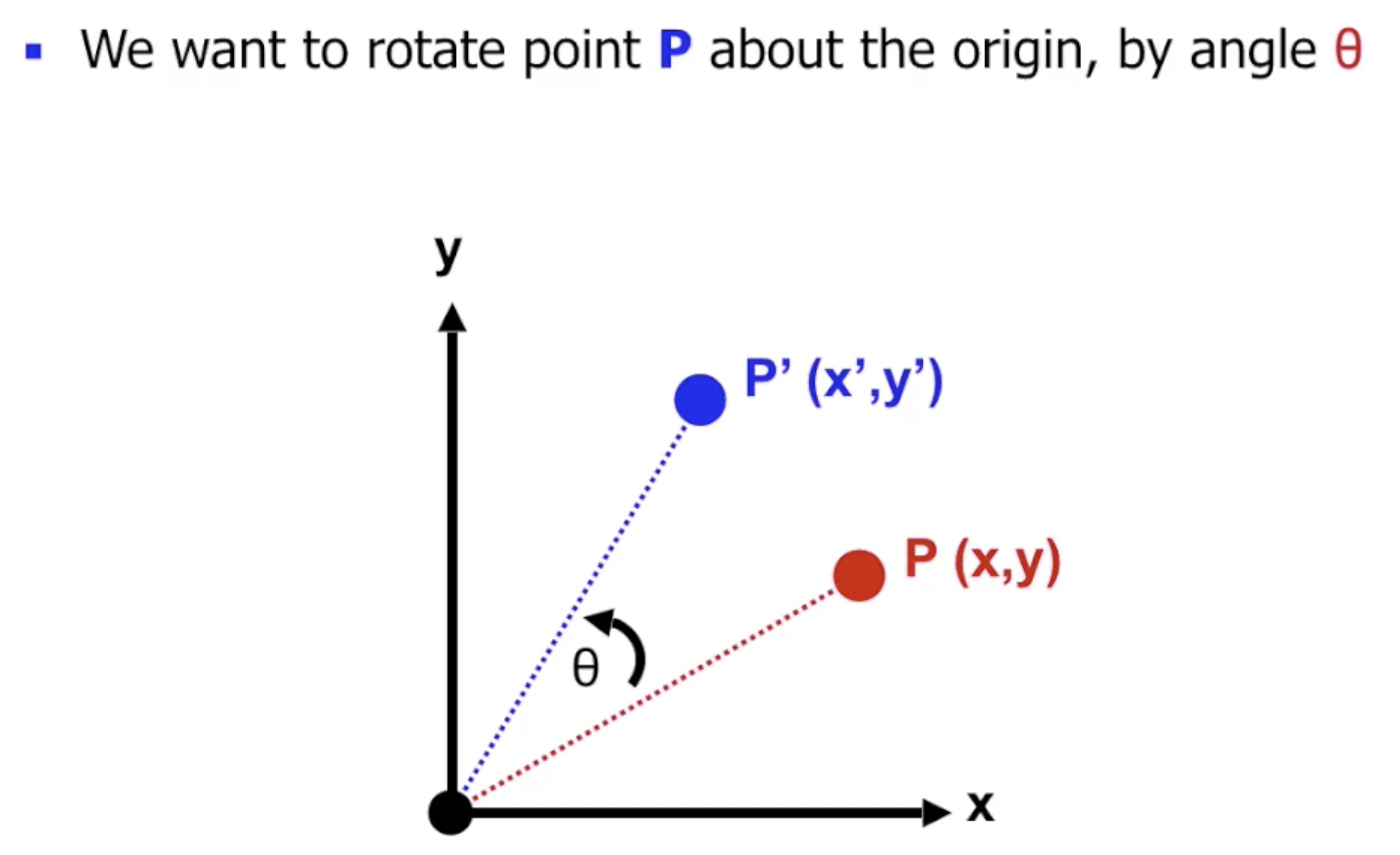
旋转变换 Rotation
旋转变换分为 二维/三维 空间中的 直角坐标/极坐标 变换.
二维旋转变换
首先考虑 二维平面中的极坐标系下 的旋转变换.
由于在极坐标中任何点由 极角 $\theta$ 和 极轴 唯一表示, 因此对该点执行旋转变换 只需改变其对应极角的值.
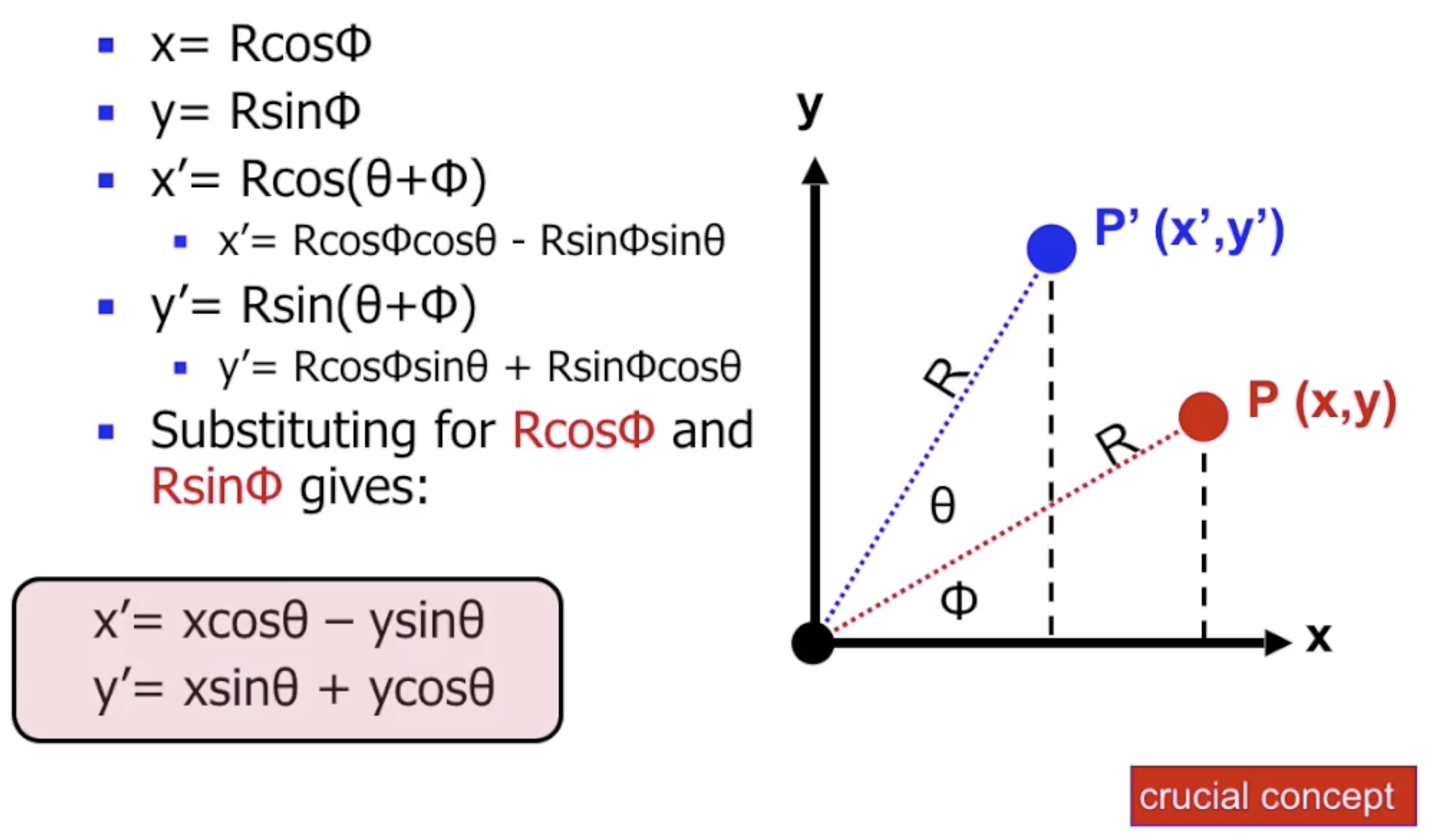
而在直角坐标系中的情况就会更加复杂. 由于在直角坐标中我们对任何点坐标的表示 实际上都是从原点到该点的线段在 $x$ 和 $y$ 轴上的投影, 因此在进行旋转时需要执行一些比较复杂的三角函数运算;
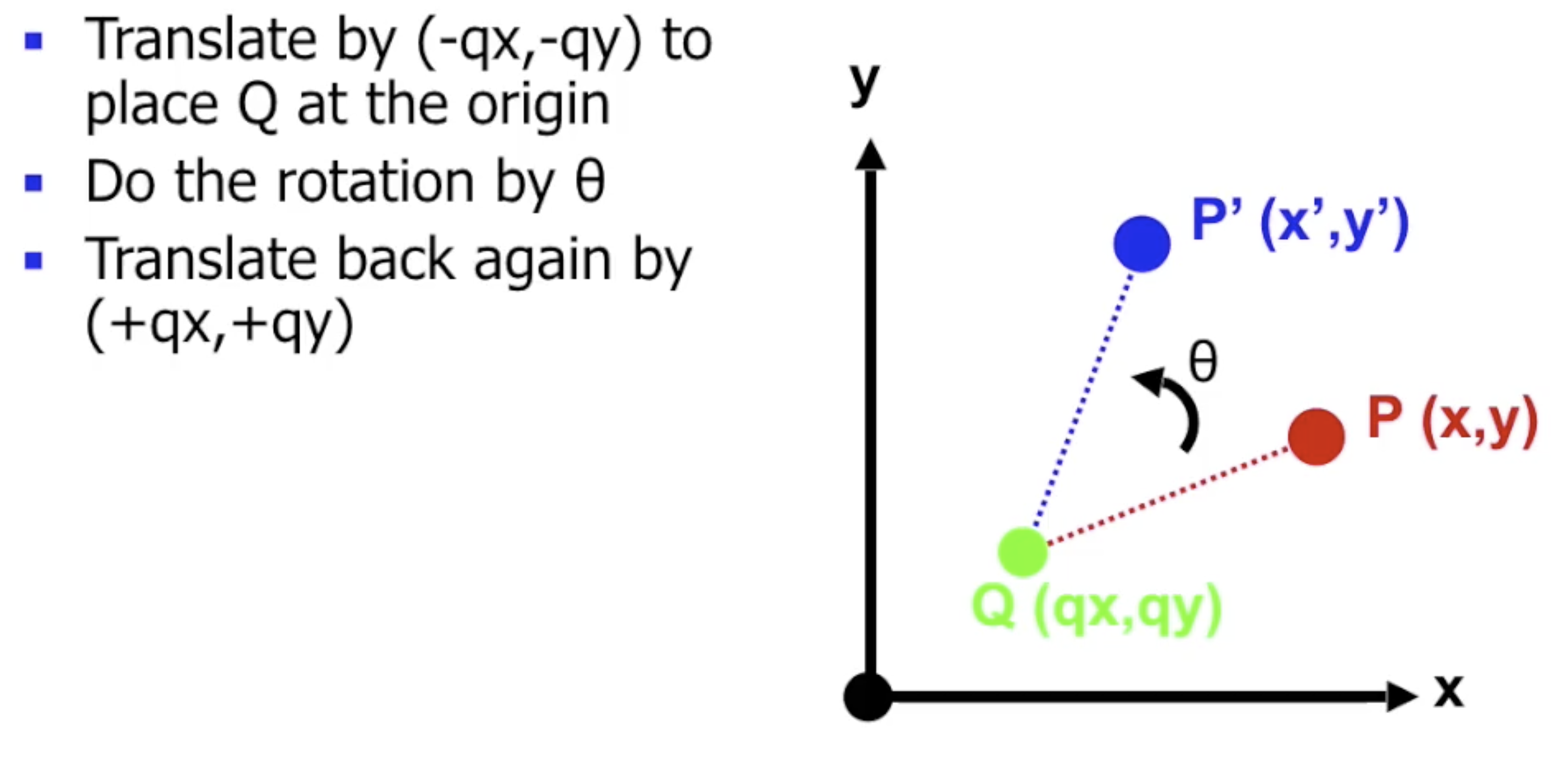
最后考虑 以二维平面中任意点为中心 的旋转变换.
处理这种旋转变换时, 需要 先将这个系统 “平移”回原点, 执行变换后再平移回去.
三维旋转变换
而在 三维空间中的, 基于直角坐标系的 二维旋转变换和二维空间中的差别不大:
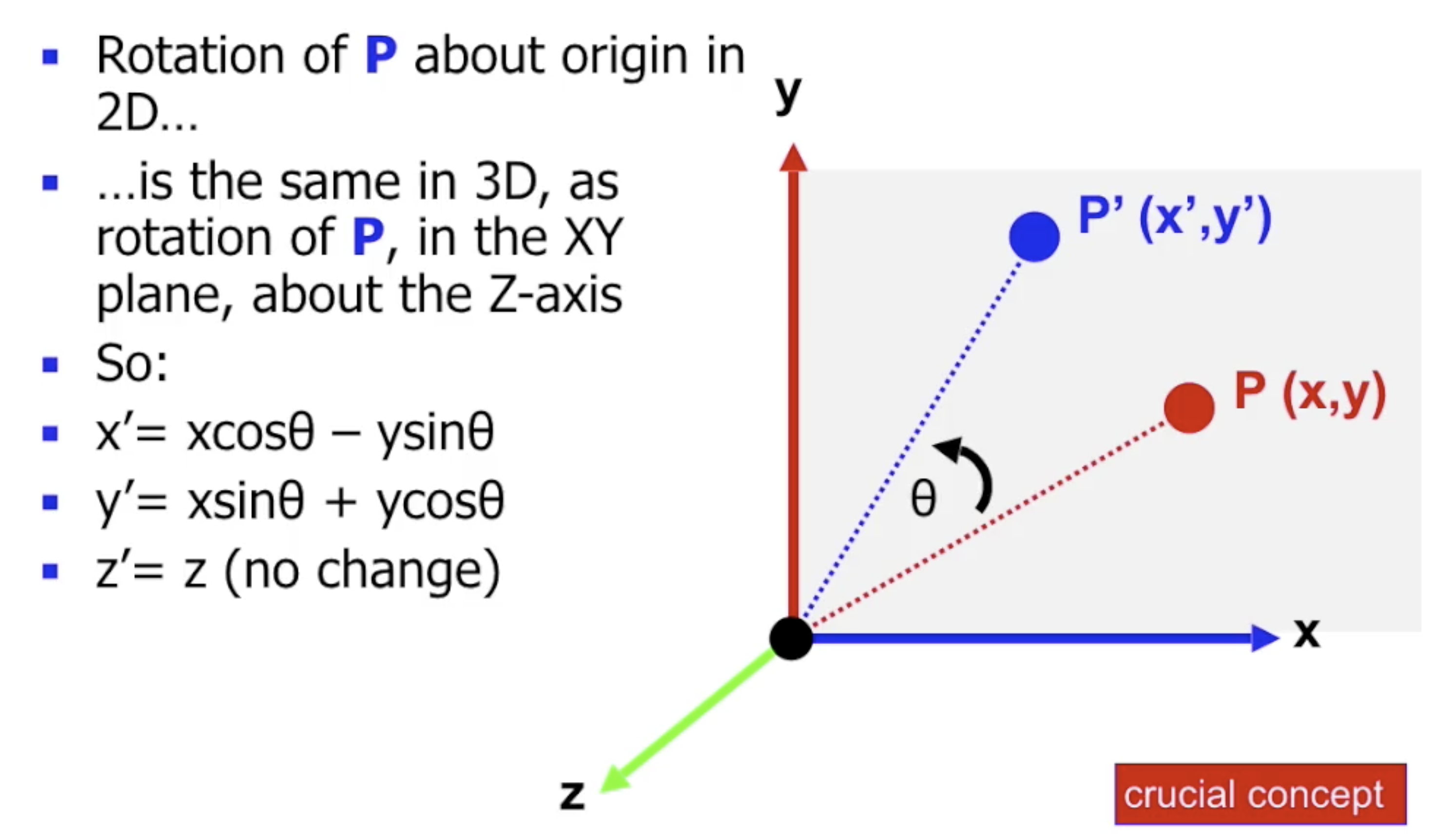
需要注意, 在三维空间中执行的任何旋转变换实际上都可视为 多个沿着某个固定轴执行的二维旋转变换的合成.
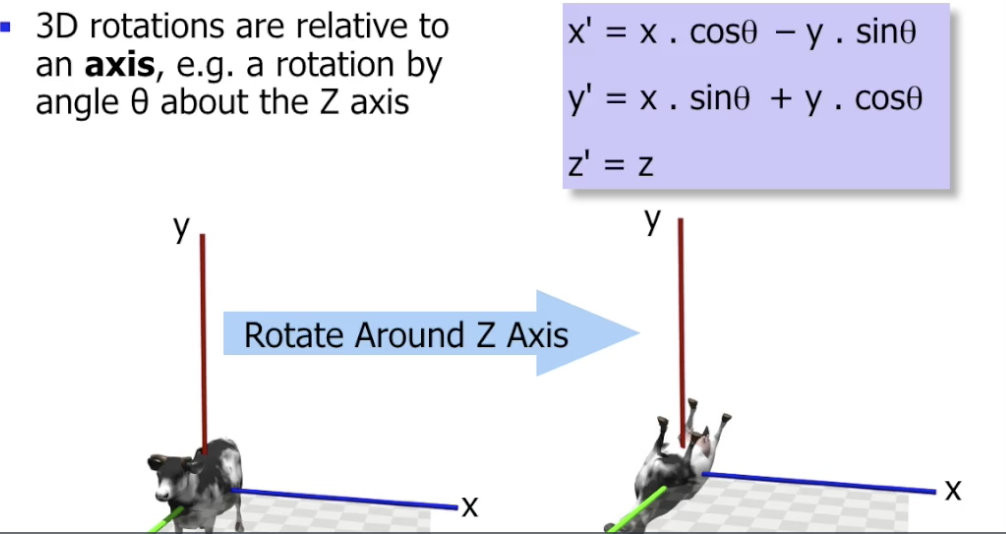
基于标准坐标下几何变换的矩阵表示
下面考虑基于标准坐标下不同几何变换的矩阵表示.
回顾上述内容, 可知:
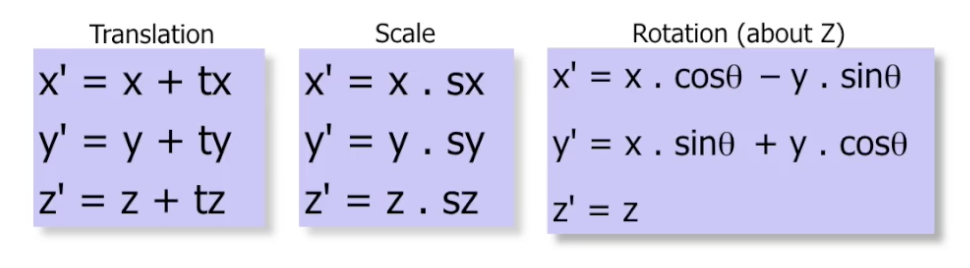
进一步地就可将对不同坐标值的运算 封装为矩阵运算:
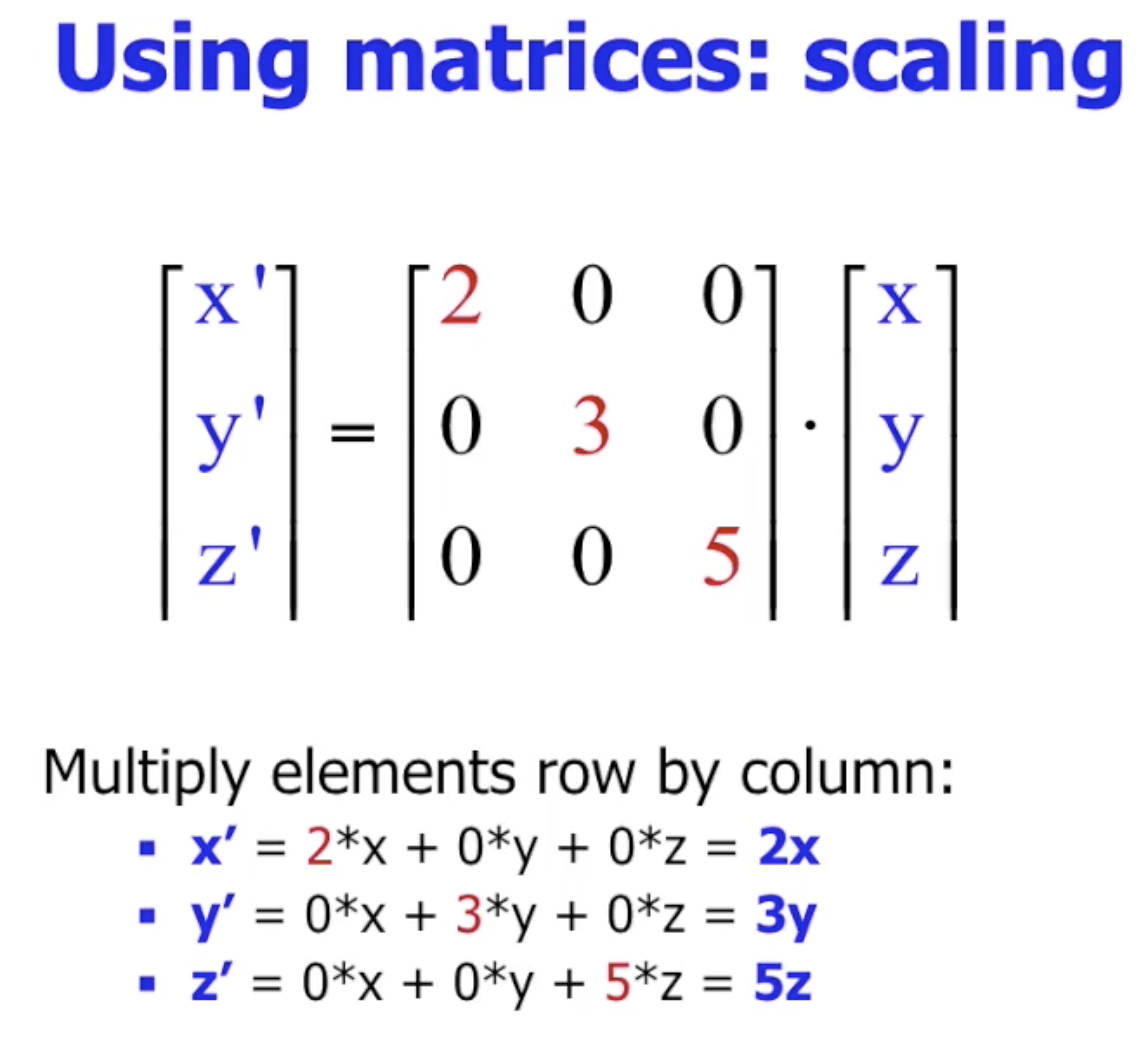

而我们可以注意到, 我们无法使用标准坐标, 实现 平移变换的矩阵表示.
为了解决这一问题, 我们引入 齐次坐标:

基于齐次坐标下几何变换的矩阵表示
引入齐次坐标的根本目的是 确保常用的几何变换的矩阵表示具有一致性.
齐次坐标和标准坐标的差别在于, 它 多出了一个维度, 用以提供平移变换的 offset.
但是, 一般这个多出的维度值 都会被固定为 $1$, 而当在一些特殊情况下它不为 $1$ 时, 就需要 将其正则化为 $1$:

因此基于齐次坐标下不同几何变换的矩阵表示分别如下:
-
缩放矩阵
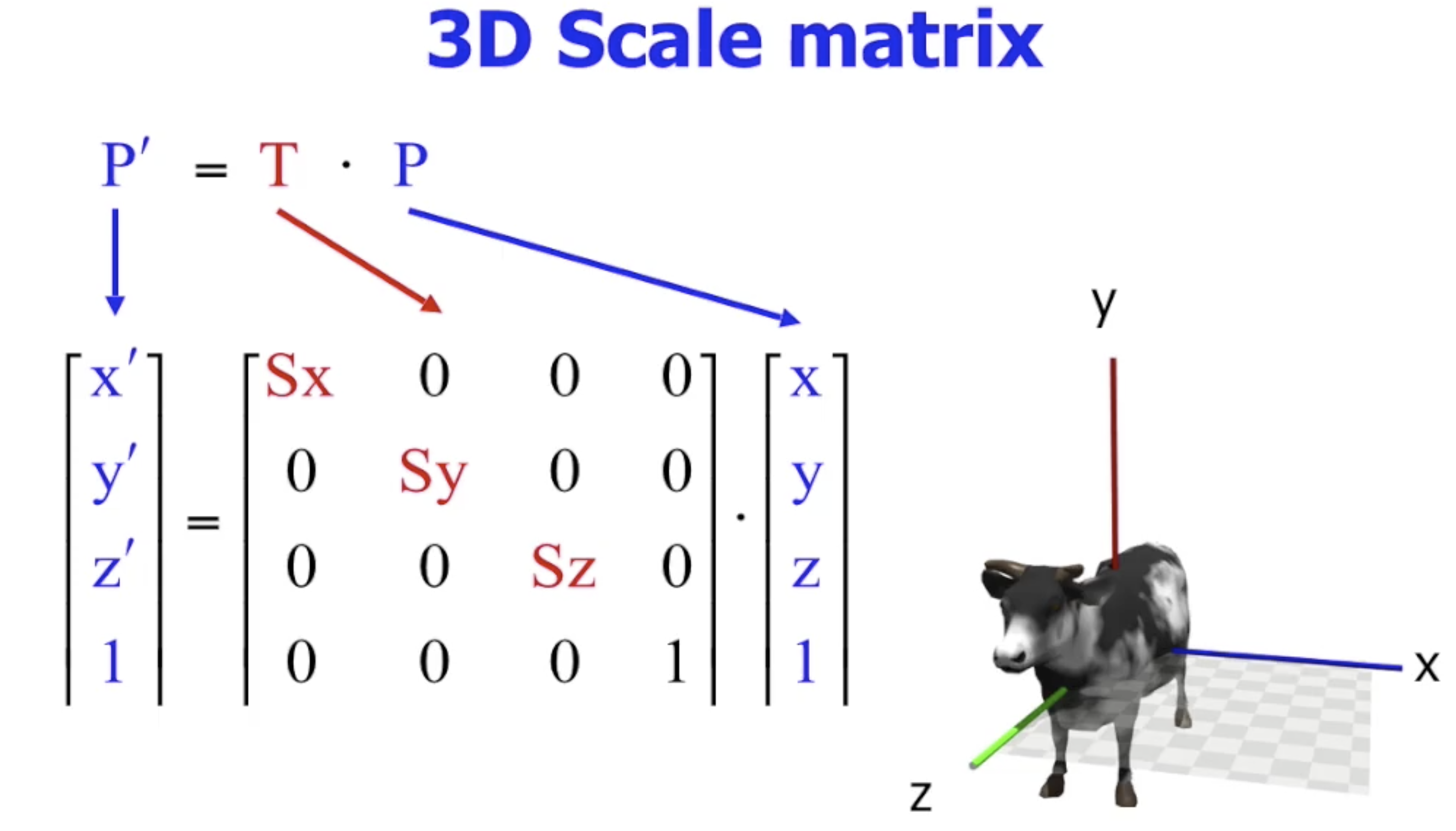
-
旋转矩阵
 $\uparrow$ 注意此处考虑的是 关于 $y$ 轴的夹角.
$\uparrow$ 注意此处考虑的是 关于 $y$ 轴的夹角.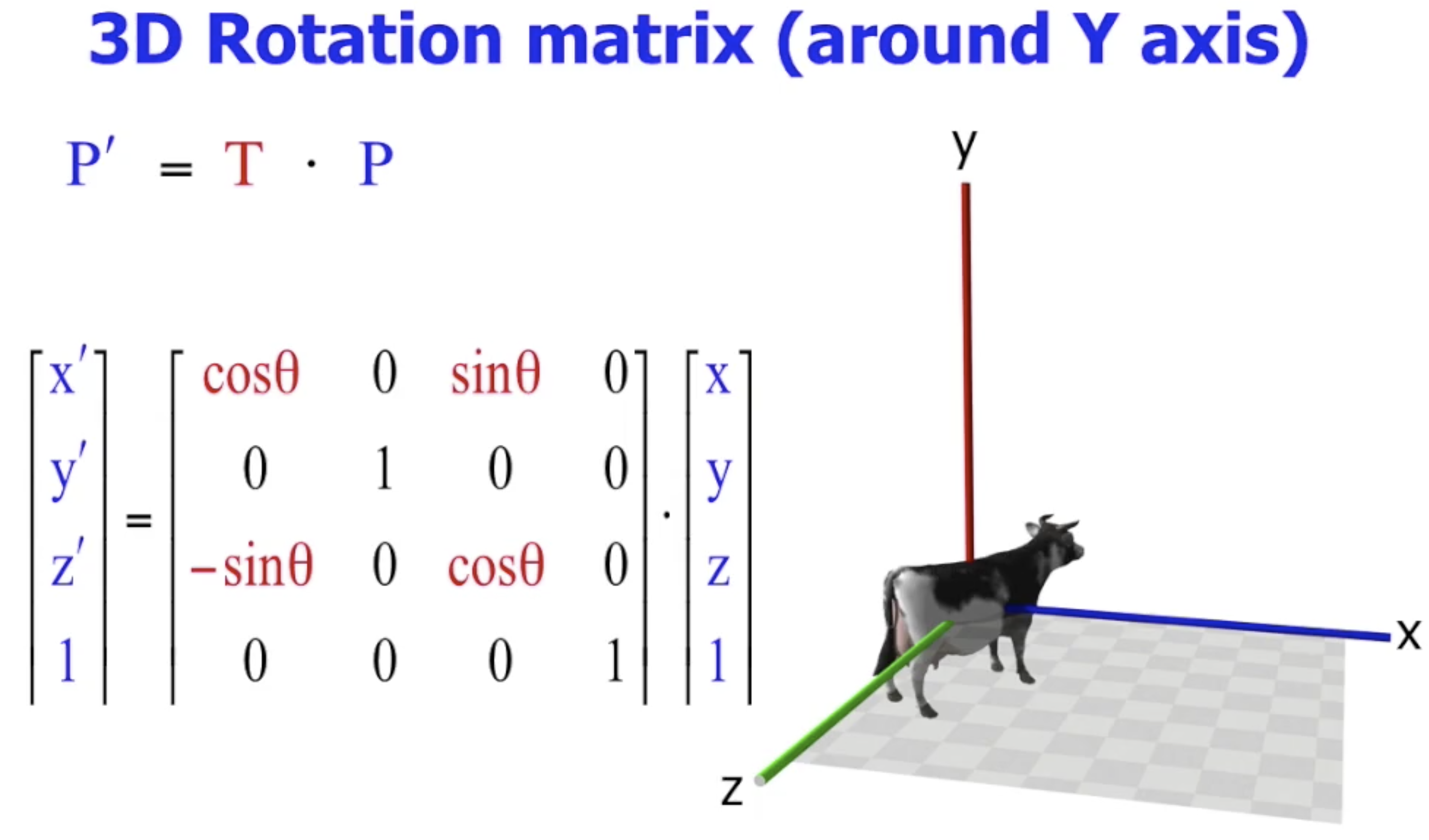
$\uparrow$ 注意此处考虑的是 关于 $z$ 轴的夹角.
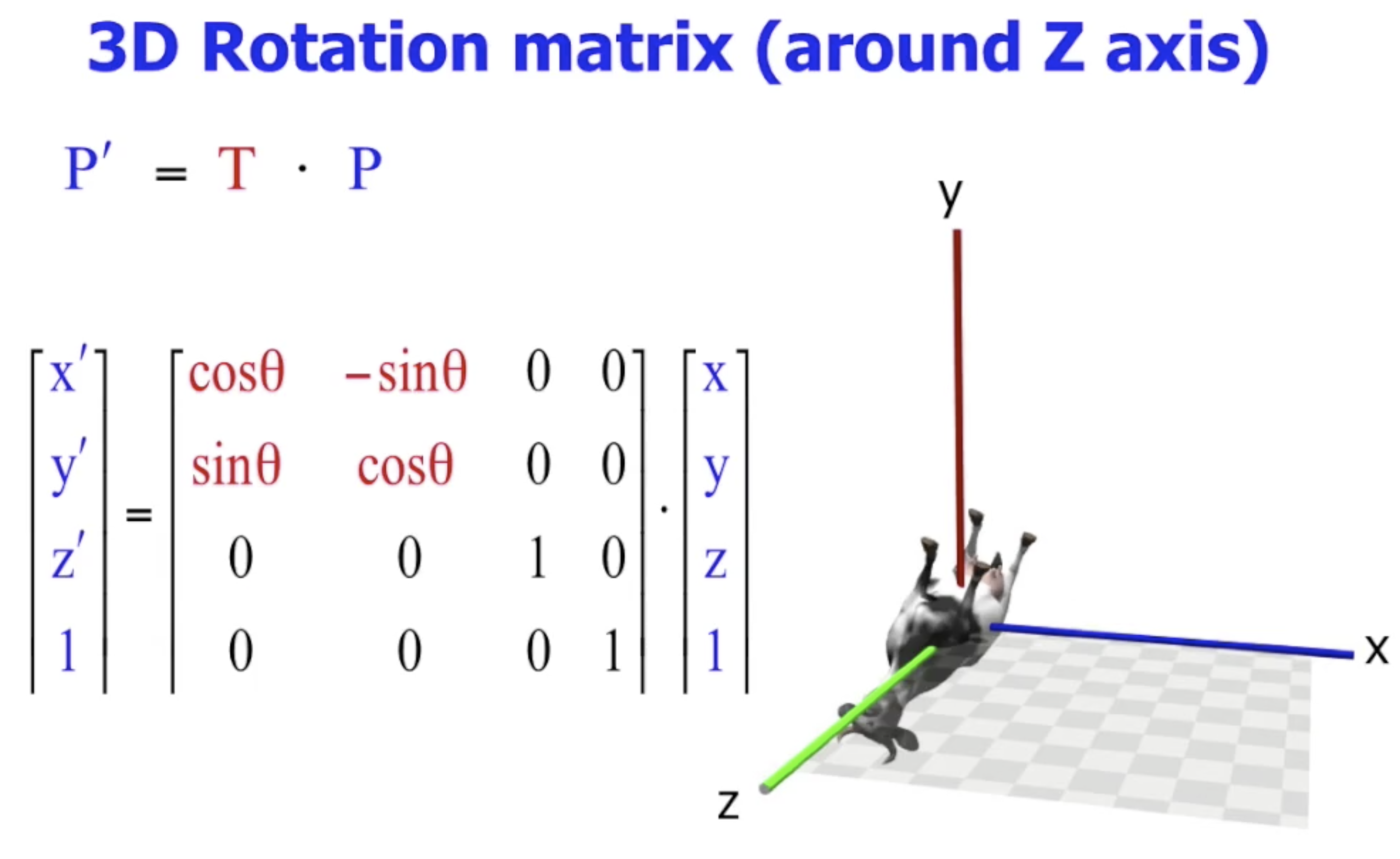
$\uparrow$ 注意此处考虑的是 关于 $x$ 轴的夹角.
-
平移矩阵
在上面一小节中我们已经引入了平移矩阵.
基于齐次坐标下的复合几何变换
这样, 通过引入齐次坐标我们就实现了不同几何变换的 统一化矩阵表示. 基于矩阵运算的基本知识可以立即想到, 复合几何变换的表示就是这一系列分变换对应矩阵的 依序乘积:

需要注意, 由于 矩阵乘法不满足交换律, 因此 不可用不匹配的矩阵乘法表示有序的几何变换流水线!
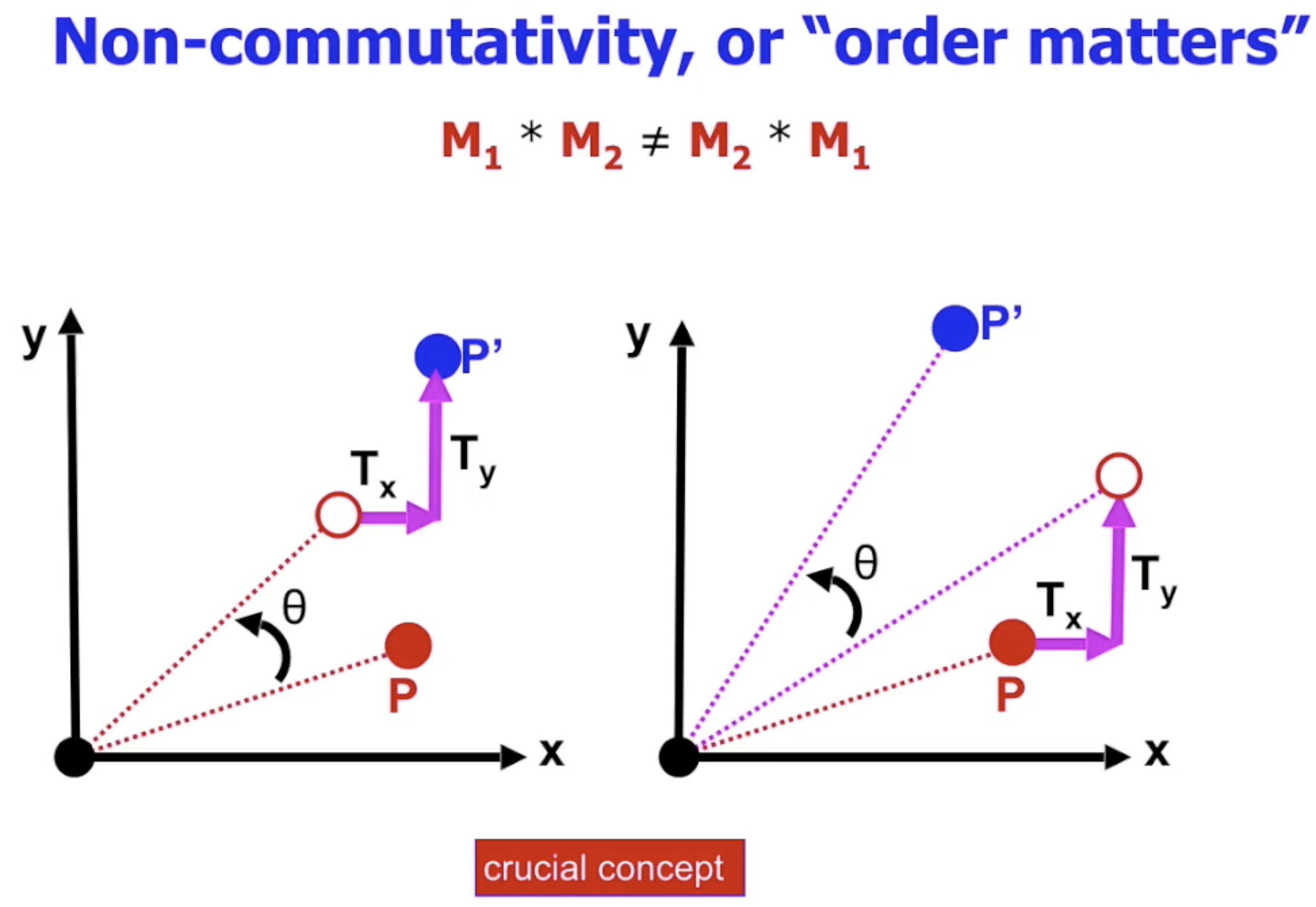
二维空间中的复合几何变换
举例而言, 考虑二维空间中的, 以某个不为 $(0, 0, 0)$ 的点为原点的缩放变换, 则需要:
- 构造将原点和目标对象 平移回原点 的平移操作矩阵 $M_1$
- 构造关于原点的缩放矩阵 $M_2$
- 构造对冲 $M_1$ 效果的反向平移矩阵 $M_3$
随后, 表示整个复合变换的矩阵就是 $M_3 \cdot M_2 \cdot M_1$.
(注意, 我们使用列向量表示点, 因此对点的几何变换实际上就是矩阵的 左乘.)

注意此处在矩阵运算的角度上看, $M_1$ 和 $M_3$ 互为 对方的逆矩阵:
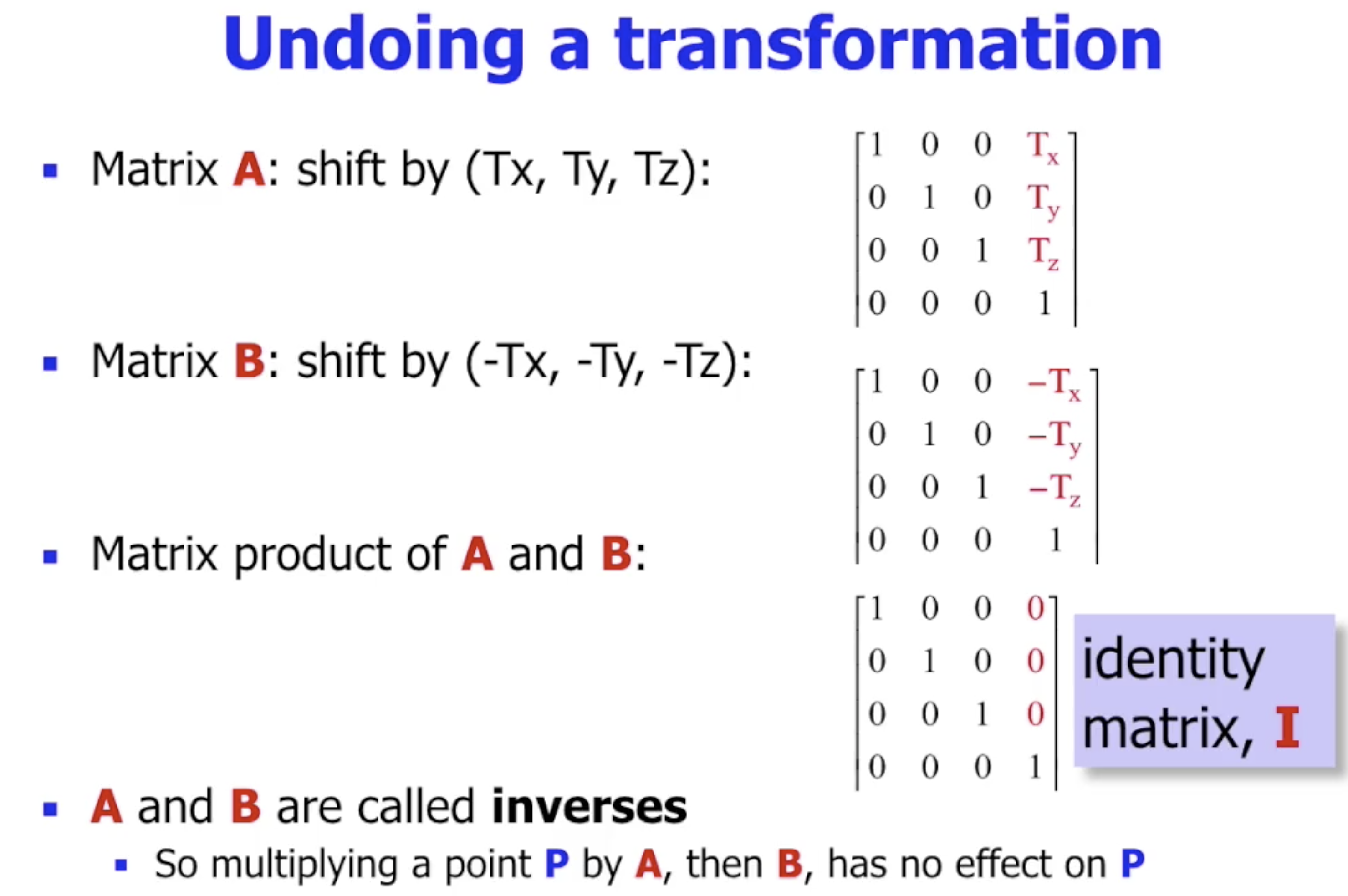
需要注意, 正如只有行列式不为 $0$ 的方阵才有逆矩阵 一样, 不是所有的变换都是可逆的!

比如考虑下面的 投影变换: 可以看出在投影过程中, 我们 永久丢失了一个维度上的深度信息, 因此显然由于丢失的信息不可找回, 这一变换自然也是不可逆的.
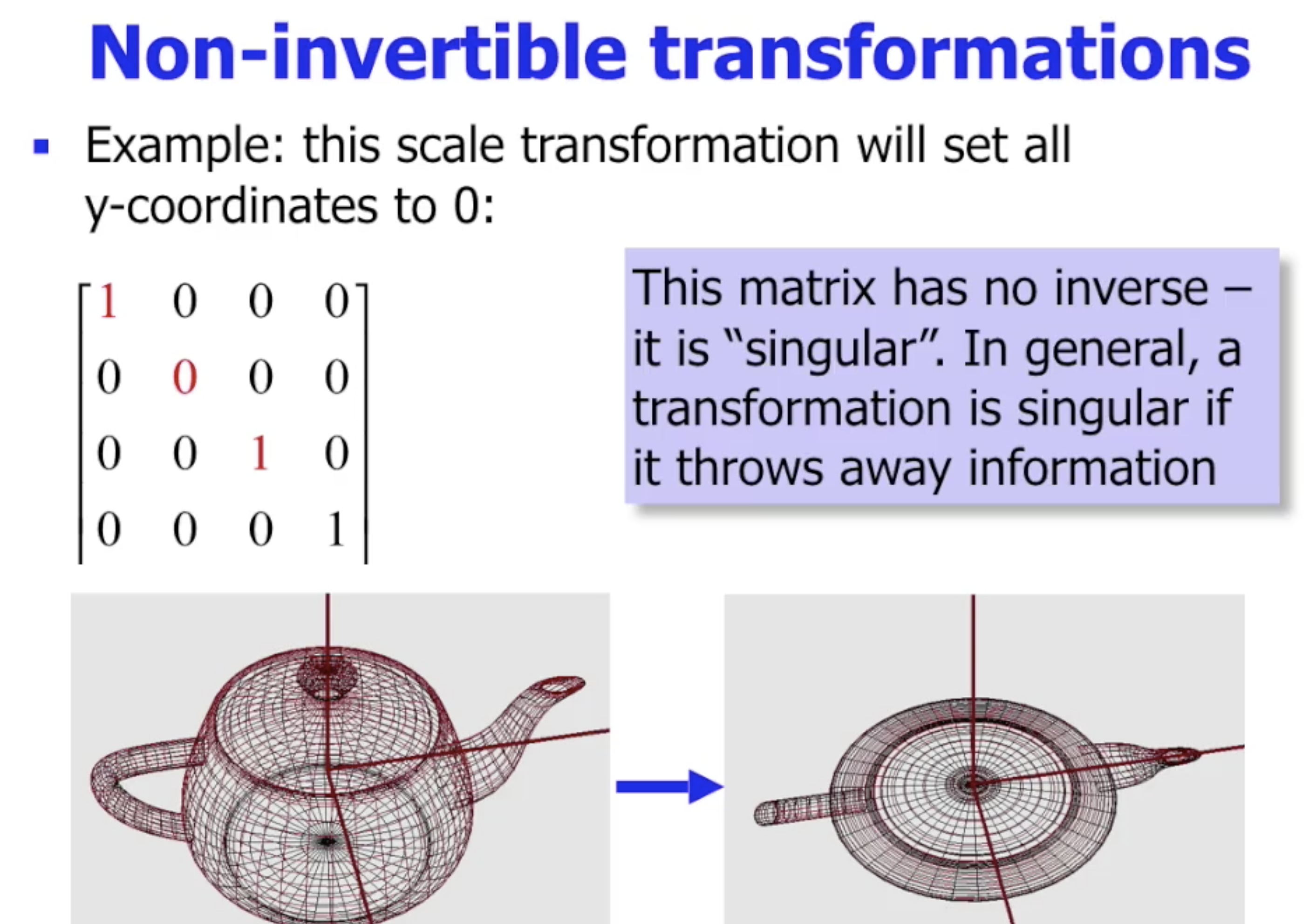
自然, 对应的矩阵表示的行列式也为 $0$. 我们称这样一类 在变换中抛弃信息 的变换为 Singular 的.
三维空间中的复合几何变换
最后考虑三维空间中的复合变换:
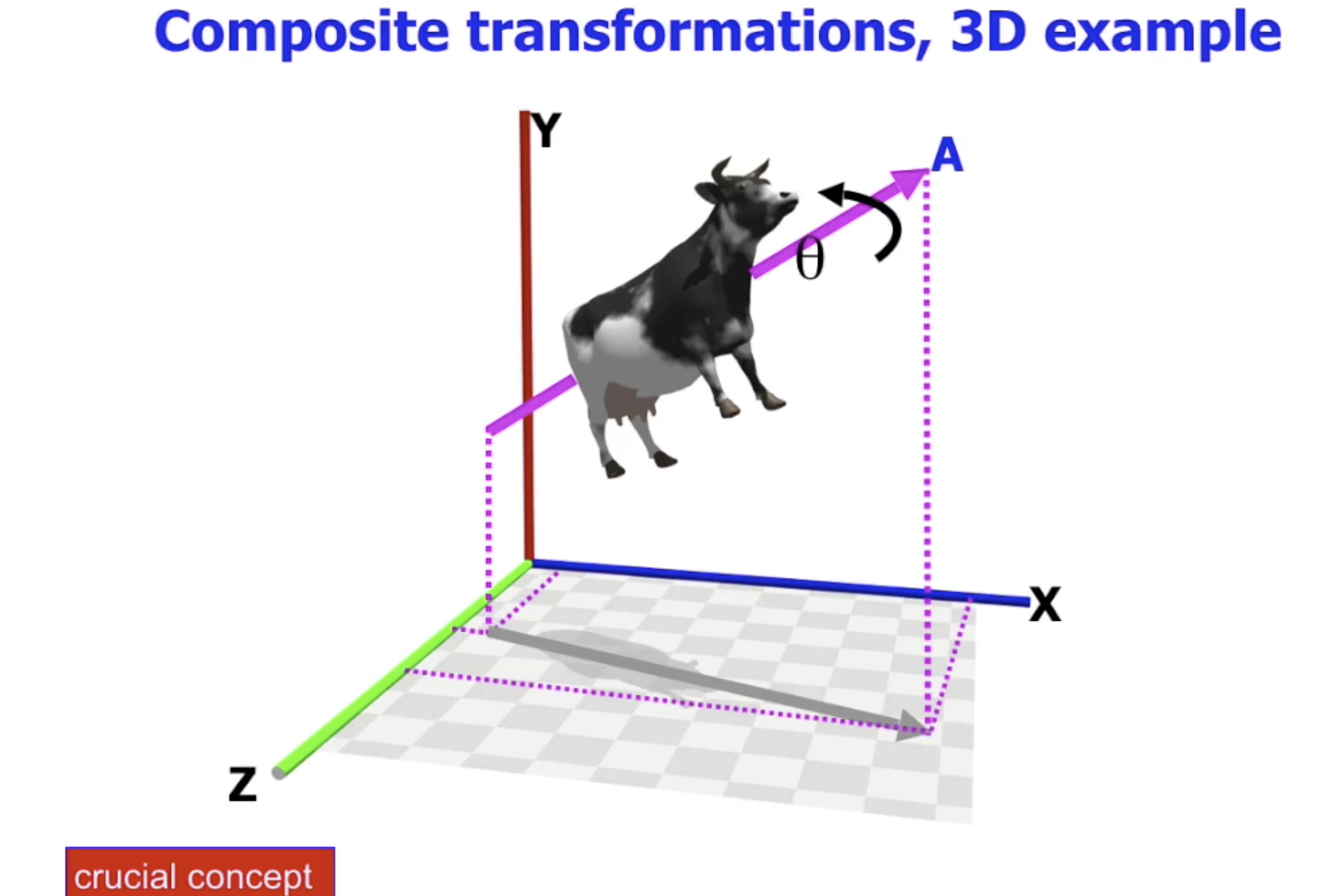
举例, 我们需要将上图中的几何图形关于向量 $A$ 旋转. 可以看出, 变换成本最低的方式自然是, 首先构造将向量 $A$ 转换为一个在 $X$ 轴上的向量的复合平移-旋转变换, 在执行 $y-z$ 轴上的旋转变换之后再反过来执行原来的复合平移-旋转变换.
由于对 $A$ 的复合平移-旋转变换过程中不损失信息 (Non-Singular), 因此这一操作是可行的.
下面考虑复合平移-旋转变换.
首先 沿 $z$ 轴负方向 平移 $A$, 直到其通过原点:
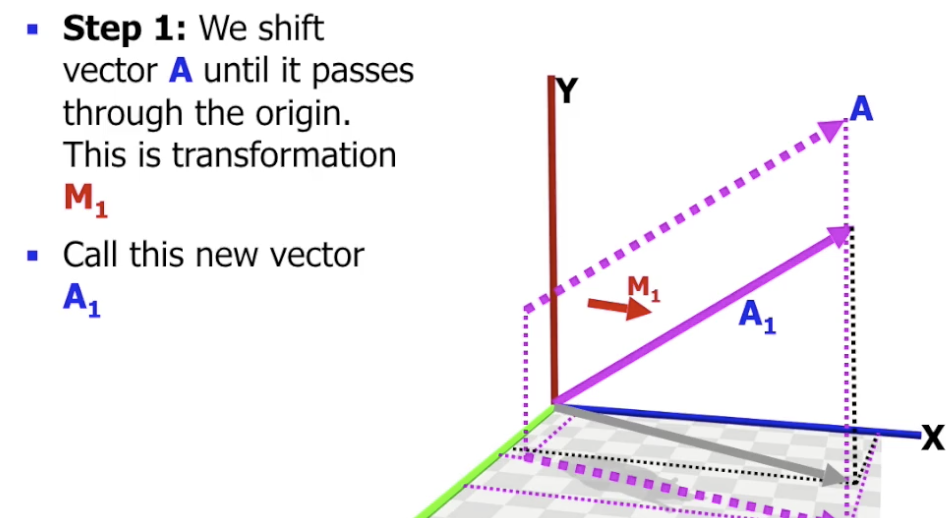
记该平移变换对应的矩阵为 $M_1$, 所得中间向量为 $A_1$.
其次在 $y-z$ 平面上执行顺时针旋转操作 (也就是 “Rotate A_1 about X axis”), 使 $A_1$ 位于 $x-y$ 平面上:
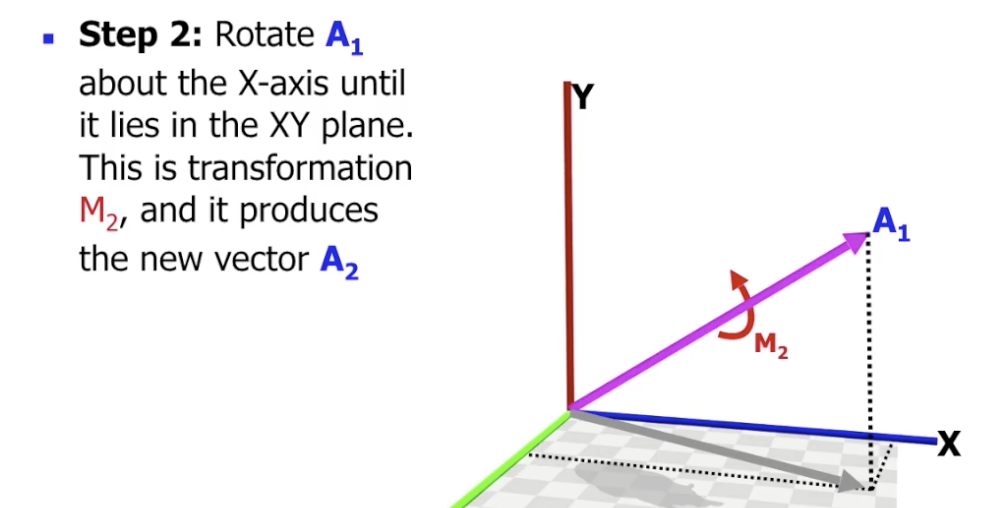
记该平移变换对应的矩阵为 $M_2$, 所得中间向量为 $A_2$.
最后在 $x-y$ 平面上执行顺时针旋转操作 (也就是 “Rotate A_2 about Z axis”), 使 $A_2$ 位于 $x$ 轴上:
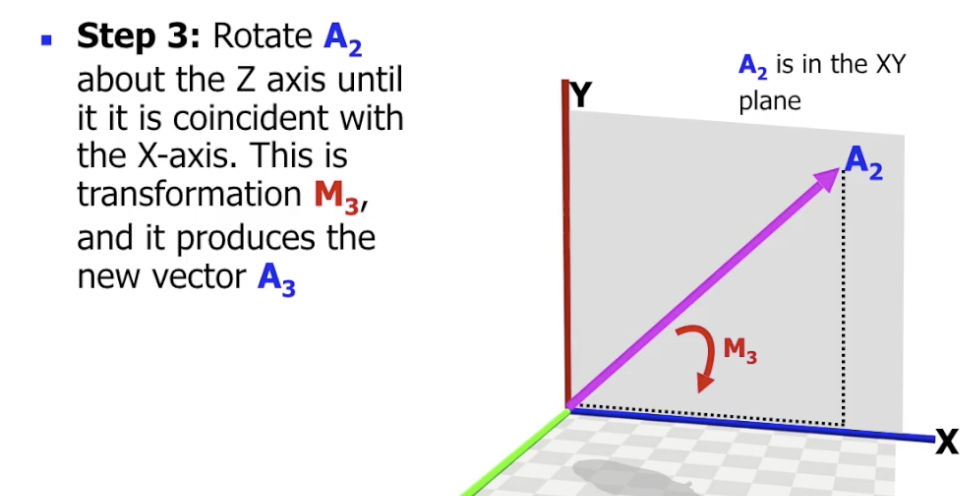
记该平移变换对应的矩阵为 $M_3$, 所得中间向量为 $A_3$.
此时复合平移-旋转变换完成, 复合矩阵为 $M_3 \cdot M_2 \cdot M_1$.
设在 $y-z$ 轴上的旋转变换矩阵为 $M_4$, 则整个变换的复合矩阵就是:
\[(M_3 \cdot M_2 \cdot M_1)^{-1} \cdot M_4\cdot M_3 \cdot M_2 \cdot M_1\]也就是下图所示的转化矩阵.

OpenGL 维护两个转换矩阵: Modelview Matrix 和 Projection Matrix, 前者控制图形本身的渲染变换, 后者控制图形如何被投影到视场 (屏幕) 上.

向量几何学的后备知识
此处只需注意 矢量叉乘 的定义:
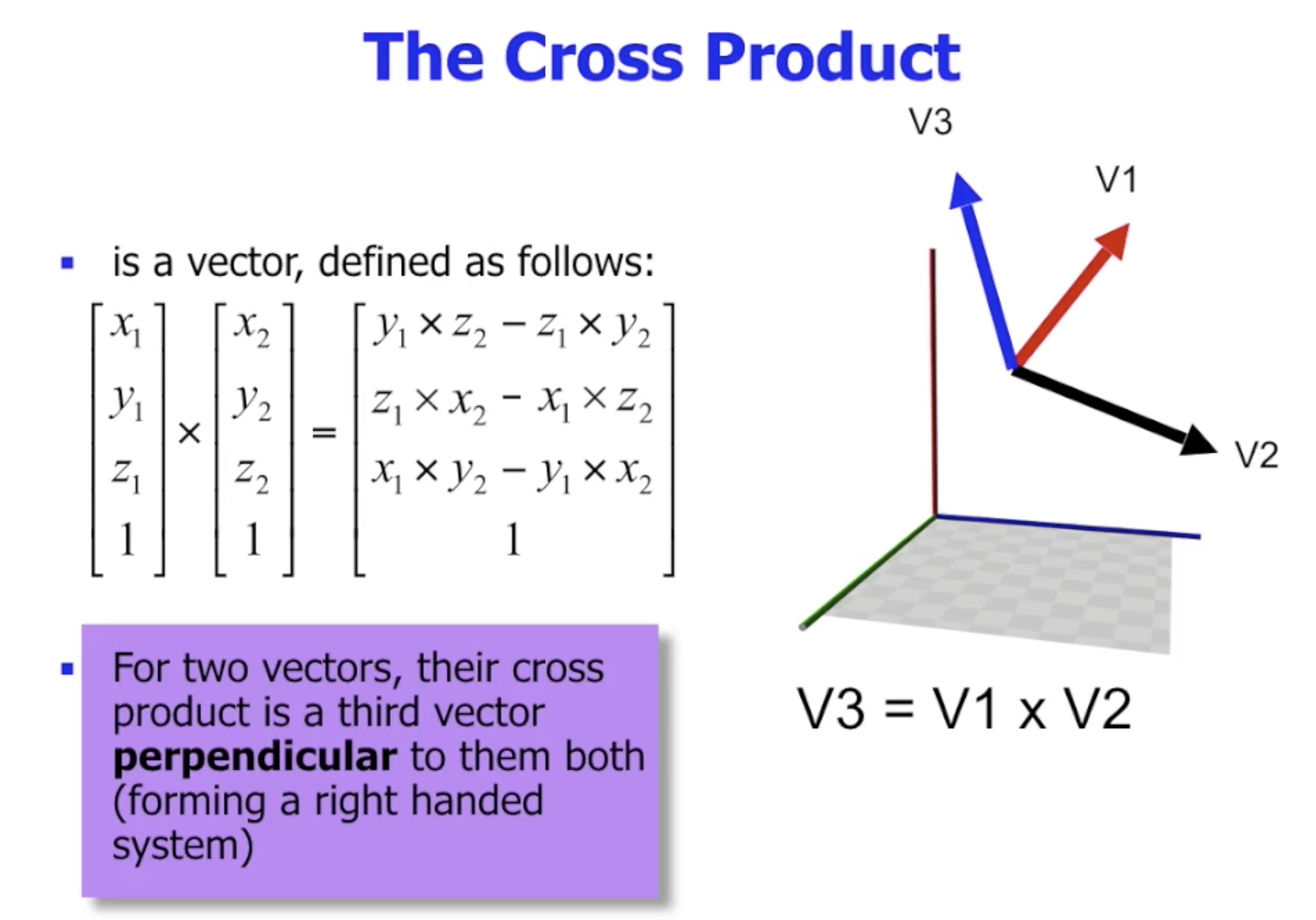
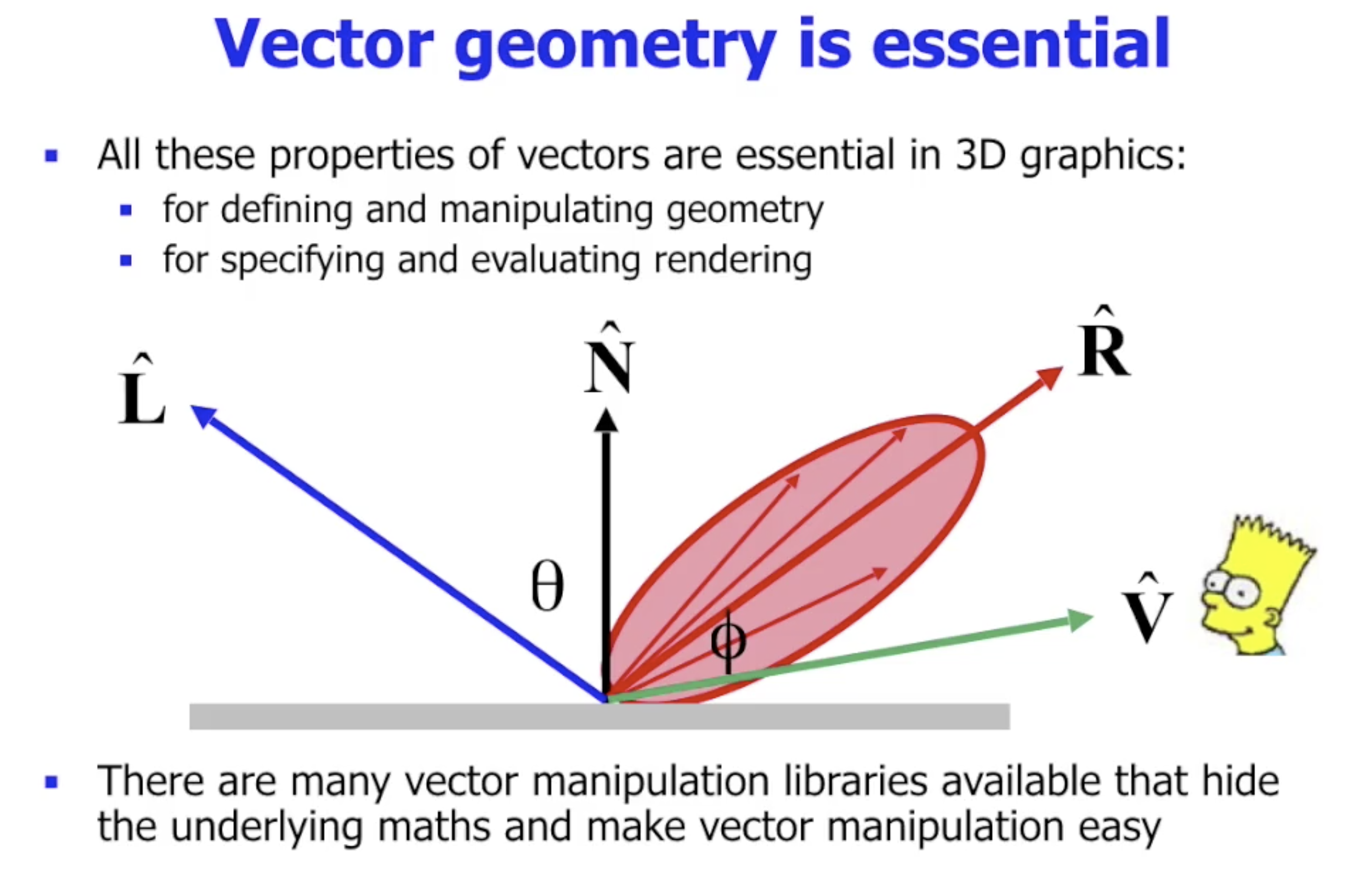
着色器
下面讨论图形管线的重要组成部分: 顶点着色器 和 片段着色器.
首先回顾图形管线的基本结构.
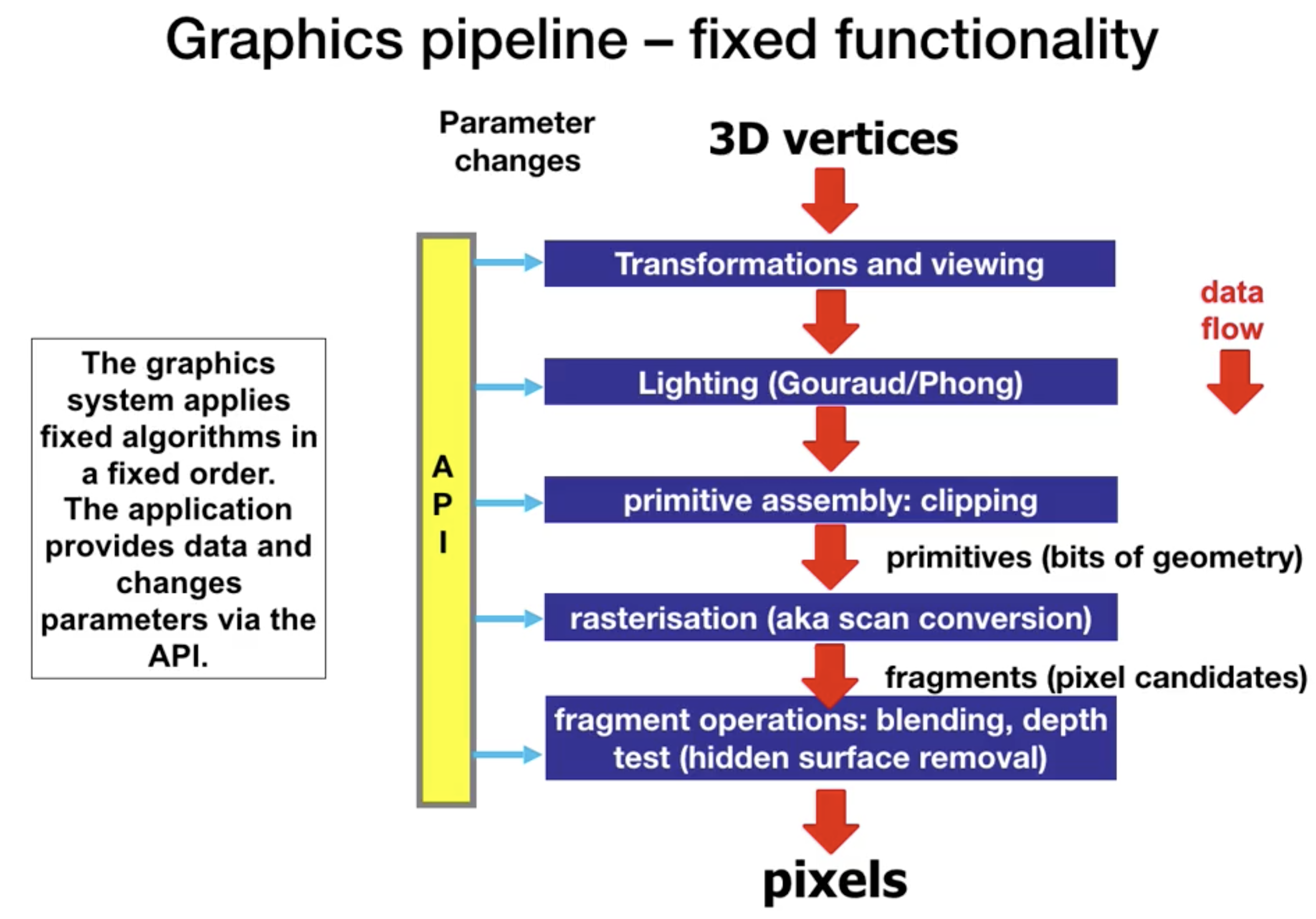
图形管线实质是一系列有序的, 由不同算法和处理流程组成的流水线, 它的行为受 API 传参的控制, 接收 3D vertices, 将其处理后输出像素, 信息在流水线不同层中单向流动.
而更先进的 可编程图形管线 支持用户自定义顶点着色器和片段着色器, 编写着色器的语言就是 GLSL (GL Shading Language). 需要注意, 着色器 不只分顶点着色器和片段着色器两种, 它们只是 最普通的着色器, 更高级的还有 几何着色器 (Geometry Shader) 和 细分曲面着色器 (tessellation Shader) 等.
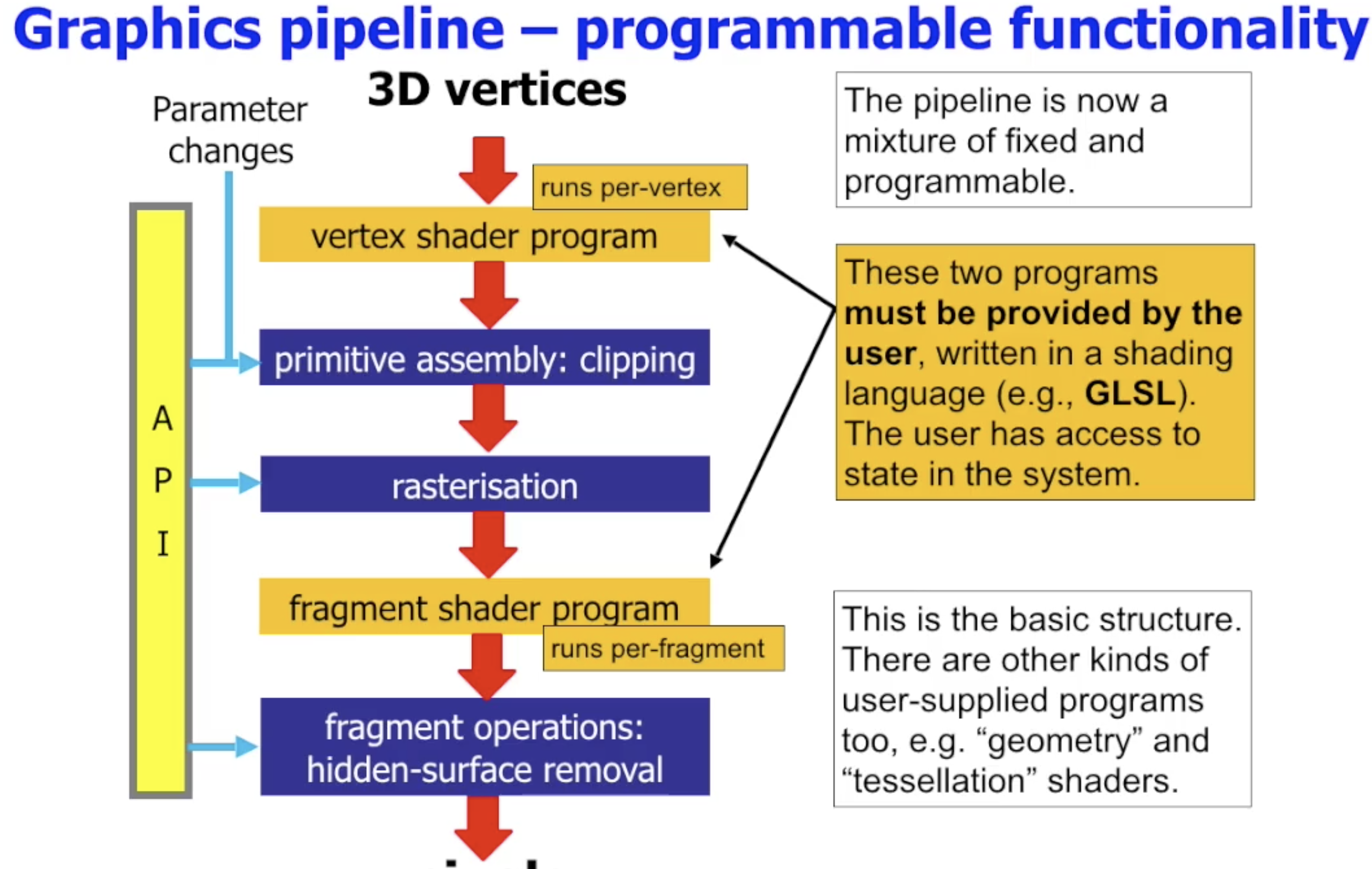
顶点着色器
我们再来讨论 顶点着色器. 首先明确, 所有的图形实际上都是由 顶点 组成的, 图形的边只不过是 顶点之间互相连通 的产物.
顶点着色器的任务 至少 是, 接收顶点 并对其进行一系列处理, 输出该顶点将在屏幕上显示的位置.
注意此处实际上顶点着色器的输出应该是一个 四维 的 齐次坐标, 而这个齐次坐标包含的信息 最终会作为这个顶点的片段着色器的输入, 我们将在后面详细讨论顶点着色器和片段着色器之间的信息传递.

顶点着色器的工作流程如下图所示, 基本上它同时接收图形的顶点信息和其他一同被传入的信息, 生成该顶点在屏幕上被渲染的位置.
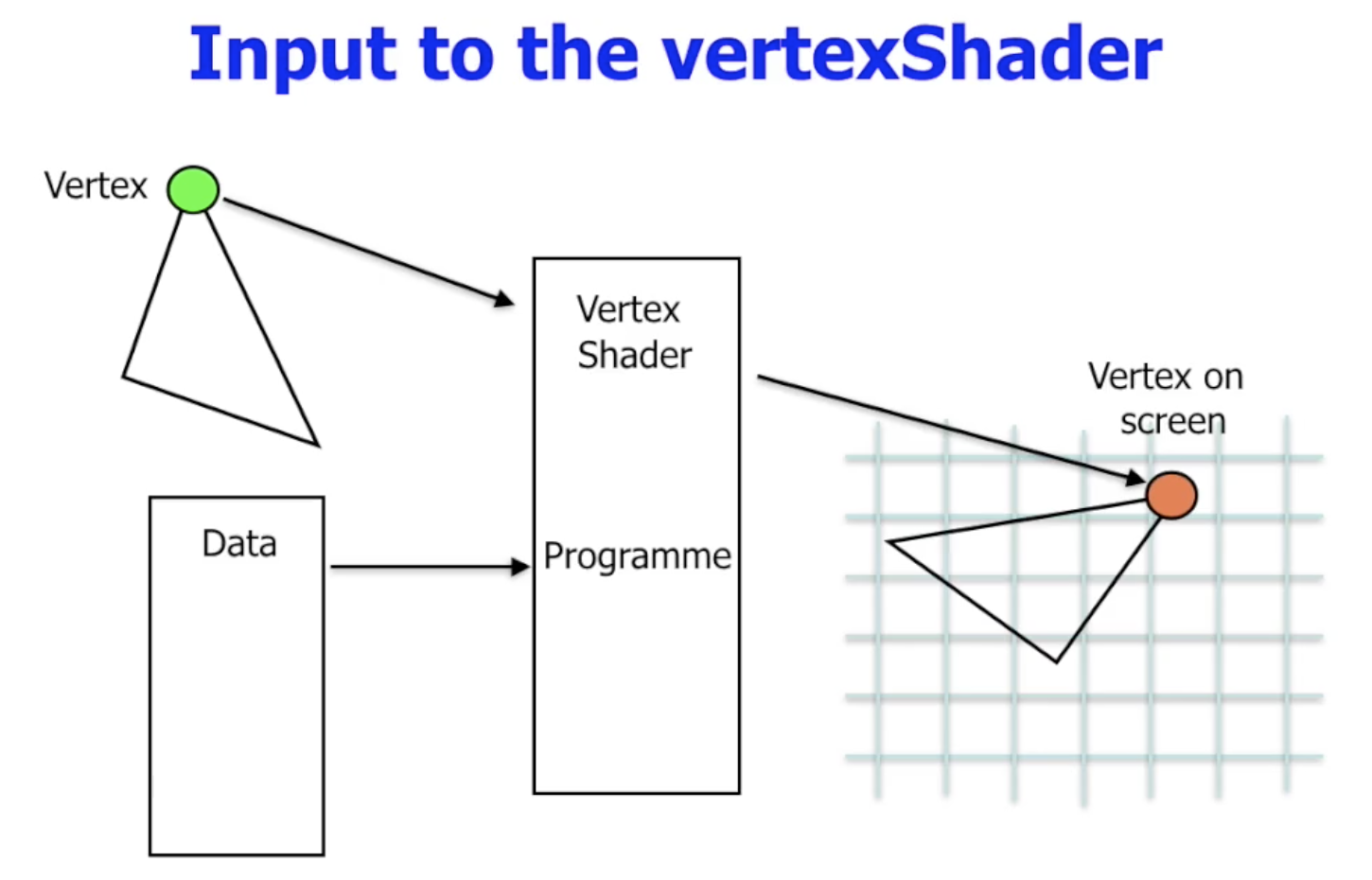
值得注意的是, 在 ThreeJS 中, 若我们不人为指定顶点着色器, 则它会自动创建默认顶点着色器. 我们还可以 单独为每一个顶点指定不同的着色器.
最简单的顶点着色器如下图所示:

注意此处的 “light data, vertex color, vertex normals, etc” 就是工作流程图中里和顶点一起被一同传入顶点着色器的 Data.
片段着色器
然后讨论 片段着色器:
顶点着色器解决的是 如何确定含有顶点的物体各个顶点在屏幕上渲染的位置 的问题, 而片段着色器解决的是 如何对含有顶点的物体上色 的问题.
因此, 和 “顶点着色器必须为 每个顶点 确定 位置: gl_position(a vec4)” 类似, 片段着色器需要为 每个片段 确定 gl_FragColor(a vec4), 这就是这个片段的 颜色.

片段着色器的工作流程如下图所示. 基本上它同时接收 片段中像素的位置信息 和 其他数据, 生成该像素的颜色.
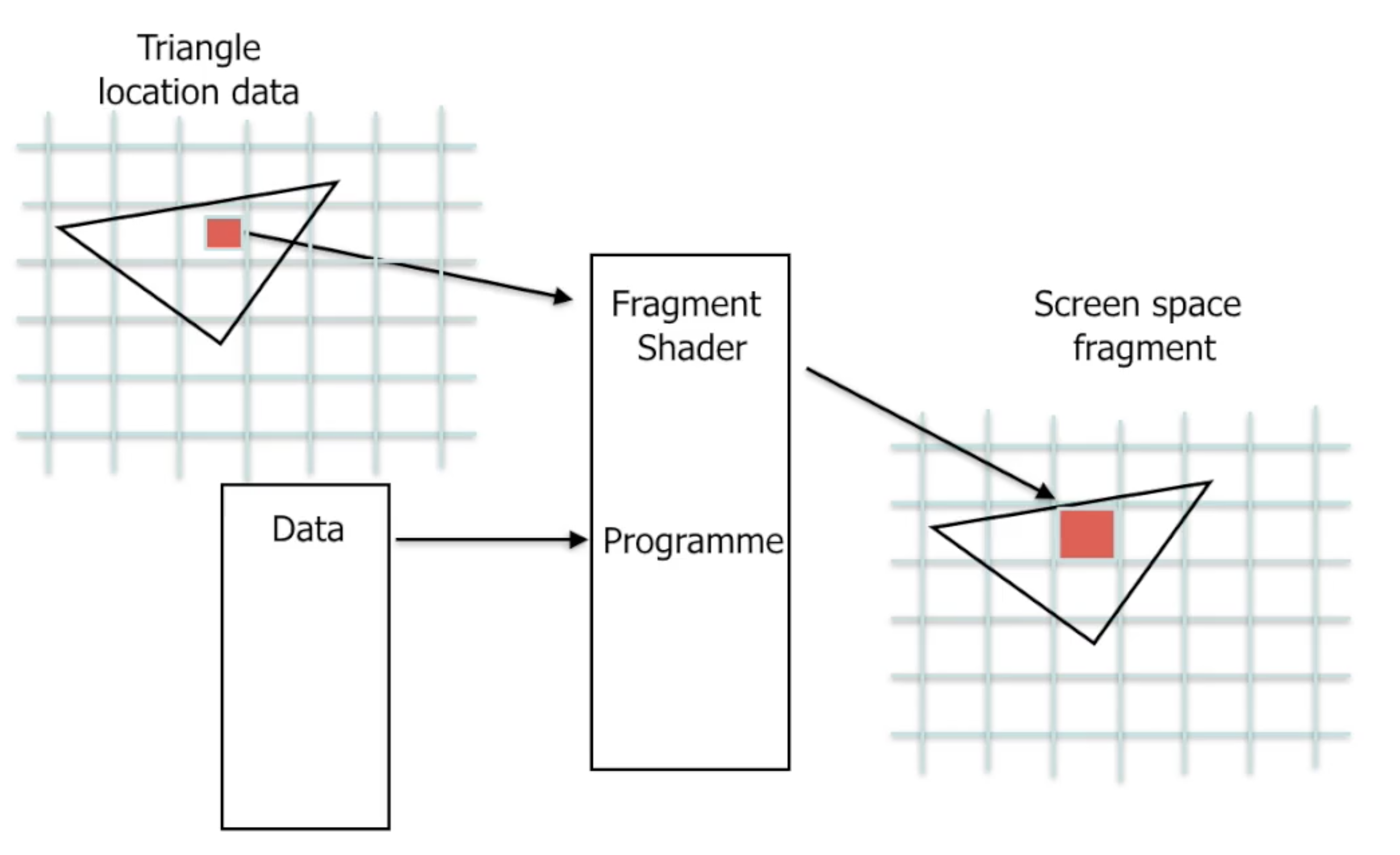
同样, 在 ThreeJS 中, 在未人为指定片段着色器时, 也会自动创建默认的片段着色器.
最简单的片段着色器如下图所示:

注意, 片段着色器需要和 mesh 结合.
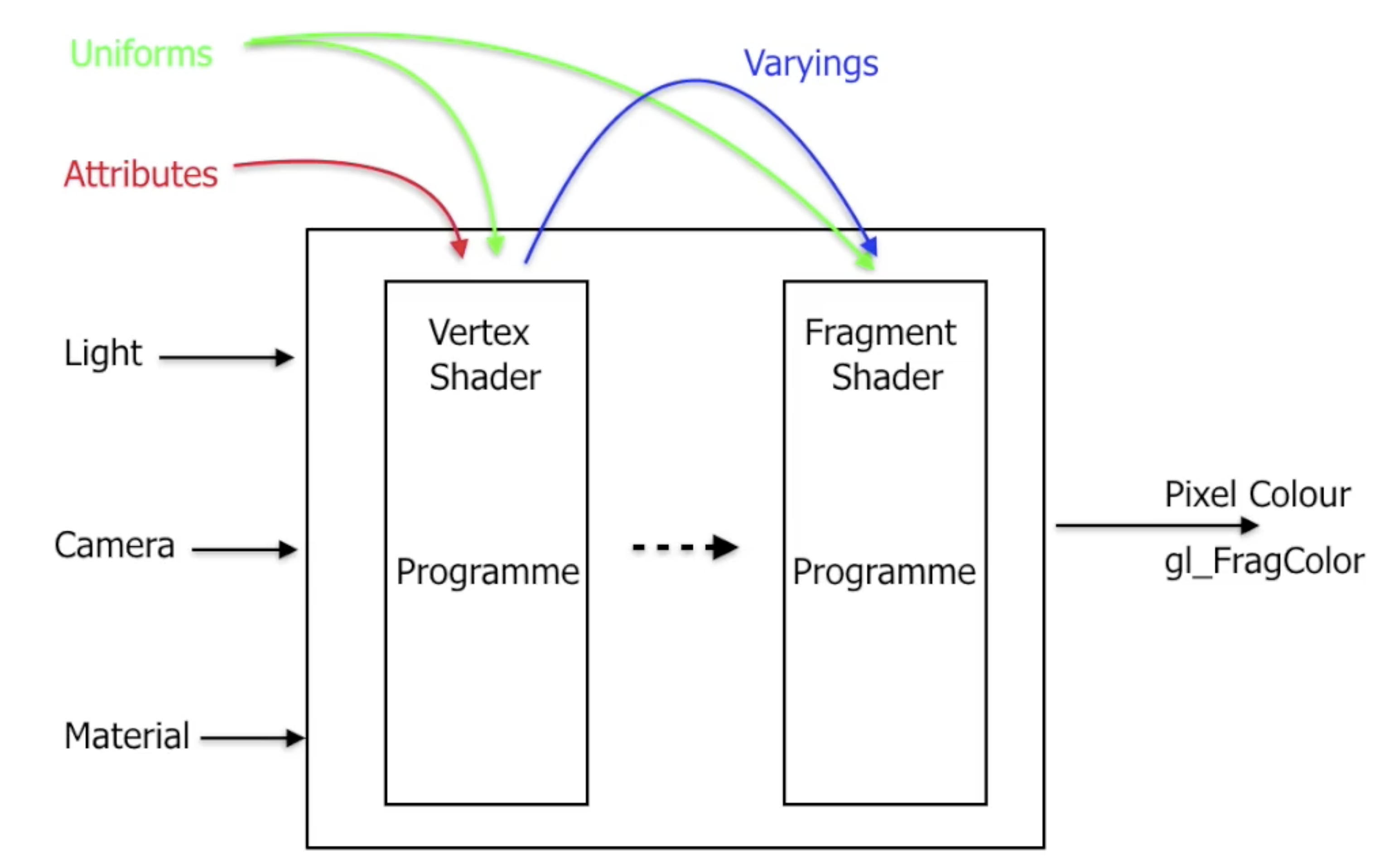
顶点着色器和片段着色器间的信息传递
在顶点着色器输出顶点的位置信息 gl_Position (一般表示为坐标) 后, 这些信息会经过包含 栅格化 等中间步骤最终生成 片段 (Fragments), 然后作为输入传到片段着色器中. 流程图如下所示:
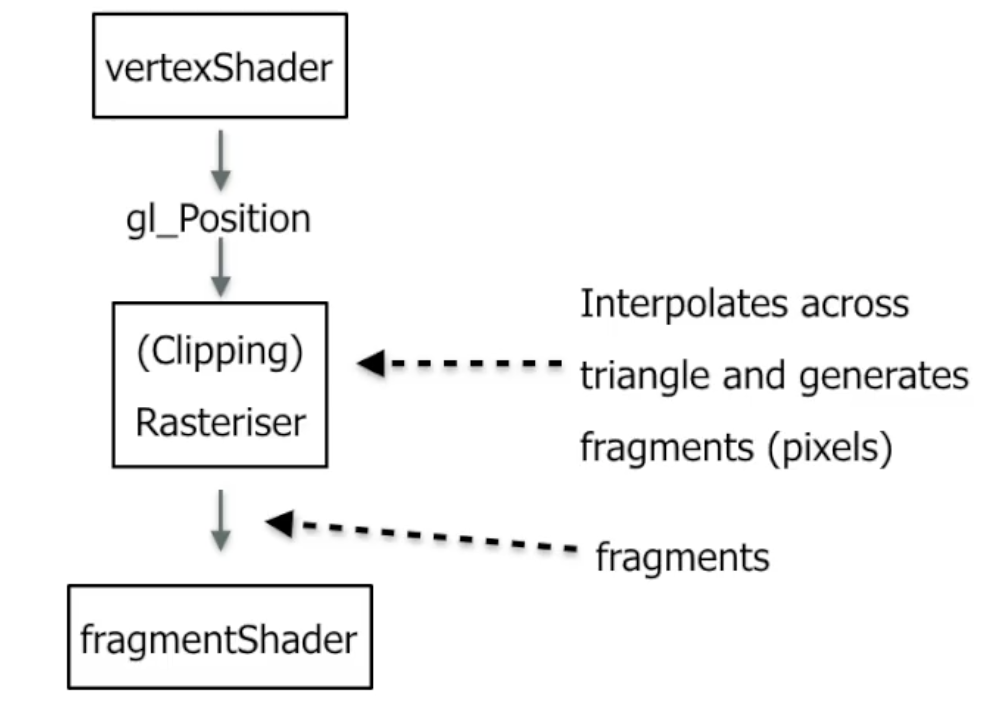
一般地, 在 GLSL 中向顶点着色器或/和片段着色器中传递信息的方式有下列三种:
-
Uniforms: 外部程序 传递给 (顶点和片段) 着色器的变量, 基本可以视为 常量, 任何类型的着色器都 只能用, 不能改. -
Attribute: 是 应用于单独顶点 且 只能在顶点着色器中使用 的变量, 我们无法在片段着色器中声明attribute类型的变量, 这样的变量也不能被片段着色器使用, 一般涌来表示顶点专有的数据, 如顶点坐标, 顶点颜色等. -
Varying: 用于执行顶点着色器和片段着色器之间的 数据传递, 一般通过作为 顶点着色器和片段着色器的共有变量 使用, 必须确保双方 (变量名和数据类型) 声明一致. (回顾COMP26020 Ch4 中并行计算中线程的概念), 注意这里和 线程 不同: 由于在图形管线中 数据单向地从顶点着色器向片段着色器流动, 因此对共用的Varying类型变量的修改 始终是顶点着色器先, 片段着色器后, 因此不存在资源竞争现象.