图遍历和拓扑排序
我们将在本章中引入 图 的概念, 介绍图遍历的基本技巧和拓扑排序.
1. 图
我们首先介绍图的基本定义和记法:
定义 1.1 (图)
图 (
Graph) 由 节点集 $V$ 和 边集 $E$ 组成, 并满足 $E \subseteq V \times V$, 即任何边的顶点都位于节点集中.一般地, 我们用数字标记每个节点, 且边集中的元素相应地表示为 $2$-元组. (顶点对).
若不考虑边集中顶点对的顺序, 则称该图为 无向图, 反之则称其为 有向图.
需要注意: 对有向图而言, 元组中元素的顺序表示边的指向: 从元组的第一个元素代表的顶点指向后一个顶点.

定义 1.2 (路径)
称 路径 (
\[u_1\cdots u_n\]Path) 为一系列节点 $u_1, \cdots, u_n$ 组成的序列且序列中任意相邻的两个节点在图中都通过边相连, 即: \(\forall \{1, \cdots, n-1\}, ~~ (u_i, u_{i+1}) \in E.\)
需要注意: 若未经特殊说明, 一律认为路径均为无圈的, 即路径中不存在重复节点.

定义 1.3 (环路, 圈)
称起始节点和终止节点相同的路径为 环路 或 圈 (
Cycle).
定义 1.4 (简单图)
称具备下列性质的图为 简单图 (
Simple Graph):
- 图中不存在任何平行的边, 即任何两条边的起始节点和终止节点都不完全相同.
- 图中不存在任何起始节点和终止节点相同的边.
定义 1.5 (子图, 生成子图)
图 $G = \langle V, E\rangle$ 的 子图 $G’ = \langle V’, E’\rangle$ 满足:
\[V' \subseteq V, ~ E' \subseteq E.\]若 $V’ = V$, 则称 $G’$ 为 生成子图 (
Spanning Subgraph).
我们下面考虑图结构的抽象数据类型所可能具备的运算:

图结构 ADT 的实现可以使用两种数据结构完成: 邻接列表 和 邻接矩阵.
1. 图的邻接列表实现
在使用邻接列表实现图时, 我们存储的信息是 图中每个节点的子节点列表:

可见, 这一实现将每个节点 映射到它全体后继子节点组成的列表中, 因此方法 succ(u) 的实现是直接的.
同时, 边 可表示为任何节点与其任一个后继子节点组成的有序元组:
\[E = \{(u, v) \vert v \in \text{succ}(u)\}.\]最后不难得出, 这种实现方式的存储空间复杂度为
\[O(\vert V \vert + \vert E \vert),\]这是因为我们需要维护 每个节点的后继节点列表, 因此有 $\vert V \vert$ 个列表; 而每个后继节点列表的长度恰好是每个列表所属节点延伸出的边的条数, 累加即得总数恰为 $\vert E \vert$. $\blacksquare$
因此不难得出该实现下对应运算的时间复杂度:

2. 图的邻接矩阵实现
在使用邻接矩阵实现图时, 我们存储的信息是图中 任意两个顶点之间的连接状态:
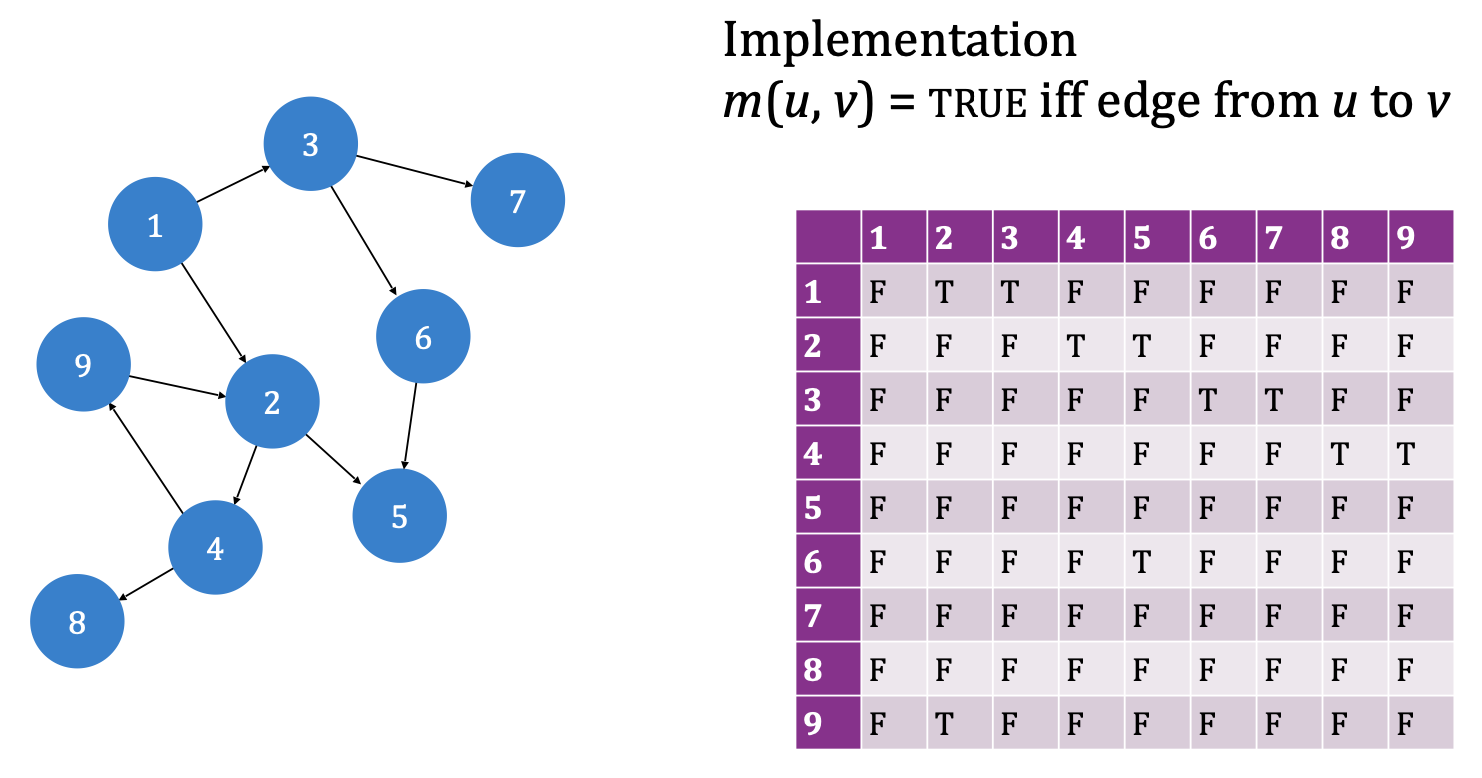
可见任何与 Edge 相关的运算的实现都是直接的. 这一实现的存储空间复杂度显然为
$O(\vert V \vert^2),$
不适合较稀疏, 即 $\vert E\vert « \vert V \vert ^2$ 的图, 因为在该情况下空间利用率极低.
而邻接矩阵实现的优越性也是显而易见的: 由于它直接存储了图的边信息, 因此和边相关的任何运算时间复杂度均为 $O(1)$:

由此可见, 图 ADT 的两种实现各有利弊. 图的邻接列表实现对空间的要求低, 且在查询后继节点时运算时间复杂度为 $O(1)$; 而图的邻接矩阵实现对任何涉及边的运算的时间复杂度都具有无与伦比的优越性, 但对存储空间要求较高. 对于具体问题而言, 如何选择图 ADT 的实现还需基于需求具体分析.
2. 图遍历
本节我们讨论 图遍历. 和树遍历不同, 图遍历的真实含义并非遍历某条路径, 而是 遍历整个图: 访问图的所有节点. 我们下面介绍三种图遍历算法: 通用算法 (Generic), 深度优先和广度优先.
2.1 通用算法
通用算法遵循的原则是: 通过不断访问边从而探索新的节点, 直到所有的节点都被访问过至少一次为止. 为了达成这一目标, 算法需要维护两个 List 分别存储:
- $F$: 已经遍历过的边.
- $D$: 已经发现但尚未检查以它为出发点的边的节点.
其伪代码如下:

下面讨论通用算法的正确性:
可见: 由于我们是从 $s$ 开始遍历图, 因此在该过程中通过遍历所发现的所有节点都是可以在图中从 $s$ 出发到达的 (Reachable). 即:
任何位于集合 $D \cup F$ 中的节点都是可达的. 在最初始状态下, $D \cup F = {s}$. 而在遍历过程中, 只有 $D \cup F$ 中元素的后继节点才会被加入到该列表中.
同时可知, 若图中的某个节点是可达的, 则它必被包含在边集 $F$ 内的某个元组中.
因此, 在通用算法完成对图的遍历时, 图中任意可达的节点都已经沿着以 $s$ 为出发点的某条路径被遍历过.
2.2 深度优先与广度优先算法
通过分别将通用算法中存储待检索节点的数组视为栈 (后进先出) 或堆 (先进先出), 就可以将其转化为图遍历的 广度优先算法 和 深度优先算法. 广度优先与深度优先算法的实质差异在于, 我们在检索到某个节点的所有子节点后, 是选择进一步优先遍历它的子节点, 还是选择先完成该节点的同级节点的遍历, 对优先级的控制是通过调整所发现的子节点被插入到数组中的位置来实现的.

值得注意的是, 我们还可以递归地实现深度优先算法:

此處注意:
- 求解深度優先和廣度優先時, 務必不要想當然, 而是 嚴格構造
Discovered棧/隊列 和Finished列表, 一步步地進行推導! - 對於深度優先算法, 若從
Discovered中彈出某個節點, 檢索其子節點中有Discovered中元素時, 須將Discovered中對於元素刪除, 然後再按照順序插入.
3. 拓扑排序
本节中我们简述拓扑排序的基本原理.
拓扑排序用于解决具备下列特征的问题:
- 存在一系列任务, 需要以合适的方式排序从而生成一个可供规划的任务执行顺序.
- 这一系列任务之间存在依赖关系, 即: 某些任务是其他一些任务的前束条件, 只有在执行它后才能进一步执行其他的任务.
- 任务之间的关系可被建模为有向图: 任务之间的依赖关系可用有向边表示.
拓扑排序的基本原理是:
将图中所有节点按照先后顺序排序, 确保没有从后往前指向的边.
需要注意, 拓扑排序只适用于有向无圈图 (DAG). 要实现拓扑排序, 我们首先需要对图进行检测, 确保它是无圈的, 然后再去实现基于深度优先的节点排序. 拓扑排序 不适用于有圈图.
我们首先讨论圈检测算法:
我们知道, 若某个路径的起始节点和终止节点重合 (相同), 则该路径构成了圈, 而检查给定的图是否为含圈图可以被转化为: 检查图中每一条路径是否都不是圈. 因此, 我们可以基于下列的原则构造算法:
- 首先将图中的所有节点标记为 $N$ (
New). - 在检索图时, 若首次遇到了某个节点 $n$, 则将其标记为 $O$ (
Open). - 因此, 在遍历过程中只要发现遇到了任何标记为 $O$ 的节点, 则这条路径一定是圈.
- 只有在遍历完它的全部子节点后, 才将其标记为已完成遍历的节点 $D$ (
Done).
在完成圈检测后, 我们需要对图进行拓扑排序. 而拓扑排序实际上可以被无缝集成至圈检测的过程中.
由于拓扑排序的原则是: “作为其他某些节点的前束条件的节点始终排在更前面”, 而在进行圈检测时任何情况下先被标记为 $D$ (Done) 的节点一定是更先被作为路径起始被考虑的节点, 即其他节点的前束节点.
因此, 只需要在某个子节点被标记为 $D$ (Done) 时, 将其插入结果列表的列表头中, 即可在圈检测结束后得到该图的 反向拓扑排序; 若将其插入结果列表的列表尾, 就得到了图的 拓扑排序. $\blacksquare$
最后以第一周最后一个视频中的例子收尾:
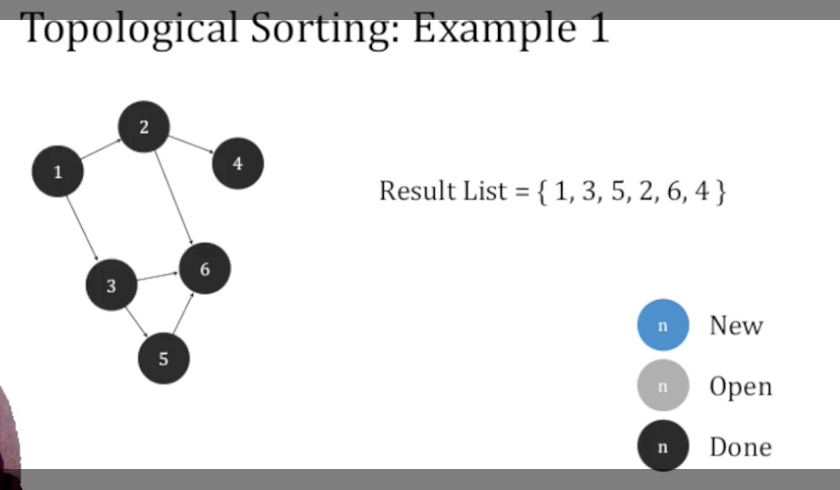
首先 优先遍历编号更小的点, 可知最先被发现没有任何子节点, 完成遍历的是 $4$, 其次是 $6$, 再然后是 $2$. $2$ 遍历完之后去遍历 $3$ 这个分支, 先完成 $5$ 的遍历之后尝试遍历 $6$, 发现 $6$ 已经是 Done 了, 所以返回 $3$, 最后返回 $1$.
