绪论

本质上我们将在本课程中所接触的内容是对智能体 (Intelligent System) 表示和推理其所在世界中的知识和信息的研究. 在本课程中, 我们将接触和学习 知识表示 (Knowledge Representation) 的核心概念和数种自动推理 (Automated Reasoning) 方法.

课程内容基本分为四个板块:

1. 一阶逻辑 (First-Order Logic) 和自动推理

• 一阶逻辑的 语法和语义
• 一节逻辑公式和子句形式 (Clausal Form) 的转换
• 有序语义归结 (Ordered Resolution)
• 基于饱和原则的证明搜索
• 模型 (Model) 构造

2. Prolog

• Prolog 语法和证明搜索执行规则
• Prolog 中基于 Horn 子句的反向链式推理法的应用
• 基于 Prolog 的定理证明

3. 知识表示

• 本体论工程 (Ontological Engineering)
• 对类型和物体的表示
• 对事件的表示
• 基于分类 (Categories) 的推理系统
• 语义网络 (Semantic Networks)
• 描述逻辑
• 基于默认信息 (Default Information) 的推理

4. 归纳推理与回溯推理

• 基于逻辑问题的学习 (Learning as a Logical Problem)
• 基于知识的学习 (Learning with Knowledge)
• 归纳逻辑程序设计
• 解释和诊断 (Explaination and Diagnosis)
• 基于解释的学习 (Explaination-based Learning)

我们下面开始对课程内容的介绍.

一阶逻辑 (First-Order Logic) 和自动推理

1. 基于一阶逻辑的知识表示

定义 1.1 (知识表示)

称 精确 (Precise) 和 无歧义 (Unambiguous) 的, 表示世界中的已知信息的方式为 知识表示.

定义 1.2 (自动推理)

自动推理一般被定义为 自动地 基于某些已知事实推导出与之相关的声明 (Statement) 的行为.

在一阶逻辑中, 推理是基于预先定义好的 推断规则 (Inference Rules) 执行的.

推理同样依赖于对现实世界中知识的表示以及所具有的知识的多寡. 对于一阶逻辑, 我们将知识库 (Knowledge Base) 视为对现实世界的 符号化抽象 (Symbolic Abstraction): 在知识库中, 称我们所关心的, 某个形式化的, 现实世界的子集为 域 (Domain), 而用于表示域中元素的符号为 标识 (Signature).

1.1 一阶逻辑的语法

定义 1.1.1 (标识, Signature)

称某个一阶公式的 标识

\[\Sigma = \langle \mathcal{F}, \mathcal{P}, \text{arr}\rangle\]

由两个不相交的, 分别包含 函数符号 与 谓词符号 的集合 $\mathcal{F}, \mathcal{P}$ 以及 表明每一个符号的元数 (Arity) 的映射

\[\text{arr}: \mathcal{F} \cup \mathcal{P} \rightarrow \mathbb{N}_0\]

组成.

定义 1.1.2 (项, Term)

在一阶逻辑中, 下列元素均称为 项:

1. 任何 变量 均为项.
2. 任何 常量 (即元数为 $0$ 的函数符号) 均为项.

3. 若函数符号 $f$ 的元数为 $k$, $k > 0$ 且 $t_i, i\in [k]$ 均为项, 则 \(f(t_1, \cdots, t_k)\)

   为项.

定义 1.1.3 (原子, Atom)

在一阶逻辑中, 下列元素均称为 原子:

1. 任何 谓词 (即元数为 $0$ 的谓词符号) 均为原子.
2. 若 $t_1, t_2$ 均为项, 则 $t_1 = t_2$ 为原子.

3. 若谓词符号 $p$ 的元数为 $k$, $k > 0$ 且 $t_i, i\in [k]$ 均为项, 则 \(p(t_1, \cdots, t_k)\)

   为原子.

定义 1.1.4 (公式 Formula)

在一阶逻辑中, 我们使用如下的规则递归定义 公式:

1. 任何原子均为公式.
2. 布尔值 True 为公式.

3. 若 $\phi_1, \phi_2$ 均为公式, 则 \(\neg \phi_1, \phi_1 \wedge \phi_2, \forall x. \phi_1\)

   为公式, 其中 $x$ 为变量.

进一步地, 我们可以定义:

1. $\text{False} \equiv \neg\text{True}$
2. $\phi_1 \vee \phi_2 \equiv \neg (\phi_1 \wedge \phi_2)$
3. $\phi_1 \rightarrow \phi_2 \equiv \neg \phi_1 \vee \phi_2$
4. $\phi_1 \leftrightarrow \phi_2 \equiv ((\phi_1 \rightarrow \phi_2) \wedge (\phi_2 \rightarrow \phi_1))$
5. $\exists x. \phi \equiv \neg(\forall x. \neg \phi)$.

我们可以不甚严谨地理解上述的逻辑符号或量词:

同时考虑如下的例子:

在一阶逻辑中我们可以使用下列的两种记法表示 函数:

1. 对于定义域有限的函数, 可以使用集合表示法.如:

   \[\{(1,2), (2,1)\}\]

   就表示了一个定义在 ${1, 2}$ 上, 将 $1$ 映射到 $2$, $2$ 映射到 $1$ 的函数.

2. 对于无法列举定义域中所有元素的函数, 可以使用 $\lambda-$ 抽象表示法: 使用

   \[\lambda x. (\text{expression using} ~x)\]

   表示以 $x$ 为输入, 以某个表达式为输出的匿名函数.

1.2 一阶逻辑的语义

我们将在直观简述一阶逻辑的语义后给出正规的形式化定义.

首先地, 项 一般用于表示某个 物体 (Object), 并且项无需是唯一的.

公式 用来表示某个声明具有真值, 它既可以是对某个既定现实的陈述, 也可以表示某个未经证实的, 将要被检验的声明.

符号 用于在公式中表示对人而言具有特殊意义的事实, 事件, 状态等含义.

需要注意, 逻辑系统不具备解读和分辨符号的能力, 并且往往一个公式的意义或它的真伪性完全取决于我们如何解读该公式中包含的符号.

对应地, 若某个公式是真的, 则无论我们如何解读该公式中的符号, 都不会影响它的真伪性.

下面考虑一阶逻辑语义的形式化定义:

定义 1.2.1 (基, 受限变量, 自由变量和句子)

1. 若某个公式不含变量, 则称其为 基 (Ground).
2. 公式 $f$ 中任何不受任一种量词约束的变量均为 自由变量, 否则为 受限变量.
3. 不包含 任何自由变量 的公式成为 句子 (Sentence).

下面给出一些记法:

若公式 $\phi$ 中含自由变量 $X$ ,则可记为 $\phi[X]$; 若将 $X$ 替换为 $V$, 则可使用记号 $\phi[V]$.

我们下面考虑对公式的 解释 (Interpretation):

定义 1.2.2 (解释, Interpretation)

解释 使我们可以为任何句子赋予对应的 真值 (Truth Value):

形式上 解释 可被表示为下列的元组

\[\langle \mathcal{D}, \mathcal{I}\rangle\]

其中 $\mathcal{I}$ 为基于非空域 $\mathcal{D}$ 上的解释. 一般地, 在表述解释时我们都会略去其作用域 $\mathcal{D}$.

解释 $\mathcal{I}$ 本质上是一个映射. 它:

1. 将任何常数符号映射到 $\mathcal{D}$ 中的某个元素

2. 将任何元数为 $n$ 的函数符号映射到函数

   \[D^{n} \rightarrow D\]
3. 将任何谓词符号映射到某个真值

4. 将任何元数为 $n$ 的谓词符号映射到函数

   \[D^{n} \rightarrow \mathbb{B}\]

在对 不为常数 的 基 进行解释时, 我们可以递归地利用下列性质:

这一性质同样可以作用在 非谓词的原子 (Non-Propositional Atoms) 上:

需要注意上式中三个等号的含义均 各不相同:

左侧等号表示两个项 $t_1, t_2$ 在语法上相同, 中间的等号表示左右两侧的公式在定义上相同, 而右侧的第三个等号表示的含义是域元素的相等性 (注意 解释的本质 )

我们进一步考虑对 等价性 (Equality) 的解释:

随后考虑对公式 (Formula) 的解释:

然后给出对模型 (Model) 的解释:

需要注意, 在对公式中的变量重命名 (Rename) 时, 我们需要在重命名受限变量时注意 一致性. 在后文中, 我们一般假定所接触到的公式都是经过规范化 (Rectified) 的.

最后给出对 可满足性, 一致性和重言性 的定义:

定义1.2.3 (可满足性, 一致性, 重言性)

1. 若存在某个解释使某个公式在其解释下为真, 则称该解释是该公式的一个 模型.
2. 某个解释 满足 某个公式, 若它满足该公式的 全称封闭式 (Universal Closure, 用全称量词约束给定公式中全体自由变量所得到的封闭公式).
3. 称某个公式为 可满足的 (Satisfiable) 或 一致的 (Consistent), 若该公式至少有一个模型.
4. 称某个公式是 重言 的, 若它的任何解释都满足它.
5. 对应地, 若某个公式不存在任何模型, 则称其为 不可满足 (Unsatisfiable) 或 不一致 (Inconsistent) 的.

显然, 可以得出下列结论:

记 $\Gamma$ 为一系列公式的合取 (Cunjunction), $\phi$ 为一个句子 (Sentence), 则:

1. $\phi$ 的模型恰好是无法作为 $\neg \phi$ 的模型的那些解释.

2. 若 $\Gamma$ 是不一致的, 则必有 $\Gamma \vDash \text{false}$.

3. $\Gamma \vDash \text{false}$, 当且仅当 $\Gamma \cup {\neg \phi} \vDash \text{false}$.

4. 若 $\Gamma$ 不一致, 则它没有模型; 由于 $\text{false}$ 同样没有模型, 因此 $\Gamma$ 的任何模型都是 $\text{false}$ 的模型.

我们下一步将讨论对象推广到 表示为合取范式 的 一系列公式 上. 由此, 我们可以讨论 知识库的一致性. 进一步地, 为了检验某个公式在给定知识库的所有解释下的含义均为真, 我们需要引入 蕴含 的概念:

定义 1.2.4 (蕴含, Entailment)

称公式 $\phi$ 由一系列公式组成的集合 $\Gamma$ 所 蕴含, 若 $\Gamma$ 的任何模型都是 $\phi$ 的某个模型, 记为

\[\Gamma \vDash \phi\]

该性质同样可称为: “$\phi$ 是 $\Gamma$ 的一个结果 (Consequence)”.

我们以对 “处理查询” 的讨论结束本节. 问题 或 查询 可被视为 某个受存在量词约束的合取式 或某个 需要被实例化的, 包含自由变量的公式.

我们采用后者, 并在此基础上进一步假定 任何作为查询的, 含有自由变量公式 都是 被存在量词所闭合的, 如:

由此, 给定知识库 $\Gamma$ 和查询语句 $\exists X. \phi[X].$, 我们的目标是找到替换 $\sigma$, 使

为了达成这一目标, 我们需要将问题转换为

并引入一个全新的谓词 ans.

2. 联合与前向链式推理法

2.1 替换与联合

我们首先讨论 替换 的概念:

定义 2.1.1 (替换, Substitution)

替换 $\sigma$ 实质上是从将变量映射到项的有限函数 (Finite Function).

一般我们提到的替换均为 同步替换 (Simultaneous Replacement): 在基于替换规则对某个公式中的符号进行替换时, 对每一条规则的执行和匹配都是 同时进行 的, 如: 考虑规则

则有

而非

同时称:

$E\sigma$ 为 $E$ 的一个 实例 (Instance) 而 $E$ 是 $E\sigma$ 的一个 归纳 (Generalisation).

定义 2.1.2 (联合, Unification)

称两个项 $t_1, t_2$ 联合, 若存在某个替换/联合子 (Substitution/Unifier) $\sigma$, 使得

\[t_1 \sigma = t_2 \sigma.\]

进一步地, 我们称 $t_1$ 和 $t_2$ 是匹配的, 若

显然可知, 本质上 匹配是一种特殊的联合, 若某两个项是匹配的, 则它们 一定是联合的. 联合的目的是找到两个待联合项的 “最大公约实例” (Most general common instance). 注意上式中的等号所表示的是 语法上的等价, 联合不关心一阶逻辑所无法解读的语义.

在最好的情况下, 我们希望找到的联合子 (或称匹配的替换) 是 最一般的, 也就是说它所蕴含的信息是最为简练的, 删去任何一部分都会导致它不再能够作为两个项的联合子 (或匹配的替换).

对于任意的项 $s, t$, 我们记它们之间的 最一般的联合子 为

我们可以参考下列的例子:

我们下面考虑 Occurs Check. 它所描述的是对下列可能的情况进行的检查:

在执行联合时, 将被联合的变量同时出现在等式两端且结构不同 (如: 等式一端是变量, 而另一端是某个函数谓词).

在这一情形下我们需要执行 Occurs Check, 如果发现联合目标确实符合这一特征则需要终止尝试联合, 否则将会导致无限循环, 具体例子已在博文: Prolog 入门: 联合与证明搜索 中有所介绍, 不再赘述.

我们下面对 Robinson 联合算法进行简单介绍:

Robinson 联合算法可以视为一系列规则:

我们下面给出两个例子:

注意例子中每一步所使用的规则类型以及第二个例子中的最后一步. 在此处我们使用了 check 规则, 而该规则的实质就是执行 Occurs Check, $x \in \text{vars}(t)$ 的含义就是 “$x$ 在结构 $t$ 中”.

在实际问题中, 我们往往需要解决的问题更为简单, 一般表现为 “给定事实 $f_1, f_2$ 和某个替换 $\sigma$, 检查这两个事实在替换的作用下是否匹配”. 对于这样的问题, 我们可以使用表现为下列伪代码的算法解决:

1
2
3
4
5
6
7
8
9
10
def match(f_1 = name_1(args_1), f_2 = name_2(args_2), sigma):
    if different(name_1, name_2):
        return false
    for i in range (length(args_1)):
        if isVariable(args_1[i]) and args_1[i] != sigma:
            sigma = disjunction(sigma, {args_1[i] -> args_2[i]})
        elif (args_1[i])sigma != args_2[i]:
            return false
    
    return sigma

2.2 可决定性问题

我们首先回顾 可决定性问题 (Decidability) 的概念:

定义 2.2.1 (可决定性, Decidability)

我们称某个回答必为 “是” 或 “否” 的问题为 可决定性问题, 若存在某个以该问题的任何实例为输入并总能给出正确答复的算法.

在实践中, 类似搜索, 图染色, 求背包问题的最优解等问题均属于具备可决定性 (Decidable) 的问题, 而类似停机问题等则为不具备可决定性的问题.

由于我们可以将停机问题转化为完全等价的, 实质上是检查一阶逻辑的一致性问题, 因此由于前者是非可决定性问题, 后者也是同样不具备可决定性的. 因此, 我们无法解决检查一阶逻辑的一致性问题.

但是, 一些一阶逻辑的真子集–如谓词逻辑则为具备可决定性的 (即使它是 NP-Hard 的).

在一阶逻辑中, 具备可决定性的部分 (片段) 有:

1. 单元片段 (Monadic Fragment)

   在单元片段中, 任何谓词元数均不超过 $1$, 且不存在函数符号.

2. 双变量片段 (Two-variable Fragment)

   在双变量片段中, 任何公式最多由两个变量所构造.

3. 受保护片段 (Guarded Fragment)

   ???

4. 前束片段 (Prenex Fragments)

   若某个公式为前束范式且可被写为

   \[\exists * \forall * .F\]

   的形式, 则其属于前束片段.

2.3 Datalog片段

下面我们介绍这样的一个一阶逻辑的子集: Datalog.

需要注意的是, 在下面的内容中我们将不对非逻辑元素进行介绍, 若在概念定义上和真实的 Datalog (实质是 Prolog 语言的一个真子集) 存在差异的话, 一切以本课程提供的材料为准.

我们首先描述 Datalog 片段的语法:

在 Datalog 片段中, 公式均具备如下所述的形式:

其中称蕴含符号 $\implies$ 左侧的公式为 体 (Body), 右侧的为 首 (Head).

$p_{j}[X_j]$ 则为应用到 $X_j$ 中一系列常量或变量上的谓词符号, 使

且

即:

1. 所有变量均受全称谓词约束.
2. 首公式中任何涉及的变量均在体公式中使用过.

同时, 若某个公式的体是空的, 则称其为 事实 (这也很好理解, 无需基于任何前束条件就可推导出或者自然成立的陈述显然属于事实); 若不然, 则称其为 规则. 需要注意: 事实中不可包含任何变量!

我们随后解释 Datalog 中的一些术语和惯例:

1. 一般称 谓词 为 关系, 因谓词所描述的就是事物之间的关系.
2. 称一元谓词为 属性 (Property).
3. 在假定命名唯一时, 称常量为 对象 (Objects).
4. 对谓词, 函数, 常量的命名以小写字母开头.
5. 一般用大写字母指代变量.
6. 由于语法限制, 我们无法表示含有 $\neg, \vee, \exists$ 的公式或函数. 但在一些特殊情况下, 我们可以通过取这些公式的合取范式的方式绕过语法规则的限制.

下面考虑对 Datalog 知识库的解释.

首先需要注意的是, 任何 Datalog 知识库必须至少有一个解释.

同时, 我们假定 唯一命名假设 (Unique Names Assumption) 和 域闭包假设 (Domain Closure Assumption) 成立:

定义 2.2.2 (唯一命名假设和域闭包假设)

唯一命名假设: 知识库中任何名称不同的元素都是不同的.

域闭包假设: 域中的所有元素都被明确提及.

我们知道, 任何解释 $\mathcal{I}$ 都可用于表示全体在它的解读下表意为真的基式 (Ground Formula, 即不含变量的公式). 记由解释 $\mathcal{I}$ 所表示的这样的集合为 $\mathcal{I}$ 的闭包, 记为 $\vert \mathcal{I}\vert.$

同时记 $R$ 为由所有 Ground Rules 组成的集合, 这些 Ground Rules 是通过 grounding all rules by the constraints in the problem 得到的.

下面我们可以对唯一最小模型进行定义:

定义 2.2.3 (唯一最小模型, Unique Minimal Model)

我们称恰好满足下列性质的解释 $\mathcal{I}$ 为 唯一最小模型:

1. $\mathcal{I}$ 包含知识库中的全部事实.
2. 若 $\mathcal{I}$ 包含 $R$ 中任何一条规则的体 (Body),则它必须同时包含该规则的头 (Head).

上述的两条要求是对 “$\mathcal{I}$ 能够成为知识库的一个模型” 的最小要求, 恰好满足这些要求的模型是知识库的最小模型, 它是唯一的.

2.4 前向链式推理

推理的基础是知识库 (Knowledge Base) 和查询 (Query). 在执行推理时, 显然基于推理方向的不同我们有两种选择:

1. 从知识库开始, 通过执行 前向链式推理 检查我们的知识库能否满足查询.
2. 从查询开始, 通过执行 反向链式推理 检查我们的知识库是否支撑我们的查询.

而在本节中, 我们所考虑的是 前向链式推理. 在介绍它前, 首先需要引入一些基本知识:

定义 2.3.1 (结果和闭包, Consequence, Closure)

称知识库所蕴含的任何事实或任何在闭包中的事实均为知识库的 结果.

回忆前一小节, 在 Datalog 中, 闭包定义了它的唯一最小模型. 我们如下定义闭包:

定义 2.3.2 (闭包)

考虑知识库 $\mathcal{KB}$ 包含事实集合 $\mathcal{F_0}$ 和规则集合 $\mathcal{RU}$, 定义通过状态转换得到的下一状态下的事实集合如下:

\[F_i = F_{i-1} \cup \{(\text{head})\sigma \vert \text{body}\implies \text{head} \in \mathcal{RU}, \text(body)\sigma \in \mathcal{F_{i-1}}\}\]

在满足 $F_{j} = F_{j-1}$ 时, 状态转换无法再产生新的效果. 称此时到达 不动点 (Fixed Point), 此时的 $F_i$ 就是闭包.

下面我们需要关心的问题是:

1. 如何找到这样的匹配 $\sigma$?
2. 如何高效地计算 $F_{i+1}$?

我们首先考虑最简单的例子:

1
2
3
4
5
6
7
8
9
10
11
12
def match(body, F):
    matches = {∅}
    for f_1 in body:
        new = ∅
        for sigma_1 in matches:
            for f_2 in F:
                sigma_2 = match(f_1, f_2, sigma_1)
                if sigma_2 != ⊥:
                    new.add(sigma_2)
        matches = new
    return matches

上述的例子存在低效的问题, 同时检查 body 中元素的顺序也会明显影响算法运行的时间复杂度.

我们再讨论前向链式推理算法:

1
2
3
4
5
6
7
8
9
10
11
12
def forward(facts F_0, rules RU):
    F = ∅, new = F_0;
    do
        F = F ∪ new
        new = ∅
        for (body=>head) ∈ RU:
            for σ ∈ match(body, F):
                if (head)σ not in F:
                    new.add((head)σ)
    while new != σ
    return F

我们最后讨论查询.

在给定知识库后, 显然下一步我们希望执行的操作是对这个知识库进行 查询 (Queries). 查询语句可以是不含变量的 (Grounded), 也可以包含变量.

任何知识库 $\mathcal{KB}$ 对某个给定查询 $q$ 的回答均可表示为集合 $\text{ans}(q)$:

即: 所有在应用到查询 $q$ 时均能生成一个不含变量的事实, 且生成的事实是知识库 $\mathcal{KB}$ 中的一个结果的替换所组成的集合.

显然我们也可以将回答定义成知识库 $\mathcal{KB}$ 的闭包:

显然知:

1. 在查询 $q$ 不含任何变量时, 不存在任何替换满足条件, 因此在该情况下该查询的答复 $\text{ans}$ 为空集.
2. 在任何情况下, 答复 $\text{ans}$ 必为有限集.

随后, 我们解释如何使用前向链式推理生成这样的集合 (即: 生成查询的结果).

在此我们给出一个非常简单 (低效) 的, 可用于构造答复的算法:

3. 反向链式推理和语义归结

3.1 Prolog 片段

在本节中我们将对一阶逻辑的另一个片段 (或者称子集/部分) : Prolog 片段 进行介绍, 它同时也是我们将在本课程中使用的函数式程序设计语言: Prolog 的逻辑组成部分.

我们首先说明为何需要在已有 Datalog 片段的前提下还需要考虑名为 Prolog 的新片段. 我们产生定义新片段的主要需求是 Datalog 存在大量限制:

1. 显然, Datalog 不允许我们定义任何 需要 (或可以被) 无限解释的对象, 如常见的数据结构: 列表, 树和数字, 而数据结构在建模中是非常必要的.

2. 我们同时需要 函数 从而对存在量词所表示的含义进行建模.

   比如, 考虑陈述 “姚老师每一门课都考的很好”, 则要对它进行建模的话, 我们就需要一个能够从 “课程” 映射到 “结果: 考得很好” 的函数.

3. 此外, Datalog 缺乏对 等价/相等 的定义.
4. 最后, 我们无法使用 Datalog 对 否定 (Negation) 进行建模.

为了维持 Datalog 片段的优秀属性, 如可确定性, 同时补全它的定义所带来的诸多表意上的限制, 我们需要构造新的一阶逻辑片段, 而这就是我们将要介绍的 Prolog 片段.

我们首先介绍 Prolog 片段的语法. 和 Datalog 相比, Prolog 片段中, 公式 的结构大体相同“

但此时在公式结构中, 公式体中的任意 $p_i$ 可以为:

1. 包含 $X$ 中的项的谓词符号
2. 等式, 如 $x=y ~~\text{for}~ x, y \in X$
3. 不等式, 如 $x \neq y ~~\text{for}~ x, y \in X$

而公式头仍然只能为第一种.

不难看出, 这样的语法定义放松了对变量的限制, 且使用 项 扩展了 Datalog 片段. 然而到此为止, 基于上述语法定义的 Prolog 片段 是不支持否定谓词和析取谓词的, 它仍然是 Prolog 语言的一个子集.

随后我们考虑 Prolog 片段中的 唯一最小模型.

我们认为 Prolog 中所有 语法不同 的项均不相等, 而项之间的等价性是通过联合 (Unification) 达成的. 这和一阶逻辑不同: 在一阶逻辑中, 我们允许

这在 Prolog 中是完全不可能的.

在 Datalog 中, 我们需要在解释中令不同的常量和域变量一一对应, 而在 Prolog 中我们可能需要无限多个常量才能达成这一点.

形式上地, 对解释中常量的要求称为 有限项代数的一阶逻辑理论, 可被表示为下列的一阶逻辑:

1. 域闭包:

1. 差异性:

1. 单射:

1. 无环路 (无循环定义):

3.2 反向链式推理

我们下面讨论反向链式推理. 在正式开始对反向链式推理的讨论前, 我们首先举例说明为何在 Prolog 中反向链式推理是必要的. 考虑下面的例子:

1
2
even(zero)
X = succ(succ(Y)), even(Y) :- even(X)

显然上述知识库中定义的规则刻画了所有的偶数.

假设我们查询 even(succ(succ(0))), 由于根据 succ() 谓词的推理规则可知 succ(succ(0)) 为偶数, 因此在该例子中无需计算出域闭包也可解决这一问题.

随后假设查询 even(succ(0)). 由于此时我们除了计算整个域闭包之外没有其他方法归结出 “succ(0) 不是偶数” 的结果, 而这个问题由于扩展到所有偶数上因此域闭包是无限大的, 因此产生了矛盾: 前向搜索无法遍历无限大的域闭包, 由此搜索过程永无法停止, 进而我们无法生成对这一查询的答复.

基于上述的例子可知, 即使我们可以在 Prolog 中使用前向链式推理解决部分问题, 在 知识库闭包无穷大 的前提下, 我们 永无法通过前向链式推理达到不动点. 因此, 我们需要引入反向链式推理来应对知识库闭包无穷大的情况.

定义 3.2.1 (反向链式推理, Backward Chaining)

反向链式推理的核心思想是从目标出发, 通过将联合的目标 拆解成多个子目标 并分别解决它们从而解决问题.

考虑同一个例子. 使用反向链式推理尝试给出 even(succ(succ(0))) 的解答时:

1. 首先检查查询语句本身是否已经是知识库中的某个事实.
2. 若不是的话, 检查它是否与知识库中的任何规则的首 (Head) 联合.

由于 even(succ(succ(0))) 可以和知识库中唯一一条规则的首 even(X) 联合, 其联合结果为

由此, 我们就将问题简化为: 尝试联合陈述

而由于对上述的陈述联合的结果恰为知识库中的唯一一条事实 even(0), 因此上面的陈述成立. 由此我们可知, 我们的知识库满足用户的查询.

再考虑第二个查询 even(succ(0)). 将它和唯一一条规则的首联合得到的结果是

由此得到的新联合目标是

由于

无法联合, 因此可知该查询的答复是 fail.

若我们的知识库更加复杂, 包含多条可供在尝试联合查询时作为备选的规则, 则我们在联合失败某条规则但又没有穷尽对规则的选择时就需要 回溯 到导致联合失败的前一个 选择点 处做出新的选择, 这一流程和 Prolog 的证明搜索规则是一致的.

3.3 反向链式推理算法和搜索树

本节中我们将对反向链式推理算法进行介绍并使用数个简单的例子进行说明.

我们首先给出完整的反向链式推理算法:

or_query 实质上所执行的是将查询 $q$ 和知识库中每条规则都尝试联合了一遍 (Disjunction), 只要有一个规则能够和查询联合即说明知识库能够支撑这个查询.

而 and_query 接受一个存储不同查询语句的列表 queryList L 作为参数之一, 并检查列表中的全部查询是否都能够与知识库中的事实和规则所联合.

我们进一步解释 or_query() 和 and_query() 方法:

3.4 归结

在上面的几节中, 我们已经介绍了前向链式推理和反向链式推理的基本概念和实现, 分别介绍了 Datalog 片段和 Prolog 片段这两个一阶逻辑的子集. 下面我们从逻辑的角度总结我们所介绍的内容.

在执行链式推理时, 我们从目标 $G$ 出发并尝试将其与闭包 $\mathcal{F}$ 匹配. 这一过程可视为

其中

上式含义是: $\neg G$ 和 $\mathcal{F}$ 均为不可满足的, 因此闭包 $\mathcal{F}$ 蕴含 $G$.

在反向链式推理中, 我们从一系列子目标

出发, 并在 满足了所有目标后, 即我们得到 $\perp$ 时, 终止推理. 因此, 我们可以将反向推理的目标列表视为

下面我们引入 归结 以解决 “如何基于更一般的蕴含条件进行推理” 的问题.

定义 3.4.1 (归结原则, Resolution)

对任意子句 $l_1, \cdots, l_i$, $m_1, \cdots, m_j$, 若某一对子句 $l_p$, $m_q$ 恰为 互补的 (Complementary), 则下列逻辑归纳原则成立:

\[\frac{(l_1 \vee \cdots \vee l_i) \vee (m_1 \vee \cdots \vee m_j)}{(l_1\vee\cdots\vee l_{p-1}\vee l_{p+1}\vee\cdots\vee l_{i}) \vee (m_1\vee\cdots\vee m_{q-1}\vee m_{q+1}\vee\cdots\vee m_{j})}.\]

而称对互补的这一对子句 $l_p, m_q$ 归结. (resolve on $l_p$ and $m_q$).

举例而言:

下面说明归结原则的 正确性 (Soundness):

定义 3.4.2 (推理规则的正确性)

称任意给定的推理规则是 正确的, 若它的结论对于任何其前件条件的模型而言都是真的.

对于上面的例子而言, 我们有以下结论:

下面介绍 子句 和 文字 的概念:

定义 3.4.3 (子句和文字)

称 文字 为原子或原子的取反, 子句 为一系列文字的析取.

子句中可能包含一定量的原子以及其他原子的取反形式. 因此, 可以将子句视为:

\[(A_1 \wedge \cdots \wedge A_m) \rightarrow (B_1 \vee \cdots \vee B_n)\]

注意:

1. 除非特别说明, 否则认为子句都是 隐含地全称量化 (Implicitly Universally Quantified) 的.
2. 空子句是 假的 (False).
3. 含肯定形式的文字数量最多为 $1$ (即 $n \leqslant 1$) 的子句称为 Horn 子句.
4. 恰含一个肯定形式的文字的子句是 明确的 (Definite), 对知识库的定义应用了这样的子句.

从下面开始, 我们不加说明地规定: 记$t, s$ 为项, $I$ 为文字, $C, D$ 为子句.

归结原则同样适用于子句:

考虑下面的例子:

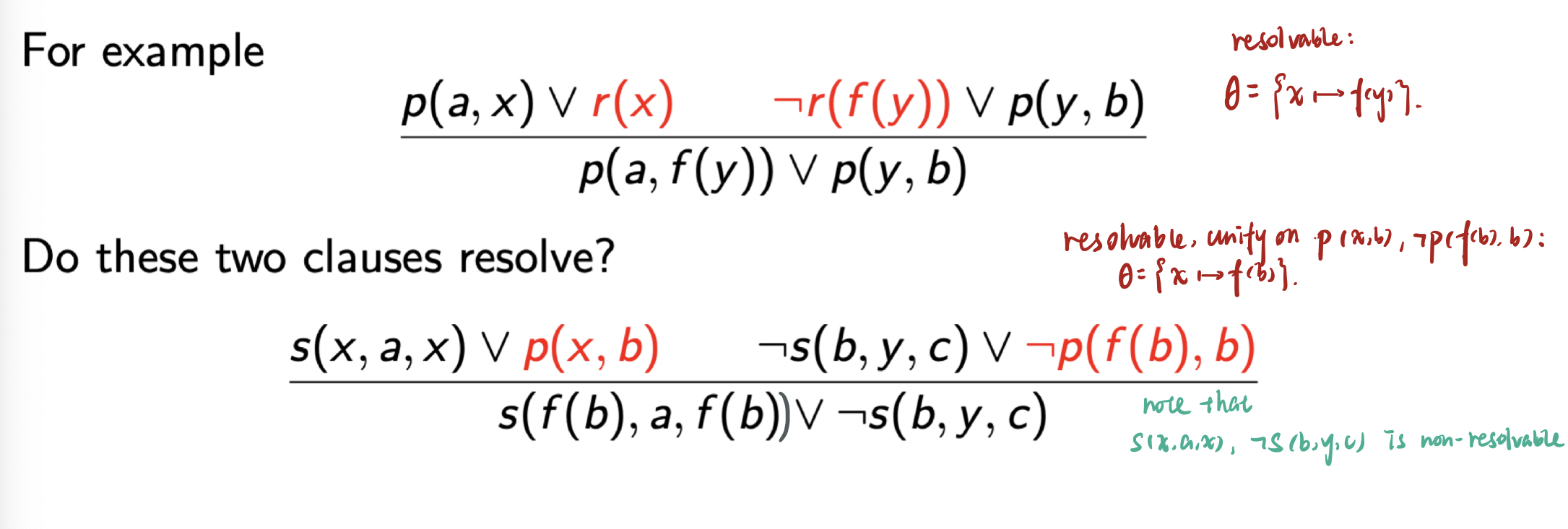
需要注意: 在联合来自两个不同的子句中的文字时, 需要 首先对变量命名以避免冲突:

同时, 通过对变量命名, 我们还可以实现 “自归结”:

我们接下来介绍在反向链式推理中应用的, 一种特殊的归结原则: SLD-Resolution.

回顾 Prolog 术语, 结合此前引入的 子句 的概念, 可以看出:

在只需要考虑 Horn 子句的情况下, 我们可以通过引入一种特殊的归结原则, 从而提高推理的效率.

此时, 我们有:

1. 知识库中的事实和规则形如

   \[H \vee \neg B_1 \neg \vee \cdots \vee \neg B_n\]

2. 目标或查询形如

   \[\neg(G_1 \wedge \cdots \wedge G_m) = \neg G_1 \vee \cdots \vee \neg G_m\]

因此我们只需考虑 目标子句和某个事实/规则子句 之间的归结, 从而生成形如下面所示的子目标子句:

显然, 要执行归结, 我们需要在一系列 Horn 子句中寻找一对自相矛盾的, 从而满足 SLD-Resolution 的条件.

需要注意, SLD-Resolution 的执行时间复杂度是线性的, 这意味着每个目标子句都只需要被考虑一次.

SLD-Resolution 具备完备性, 这意味着如果某个问题有解, 我们一定可以使用这一方法找到它.

在一些特定情况下, 在使用反向链式推理法生成某个查询的答复时, 由于反向链式推理可能无法终止, 它有可能会漏掉一些本可被找到的解答, 这是因为反向链式推理法 不是公平的:

定义 3.4.4 (公平)

若某个搜索策略不会无限期地延迟推理, 则称其为 公平 的, 如广度优先搜索.

我们最后讨论一种向基于反向链式推理的 Prolog 片段中引入 取反 同时不要求我们必须放弃 SLD-Resolution 而使用更低效的 Full Resolution 的方法: 否定即失败 Negation as Failure.

一般在对问题建模时, 我们希望引入 对一些情境的否定 的定义, 如:

也就是

而由于这个陈述的的两种形式都 不是明确的子句, Prolog 知识库中的任何一条规则或事实都必须是明确的子句, 因此基于定义无法对它应用反向链式推理和 SLD-Resolution.

但在特殊情况下, 我们可以归纳出一些事实的否定:

考虑某个 基事实 (Ground Fact, 不含变量) $f$ 并且我们无法通过反向链式推理证明它成立, 则我们可以断定它的否定, 即 $\neg f$.

这一情形能够成立的原因是, 对 Prolog 知识库 $\Gamma$ 和任意基事实 $f$, 要么

要么

换言之, 任何解释要么是 $f$ 的模型, 要么是 $\neg f$ 的模型, 并且这一结论对于 $\Gamma$ 的模型恒成立.

这意味着若我们在反向链式推理中以某个基式 $A$ 为条件, 而若无法通过反向链式推理证明 $A$ 被知识库满足, 则可知知识库蕴含 $\neg A$, 称这样的情形即为 否定即失败: 对 $A$ 联合的失败蕴含了 $\neg A$.

REFERENCE:

First-Order Logic 1 Syntax of First-Order Logic

人工智能 一种现代方法 第8章 一阶逻辑 - CSDN

命题逻辑和一阶逻辑

Occurs check - Wikipedia

• Previous
  计算机视觉导论：图像合成
• Next
  计算机图形学导论：矩阵, 向量和着色器