数据库导论 大二上期末总复习

数据库导论 关系数据库理论

DROP 'theory' FROM 'dbKnowledgeBase';

Posted by R1NG on January 11, 2022 Viewed Times

COMP23111 REVISION Ch1

本复习笔记对本学期所教授的课程内容进行了基于笔者自己理解下的重排.

笔者将前八周内对关系数据库从建模到通过网络编程实现, 穿插部分数据库理论的松散体系拆分为三个部分: 数据库理论, 数据库建模和数据库实现, 而最后三周内对各种非关系数据库的介绍仅作为补充内容 , 放在 “其他数据库” 中.

1. 数据库理论

数据库是 一系列有价值的信息组成的结构化的集合 (A structured collection of meaningful data).

我们称任何有价值的信息为 数据, (Data) 用于构建和维护数据库的软件为 数据库管理系统 (DBMS, Database Management System), 而 数据库管理系统 和 数据 共同组成 数据库系统 (Database System).

我们还称 标准化的, 用于 管理关系数据库 和 操作关系数据库数据 的计算机语言为 SQL, 而不完全遵循关系模型的数据库 (如以 MongoDB, Couchbase, Redis 为例的文件型数据库, 以 Neo4j 为例的图数据库).

称 CREATE, ALTER, DROP, RENAME 等建表相关的語句為 数据定义语言 DDL, 也就是 Data Definition Language; INSERT, UPDATE, DELETE 等直接对 数据 进行操作的语句为 数据操作语言 (DML, Database Manipulation Language), 以 SELECT 语句为例的, 用于执行信息查询的语句为 数据库查询语言 (DQL, Data Query Language). SQL 是由上述三种语句组合而成的.

1.1 概念和逻辑模型

在本课程中, 我们着重介绍的数据库类型是 关系数据库. 因此, 我们需要先将需求提炼为一种称为 实体-关系模型 的概念模型 (Conceptual Schema), 并将概念模型具体实现为关系数据库.

定义 1.1.1 (概念模式)

概念模式 (Conceptual Schema / Conceptual Schema) 是对用户数据需求的 精确描述, 包括 实体类型 (Entity Type), 实体之间关系的类型 (Relation Type) 和 对关系的约束 (Constraints). 用户数据需求使用不涉及具体实现细节的概念表示, 本质上是对现实的抽象和简化, 便于理解.

数据库设计人员可使用概念模式作为和甲方的交流手段, 并可通过检查所构造的概念模式确保甲方的所有数据需求是否得到满足.

定义 1.1.2 (逻辑模式)

逻辑模式 (Logic Schema / Logic Schema) 是指可被商用 DBMS 直接运行的数据库实现.

将概念模式这种 抽象化的高级数据模型 转换为逻辑模式这种 具体的实现化数据模型 的步骤称为 逻辑设计 (Logical Design), 该步骤得到的结果就是数据库的 逻辑模式.

我们下面简介本课程中介绍的唯一一种概念模型: 实体-关系模型.

1.2 实体-关系 (E-R) 模型

定义 1.2.1 (E-R 模型)

实体-关系模型 (Entitiy-Relationship Model) 是通过从现实世界中抽象出 实体类型, 实体的属性 和 实体间的关系, 从而对现实世界建模的概念模式.

定义 1.2.2 (实体)

实体 是 E-R 模型所表示的最基本对象, 它是现实世界中 独立存在的事物, 可以是物理存在, 也可以是概念存在.

定义 1.2.3 (实体类型)

实体类型 定义为一个 具有相同属性的实体组成的集合. 每个实体都具有一种 类型, 某个实体类型可以具有多个实例.

定义 1.2.4 (码)

码 (Key) 定义为 在实体-关系模型中可用于唯一确定 (Uniquely Identify) 某个实体的属性, 也就是说每个不同实体的这个属性值都不相同.

对任何实体类型而言, 其中的每个实体实例都必须能通过某个码唯一确定. 对实体类型而言, 码 可以不唯一.

若某个实体类型 本身既没有可作为码的属性, 又没有被赋予的码 (Assigned Key), 则称该类型为 弱类型 (Weak).

需要注意: E-R 模型中 码 的概念和关系数据库中的 主键/外键 定义有 明显区别, 不可混淆, 但是可以适当地将 码 和 备选键 (Candidate Key) 类比.

定义 1.2.5 (属性)

属性 是用来描述 实体 的某些 具体性质 的数据. 对特定的实体而言, 其每个属性都具有特定的值.

E-R 模型通常使用的属性类型有: 简单/复合属性, 单值/多值属性, 存储/派生属性:

定义 1.2.6 (简单/复合属性)

称 不可被继续划分的属性 为 简单属性 或 原子属性, 复合属性 由组成它的简单属性的值组合而成.

定义 1.2.7 (单值属性/多值属性)

称 某个特定实体 的 只具有一个值 的属性为 单值属性, 而该实体的 具有多个值的属性 为 多值属性, 如 某个人 的 学位 (这个人可以没有学位, 也可以拿了双学位).

定义 1.2.8 (存储属性/派生属性)

在某些情况下多个属性的值是相关的, 如我们可以从某人的生日计算出此人的年龄.

称如 “年龄” 这样的, 可以由某个其他属性计算得出的属性为 派生属性, 而称 “生日” 这样作为派生依据的属性为 存储属性.

在某些情况下, 某些属性值还可由 相关实体 派生得到.

定义 1.2.9 (空值)

空值 NULL 在 对某个实体而言没有适用的值 或 该实体的这个属性值缺失 时应用, 其语义依具体情况差异而有不同.

定义 1.2.10 (复杂属性)

由复合属性和多值属性嵌套得到的组合称为 复杂属性.

定义 1.2.11 (关系)

关系 描述 不同实体类型 之间的联系, 将两个或更多实体类型使用某种含义 (Meaning) 相连接, 如考虑实体: Axton 和 COMP23111, 在 “Axton 通过了 COMP23111” 中, 通过 就是一个 二元关系.

注: E-R 模型中的关系受 基数约束 (Cardinality Constraint), 它由所被建模的关系而决定 (回顾一下一对多, 一对一, 多对一等基数约束类型). 我们将在数据库建模一节中详细描述如何在 E-R 表 (Entity-Relationship Diagram) 中表示实体类型之间的关系所受的基数约束.

1.3 数据库的关系模型

数据库的三种基本模型是 层次模型, 网状模型, 关系模型, 其中以 数据库的关系模型 应用最为广泛.

定义 1.3.1 (数据库的关系模型)

关系模型 将数据库表示为 由关系组成的集合.

若我们将每个关系视为一个 表格 (Table)时, 每个表都表示一个相关数据集的集合 (某个实体集), 每一行表示一个实体, 其内容的实质是抽象而来的 事实, 一般对应现实世界中的某个实体或者某个联系.

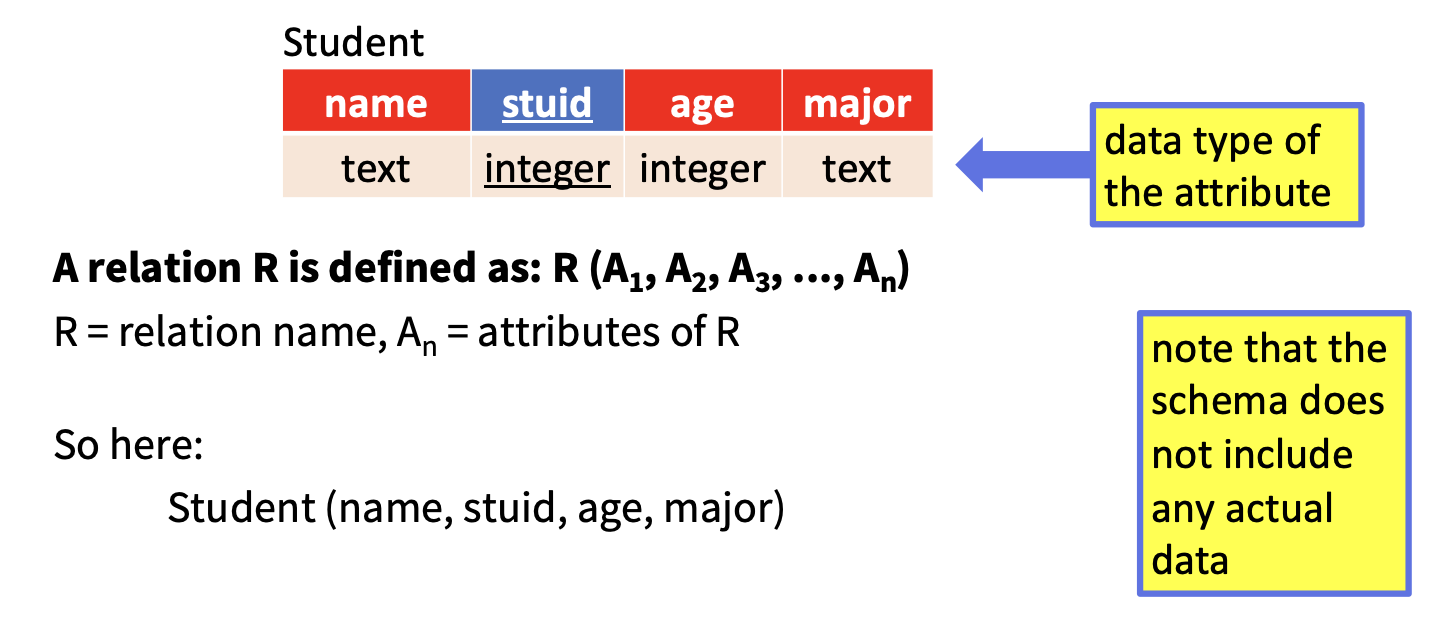
20220113113232

如上图所示, 对某个关系而言, 其表名和列名分别用来解释每一行/列的值所代表的含义.

需要注意, 关系模型本身只是对某种关系的建模, 并不包含实际的数据本身.

在正式的关系模型术语中, 行称为 元组 (Tuple), 列标题称为 属性 (Attribute), 表称为 关系, 数据类型称为 域 (Domain):

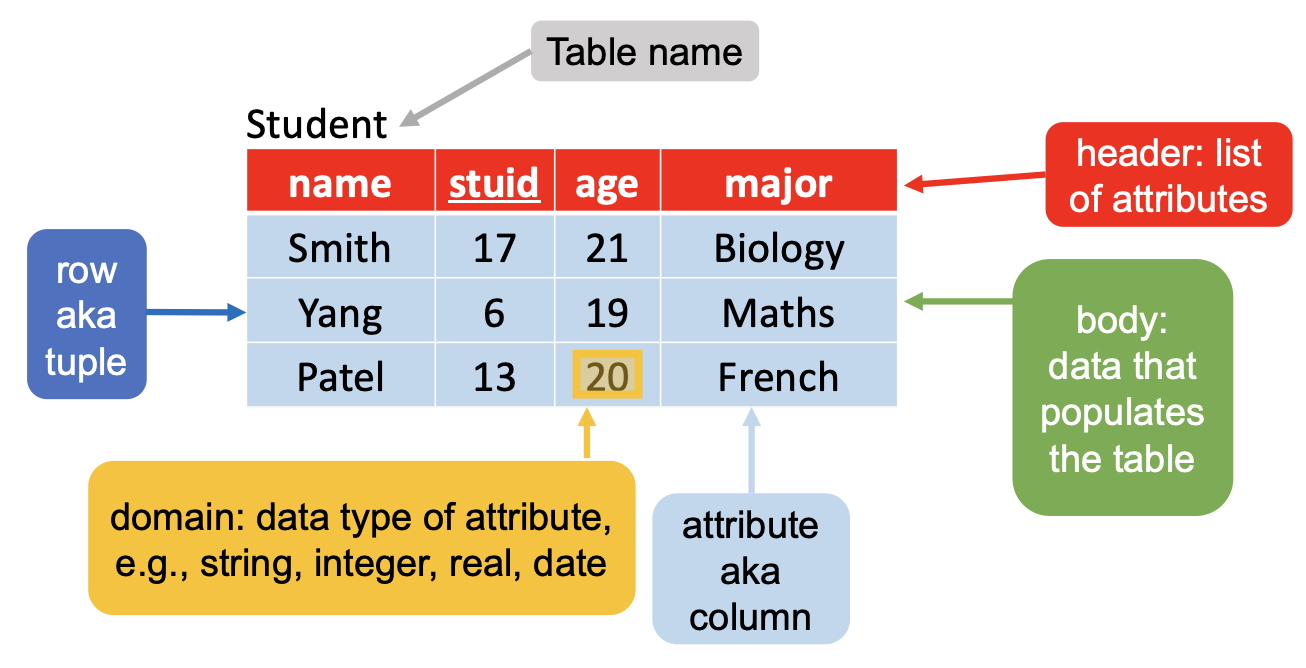
20220113114155

下面我们对这些术语进行定义:

定义 1.3.2 (域)

称 域 是 不可再分的原子值 组成的集合.

一般而言, 指定一个域的通常方法是 指定某个数据类型 , 从而确保 构成这个域的数据值都来自这个数据类型.

在本课程中, 我们可以近似地认为域就是数据类型.

定义 1.3.3 (关系模式, Relational Schema)

关系模式 $R$ 表示为

\[R(A_1, A_2, \cdots, A_n),\]

由关系名 $R$ 和属性列表 $A_1, A_2, \cdots, A_n$ 共同构成. 每个属性 $A_i$ 都是一个变量名, 它可取的值在某个域 $D := \text{dom}(A_i)$ 中.

关系的 度/元 (Degree 或 Arity) 是该关系模式中 属性的个数 $n$.

在上面的例子中, 我们描述了一个名为 Student, 度为 $4$ 的关系, 在 E-R 模型中, Student 被解释为 实体类型. 在关系模型中, 原先的 “实体类型” 被解释为 “关系”, 也就是说实体的本质被视为是将某种和一系列不同 属性 聚合的关系, 而原先实体类型之间的关系被用主键和外键表示.

定义 1.3.4 (键/超键)

称在某个关系表中的, 能够用于唯一标识元组 (也就是实体集中的某个特定实体)的属性集 为 键.

定义 1.3.5 (主键)

称在候选键组成的集合中被 选定 用来唯一标识某个元组的键为 主键 (Primary Key).

定义 1.3.6 (超键, Super Key)

称 能唯一标识元组 的属性集为 超键.

定义 1.3.7 (候选键, Candidate Key)

称 能唯一标示元组 且 不含多余属性 的属性集 为 候选键.

注: Gareth把 超键 和 候选键 的定义搞反了. 正常的候选键就是如 定义 3.7 这样定义的.

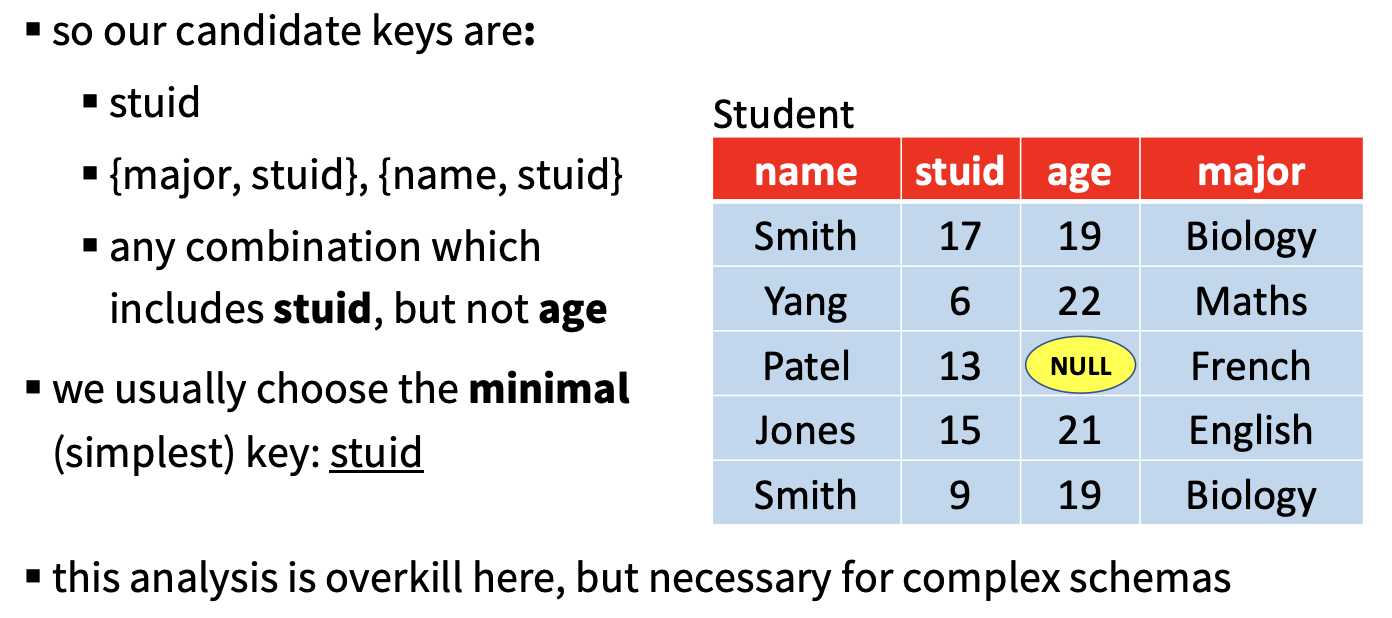
20220113125232

由于Stewart在讨论函数依赖和范式时仍然沿用了正常的候选键和超键的定义, 本人姑且认为Gareth的Slide里出现的Candidate Key定义是错的, 一切以 Wikipedia 和其他经典数据库教材为准.

参考 这里 和 这里

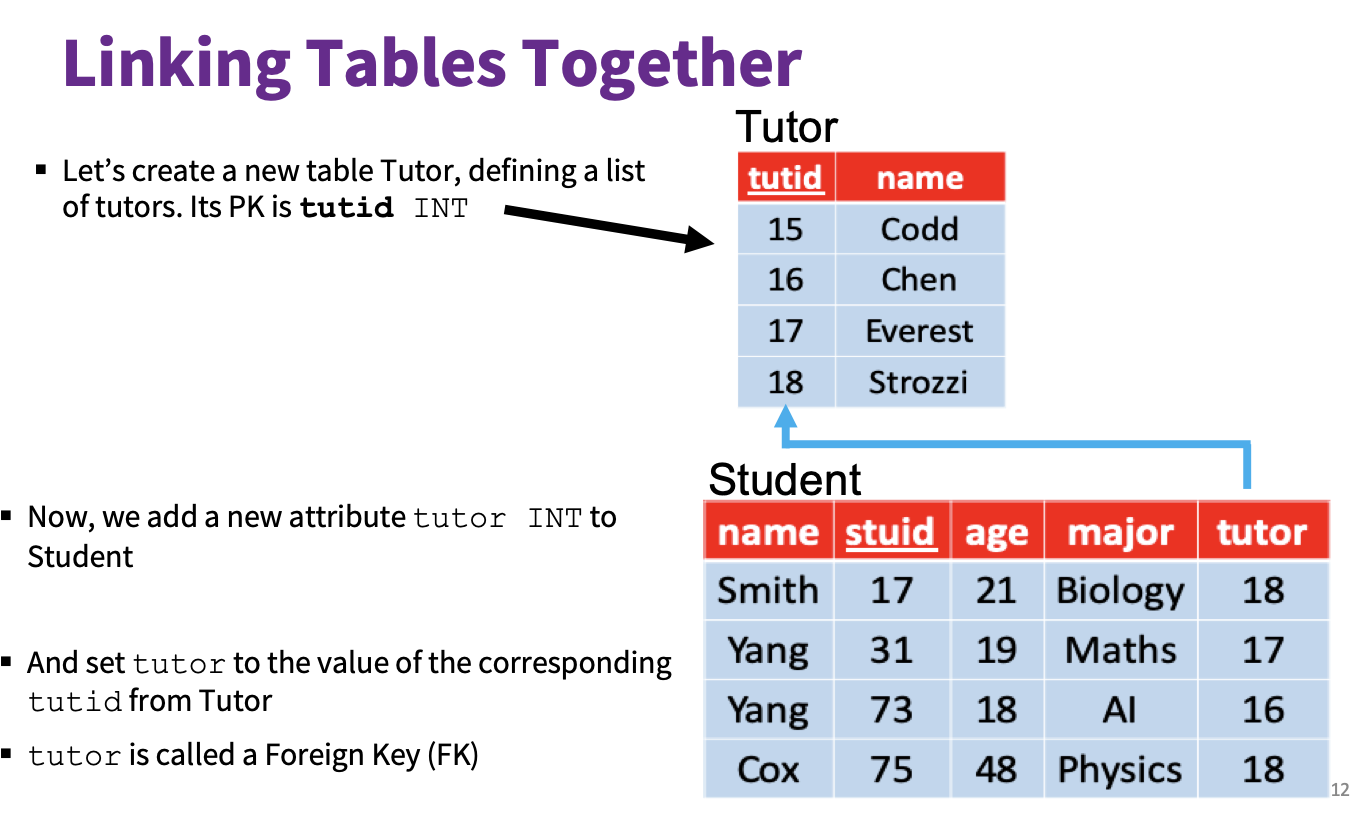
定义 1.3.8 (外键)

称某个元组中, 出现在其他元组里且作为其他元组的主键的属性为 外键. 外键具备连接元组与元组的职能.

20220113125750

定义 1.3.9 (数据库模式)

数据库模式 (Database Schema) 定义了数据库中各表的结构和他们之间的关系, 本质上是对关系模式 (Relational Schema) 的提炼: 它只包含对各个关系所定义的规则, 而不包含实际的数据.

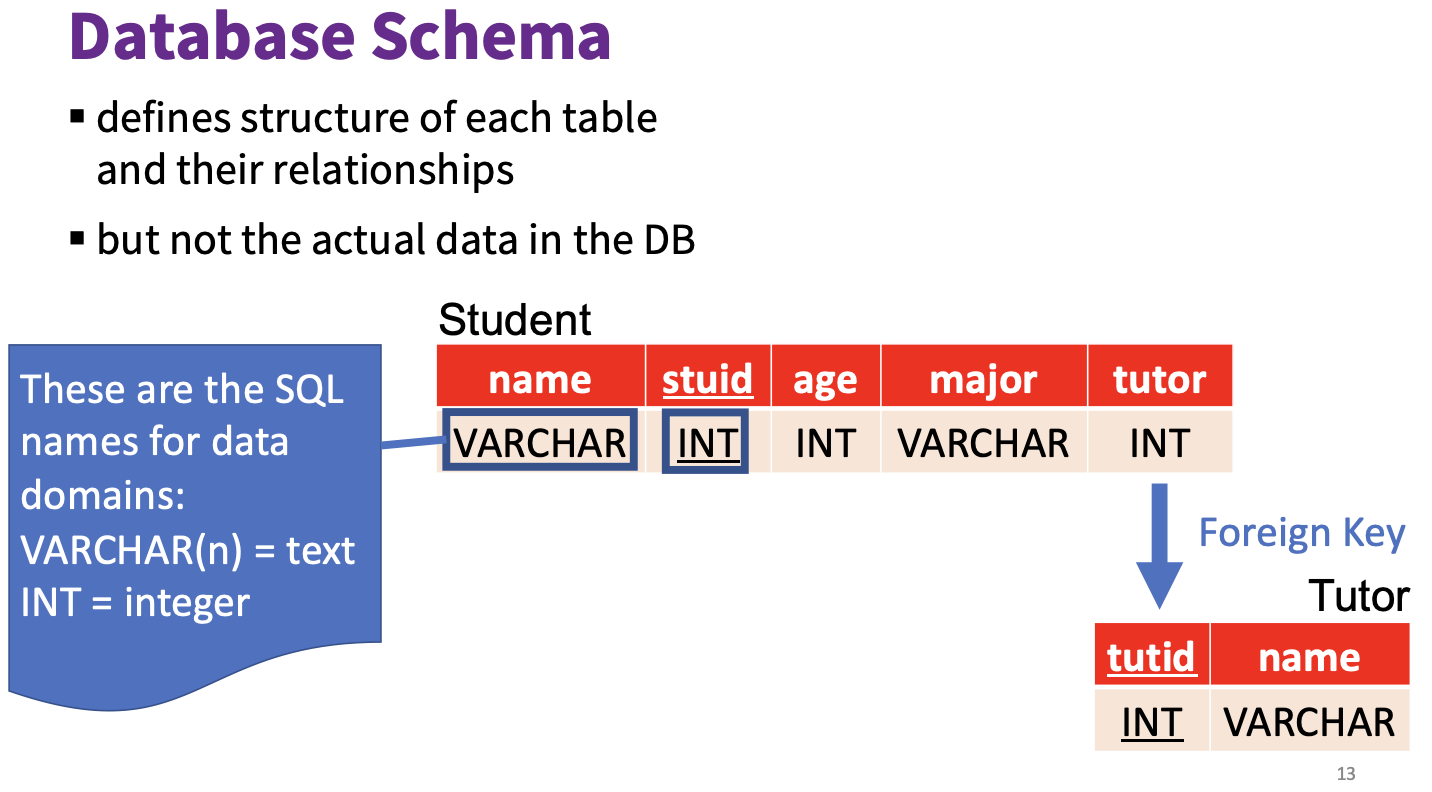
20220113130917

下面讨论关系模型中的数据完整性约束:

关系模式中涉及的操作包括 CRUD: 插入 (Create), 查找 (Retrieval),修改 (Update), 删除 (Delete). 而数据库在执行这些操作前都会检查操作是否满足数据库的 完整性约束 (Integrity Constraint), 从而防止用户在修改数据库时不会破坏 数据库的一致性. 完整性约束包含下面的几种类型:

  1. 主键约束 (Primay Key Constraint): 确保数据字段的 唯一性 和 非空性.

  2. 唯一约束 (Unique Constraint): 确保数据字段的 唯一性. (但是可为空)

  3. 检查约束 (Check Constraint): 限制该数据字段的范围和格式.

  4. 默认约束 (Default Constraint) 赋予该数据字段规定好的默认值.

  5. 外键约束 (Foreign Key Constraint): 需要建立两表间的关系并引用主表的列.

最后简单总结:

20220113130605

1.4 函数依赖 (Functional Dependencies) 和范式 (Normal Form)

我们先讨论 函数依赖, 它是关系模式设计理论中的重要概念:

定义 1.4.1 (函数依赖)

若在某张表中, 在 属性集 $X$ 的值确定的情况下, 必能 唯一确定 属性 $Y$ 的值, 则称 属性 $Y$ 是 函数依赖于 属性 $X$ 的, 记为

\[X \rightarrow Y.\]

或称属性 $X$ 函数决定了 属性 $Y$.

20220113171957

定义 1.4.2 (完全函数依赖)

若某张表满足函数依赖关系 $X \rightarrow Y$, 则若对于属性组 $X$ 的任何一个 真子集 $X’$, 满足

\[X' \nrightarrow Y\]

则称 $Y$ 对于 $X$ 完全函数依赖, 记作

\[X \overset{F}{\rightarrow} Y.\]

定义 1.4.3 (部分函数依赖)

和 完全函数依赖 相对地, 若属性 $Y$ 是 函数依赖于 属性 $X$, 但并不 完全函数依赖于 它, 则称 $Y$ 部分函数依赖于 $X$, 记为

\[X \overset{P}{\rightarrow} Y.\]

定义 1.4.4 (传递函数依赖)

若:

  1. $Y$ 函数依赖于 $X$;
  2. $Z$ 函数依赖于 $Y$,

则称 $Z$ 传递函数依赖于 $X$, 记为

\[X \overset{T}{\rightarrow} Z.\]

定义 1.4.5 (主属性)

称 包含在任意一个候选键 (属性集) 中的属性 为 主属性.

定义 1.4.6 (非主属性)

称 不包含在任意候选键中的属性 为 非主属性.

我们可以通过一系列推理规则, 从已知的一些函数依赖推导出另外一些函数依赖, 而这些规则就被称为 Armstrong 公理:

20220113173309

其推论:

20220113173334

20220113173346

20220113173357

在此基础上, 对任何由一系列函数依赖规则组成的集合 $U$ , 对于该集合中的任意一个真子集 $F$ 而言, 我们都可以 使用上面提到的规则 计算出 基于全体规则 $U$, 从 $F$ 出发可被逻辑推导出的全部函数依赖规则. 在解决一些题目时, 可以用这种方式快速确定超键.如:

20220113174051

我们下面给出不同级别范式的定义与它们的转换原则:

为了确保我们设计得到的关系模式 (Relational Schema) 具备最小的数据冗余且存在最少的 CRUD 异常, 需要通过对给定的关系模式进行一系列的检验, 以 “验证” 我们的关系模式是否符合某些特定的标准, 也就是所谓的 “范式”.

随后, 我们可以基于不同范式的相应标准对我们的关系模式进行验证和评估, 并根据实际需要对我们的关系模式中不满足标准的某些关系进行进一步分解, 从而将其规范化.

定义 1.4.7 范式

范式 是 符合某种级别的关系模式的集合, 表示了某个关系内部各个属性之间的联系的合理化程度, 换做人话来说就是 关系模式的表结构所符合的设计标准的级别.

而 关系的范式 则是该关系所能满足的最高的范式条件, 表现了这个关系规范化的程度.

在本课程中, 我们关心的范式分为 第一范式 (1NF) , 第二范式 (2NF) 和 第三范式 (3NF).

定义 1.4.8 (第一范式)

第一范式基于 原子化 的概念: 它规定属性域只能包含不可再分的 (原子化的) 值, 且元组中任一属性的值必须是一个来自于该属性域的, 单个的值.

换言之, 1NF 不允许 “关系中嵌套关系” 或 “元组中任何一个属性值是关系”.

比如, 考虑下图所示的关系模式 Department, 假设属性 Dlocations 值不唯一, 则该关系模式不满足 1NF:

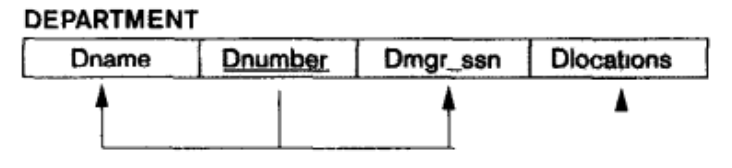
20220113175935

在本课程中, 我们介绍了下述的, 将这样的关系模式转换为 1NF 的方式:

从这个关系模式中移除导致违背 1NF 要求的属性 (在我们的例子中是 Dlocations), 并将它和原模式 DEPARTMENT 的主码 Dnumber 放在单独的一个新关系中, 这个新关系的主码依据实际情况决定, 在本例中则为 {Dnumber, Dlocations}. 这一方法的实质是: 将某个非 1NF 的关系分解为多个 1NF 关系.

定义 1.4.9 (第二范式)

第二范式基于 完全函数依赖 的概念:

若关系模式 $R$ 中的每个非主属性 $A$ 都 完全依赖于 $R$ 的主键, 则该关系模式属于 2NF.

换言之, 如果给定的关系模式的主键的任何一个真子集能够唯一确定某个不在主键内的属性, 则这个关系模式就不是 2NF.

如果主键只由单个属性组成, 则无需进行 2NF 检验, 这个关系模式一定是 2NF.

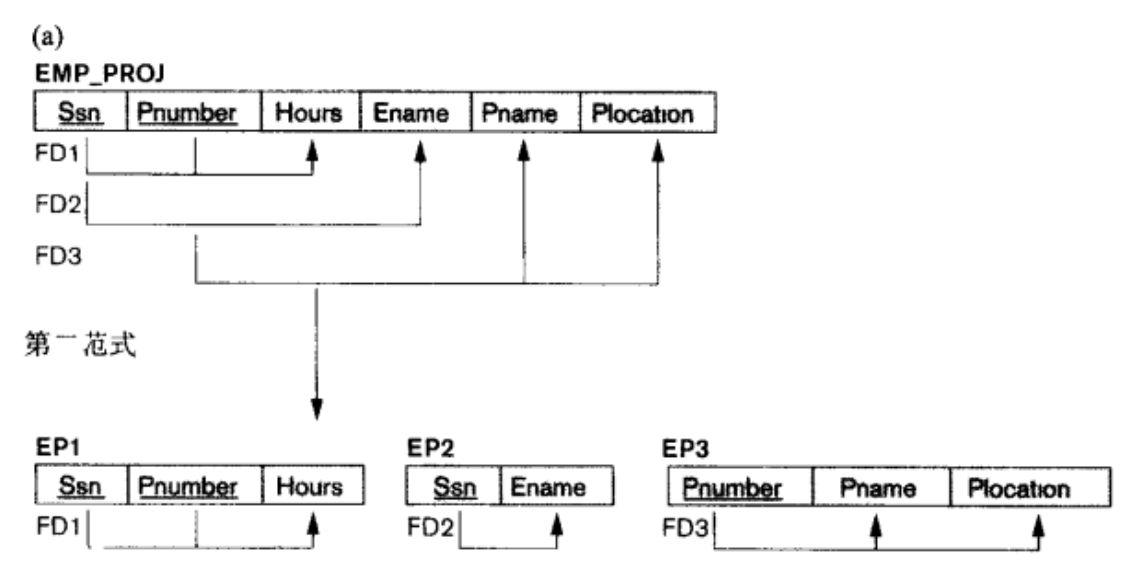
本课程中所介绍的, 将 1NF 转化为 2NF 的流程是: (注意: 不要跨级转化范式!)

考虑某个不属于 2NF 的关系模式, 我们需要:

  1. 找到那些部分依赖主键的属性.

  2. 确定它们分别 完全依赖于主键的哪个组成部分.

  3. 将原来的关系进行拆分, 每个部分依赖主键的属性都要被从原关系中拆分出来, 和它所完全依赖的那一部分主键组合在一起形成一个满足 2NF 的, 更小的关系.

20220113182028

定义 1.4.10 (第三范式)

第三范式基于 传递依赖 的概念: 若某个关系模式 $R$ 满足 2NF 范式, 且 $R$ 中不存在 非主属性传递依赖于主码 的情况, 则 $R$ 属于 3NF.

换言之, 关系模式中所有的非主属性都应该直接依赖于主键. 若存在某两个非主属性 $Y, Z$, 对于主键 $X$, 有

  1. $X \rightarrow Y$
  2. $Y \rightarrow Z$

则这个关系模式就不是 3NF.

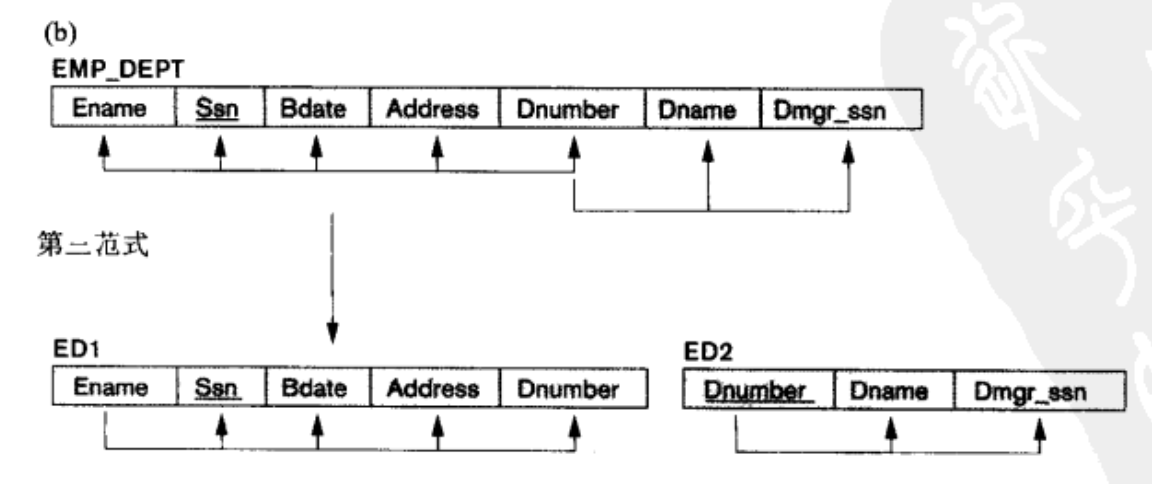
本课程中介绍了下述的 3NF 转换方法:

  1. 找到间接依赖主键的属性链条.

  2. 拆分关系, 打散链条.对于间接依赖链条上除了主键以外的每个节点, 都要单独分解为 3NF 模式进行规范化.

20220113182914

综上所述, 我们可以将基于主码的范式和相应的规范化的检验条件和规范化方法总结如下:

20220113183006



REFERENCE

Entity Relationship Diagram (ERD) Tutorial - Part 1

Entity Relationship Diagram (ERD) Tutorial - Part 2

Wikipedia: Conceptual schema

CATALOG
    FEATURED TAGS
    COMP12111 课程笔记 前端学习 50P50D 大二上期末总复习 大二下期末总复习 大一上期末总复习 大三上期末总复习 人工智能 数据结构与算法 大一下期末总复习 逻辑学 高级计算机图形学 COMP15111 扩展自习 COMP21111 奇技淫巧 机器学习 计算机图形学 COMP11212 Prolog 人工智障 自然语言处理 大三下期末总复习 数据库导论 COMP15212 博弈论 数据结构和算法 数值计算方法 算法 软件工程概论 Lab
    FRIENDS