自然语言处理

本章将研究如何利用以自然语言描述的知识, 并介绍对自然语言进行信息检索和信息提取的一般方法.

1. 语言模型

形如 Java, Haskell 的程序设计语言都有 精确定义的语言模型, 这种语言可以被定义为 字符串的集合, 并且可以 通过一组称为 “语法” 的规则描述. 形式语言也可通过规则来定义 程序的意义或语义.

而自然语言, 如 English 或 中文, 则无法被描述为一个 确定的语句集合, 因此我们一般需要通过 句子的概率分布 而非 集合 定义自然语言模型.

换言之, 给定某个字符串 “Axton is so strong!!!111”, 我们关注的是一个随机的句子恰为这个字符串的概率是多少, 而非考虑这个字符串是否属于定义语言的句子集合.

同时, 自然语言具有歧义: 一个句子在不同的语境下可以解释为多个含义. 我们往往难以只用一个意义来解释某个句子, 而需要使用多个意义上的概率分布.

最后, 需要说明的是, 自然语言的规模极其庞大, 并且时刻处于变化和演化之中. 因此, 我们的语言模型只能是 对自然语言的模拟.

2. $n$ 元字符模型

本质上说, 自然语言的 文本 是由 字符 组成的, 如英语中的 字母, 数字, 标点, 空格 等. 因此, 最简单的语言模型就是 字符序列的概率分布.

记 从 $c_1$ 到 $c_N$ 共 $N$ 个字符构成一个文本序列 的概率为

\[P(c_{1 : N}).\]

定义 2.1 ($n$ 元组)

称 长度为 $n$ 的书写符号序列 为 $n$ 元组 (n-gram) 的.

注意, 我们分别用 unigram, bigram 和 trigram 表示 一元组, 二元组 和 三元组.

定义 2.2 ($n$ 元模型)

称 $n$ 个字符序列上的概率分布 为 $n$ 元模型.其中, 构成自负序列的元素不仅可以是字符, 也可以是 单词, 音节 或其他单元.

定义 2.3 (Markov 链)

我们可以简单地认为某一时刻状态的确定 只依赖于在此之前的 $n$ 个状态 的状态链为 $n$ 阶 Markov 链.

$n$ 元模型 (不只局限于 $n$ 元字符模型) 可以定义为 $n-1$ 阶 Markov 链. 显然, 在一个 三元模型 (也就是 $2$ 阶 Markov 链) 中, 我们有:

\[P(c_i \vert c_{1 : i-1}) = P(c_i \vert c_{i-2: i-1}).\]

也就是说在三元模型中任何位置上的字符 $c_i$ 为某个字符的概率只由于它前面的两个位置上的字符决定.

在三元模型中, 我们结合 链式规则 和 Markov 假设 定义长为 $N$ 的字符序列的概率:

\[P(c_{1:N}) = \prod_{i=1}^{N}P(c_i \vert c_{1:i-1}) = \prod_{i=1}^{N}P(c_i \vert c_{i-2:i-1}).\]

对于某个包含 $n$ 个字符的语言的三元字符模型, $P(c_i \vert c_{i-2:i-1})$ 有 $n^3$ 项参数. 我们可以通过对包含大量字符的文本集合进行精确的计数统计而得到, 我们称文本的集合为 语料库 (Corpus).

我们可以使用字符模型完成 文本题材分类, 拼写纠错, 语言识别 等任务.

3. $n$ 元模型的平滑

$n$ 元模型的问题在于 训练语料只提供了真实概率分布的估计值, 而无法提供所有的边界情况. 因此, 我们需要采取措施使我们的语言模型能够有效地 扩展到在语料库中从未见到过的文本上.

要实现这一点, 我们要通过改进语言模型使在训练文本库中出现概率为 $0$ 的字符序列仍能够被赋予一个 很小的非零概率值, 并将其他的数值同样小幅度下降使得概率的完备性仍然成立, 这一过程也被称为 平滑:

定义 3.1 (平滑)

称通过赋予给定训练数据集中出现频率极低或未出现的数据一个较小的频率值, 从而使频率模型能够被扩展到一般情形的, 调整低频计数的过程为 平滑.

我们下面给出两种常用的简单平滑方法:

1. Laplace 平滑:

   Laplace 平滑指定, 若某个随机布尔变量 $X$ 在目前已有的 $n$ 个观察值中恒为 false, 则

   \[P(X = \text{true}) = \frac{1}{n+2}.\]

   换言之, Laplace 平滑假定 多进行两次试验, 可能 一个值为 true, 另一个为 false.

2. 回退模型和线性插值平滑

   回退模型的基本思想是: 首先进行 $n$ 元计数统计, 若某些序列的统计值 很低或者为零, 则回退到 $n-1$ 元.

   线性插值平滑是一种通过线性插值将 三元, 二元和一元模型 组合起来的后退模型. 线性平滑插值定义概率估计值如下:

   \[\hat{P}(c_i ~\vert~ c_{i-2 : i-1}) = \lambda_{3} \cdot P(c_i ~\vert~ c_{i-2 : i-1}) + \lambda_{2} \cdot P(c_i ~\vert~ c_{i-1}) + \lambda_{1} \cdot P(c_i).\]

   此处系数满足

   \[\lambda_{3} + \lambda_{2} + \lambda_{1} = 1.\]

   参数值可以是固定的, 也可以通过某些算法进行计算. 关于参数值计算的讨论超出本文讨论的范围, 在此按下不表.

   在 $i=1$ 时, 表达式

   \[P(c_i ~\vert~ c_{i-2 : i-1})\]

   就退化为

   \[P(c_1 ~\vert~ c_{-1 : 0}),\]

   而在 $c_1$ 前并没有字符. 因此, 我们需要引入 人工字符 解决这一问题:

   我们可以定义 $c_0$ 为空字符, 也可以回退到 低价 Markov 模型, 定义 $c_{-1 : 0}$ 为 空序列, 从而

   \[P(c_1 ~\vert~ c_{-1:0}) = P(c_1).\]

$n$ 元字符模型可以被进一步扩展为 $n$ 元单词模型, 它检验的最小元素从 字符 变为了 单词. $n$ 元单词模型的平滑方法如下:

引入人工单词:

人为定义训练数据集中 每个首次出现的, 与之前遇到的所有单词都不同的单词 为 人工单词, 指定在训练数据集中未出现的单词具有的概率为 人工单词在训练数据集中出现的频率.

注意被定义为人工单词的单词不会发生改变, 如果 $a$ 在训练数据集中总共出现了 $x$ 次, 则它的第一个出现 $t$ 被指定为人工单词 $o$ 并不会使得它在训练数据集中出现的次数 $-1$, 它的出现频率 $n$ 和不将其第一个出现指定为人工单词时的频率相同.

4. 文本分类 (Text Classification)

我们下面讨论 文本分类 (Text Classification) 问题, 其本质是 给定一段文本, 判断它属于预定义的一系列类别中的哪一类, 其实例包括 情感分析 和 垃圾邮件检测.

归类的基本方法有两种: 语言模型方法 和 机器学习方法.

以垃圾邮件检测为例. 我们可以对垃圾邮件进行训练从而得到一个计算

\[P(\text{Message} ~\vert~ \text{spam})\]

的 $n$ 元语言模型, 并对正常邮件进行同样的训练, 得到计算

\[P(\text{Message} ~\vert~ \text{ham})\]

的模型. 随后, 我们可以应用 贝叶斯规则 对接收到的新消息进行分类:

\[\text{argmax}_{c \in \{\text{spam , ham}\}} P(c ~\vert~ \text{Message}) = \text{argmax}_{c \in \{\text{spam , ham}\}} P(\text{Message} ~\vert~ c) \cdot P(c).\]

注意此处 $P(c)$ 代表 垃圾邮件或正常邮件在训练数据集中的频率, 可以通过 统计垃圾邮件和正常邮件的数目 得到.

我们还可以使用机器学习方法: 将邮件信息视为一组 特征-值 对, 使用分类算法 $a$ 和特征向量 $X$ 进行判断.

我们可以将 $t$ 元组作为特征: 比如 $t=1$ 时, 我们考虑一元模型, 此时 在词汇表中的单词 就是 特征, 而特征的 值 就是每个单词在这条邮件信息中出现的次数.

我们称这样的 一元表示形式 为 词袋模型 (Bag of words): 它就如同把训练语料的单词放进一个袋子中, 每次从袋子里抽取一个单词从而构成邮件信息, 而需要注意的是, 该过程 不保留词语之间的相互顺序, 因此有 信息丢失.

在二元, 三元甚至更高元的模型中, 特征的数量成指数级别增长. 此外, 我们还可以加入邮件的一些 metadata 作为非 $n$ 元特征.

在选定了特征集后, 我们就可以使用常见的监督学习技术训练文本分类模型.

5. 信息检索 (Information Retrieval)

信息检索的本质是 检索和用户提供的信息需求相关的信息, 任何与信息搜索相关的工具都是信息检索系统的一个实例.

一个标准的 信息检索系统 ( IRS, Information Retrieval System) 都应具有下列四个特征:

1. 文档集合:

   每个 IRS 都应确定它需要处理的文档的类型和范围, 如 “一页文本”, “一个段落文本” 还是 “多页文本”.

2. 一个使用某种 查询语言 构造和描述的 查询请求:

   查询请求 明确地描述了用户的需求. 组成它的查询语言可以由单词列表, 由多个单词组成的句子, 布尔运算符和非布尔运算符组成.

3. 结果集合:

   IRS 应该能够基于特定的查询请求给出对应的查询结果, 它是 文档集合的子集, 包含了与查询请求相关的文档.

4. 结果集合的展示:

   IRS 同时应具备向用户展示其检索结果的能力.

检索模型

早期的 IRS 使用 布尔关键字模型:

文档集合中的每个词都被视为一个布尔特征: 若这个词出现在某篇文档中, 则该文档的这个特征值为真, 反之为假, 而查询语言就是 基于这些特征的布尔表达式语言: 只有当表达式的解释为真时, 文档才与查询相关.

布尔关键字模型的优点在于原理简单, 容易解释和实现, 而其最明显的缺点在于无法基于文章的贴合度生成相关性排序, 并且给出适当的表达式需要极高的知识门槛.

大部分 IRS 选择了 基于单词计数统计 的模型: 我们将在本节中介绍 BM25评分函数.

评分函数根据给定的某篇文档和查询语句, 基于内建规则执行计算并返回一个 数值 作为对这篇文档在给定查询语句下的相关度评分.

在 BM25 中, 得分是 由构成查询的每个单词的得分 进行 线性加权 组合而成. 查询项的权重受三个因素的影响:

1. 查询项在文档中出现的频率 TF:

   TF 表示 词项频率, 如对于查询 [Long live Axton], 频繁提到 Axton 的文档得分较高.

   注意 词项频率 (Term Frequency, TF) 的定义是: 给定的某个单词 在 给定的某篇文章 中 出现的频率:

   \[\text{TF}(t, d) = \frac{\text{raw count of term `t' in document `d'}}{\text{document `d's word count}}.\]

   但是在你校的课程中, 词项频率应该被定义为给定的某个单词在某篇文章中出现的次数!

2. 词项的文档频率的倒数 IDF:

   如假设单词 long 几乎出现在每个文档中, 则这个词项的 文档频率较高, 进而知其 IDF 较低, 因此 long 没有查询中的 axton 重要.

   注意 文档频率 (Document Frequency, DF) 的定义是: 在 全体文章 中 包含给定单词的文档 的 篇数. 它和 TF 是截然不同的两个东西:

   \[\text{DF}(t, D) = \frac{\text{total number of documents `D' which contains term `t'}}{\text{total number of documents in corpus `D'}}.\]

   但是在你校的课程中, 文档频率应该被定义为给定的某个单词在全体文章中出现的次数!

   同时注意 IDF 并不单纯是 DF 的倒数:

   \[\text{IDF} = \log_{10}\frac{N - DF + 0.5}{\text{DF + 0.5}}\]

   注意 IDF 中的平滑 ($+0.5$) 和为了控制数值范围而进行的取对数操作.

3. 文档的长度:

   文档的长度越长, 其包含单词的数量越大, 越可能提到所有查询中的单词, 但同时也越可能 携带更多与查询项无关的内容. 因此, 这类文档不一定真正与查询相关. 如果两篇文章都提到了查询中所有的查询项 (查询单词), 则更短的那篇应该作为更佳的相关文档候选.

我们将要讨论的 BM25 函数将上述的三个因素全部考虑在内:

不妨假设:

1. 语料库中的 $N$ 个文档都已经 索引完毕 , 因此对某个单词 $q_i$, 它在文档 $d_j$ 中的 词项频率 $\text{TF}(q_i, d_j)$ 可以被直接从索引中被查找到.

2. 已经构建好了一个 文档频率统计表, 因此对某个单词 $q_i$, 我们可以通过查表得到它在 整个语料库 中的 文档频率 $\text{DF}(q_i)$.

因此, 给定文档 $d_j$ 和由 词语 $q_{1:N} := q_1q_2\cdots q_{N}$ 组成的查询, 就有:

\[\text{BM25} (d_j, q_{1:n}) = \sum_{i=1}^{n} \text{IDF}(q_i) \cdot \frac{\text{TF}(q_i, d_j) \cdot (k+1)}{\text{TF}(q_i, d_j) + k \cdot (1-b + b \cdot \frac{\vert d_j \vert}{L})}.\]

我们下面对 BM25 计算公式中的变量进行解释:

1. $\vert d_j \vert$ 表示 文档 $d_j$ 以 单词计数 的长度 (包含了多少个单词).

2. $L$ 为 语料库中文档 的 平均长度:

\[L= \frac{\sum_{k=1}^{N} \vert d_k \vert}{N}.\]

1. $k$ 和 $b$ 均为需要结合具体语料库通过交叉验证进行调整的参数. 若未特殊指定, 认为 $k=2, b=0.75$!

对语料库中的每个文档都计算 BM25 评分往往是不现实的. 在给定某个查询时, 我们一般 对查询中的各个查询单词从索引中找出它们的命中列表并取交集, 再对这个交集里的文档依次计算评分.

对检索模型的评价

在评价某个 IRS 性能时我们有两个可供参考的度量指标: 召回率 (Recall) 和 准确率 (Precision).

假设对某个 IRS 进行一次用来检验其性能的查询, 系统返回了一个结果集合. 对查询结果结合语料库进行统计, 可以分别得到四个值:

1. 在结果集合中 的, 和查询 相关 的文档数.
2. 在结果集合中 的, 和查询 不相关 的文档数.
3. 不在结果集合中 的, 和查询 相关 的文档数.
4. 不在结果集合中 的, 和查询 不相关 的文档数.

准确率 所度量的是 结果集合 中 实际相关 的文档所占的比例.

误判率 所度量的是 结果集合 中 不相关 的文档所占的比例, 数值上和 1-准确率 相等.

召回率 所度量的是 结果集合 中 相关文档在整个语料库中 的 所有相关文档 中所占的比例.

漏报率 所度量的是 结果集合 中 实际相关 的文档在 所有相关文档 中所占的比例, 数值上和 1-漏报率 相等.

$F_1$ 值 是 综合准确率和召回率 这两个指标的度量: 它是 准确率和召回率两者 的 几何平均值:

\[\text{F}_{1} = \frac{2 \cdot \text{Precision} \cdot \text{RecallRate}}{\text{Precision} + \text{RecallRate}}\]

PageRank 算法

页面 $p$ 的 PageRank 定义为:

\[\text{PR}(p) = \frac{1-d}{N} + d \cdot \sum_{i}\frac{\text{PR}(\text{in}_i)}{C(\text{in}_i)}.\]

其中, $\text{PR}(p)$ 为 页面 $p$ 的网页排名, $N$ 为 语料库中总的网页数量, $\text{in}_i$ 为 链接到 $p$ 的页面, 而 $C(\text{in}_i)$ 为 从页面 $\text{in}_i$ 链接出去的网页链接数, $d$ 为一个称为 阻尼因子的常量, 可以理解为用户点击页面上任意一个链接的概率.

显然, PageRank 是 递归定义 的. 我们可以通过迭代计算出网页排名: 开始时, 所有页面的 PageRank 值均设为 $1$, 然后迭代运行算法, 更新排名, 直到收敛.

6. 信息提取 (Information Extraction)

定义 6.1 (信息提取)

称 信息提取 为通过 浏览文本 获取 特定类别的对象 和 对象间的关系 的过程.

信息提取的典型实例包括: 网络爬虫从网页中抽取实例信息, 从天气预报中抽取所报道的天气信息等数据库字段的内容.

在一些特定的领域内, 信息提取可以达到很高的准确率, 而在一般的领域内, 就需要 复杂的语言模型 和 复杂的学习技术.

基于有限状态自动机的信息提取

基于属性的抽取系统 (Attribute-based Extraction) 是最简单的信息提取系统, 它假设 整个文本都是关于单一对象 的, 而系统的任务是 从文本中抽取该对象的属性.

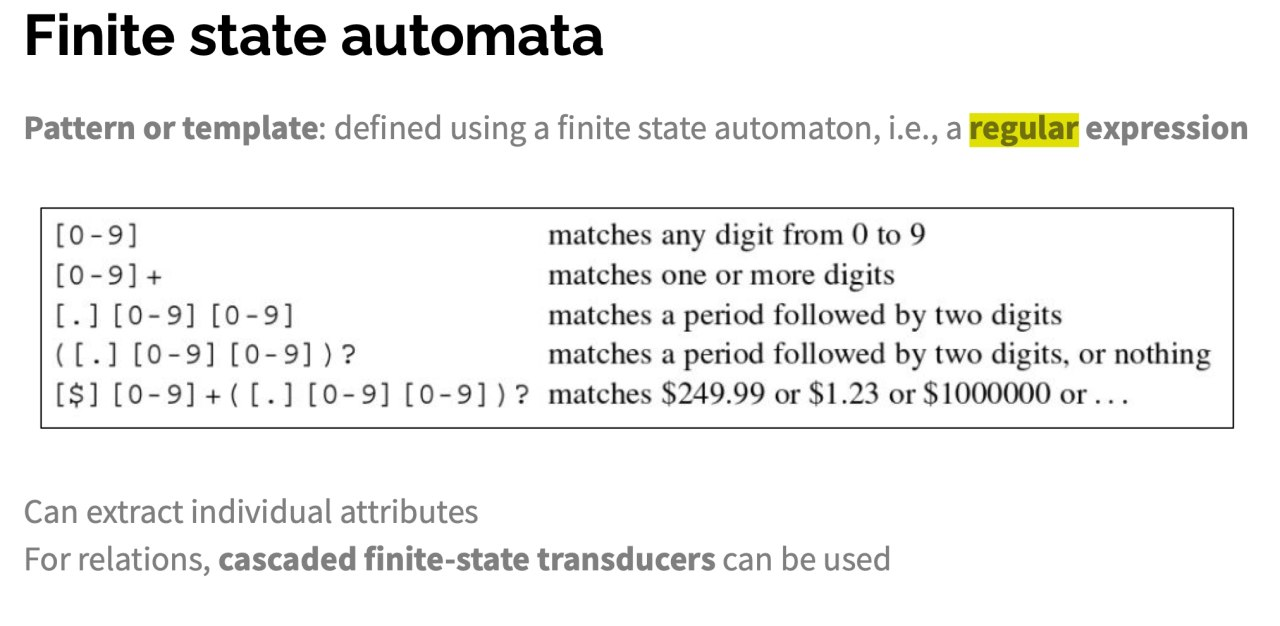
对于这类问题, 我们可以针对 每个需要抽取的属性 基于 有限状态自动机 定义模版. 模版的一个最典型的例子就是 正则表达式.

一般而言, 模版由 前缀正则表达式, 目标正则表达式 和 后缀正则表达式 组成. 这样的设计思想是: 某些属性的特征信息来源于属性值本身, 或者来源于属性值的上下文.

一旦某条属性的正则表达式和文本完全匹配, 就可以从文本中 抽取出表示属性值那部分的文本. 若没有匹配, 就需要 给出默认值 或让该属性 留空, 若有多个匹配则需要从中挑选.

课上介绍的正则表达式语法规则如下:

信息提取的概率模型

概率模型适用于从 有噪音的, 变化的文本 中抽取信息, 在这里我们使用 隐 Markov 模型.

隐 Markov 模型 (HMM) 描述了一个 隐含状态序列, 该序列的每一步都附有一个 观察值 $e_t$. 在这里, 为了将 HMM 应用于信息提取问题上, 我们 为每个属性分别建立一个独立的 HMM.

在这里, 观察值序列就是 文本的单词序列, 隐含状态分别表示 处于属性模版 的 目标, 前缀或后缀部分 或 (不在属性模版中的)背景部分.

例如, 下图给出了一个简短的文本和一个 HMM. 这个模型的功能是识别这条通知信息中提到的报告人:

其中, PRE 表示模版的前缀 (Prefix) 部分, T 表示模版的目标 (Target) 部分, 而 POST 表示模版的后缀 (Postfix) 部分, - 表示不属于模版中的背景状态.

在信息提取问题中, 使用 HMM 相比使用 FSA 有两大主要优势:

1. HMM 是 概率模型, 因此具有抗噪声的特点, 而在正则表达式中, 只要被检测的句子中哪怕有一个预期的字符丢失了, 正则表达式的匹配也会失败. 而若使用 HMM, 我们就可以很好地对句子中丢失的字符或单词进行 退化处理 (Degradation): 用概率值表示匹配的程度, 而非一刀切地用布尔值表示 “匹配成功” 或 “匹配失败”.

2. HMM 可以通过数据训练得到, 而无需构造复杂的匹配模版. 因此, 这样构造的模型还具有可扩展性的特点, 可以适应 随着时间推移不断变化 的文本.

需要注意的是, 在 HMM 中, 我们已经假定了这样的结构: 我们的 HMM 模版由一系列目标状态组成, 且 任何前缀状态 必须 在目标状态之前, 而 后缀状态 必须 在目标状态之后, 其他状态都表示 背景.

使用 HMM 进行信息提取存在一个问题: HMM 实际上是一个 生成模型, 除了进行信息提取之外, 它还可以依照同样的规则进行信息生成. 虽然 HMM 功能强大, 但它对很多和问题不相关的概率进行了建模, 而这些是我们不关心的. 自然地, 我们会考虑, 是否 不对这些不相关的概率进行建模得到的抽取模型性能会更好?

我们为理解文本所需的是 判别模型, 它可以为给定的观察值 (在这里就是文本) 建立 隐含属性的条件概率模型: 给定文本 $e_{1 : N}$, 条件模型将寻找使概率

\[P(X_{1:N} ~\vert~ e_{1:N})\]

最大化的隐含状态序列 $X_{1:N}$.

在前文提到的 会议报告 的例子中, 文本 $e_{1 : N}$ 就是第一行中给定的, 要被抽取信息的原文, 而得到的序列 $X_{1:N}$ 就是第二行中的模版匹配序列, 这个序列告诉我们在原文中的哪个单词最有可能是模版中的 目标, 前缀 或 后缀, 进而我们就可以以此为基准进行信息提取.

这类模型的一个重要架构是 条件随机场 (Conditional Random Field, CRF). 对于给定的观察变量集合, 条件随机场对 一组目标变量 的 条件概率分布 建模.

和 Bayes 网络 类似, 条件随机场也可以表示变量之间的依赖结构. 比如, 线性链条件随机场 (Linear-chain Conditional Random Field) 就可以表示 时间序列中变量之间的 Markov 依赖关系.

条件随机场模型的任务是: 给定观察序列 $x$, 返回标记序列 $y$, 且 $y$ 满足:

\[y = \text{argmax}_{y} ~ p_{\lambda}(y ~\vert~ x).\]

而

\[p_{\lambda}(y ~\vert~ x) = \frac{1}{Z_x} \cdot \exp(\sum_{i=1}^{n} \sum_{j=1}^{m} \lambda_j \cdot f_j(y_{i-1}, y_i, x, i))\]

其中:

1. $\frac{1}{Z_x}$ 是确保对所有的 $y$ 而言概率和为 $1$ 的 标准化因子.

2. \[\sum_{j=1}^{m} \lambda_j \cdot f_j(y_{i-1}, y_i, x, i)\]

   为 特征函数, 显见它被定义为 $m$ 个特征函数 $f_1, \cdots, f_m$ 的加权和. 其中, 参数 $\lambda_j$ 通过最大后验估计过程学习得到.

3. 指数幂上的 $\sum_{i=1}^{n}$ 作用为对标记序列 $y$ 中的每个标记 $y_i$ 求和 (也就是说特征函数要应用在每个标记上).

此外, 特征函数是 CRF 的重要组成部分: 它通过 相邻的状态, 全部的观察值序列 $x$ 和时序中的当前位置 $i$ 进行计算. 举例而言, 我们可以定义这样的一个特征函数:

---

• Previous
  人工智能导论 模糊逻辑
• Next
  人工智能导论 用于通讯的自然语言

---