模糊逻辑
我们使用 模糊逻辑 (Fuzzy Logic) 描述具有模糊性的语言形式和思维. 在应用中, 我们通过 模糊控制系统 (Fuzzy Control System) 使 Agent 得以基于 模糊规则 利用具有模糊性的现实事实并以此为基准作出可靠的决策.
标准的 模糊控制系统 架构如下图所示. 在接下来的数节中我们将详细介绍它:
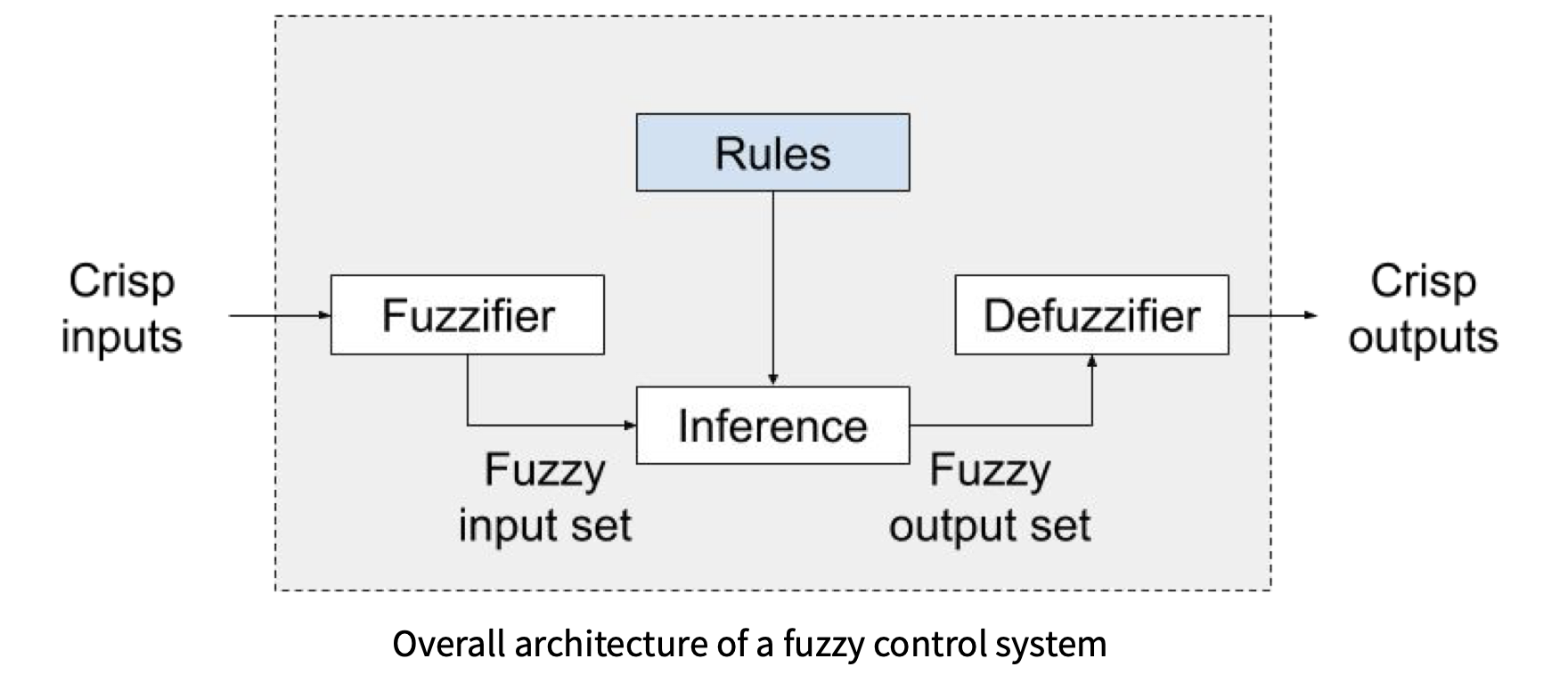
1. 隶属度 (Degree of Membership)
和此前介绍的传统逻辑 (或清晰逻辑) 不同, 在模糊逻辑中事物不是 非黑即白 的, 不能直接用 True 或 False 表达, 而需要取一个 介于 $0$ 和 $1$ 之间的值 描述这个事件 (或事物) 接近/远离 某个状态 (如 False 或 True) 的程度.
考虑一个例子: 我们称 Axton 很强, 但究竟什么样才算是 很强, 什么样算是 比较强, 什么样算是 不太强? 在布尔逻辑中, 我们可以直接处理 是非分明 的场景, 比如判断一个人, Ta要么强, 要么根本不强. 但在模糊逻辑中, 很强, 比较强, 不太强 之间并没有严格界限, 换言之某个人能力的强弱不完全归属于一个类, 而是被一个称为 隶属度 的数值衡量的.
2. 模糊化 (Fuzzification)
模糊化 就是将逻辑的输入数值转换为各个分类集合的隶属度的过程, 输入数值和隶属度的关系被 隶属度函数 定义:
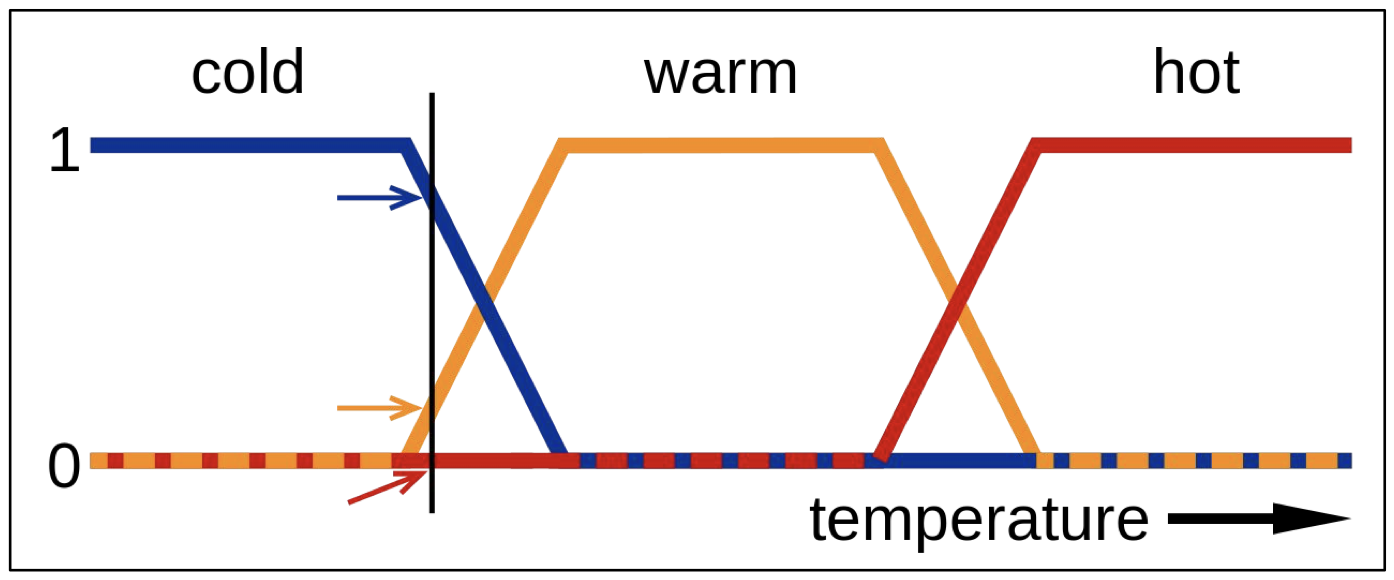
如在上图的隶属度函数中可以看到, 温度被人为地划分为 寒冷, 温暖 和 炎热 分类, 而这三个分类的隶属度函数分别在平面上以 蓝色, 橙色 与 红色 表示.
在该问题中, 温度由三个模糊集合组成, 且 给定温度数值, 该数值对应于不同模糊集合的隶属度由这三个集合的隶属度函数确定, 比如 $21$ 度 (对应图中竖线) 被视为 寒冷 的隶属度为 $0.8$, 视为 温暖 的隶属度为 $0.2$, 炎热 的隶属度为 $0$.
值得注意的是, 一个值可以同时属于不同的模糊集合.
3. 逻辑运算
模糊逻辑中的逻辑运算就是 模糊逻辑中, 分解出的各个隶属度的运算. 它们被定义为:
给定谓词 $A$, $B$, 则有:
-
最小隶属法 (
\[T(A \wedge B) = \text{min}(T(A), T(B))\]Conjunction): -
最大隶属法 (
\[T(A \vee B) = \text{max}(T(A), T(B))\]Disjunction): -
取反 (
\[T(\neg A) = 1-T(A)\]Negation):
4. 决策规则
在模糊化输入后, 我们需要构造规则, 应用模糊逻辑的运算将得到的隶属度组合计算, 以作为决策的依据.
一般地, 模糊逻辑的决策规则都为包含一系列逻辑语句的集合, 这些逻辑语句具备这样的结构:
\[\text{IF} ~<\text{antecedents}>~ \text{THEN} ~<\text{consequent}>~\]考虑讲义中提及的 The Basic Tipping Problem, 我们有下列规则:
- 给定前件规则
服务水平低或食材质量差, 限定结果只给很少的小费; - 给定前件规则
服务水平比较好, 限定结果只给一般水平的小费; - 给定前件规则
服务水平很高或食材质量很好, 限定结果慷慨解囊.
则我们可以将该模糊逻辑问题中如上描述的三条规则表示为:

值得注意的是, 如上面三条例子所描述的一样:
- 决策规则中的前件条件可以是某个由多个子条件组成的复合谓词公式, 如第一条规则中的前件条件实际上由两个子条件:
服务水低和食材质量差组成. - 决策规则中的前件条件可以是恰好由一个条件组成的复合谓词公式, 如第二条规则.
- 决策规则中前件条件的形式可以是某个谓词公式的取反, 如第三条规则.
对某个问题而言, 在给定所有的决策规则后, 我们需要使用上一节介绍的三种基础逻辑运算将这些规则转换为逻辑公式, 从而实现将给定的模糊条件转化为对应的 规则强度 (Rule Strength) 的功能.
5. 推断和去模糊化
在执行 推断 (Inference) 时, 我们的基本任务是基于 给定的模糊输入 确定 每一条规则给出的结果, 并 将这些不同的规则给出的结果综合起来.
在执行 去模糊化 (Defuzzification) 时, 我们的基本任务是给出一个数值作为最终的输出.
在模糊逻辑中, 执行 推断 的常用方法包括 Mamdami 模糊逻辑推理 和 Sugeno 模糊逻辑推理.
前者的输出仍是一个模糊集, 而后者的输出为由某个 单例隶属函数 (Singleton Membership Function) 定义的常数或线性函数.
单例隶属函数的特征为: 它只在其定义域上的某个点处具有非零函数值, 而在其他任何位置上的函数值均为 $0$. 我们下面详细描述两种推断方法的具体工作流程:
Mamdami 模糊逻辑推理
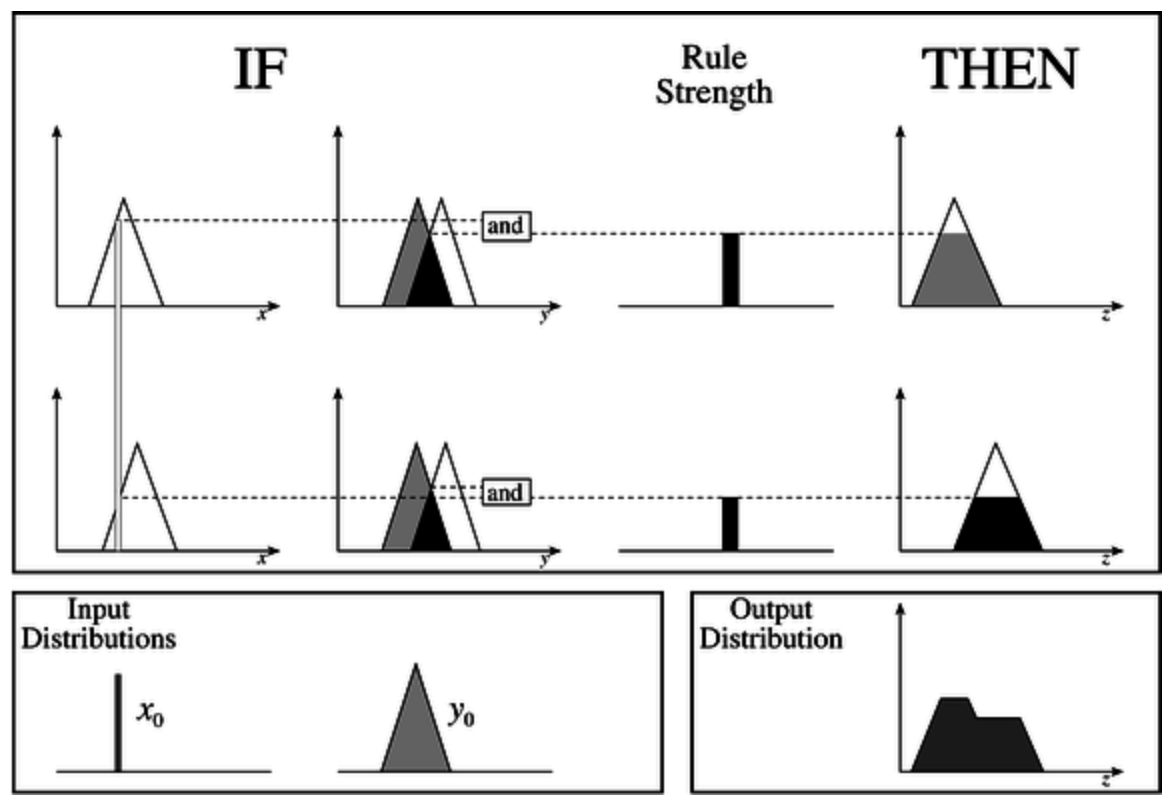
简要地说, 使用 Mamdami 模糊逻辑推理 计算模糊推断系统 (Fuzzy Inference System, FIS) 的输出需要下列的六个步骤:
- 确定给定问题的所有模糊规则 (
Fuzzy Rules) - 使用隶属函数将输入值模糊化.
- 基于模糊规则将 已经被模糊化的输入 结合, 进而计算出该规则在给定模糊输入下对应的 规则强度 (
Rule Strength). - 结合上一步中计算出的 规则强度 和 给定规则的输出隶属函数, 得出基于当前的模糊输入下该规则的 结果 (
Consequence). - 将来自所有规则的结果相结合, 从而得出输出分布 (
Output Distribution).
需要注意的是:
- 在第四步中, 结果 是通过将 给定规则的输出隶属函数 在 规则强度 的高度上 推平 得到的:
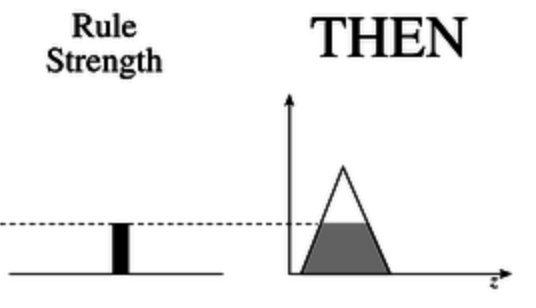
- 在第五步中, 绝大多数情况下 输出分布在定义域上任何点的值 都是 全体规则的输出隶属函数的析取 (也就是取并):
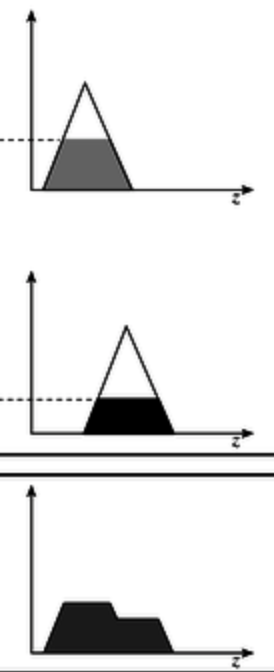
在得到输出分布后, 我们需要 去模糊化, 这一般是通过取 输出分布的函数和 $x$ 轴围成的图形的质心 得到的. 计算公式如下:
\[z = \frac{\sum_{i=1}^{q} Z_i \cdot u_c(Z_i)}{\sum_{i=1}^{q} u_c(Z_i)}\]其中 $q$ 为人为指定的划分份数, $Z_i$ 为 $x$ 轴上的对应划分处的值, $u_c(Z_j)$ 为输出分布在 $x$ 轴上某个位置上对应的函数值.
Sugeno 模糊逻辑推理
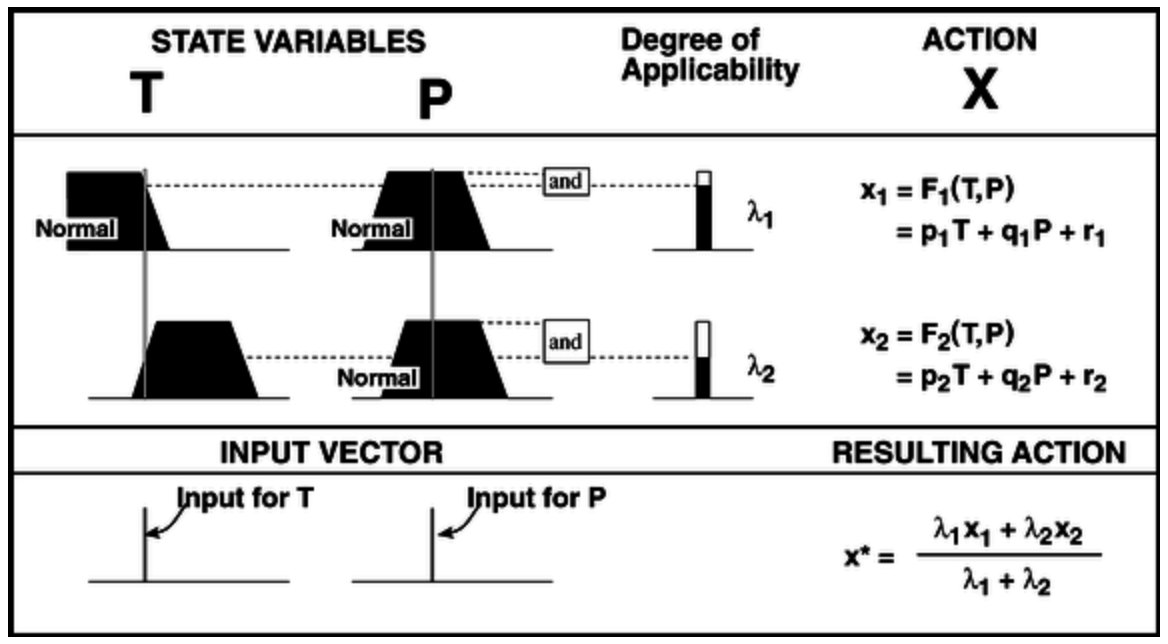
Sugeno 模糊逻辑推理 和 Mamdami 模糊逻辑推理 的流程基本类似, 主要区别在前者 不以隶属函数作为输出, 其输出是通过以 每条规则的输出隶属函数取极值时对应的 $x$ 坐标 为系数, 和 每条规则在给定的模糊输入下算出的, 对应的规则强度 取 加权平均 得到的.
如本题中, 计算 Sugeno 模糊逻辑推理 的算法就是:

Reference:
