知识表示
本章中我们将说明如何使用一阶逻辑表示现实世界中的知识. 在介绍 通用本体论 后, 我们将介绍如何表示 对象, 物质, 量度, 事件 和 信念, 然后讨论对应用在 高效类别推理 中的推理系统的设计.
5.1 本体论
我们使用 本体论 表示现实世界中的客观事物, 知识和通用概念. 在各种不同的情况下, 我们可能需要在 上位本体论 的框架下进行扩展, 使用一些特化的本体论表示具体的情形:
比如在对电路建模时, 我们可能需要忽略时间的概念, 假定信号是固定且不传播的; 或者, 我们在对模拟电路建模时可能需要考虑特定时刻的信号, 还要将电路中的导线长度和信号传播的延迟考虑在内.
对任何上述用于描述特殊情况的 特化的本体论 而言,它们是 有可能 收敛到一种通用的本体论的. 我们可以指出两个能够将 通用本体论 与 特化本体论 区分开来的特征:
- 通用本体论应该或多或少地具备应用于任何特殊领域的能力.
- 在任何足够特殊化的问题中, 通用本体论必须能够将来自不同领域的知识统一化.
类别和对象
由于 Agent 在与世界的交互发生在 个体对象 层面, 而推理发生在 类别 层面上, 因此在知识表示中, 将对象组织成类别是很重要的.
在确定了对象的分类后, 类别信息就可以用于对对象进行预测: 我们可以从 感知 推断出 某种对象的存在, 从 感知到的对象属性 进一步推断它的 类别归属, 然后用推断得到的类别信息对这些对象进行预测.
举例而言, 给定某台笔记本电脑, 从厚重的机身, 丑陋的缺口显示屏, 被涂黑的键盘区域和机身上意义不明的专用磁吸充电口, 我们就可以推断出这个对象是 $2021$ 年推出的最新款 MacBook Pro, 由此推断出这样的产品比较适合拿来垫桌脚.
在使用一阶逻辑表示类别时, 我们可以使用谓词表示某个对象的类别, 也可以将某个类别物化 (reify) 为一个对象.
我们通过在不同的类别之间构造 继承 (Inheritance) 关系来组织和简化知识库. 子类关系将类别组织成 分类系统 (Taxonomy) 或 分类层次 (Taxonomic Hierarchy), 比如生物学上的物种分类系统和图书馆的书籍分类系统.
一阶逻辑通过 在对象和类别之间建立联系 或 在类别的成员上量化, 从而描述 关于类别的事实. 举例而言, 它可以表示:
- 某个对象是某个类别的成员.
- 某个类别是另一个类别的子类.
- 某个类别中的所有成员均拥有某种属性.
- 一个类别的成员可以通过某些属性识别.
- 一个类别作为整体拥有某些属性.
我们接下来给出关于划分的一些概念:
定义 5.1.1 (不相交的)
称两个或以上的类别为 不相交的, 若他们没有公共成员.
定义 5.1.2 (完全分解)
若两个或以上的类别完全包括了父类中的所有成员, 称它们为一个 完全分解.
定义 5.1.3 (划分)
我们称不相交的完全分解为 划分.
对划分的表示语法如下:
# 可以使用谓词描述某个物体属于某个类别 (Cetegory):
Basketball(b)
# 可以通过将抽象的类别物化的方法标示某个物体的类别从属:
# 比如我们将 “篮球” 类物化为谓词 `Basketball`:
Member(b, Basketballs)
# 或者
b ∈ Basketballs
# 同时物化方法也可用来表示子类:
Subset(Basketballs, Balls)
# 或者
Basketballs ⊂ Balls
# 我们也可以通过描述物体的属性表示它在类别意义上的从属:
(b ∈ Basketballs) ⟹ Spherical(b)
Orange(b) ∧ Round(b) ∧ Diameter(b) = 9.5inches ∧ b∈ Balls ⟹ b ∈ Basketballs
物理构成
自然地, 某个对象可以是另一个对象的一部分, 这一关系用谓词 PartOf 表示. 需要注意, PartOf 关系是 传递的 和 自反的.
复合对象 的类别通常通过各部分之间的结构关系刻画. 我们可以定义类似于类别 Partition 关系的 PartPartition 关系: 一个对象由它的 PartPartition 中的各个部分组成, 则可看作这个对象从这些组成部分中得到了某些属性.
我们还可以定义 具有确定部分但没有特定结构 的复合对象. 举例而言, “这箱 MacBook Pro 2021 价值 $4000$ 美元”, 我们会倾向于认为这个价值归于箱子里包装盒而非盒子里的笔记本电脑的价值, 而非箱子本身的价值, 因为 集合 是抽象的数学概念, 它由元素组成但不具备 “价值” 这个属性.
对应的, 我们需要构造一个新概念: 束 (Bunch): 它描述了由一系列对象作为 部分 而组成的复合对象.
1
2
3
4
5
# 表示 “一部分”:
PartOf(Bucharest, Romania)
PartOf(Romania, EasternEurope)
PartOf(EasternEurope, Europe)
PartOf(Europe, Earth)
量度
显然在关于世界的科学理论和常识中, 对象具备 高度, 质量, 价值, 成本 等不同的属性, 我们赋予这些属性的值就被称为 量度 (Measures). 我们用 单位函数 (Units Function) 和数字作为参数来表示量度.
1
2
3
4
5
6
7
# 描述物体的量度属性:
Length(l) = Inches(1.5) = Centimeters(3.81)
Diameter(b) = Inches(9.5)
IQ(Axton) = 114514
# 描述对量度值之间的比较:
Difficulty(comp24011) > Difficulty(comp22111)
物体和物质
现实世界可以看作是由不可再分的基元对象 (如微粒子) 和由它们构成的复合对象组成的. 但在现实中存在一部分无法被简单地划分, 无法给出明确数量的对象, 例如水和气体, 我们称这类不服从明显的个体化 (Individuation) 的对象为 物质 (Stuff).
需要注意的是, 对象的一些属性是 固有的 (Intrinsic), 它们属于对象的每个实体而非整体: 当我们将物质切成两半时, 新得到的两半物质共享同样的固有属性集, 如密度, 沸点, 燃点, 颜色, 所有权等, 而类似重量, 长度, 形状等在划分时 无法保持不变 的 非固有属性 (Extrinsic) 属性就不同.
在定义中, 只包括固有属性的对象类就是 物质 或 物质名词, 而在定义中包含了任何非固有属性的类就是 可数名词.
1
2
3
4
5
6
7
# 描述不可数的物质:
b ∈ Butter ∧ PartOf(p, b) ⟹ p ∈ Butter
b ∈ Butter ⟹ MeltingPoint(b, Centigrade(30)))
# 注意: 描述物质时使用下列语法:
变量 ∈ 物质名 ⟹ 这一物质的属性
事件
我们可以使用 情景演算 表示 离散的, 瞬间的 动作. 考虑连续动作, 如无害化处理一台 MacBook Pro 2021, 情景演算可以告诉我们, 在这个动作之前我们有一台电子垃圾, 在这个动作之后我们得到了一系列可以被回收利用的电子元器件, 但它不能描述在这个动作期间发生了什么, 它也无法描述 在同一时间发生两个动作的情形: 如在等拆卸 MacBook Pro 完成的时候同时碾碎存有 Windows 11 源码的硬盘.
为了处理这种情况, 我们引入基于 时间点 而非 情景 的,称为 事件演算 (Event Calculus) 的形式体系.
流 和 事件 在事件演算中是被物化的. 在事件演算中, 流是一个描述了某种事实的对象, 但它并不会提供更详细的信息, 诸如 “这个事实是否成立”. 我们需要使用额外的谓词声称一个流实际上在某些时间点成立.
举例而言, 考虑流 StudyIn(Axton, UoM), 我们使用谓词 T(flow, timePoint) 说明这个流在某个时间点 t 上成立: T(StudyIn(Axton, UoM), t).
事件被描述为 事件类别的实例. 如 “Axton 从 Manchester 飞到 Paris 的事件 E1” 表示为:
随后, 我们使用 $\text{Happens}(E_1, i)$ 表示 事件 $E_1$ 发生在事件区间 $i$. 一个事件演算版本的完整谓词集如下图所示:

构造一个特别事件 Start, 这一事件描述 初始状态, 指出在起始时刻那些流被启动 (Initiate), 哪些流被终结 (Terminate).
同时定义谓词 T(event, t): 若某个流被 过去某个时间的某个时间启动且没有被任何干扰事件终止 (Clipped), 则这个流在当前的时间点为真. 反之, 若这个流 被某个事件终结且尚未被任何事件所恢复 (Restored) 则这个流在当前时间点不成立. 形式上的公理为:
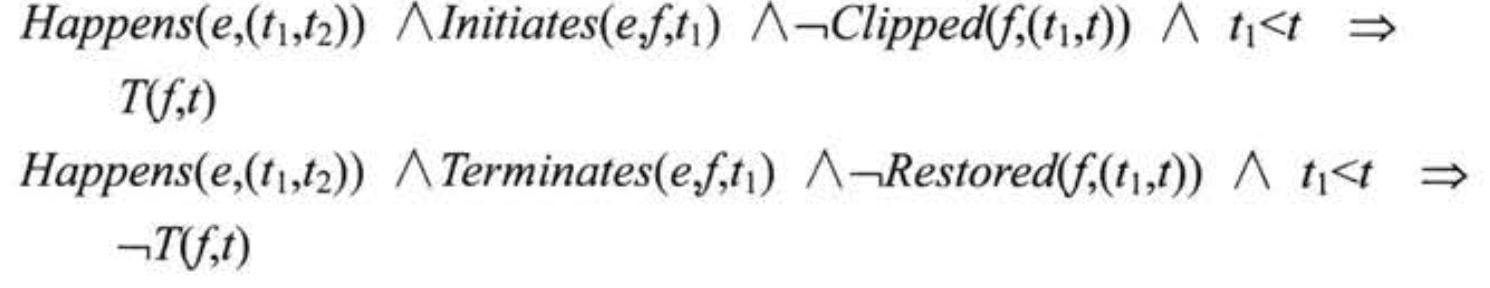
其中 Clipped 和 Restored 定义为:
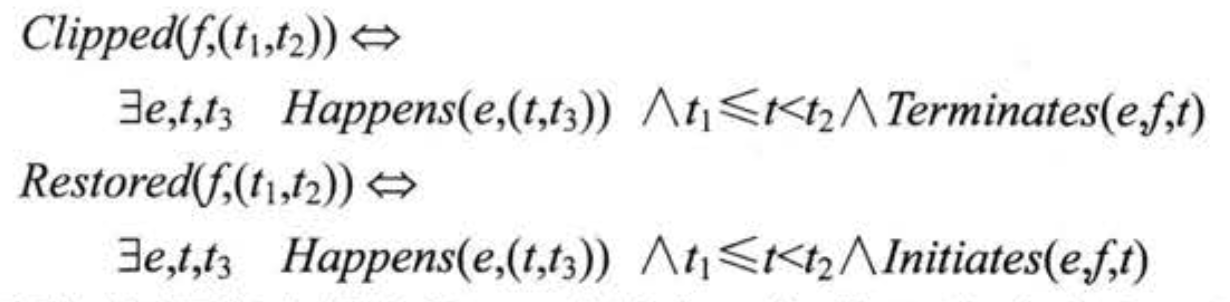
还可以将 T 扩展到事件区间中: 一个流在某个时间区间上成立, 当且仅当它在 这个时间区间内的每个点上 都成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# any process e that happens over an interval happens over any subinterval
(e ∈ Processes) ∧ Happens(e, (t1, t4)) ∧ (t1 < t2 < t3 < t4) ⟹ Happens(e, (t2, t3))
# 注意: 描述事件时遵循下列语法:
变量 ∈ 事件具备的一系列性质的合取
# 如: b ∈ Buyings ∧ Buyer(b, Mary) ∧ Seller(b, John) ∧ Price(b, GBP(400)) ∧ Item(b, bike)
# 或者:
变量 ∈ 事件名(事件中涉及的实体1, 事件中涉及的实体2, ..., 事件中涉及的物体1, ...)
# 如: b ∈ Buyings(Mary, John, GBP(400), bike)
而在谓词 T 中, 流和动作使用专门领域公理定义.
通过物化事件, 我们可以给它们增加 任何数量 的 任意信息. 通过扩展事件演算, 我们就可以表示 同时发生的事件, 外因事件, 连续事件 和其他的复杂事件.
过程
有一类事件具有 起始, 中途 和 结尾, 若从中间将这一事件打断, 事件的性质就会发生变化. 同时, 这样的事件类别具有不同的属性.
具有这种特征的事件类别被称为 过程 (Process) 或 流事件 (Liquid Event): 发生在一个时间区间内的任何过程 $e$ 也可以在该时间区间的任何子区间内完成.
时间区间
我们考虑两种时间区间: 时刻 (Moment) 与 时间 (ExtendedIntervals). 它们的区别在于, 时刻 的长度为 $0$, 也就是说它只有 零刻度.
随后我们取一个用来提供 绝对时间 的 时间标尺: 比如我们可以取格林尼治时区的 $1900$ 年 $1$ 月 $1$ 日 $00:00$ 为 $0$ 时刻, 构造函数 Begin, End, Time, Duration 分别用来: 取一个区间的最早时刻, 取一个区间的最晚时刻, 为某个时刻在给定的时间标尺上找出对应的刻度点, 以及给出开始时间和结束时间的差值.
流和对象
物理对象可以被视为是 一块时空片段, 由此它也可以被视为 泛化事件.
思维事件和思维对象
到此为止, 我们已经构造出了对于现实世界中具备物理实体的事物的表示方式, 由此 Agent 可以对它们产生和具备 信念 (或者知识), 并以此为基础演绎出新的信念. 下面, 我们需要考虑描述 思维对象 和 操控这些思维对象的思维模型 的模型.
首先从 命题态度 (Propositional Attitudes) 入手. Agent 对思维对象可以有一系列的 态度, 如 “确信“, ”了解”, “想要”, “打算”等, 我们使用 模态逻辑 表示这些态度.
常规的逻辑关注 单模态, 真值模态, 如 “命题 $P$ 为真”. 而模态逻辑包含以 语句 而非 项 作为参数的 专用模态算子, 如 “$A$ 知道 $P$” 用 $\mathbf{K}_{A}P$ 表示, 其中 $\mathbf{K}$ 就是用于知识的 模态算子. 该算子具有两个参数: 一个记为下标的 Agent, 和一个语句.
补充:


注意:
-
Equals()公式处的Before(i)应该改为Begin(i). -
During中的Begin(i), Begin(j)和End(i), End(j)是 严格不等关系.

Semantic Network:
- only Binary Relations
- n-ary assertions need to be break down into binary relations
Description Logics:
- Subsumption: check if one category is a subset of another one by comparing definitions
- Classification: Check whether an obj belongs to a category
-
Consistency: Whether the membership crteria are logically satisfiable

