线性时态逻辑
12.1 计算树
我们可以用 计算树 表示某个状态转换系统中所有可能的行为:
定义 12.1.1 (计算树)
考虑状态转换系统
\[\mathbb{S} = (S, \text{In}, T, \mathscr{X}, \text{dom}, L),\]并记状态 $s\in S$. 状态转换系统 $\mathbb{S}$ 的, 从状态 $s$ 起始的计算树的递归定义如下:
- 计算树的节点由 $S$ 中的状态所标记.
- 树的根节点由 $s$ 所标记.
- 对树中的每个节点 $s’$, 其任一子节点 $s’’$ 恰满足条件 $(s’, s’’) \in T$.
定义 12.1.2 (计算路径)
状态转换系统 $\mathbb{S}$ 的 计算路径 为 由一系列节点组成的序列 $s_1, \cdots, s_n$, 满足:
- 对任意 $i \in [n-1]$, 有 $(s_i, s_{i+1})\in T$.
- 若该序列是有限的, 则不存在任何 $s$ 满足 $(s_n, s) \in T$.
本质上, 某个状态转换逻辑的计算路径就是该逻辑中的某个最长的状态转换序列. 同时可知, 计算树和计算路径具备以下性质:
- 某个状态转换系统的计算路径恰为该状态转换系统计算树中的所有分支.
- 任何计算树的子树也是一棵计算树.
- 对任何状态转换系统 $\mathbb{S}$ 和状态 $s$, 一定唯一存在某个 $\mathbb{S}$ 中以 $s$ 为根节点的计算树.
12.2 线性时态逻辑
在本节中, 我们引入一种可以表示时态的逻辑系统, 用以表示计算树中某些分支的属性. 称这样的逻辑系统为 线性时态逻辑:
定义 12.2.1 (线性时态逻辑中的公式)
我们使用下列的规则递归地定义线性时态逻辑中的公式:
- $\top$ 和 $\perp$ 均被视为公式.
PLFD中的任何原子公式 (形如 $x=v$) 被视为LTL中的原子公式.- 若 $A_1, \cdots, A_n$ 为公式, 其中 $n \geqslant 2$, 则 $(A_1 \wedge \cdots \wedge A_n)$ 和 $(A_1 \vee \cdots \vee A_n)$ 也都是公式.
- 若 $A$ 为公式, 则 $\neg A$ 也是公式.
- 若 $A$ 和 $B$ 均为公式, 则 $(A \rightarrow B)$ 和 $(A \leftrightarrow B)$ 也都是公式.
- 若 $A$ 为公式, 则 $\bigcirc$, $\lozenge$, $\square$ 均为公式.
连接词和时态运算符的优先级和定义如下:
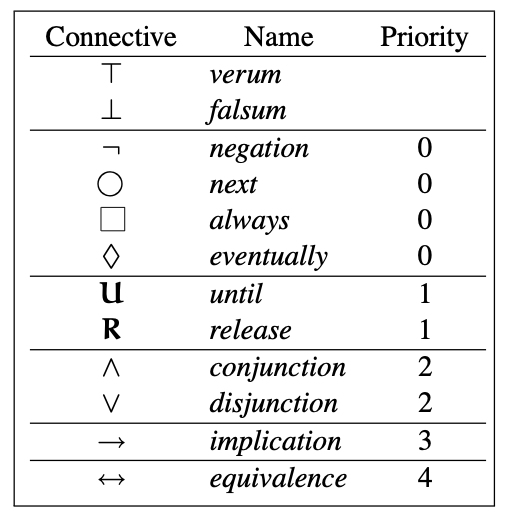
我们称 $\bigcirc, \lozenge, \square, \mathcal{U}, \mathcal{R}$ 为 时态运算符 (temporal operator).
LTL (线性时态逻辑) 中的公式的真伪性都是在定义在某个计算路径上的. 举例而言:
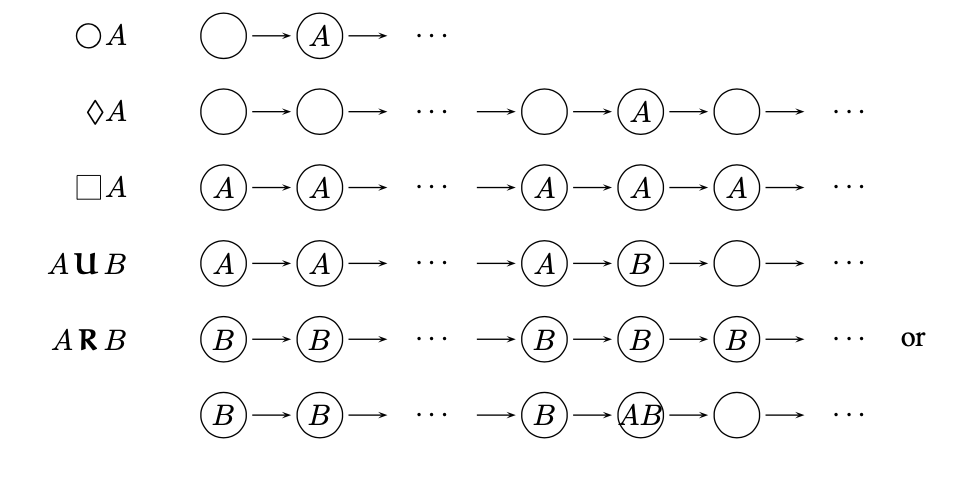
- 公式 $\square ~ A$ 表明, $A$ 在计算路径上 恒为真.
- 公式 $\lozenge ~A$ 表明, $A$ 在计算路径的 某一个状态上 为真.
- 公式 $\bigcirc ~A$ 表明, $A$ 在计算路径的初始状态 $s_0$ 的下一个状态 $s_1$ 上为真.
我们下面给出对 LTL 语义的形式化定义:
定义 12.2.2 (LTL 的语义)
记 $\pi = s_0, s_1, s_2, \cdots$ 为一个状态序列, $A$ 为一个
LTL公式. 我们递归地定义 公式 $A$ 在序列 $\pi$ 上为真 (记为 $\pi \vDash A$) 如下:首先约定, 对任意 $i \in [n]$, 定义 $\pi_i$ 为序列 $s_i, s_{i+1}, \cdots$. (在这个定义下, $\pi_0 = \pi$.)
- $\pi \vDash \top$ 且 $\pi \nvDash \perp$.
- $\pi \vDash x=v$ 若 $s_0 \vDash x=v$.
- $\pi \vDash A_1 \wedge \cdots \wedge A_n$ 若对任意 $j \in [n]$, 有 $\pi \vDash A_j$.
- $\pi \vDash A_1 \vee \cdots \vee A_n$ 若对任意 $j \in [n]$, 至少有一个 $j$ 满足 $\pi \vDash A_j$.
- $\pi \vDash \neg A$ 若 $\pi \nvDash A$.
- $\pi \vDash \bigcirc ~A$ 若 $\pi \vDash A$.
- $\pi \vDash \lozenge ~A$ 若对某个 $i \in [n]$, 满足 $\pi_i \vDash A$.
- $\pi \vDash \square ~A$ 若对任意 $i \in [n]$, 满足 $\pi_i \vDash A$.
- $\pi \vDash A~\mathcal{U}~B$ 若对某个 $k \in [n]$, 我们有 $p_k \vDash B$ 且 $p_0 \vDash A, \cdots, p_{k-1} \vDash A$.
- $\pi \vDash A~\mathcal{R}~B$ 若对任意 $k \in [n]$, 要么 $\pi_k \vDash B$, 要么存在 $j < k$ 使得 $\pi_j \vDash A$.
注意:
-
线性时态逻辑中的公式 $A, B$ 是等价 (记为 $A \equiv B$) 的, 当且仅当对计算树中的 任何 计算路径 $\pi$, $\pi \vDash A$ 当且仅当 $\pi \vDash B$.
-
我们一般将 “线性时态逻辑公式 $A$ 在路径 $\pi_i$ 上为真” 简称为 “线性时态逻辑公式 $A$ 在状态 $s_i$ 上为真”.
线性时态逻辑中时态运算符的语义表示如下:

12.3 时态公式的等价性
时态公式中时态运算符的等价性如下图所示:

注意最后一条规则: 它说明, 实质上 $\mathcal{U}$ 可等价表示任何时态运算符.
- Every Computation Tree is a binary tree –
FALSE - If an LTL formula is true on a path then its negation is false on this path. –
TRUE - If an LTL formula is true on all paths then its negation is false on all paths. –
TRUE - If a formula F does not contain temporal operators then F is true on a path s_0,s_1,..,if and only if F is true in s_0. –
TRUE - For every LTL formula there is an equivalent formula that does not contain operators [] and <>. –
TRUE
