函数式编程导论
在本节中, 我们将以 Haskell 为例了解 函数式编程 的思想, 基本特征和方法.
下面首先粗略地给出 函数式编程 的基本特征:
- 将 所有的函数 (
Function) 视为 变量 处理: 允许 匿名函数 的声明, 允许将函数 作为其他函数的输入或输出. - 将 程序中的函数 视为 数学中函数 (映射): 其输出 只和它的输入有关, 如果两个函数的输入输出相同则 (在
Haskell中) 它们 等价且可被彼此替换; 由此函数还不能执行任何意义上的 副作用.
1. Haskell 中的基本定义
首先考虑 Haskell 中对变量/表达式/算式, 以及函数的基本定义:
对变量, 表达式和算式的基本定义方法
Haskell 中 任何表达式和函数 都被统一视为 变量.
1
2
3
4
5
6
7
8
9
b = False || (False && True)
n = 1 + 7
b2 = n /= 8
b3 = (0,0) == (0,0)
v = 7 * (if b then 5 else 6)
上面例子中的 v 实际上是一个表达式, 但在理解时需要将其理解为整数类型的变量, 只不过该变量的实际值随另一个 (布尔型) 变量 b 而定.
对函数的基本定义方法
在 Haskell 中, 基本的 函数定义方法 包括 使用等式定义函数 和 使用模式匹配 (实际上也就是不同的) 定义函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
-- defining a function by an equation
add7 n = n + 7
-- defining a function by pattern matching
-- change the order and see what happens!
small 0 = True
small 1 = True
small n = False
-- defining a function on pairs by pattern matching
-- gives us more interresting examples
addUp (0,n) = n
addUp (m,0) = m
addUp (m,n) = m + n
-- we can also use _ to denote we don't care this input
first (e,_) = e
注意, 虽然 addUp 函数看上去是一个 接收了两个输入的二元函数, 但实际上应当将其视为一个 接受单个参数的一元函数, 只不过其唯一的输入恰好是一个包含了两个子元素的元组.
我们可以进一步地利用类型匹配 递归地 定义函数, 如下面例子中分别定义了 计算斐波那契数列的递归规则中的 Base Case 和 Step Case.
1
2
3
4
5
-- defining a reursive function
fib 0 = 0 -- base case
fib 1 = 1 -- base case
fib n = fib(n-2) + fib(n-1) -- step case
对高阶函数的定义
回顾高阶函数概念本身的定义: 我们称至少输入和输出中有一项是函数的函数为 高阶函数.
我们首先考察 Haskell 中一个 隐式定义高阶函数 的例子:
1
2
3
4
5
6
7
8
-- this function takes a number and returns
-- the function which adds that number to
-- its input
addConst n m = n + m
-- we can test it by evaluating it at 3
-- and seeing what function we get
addThree = addConst 3
实际上它等同于下面所示的 addConstB:
1
2
3
-- we can use anonymous functions to make it
-- obvious that this returns a function
addConstB n = \m -> n + m
进一步地, 我们可以使用 匿名函数 更清晰地定义高阶函数:
1
2
3
-- indeed, we can define a function explicitly
-- using anonymous functions, rather than equations
addConstC = \n -> (\m -> n + m)
注意 Haskell 中的 Shadowing:
1
2
3
4
5
6
7
8
9
-- note: when a variable is used, it refers to
-- the definition closest to the usage, so
-- the following returns the identity function, not
-- a constant function. This is called 'shadowing'
h n = (\n -> n)
-- but the following expression defines a function
-- which returns a constant function.
h2 n = (\m -> n)
和其他常规函数一样, 我们也可以递归地定义高阶函数:
1
2
3
4
5
-- we can define recursive higher-order functions
-- just like any other functions
repFromZero 0 f = 0
repFromZero n f = f(repFromZero (n-1) f)
其他有用的变量定义方式
case 语句
我们可以使用 case 定义不同条件下函数的输出, 可以立即注意到, 它可被用于定义函数的 递归规则:
1
2
3
4
5
6
7
8
9
10
11
12
-- recall the definition of small above:
small 0 = True
small 1 = True
small n = False
-- we define a function which returns
-- True when it's argument plus one is small
-- using a case expression:
smallB n = case n + 1 of
0 -> True
1 -> True
n -> False
guard 语句
我们也可以使用下面展示的 guard expression 语法定义条件语句:
1
2
3
4
5
6
7
8
9
10
11
12
13
-- a guard expression lets you define a value
-- differently in different situations, defined
-- by boolean expressions.
-- It can also contain a 'where' clause to define
-- a repeated part of the boolean conditions.
sideOfFive n
| d > 0 = 1
| d < 0 = -1
| otherwise = 0 -- represent final/default case
where d = n - 5
注意我们用变量 d 代替了表达式 n-5.
let 关键字
我们可以使用 let 关键字在表达式 行间 定义变量值且应用在表达式中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
-- a 'let' expression allows us to name
-- a value and use it in an expression
-- it is useful for making long formulas
-- more readable
y = let x = 10 + 10 -- just a local definition of x
in x + x
-- the let expression also **exhibits shadowing**:
-- the innermost let below is the one used for the
-- meaning of x.
-- Note that the below is not an intruction to
-- 'change' x from 10 to 20. In Haskell nothing
-- ever changes! We are just saying that locally
-- we want x to be defined in various ways.
z = let x = 10
in
let x = 20
in x
注意在 z 的例子中, 实际上 x 先被定义为了 $10$, 然后在 内层的表达式 中被暂时改为了 $20$, 此处体现了 shadowing: 最内层表达式中的 x 优先和离自己最近的赋值语句匹配.
最后考虑一个更复杂的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
-- now we can see that functions do behave just like
-- ordinary values in at least one way:
-- at the point the definition of f below, the local
-- definition of x is 5, so f is defined to be the
-- constant function 5.
-- We don't need to worry about local definitions
-- of x in other parts of the code to understand
-- what f does.
w = let x = 5 in
let f = \n -> x in
let x = 6 in
f 0
注意此处 f 中对 x 的定义取 $5$ 不取 $6$ 的主要原因其实不是 shadowing, 而是由于在定义了 f 内层里对 x 的重新定义不会对外层中 f 里 x 的定义产生任何影响.
其他的一些常见错误
下面讨论一些在定义变量时常见的错误.
- 模式匹配中不定义默认情形:
1 2 3 4 5
-- not defined for all inputs -- this causes a runtime error oops True = True --try running main = print (oops False)
-
递归定义函数时构造用不终止的循环或不构造有效的
Base Case:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
-- this recursive function is badly defined and will -- run forever on inputs other than 0 eep 0 = 0 eep n = 1 + eep n -- printing yikes will cause Haskell to run forever -- searching for a number x such that x = x + 1 yikes = let x = 5 in let x = x + 1 -- the following will also run forever: -- even though there are plenty of values equal -- to themselves, the defintion gives us no clue -- about which one the programmer wanted yikesB = let x = x in x
相关题目解析
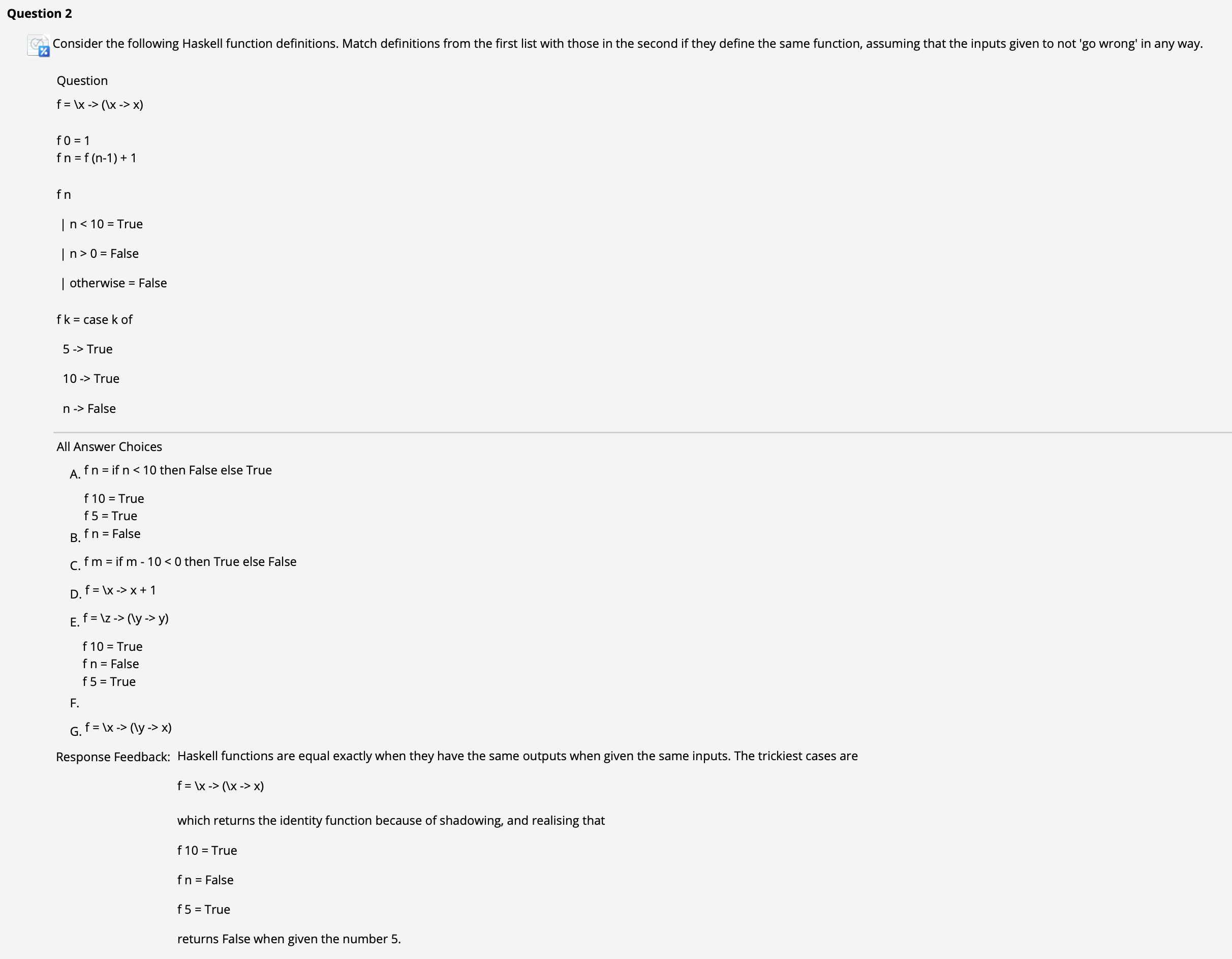
此题中唯一重要的问题是: 函数 f = \x -> (\x -> x) 的实质.
回顾此前讲过的, shadowing 的规则, 我们知道在函数 f 内层真正作为输出的 x 实际上 是和内层的 x 相匹配的, 因此它应该等价于 选项 E: f = \z -> (\y -> y).
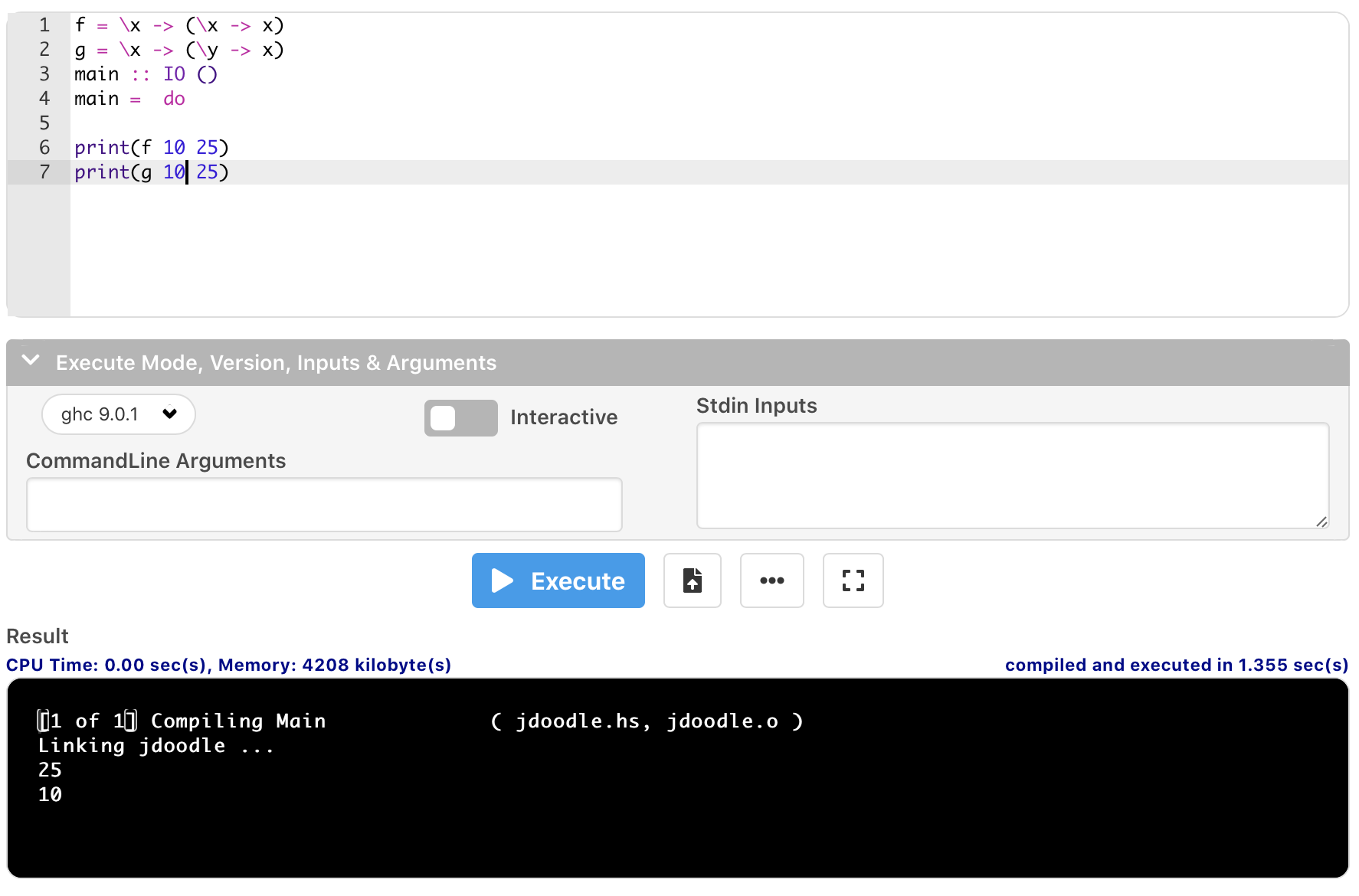
2. Haskell: 类型系统
在 Haskell 中, 任何表达式均具备类型, 且对类型的检查发生在 编译阶段.
Haskell 中的类型限制和自动类型推断
1
2
3
4
5
6
7
8
-- we can explicitly give the type of a function
f :: Int -> Int
f x = x + 1
-- Note: Int is fixed precision, Integer unbounded
-- We also have Float, Double
fd :: Double -> Double
fd x = x + 1
如上面的例子, 在指定函数输入输出的数据类型后, 如果提供了类型不正确的变量, 就会因为和数据类型规定冲突而无法编译.
若我们 不明确提供变量的数据类型, 则它们的数据类型会由 编译器推断得出.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
-- In Haskell, every expression has a type
-- How come last week we didn't have to
-- delcare them? Haskell infers types
-- we don't give explicitly E.g.
j x = True
-- What is the type of j?
-- We can give it several types, like
j :: Bool -> Bool
j :: Int -> Bool
-- Note we can't give it type Bool -> Int!
-- But the original has a strange feature:
main = print(j 1 && j True)
-- Is this 'dynamic typing'? No it is called
-- 'parametic polymorphism'. We can use
-- type variables to indicate that something
-- works for all types!
j :: a -> Bool
在上面的例子中, 实际上函数 j 在未经声明输入类型, 并在两个地方分别应用了 以整数为类型的输入 和 以布尔型为类型的输入 时, 会触发 通用类型 (General Type) 机制, 编译器通过 自动类型推断 得出该函数的输入可能具有至少两种不同类型, 因此将其输入的类型设为 动态类型: 该函数接收 任何类型的输入, 并输出布尔型数据.
Haskell 中的类型构造器 (Type Constructor)
此前我们介绍过可以使用 Haskell 中的 二元元组/变量对 向函数中 “同时传递两个变量”, 而这也是在 Haskell 中构造 自定义数据类型 的方式之一: pair of types => type of pairs.
1
2
3
4
5
-- We can use type constructors to make
-- more complicated types out of other types!
-- e.g. the type of pairs
sumPair :: (Int, Int) -> Int
sumPair (x,y) = x + y
进一步地, 我们可以定义 接受函数作为输入, 并以函数作为输出的高阶函数 的, 输入输出的数据类型:
在下面的例子中, 首先定义的是一个 接受类型为: “输入整数, 输出布尔型的函数”, 输出类型为 “布尔型” 的高阶函数:
1
2
3
4
5
6
7
8
9
-- Similarly, given two types we can construct
-- the type of functions from one to the other
atTen :: (Int -> Bool) -> Bool
atTen f = f 10
main = print(atTen (\x -> True))
-- note this is an example of type inference!
-- we could write explicitly
main = print(atTen ((\x -> True):: Int -> Bool))
其次定义的是一个以 相同类型的函数作为输入/输出的, 通用类型的高阶函数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
-- We can use more than one type variable to indicate
-- which inputs have to have matching types
myApp :: (a -> b) -> a -> b
myApp f x = f x
main = print(myApp (\x -> True) 10)
-- note that it would also be correct
-- to give myApp a less general type e.g.
myApp :: (Int -> Bool) -> Int -> Bool
-- which still lets the example work:
main = print(myApp (\x -> True) 10)
-- but also
-- myApp :: (a -> a) -> a -> a
-- which doesn't! But it works for e.g.
-- main = print(myApp (\x -> 11) 10)
-- where the types are all the same
-- Note that we can't have
-- myApp :: (a -> b) -> b -> a
-- because this doesn't match what happens
-- in the definition: we can't apply a funtion
-- of type (a -> b) to an input of type b!
Haskell 中的代数数据类型 (Algebraic Datatypes)
所谓的 代数数据类型 是指通过形如 代数运算 的方式从基本数据类型或更简单的自定义数据类型 组合而成 的数据类型:
- 认为 “选择型数据类型” (如
A|B型, 表示 “A或B”, 以及枚举) 对应 代数和 (Sum) - 认为 “组合型数据类型” (如
AB型, 表示 “A和B”), 对应 代数积 (Product).
Haskell 允许我们使用 data 关键字构造 用户自定义数据类型.
首先我们可以构造 枚举数据类型:
1
2
3
4
5
-- ALGEBRAIC DATA TYPES
-- we can make our own types by using the 'data'
-- keyword. The simplest are enumerations, which
data SwitchState = On | Off
利用自定义的枚举数据类型, 我们可以利用 模式匹配 定义函数:
1
2
3
4
5
6
7
8
9
10
11
-- we can define functions by pattern matching
toggle On = Off
toggle Off = On
isOn On = True
isOn Off = False
-- main = print(isOn (toggle On))
-- Note we can't do `main = print(toggle Off)`
-- because we haven't told Haskell how to print
-- a value of this type. (How to print "on"?)
自然地, 我们还可以基于现存的基本类型构造出新的自定义数据类型:
1
2
3
4
5
6
7
8
9
-- we can also attach data from existing types
data MyIntPair = IntPair Int Int
mySumPair (IntPair x y) = x + y
main = print(mySumPair(IntPair 3 6))
-- we can also ignore some fields of a constructor
myfst (IntPair x _) = x
main = print(myfst (IntPair 1 2))
我们可以基于现存的基本数据类型构造代数数据类型:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
-- we can combine the ideas of enums and data
-- fields
data BoolOrInt = Abool Bool | Anint Int
-- This is called an 'algebraic datatype'
intval :: BoolOrInt -> Int
intval (Abool True) = 1
intval (Abool False) = 0
intval (Anint x) = x
opposite :: BoolOrInt -> BoolOrInt
opposite (Abool True) = (Abool False)
opposite (Abool False)= (Abool True)
opposite (Anint x) = (Anint (-x))
main = print(intval(opposite (Abool False)))
补充: Maybe StackOverflow
还可以用 递归的方式 定义代数数据类型:
1
2
3
4
5
6
7
-- Algebraic datatypes can be recursive. This
-- is useful for recursively defined data structures
data MyList a = Empty | Append a (MyList a)
myHead Empty = Nothing
myHead (Append x l) = Just x
main = print(myHead (Append 10 (Append 11 Empty)))
Haskell 中的列表语法
下面讨论 Haskell 内置的列表数据类型的语法:
我们通过在变量左右加入中括号 [] 声明列表:
一般表示 List 变量的方式形如 1:2:3:[], 而 Haskell 当然支持更阳间的列表语法糖, 因此我们可以用这样的方式表示列表: [1, 2, 3].
1
2
3
4
5
6
-- define a function take an integer list as input type
myIntHead :: [Int] -> Maybe Int
myIntHead [] = Nothing
myIntHead (x:xs) = Just x
main = print(myIntHead ([1, 2, 3])))
下面考虑更复杂的例子:
1
2
3
4
5
6
myHead :: [a] -> Maybe a
myHead [] = Nothing
myHead (x:xs) = Just x
-- String is defined as a list containing chars
main = print(myHead ("Hi!"::[Char]))
同时, Haskell 提供了一系列对于 数值列表 的简易语法:
1
2
3
4
5
6
-- quick defining numeric list:
[1, 3..10] <=> [1, 3, 5, 7, 9]
-- construct new list containing data from two disjunct lists, combination:
l = [(w, n) | w <- ""Hi!, n <- [1..3]]
-- result is: [('H', 1), ('H', 2), ('H', 3), ('i', 1), .., ('!', 3)]
相关题目解析

3. 严格性
在本节中我们讨论 如何在 Haskell 中定义函数, 并讨论在定义函数时可能出现的常见错误. 我们首先从常见的, 数值上的错误 开始.
Haskell 中的数值错误 Error Values
此前我们已经了解了在定义 Haskell 函数时由于 模式匹配时不匹配默认类型 和 构造递归结构时不构造 Base Case 导致循环只能无限执行 这两类常见的函数定义中的错误.
由于在 Haskell 中 万物皆函数, 因此最简单的 Haskell 函数错误就是: 定义某个变量 $x$ 为它自己: “x=x”, 然后尝试输出这个变量.
在这一语境下实际上 $x$ 被视为函数, print() 实际上执行的是对函数的调用, 又因为函数循环调用自身, 因此程序执行 永不能停止.
实际上, Haskell 中就有一个内置谓词 bottom, 它的定义就是:
1
bottom = bottom
因此, bottom 被用来指代 永不能成功完成的计算.
我们称 会检查作为输入的程序参数的正确性 的 Haskell 函数是 严格的 (Strict).
为了检查给定的函数是否为严格的, 我们可以利用 Haskell 内置的 error 谓词 人为定义具有输出功能的, 可用于debug 的 错误变量:
1
2
3
4
5
eInt :: Int
eInt = error "Hang on..."
eBool :: Int
eBool = error "Hang on..."
在将 错误变量 作为函数的参数传入时, 如果函数在执行时的某一步 evaluate 了它, 程序就会终止并在控制台输出相关的错误信息:
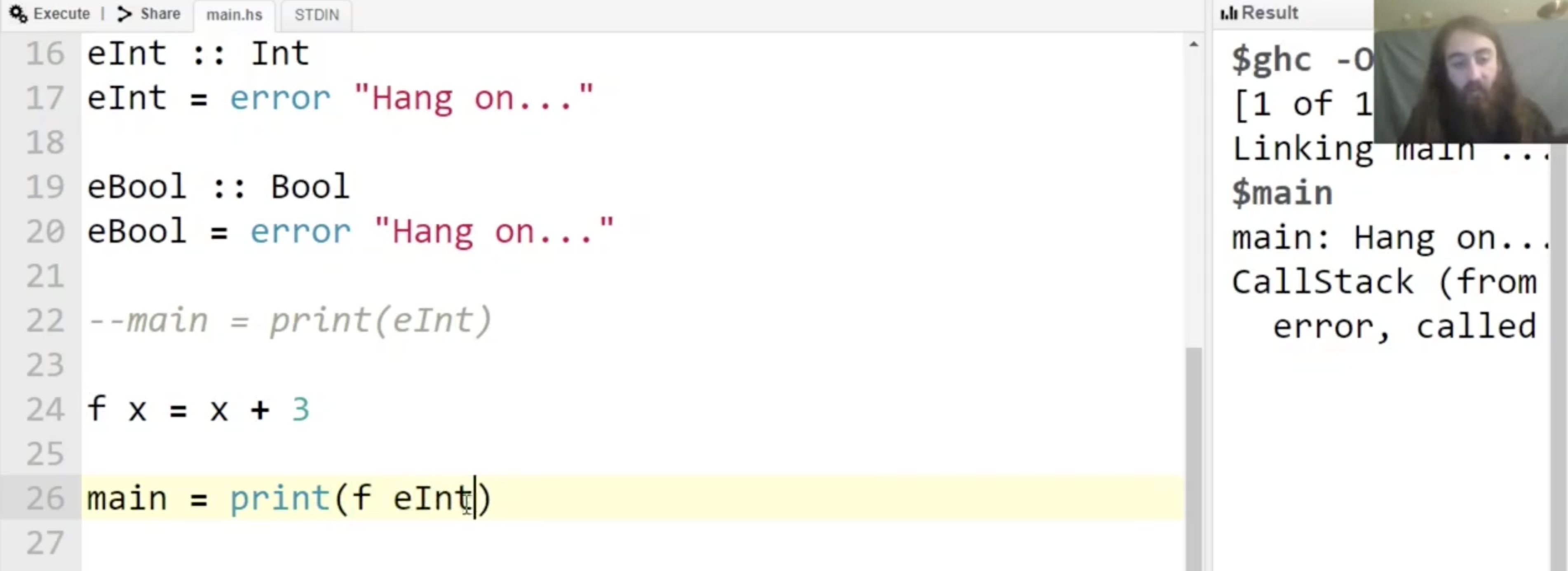
可见函数 f 在执行时会 evaluate x, 因此会触发错误并在右侧的控制台里输出我们指定的错误信息 “Hang on…”.
而下列的函数即使接受任何输入都不会出错, 因为它 在任何情况下都不会 evaluate 它的任何输入:
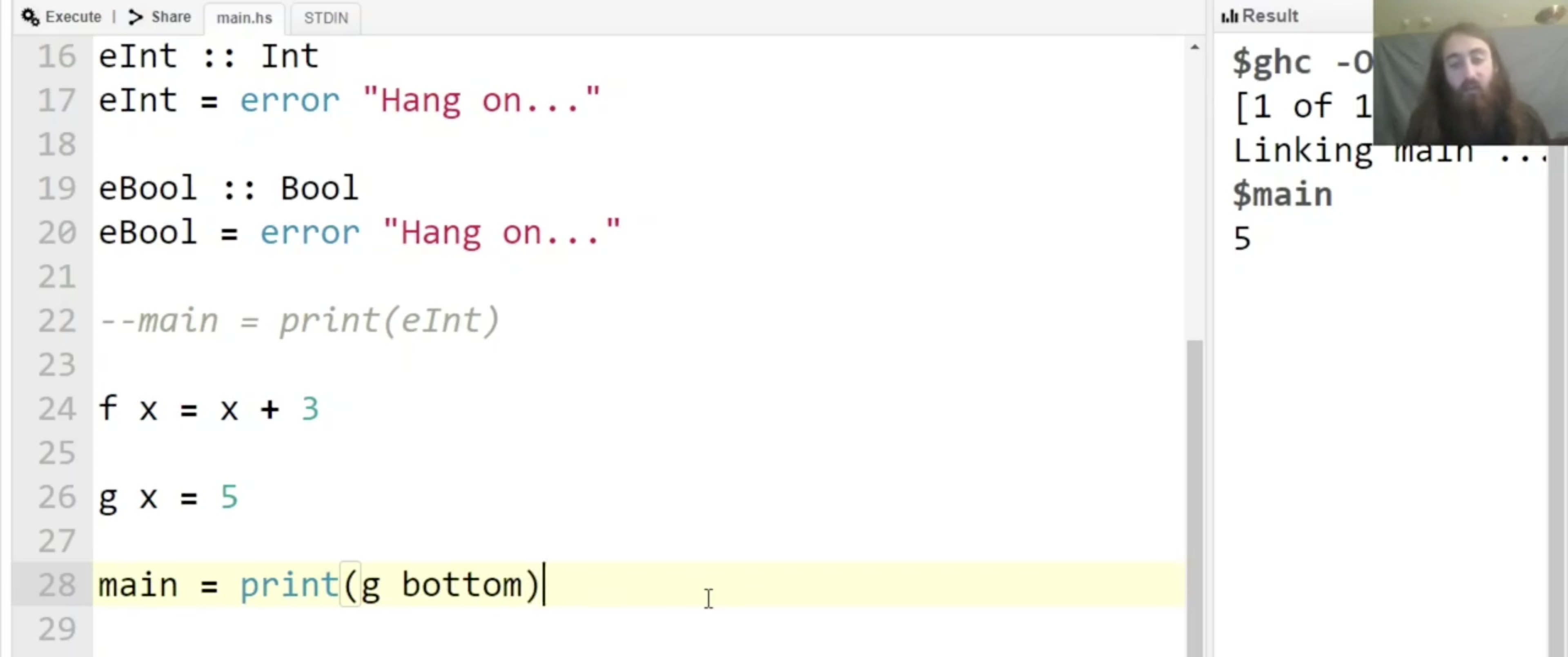
而我们通过实验可以发现, Haskell 中的二元乘法 * 对于任何一个输入都是 strict 的.
在错误中推理
我们下面说明在 Haskell 中, 对某些参数 strict 的函数在 evaluate 它的参数时的一些特性.
首先, 对于任何 strict 的函数 (也就是如果接收错误输入可能导致错误的函数), 该函数 可能返回的错误类型 实际上是 全体可能的错误类型组成的集合 中的 任何一个, 编译器在检查时如果发现错误, 返回的错误类型/错误提示信息 是集合中的任何一个, 具体返回哪一个取决于 编译模式, 编译器自身实现甚至计算机的当前运行状态, 它是 非确定的.
因此, 我们如果执行下列的代码, 在大多数情况下会发现编译器返回的只是乘法 * 中 第一个元素的错误信息, 但这 并不能说明乘法不是可交换的 (Commutative) 的.
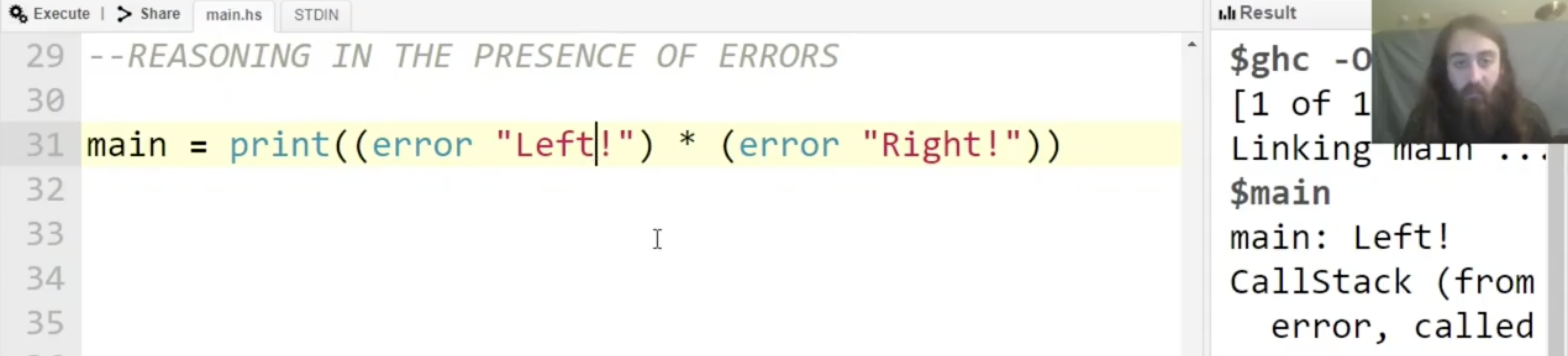
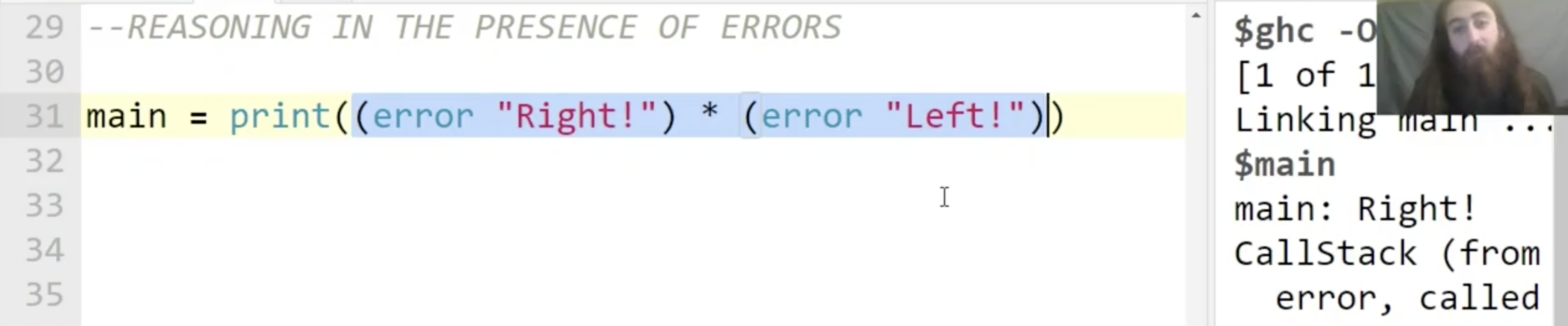
不过我们确实可以在乘法的基础上实现一个 只对一个变量严格, 对另一个不严格 的 不满足交换律 的乘法:

可看出 stimes 总是会优先检查第一个元素是否出错, 因此它对于第一个参数是严格的, 对第二个参数不严格. 同时, 在两个输入都正常的情况下返回的总是 m * n, 因此它也是不满足交换律的.
注意在此处我们可以使用 “`” 将函数作为 算子 的形式插到两个参数中间.
此外, Haskell 中的 逻辑运算符 是 不具备交换性 的, 它会遵从短路特性优先从左到右地检查每个变量. 如: 对于 a && b, 如果 b 是一个 error value 而 a 是 $0$, 则它会直接返回 $0$.
下面讨论问题: 这样的两种 pair 是不是本质上相同?

通过下面两个函数的检测, 我们可以发现他们是被认为 不相同 的:

在 Haskell 中, strangePair 被视为 包含两个 error 的二元组, 而 ePair 被视为 一个 error.
因此, 对 h 而言, 由于它 只接受形状为二元组的输入, 因此接收 ePair 时会返回错误, 而接受 strangePair 时可以正常输出 $42$.
对 j 而言, 由于它对 参数的形状 没有限制, 因此对两种不同的输入它都能正常执行输出 $10$.
同时, 这样定义的变量 ePairb 和 ePair 也是不一样的. 前者是包含两个相同 error 的二元组 (因为 ePair 本身是 error, 因此把它当成元组, evaluate 它的第一个或第二个元素的时候自然会返回同样的 error), 而后者只是一个 error. 这样的话, 在一些情况下 即使程序中有一部分存在错误, 只要这部分错误不被执行, 程序还是可以被正常执行.
1
ePairb = (fst ePair, snd ePair)
Haskell 中的这一特性称为 对类型形状 (Spine) 的严格性 (Strictness).
无限的数据结构
回顾此前介绍的 代数数据类型 的定义: 通过 选择 和 组合 构造出的自定义数据类型. 我们下面将要介绍, Haskell 中结合代数数据类型和对数据类型的懒惰特性 (数据可以是无限大的, 只有在需要它的时候才会被计算出来) 后所产生的可能性.
首先说明 Haskell 对数据类型严格性判别的懒惰特性: 从下面的代码段可以看出:
mylen对输入的spine不严格, 对输入的元素中的第一个也不严格, 但对输入的元素中剩下的部分的spine严格 (必须得是list).mylen并不会evaluate不需要被处理的元素, 也就是作为输入的列表里存储的任何元素.

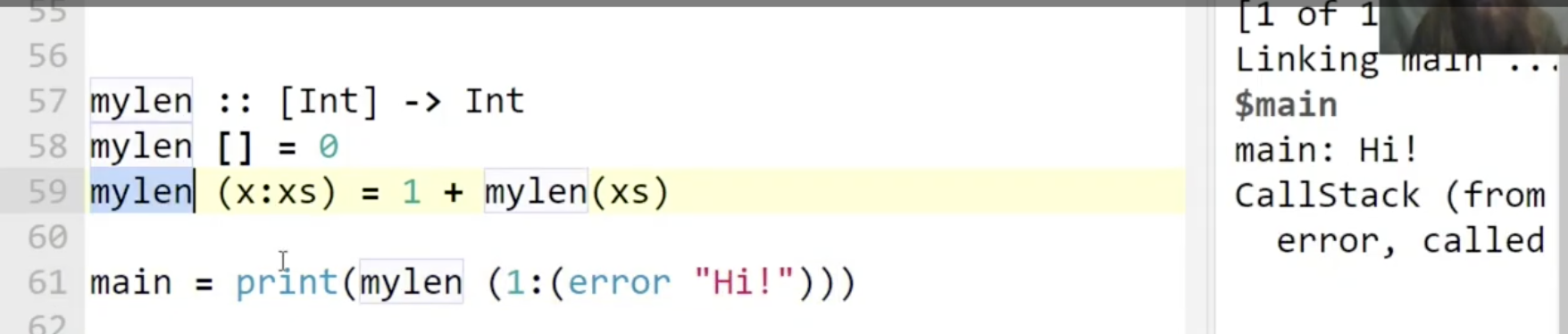
可以看出当输入为 1:(error "Hi") 时, 由于 mylen 会检查输入中去掉第一个元素后剩余的部分是否为列表, 因此此时会触发错误.
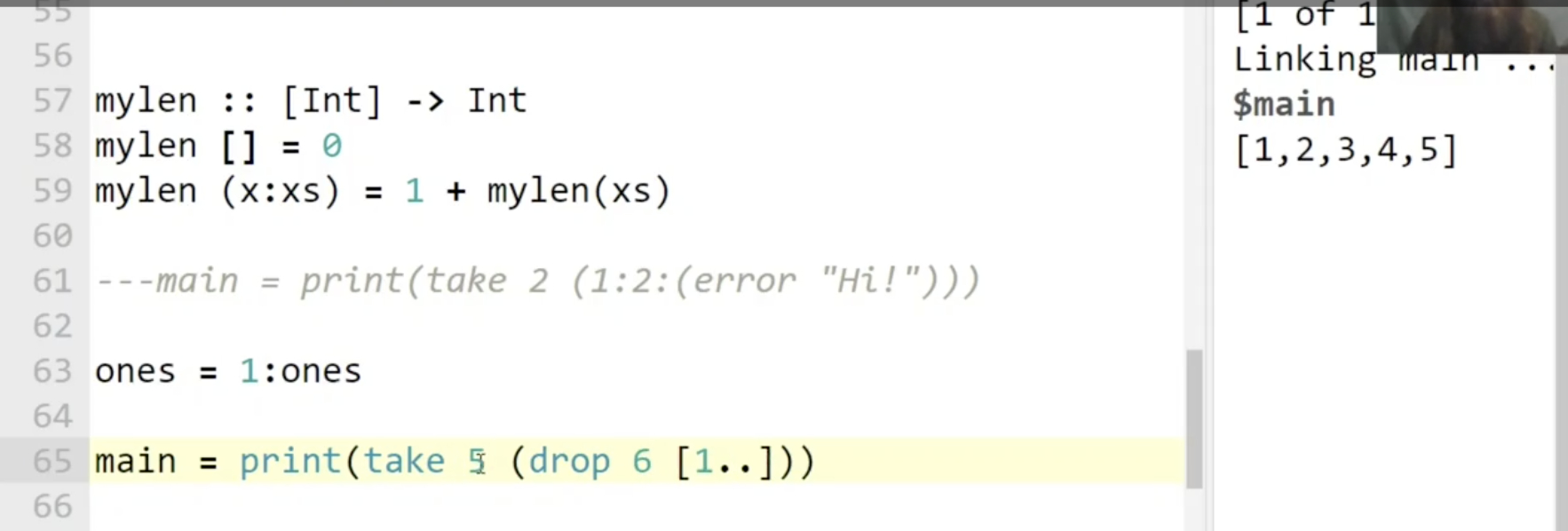
同时可知, 用于提取出列表中前 $k$ 个元素的内置谓词 take 是对输入的前 $k$ 个元素严格, 对剩余的 不严格 的:

下面说明 Haskell 在生成数据时的懒惰特性. 考虑构造下图所示的一个 无穷大列表, 虽然尝试将其整个输出时会出现问题, 但我们可以取这个无穷大列表中 任何位置上有限长的一段, 此时 Haskell 会自动计算出所需要的那一段返回给我们:

注意上图中右侧的控制台输出.
我们也可以应用 Haskell 中构造无限列表的语法糖 .. :
最后展示一个比较复杂的, 构造包含了全体自然数的列表的例子:
1
nats = 0 : [n+1 | n <- nats]
上述代码中 [n+1 | n <- nats] 的意思是: 从 nats 中依次取出 $n$, 然后加 $1$ 后放进列表中. 由于我们规定了 nats 中第一个元素是 $0$, 自然第二个是 $0+1$, 第三个是 $1+1$, … , 如此构造出包含全体自然数的列表.
下面介绍利用无限数据结构的高级操作:
在 Haskell 中, 内置算符 !! 用来对列表 indexing, list !! n 的结果就是从列表 list 中取出第 n+1 个元素, 因为列表编号从 $0$ 开始.
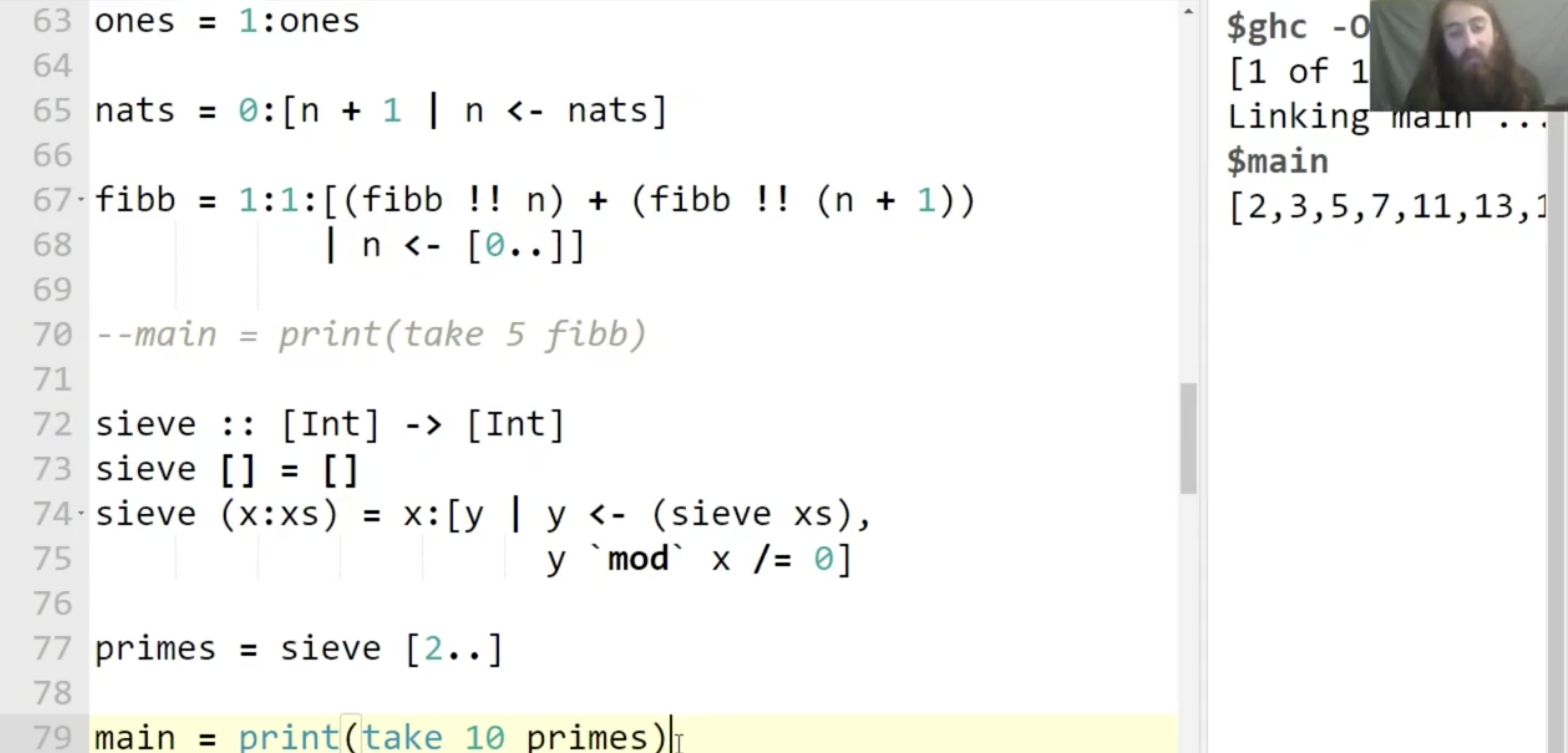
利用这个算符, 就可以构造出非常复杂的, 递归定义的列表. 如下面构造斐波那契数列的例子:
1
fibb = 1:1:[(fibb !! n) + (fibb !! (n+1)) | n <- [0..]]
注意在上面的例子中展示了, 我们实际上可以 在列表的内部对其本身 indexing…
最后以一个 过滤出全体素数 的例子结尾:
相关习题解析
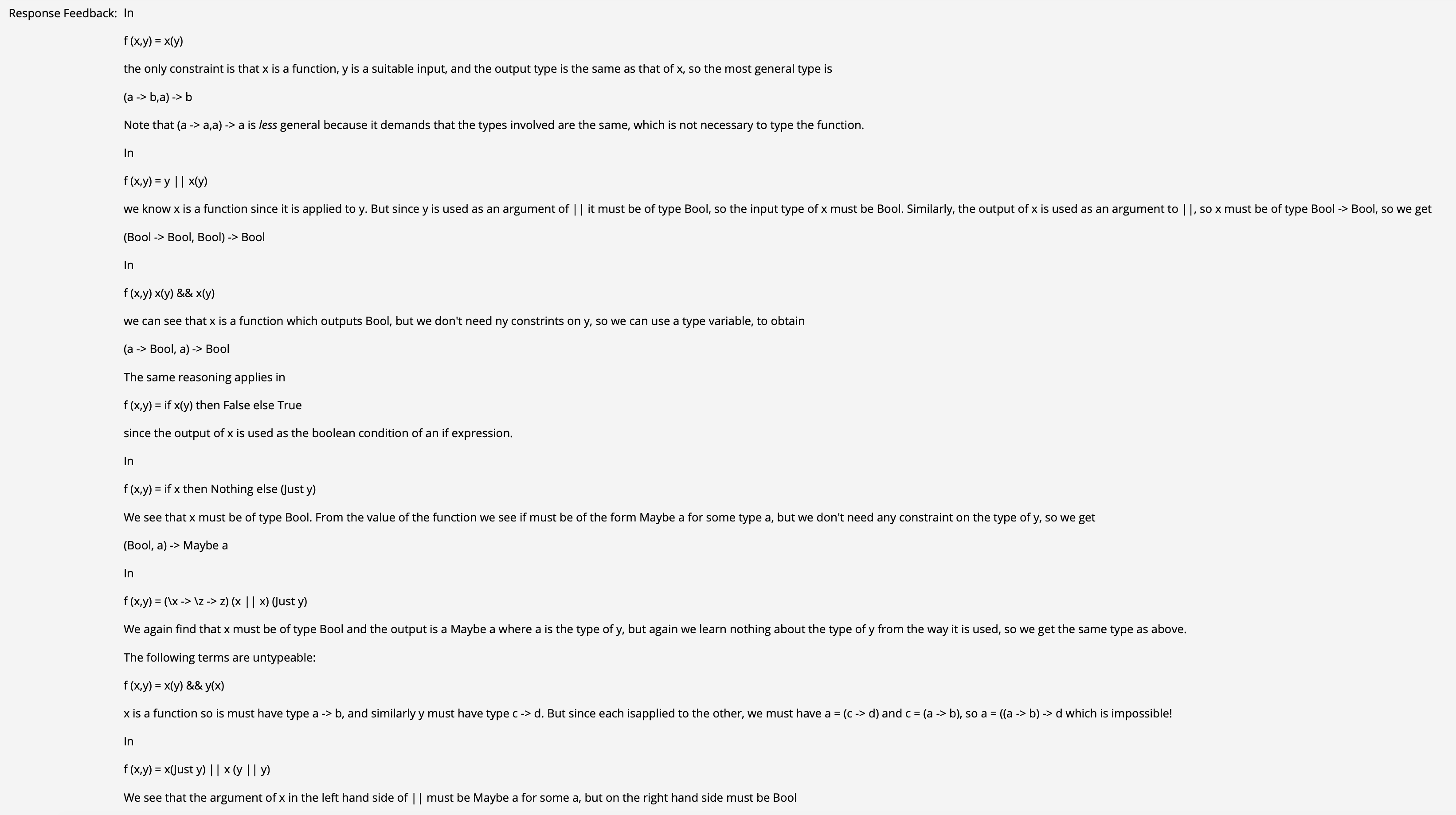
($\uparrow$ 由于取并运算符 || 具有短路特性, 因此如果第一个元素为 $1$ 时它会返回 True, 但如果第一个元素是 error 的话就不一样了)

($\uparrow$ 注意: 对第三个函数而言, 显然它在 base case 中就已经检查了全部两个变量的结构; 对第四个函数而言, 它不但检查了变量的结构, 由于存在 x*y, 乘法中任何变量都不能是 error, 因此它对于输入内部的任何变量也都是严格的. 对于最后两个函数而言, 它的输出不涉及对输入内部元素 y 的检查, 而是 原样输出, 因此函数对输入的内部元素 不是严格的.)
($\uparrow$ 注意 !! 运算符是从列表中取对应位置的元素就可做出这题. 出错是因为 Blackboard 的类型匹配不太灵光…)
4. Haskell: 更多类型
本节我们进一步探讨 Haskell 的类型系统.
参数 (Parametric) 多态和特定 (Ad-Hoc) 多态
参数多态 指声明函数时 不指定 其具体参数的类型, 而 特定多态 允许函数有多个同名但参数类型不同的实现, 在编译时基于传入的参数类型不同而选择相应版本的函数.
首先讨论 Haskell 中的参数多态:

在上图代码的第 $3$ 行中, 我们定义该函数 接受任意类型的数据 作为输入. 而第 $8,8$ 行中定义的函数 g 实际上的参数规定是: “h是一个接受任何数据类型作为输入的函数”.
因此, 第 $9$ 行实际上 ”约束了“ $h$ 的类型为只接受整数和布尔型输入, 而非任何输入. 因此报错. (这实际上就是 “任意给定” 和 “给定任意” 的问题: 我们常规的理解是: 这里的类型 b 是 任意给定的, 而 Haskell 则认为它应该是 给定任意.)
而对于第 $13, 14$ 行: $13$ 行的描述是 “对任何类型a, p都是 (a, a)” 但 $14$ 的定义是 “p是一个 (boolean, bolean)”, 因此也会报错.
然后讨论 Haskell 中的特定多态 (也就是 Overloading):
Haskell 中最显然的特定多态例子就是 数值运算 和 控制台输出. 我们使用类型不同的参数作为输入, 都可以对应地得到正确的结果.
要实现这样的功能, 就需要对函数的不同类型的输入进行对应的实现.
考虑下面的例子:

在该例子中, 我们定义了一个 类型类 (TypeClass): Descriptive, 它 不约束作为输入的类型, 但约束输出类型必须为 String. 在此之下我们 实现了 Descriptive 类的两个实例, 分别是 Bool -> String 和 Int -> String. 注意第 $35$ 行: 由于整数在 Haskell 中有重载, 因此需要手动标注它的类型为 Int 让编译器认出它表示的是整数.
下面考虑 多态 但只接受类型为 Descriptive 的输入的话函数.
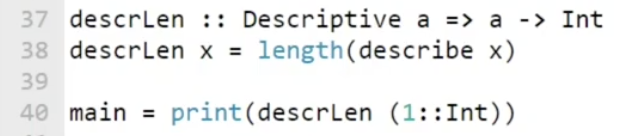
在这个例子中, 我们定义了一个 只接受类型为 Descriptive 的输入的函数, 它返回的是 对应类型的描述字符串的长度. 对输入类型的约束是在 $37$ 行 Descriptive a => a -> Int 实现的. 这一行应该这么理解: 如果 a 是一个 Descriptive 类型, 则该函数接受 a, 输出 Int. 注意双箭头表示 类型约束.
下面再考虑 类型类实例定义中的类型约束: 目标为构造一个对 [descriptive a] (以 Descriptive类型 作为内部元素的列表) 这个数据类型的 Descriptive 类实现, 就需要在类型约束中明确: 我们只接受元素类型也是 Descriptive 的列表.
回顾上面对 descrLen 的定义中我们在 函数的类型定义 里使用了双箭头表示的 类型约束, 在实例化类型类时, 我们也可以在类型类的 类型定义 中使用同样的约束.

此时 $33$ 行读作: “如果元素 a 的类型是 Descriptive, 则该实例接受以 Descriptive 类型为元素的列表 [a], 输出 Int”.
从上面的简单例子我们可以看出, 在 Haskell 中我们是可以通过 将函数的某个输入定义为类型类, 从而 为不同类型的函数输入实现不同的对应函数, 也就是 Ad-Hoc Polymorphism 的.
下面看一个更实际的例子. Haskell 中有一个 内置类型类: Eq, 所包含的是 所有可以通过计算的方式对比是否相等的类型.

上面是一个我们 自行实现 的 Eq 类型类. 注意: 当函数函子是 符号 时, 它会被 Haskell 自动处理为 infix (也就是符号在中间, 参数在两边的那种函数使用形式).
注意此处我们是直接基于 === 的基础上实现 =/= 的. 因此, 对于任何类型, =/= 总是有一个对应的实现 (因为它的实现基于对应类型的 === 的实现), 无论 === 是否已经被实现.
同时, 我们还可以对函数的参数构造更广泛的约束: 我们可以限制函数的某个参数 必须属于某几个数据类型中的其中一个.
考虑下面的例子:

在上面的例子中, 对函数 ifEqD 中参数类型的约束是从 $58$ 行函数的具体实现中 反推出来 的: 观察到 y, z 显然必须是 Descriptive 类型, 而前两个参数由于需要被应用在 === 上, 因此只能是 MyEq 类型. 由此才得到这个函数 最一般 (Most General) 的类型约束: (Descriptive b, Descriptive c, MyEq a) => a -> a -> b -> c -> String.
我们最后介绍一个内置类型类: show. 它 接受任意数据类型作为输入, 并以 String 作为输出类型. 其作用是返回对输入的数据类型的描述.
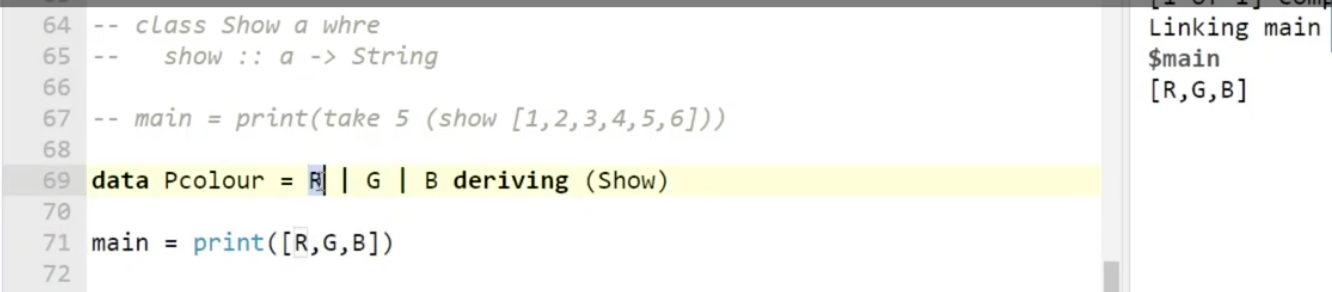
在 Haskell 中, show 有一个默认实现, 但这个默认实现 不会被默认应用在用户自定义数据类型上. 考虑如下图所示的代数数据类型 PColor:

如果直接尝试 print(R) 编译器则会报错, 因为对这个自定义数据类型, show 并没有对应的实现 (即便 show 有一个默认实现, 但这个默认实现除非特殊指定否则不会和这个用户自定义类型相关联), 因此 print() 不知道怎么输出, 所以报错.
我们可以在 $69$ 行后加上 “deriving (Show)” 让类型类 show 对这个数据类型使用它的默认/通用实现. 此时如果再 print, 就会原样输出.
Show 的默认实现之所以不会自动和用户自定义类型相关联, 是因为在正常情况下我们往往需要 自己实现对自定义数据类型的描述. 如下图所示:
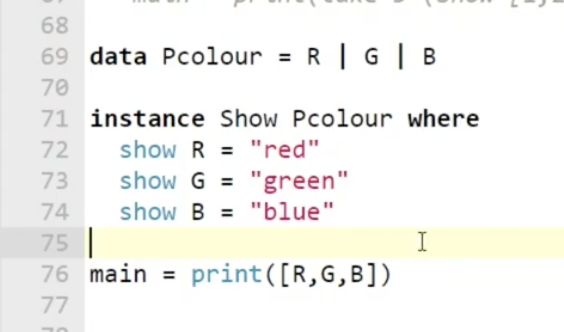
这样我们就 人为地 指定了 show 在应用到这个数据类型上的时候对应的实现应该是什么. 显然对于用户自定义数据类型, 用户肯定比编译器更懂怎么描述它.
相关题目解析:

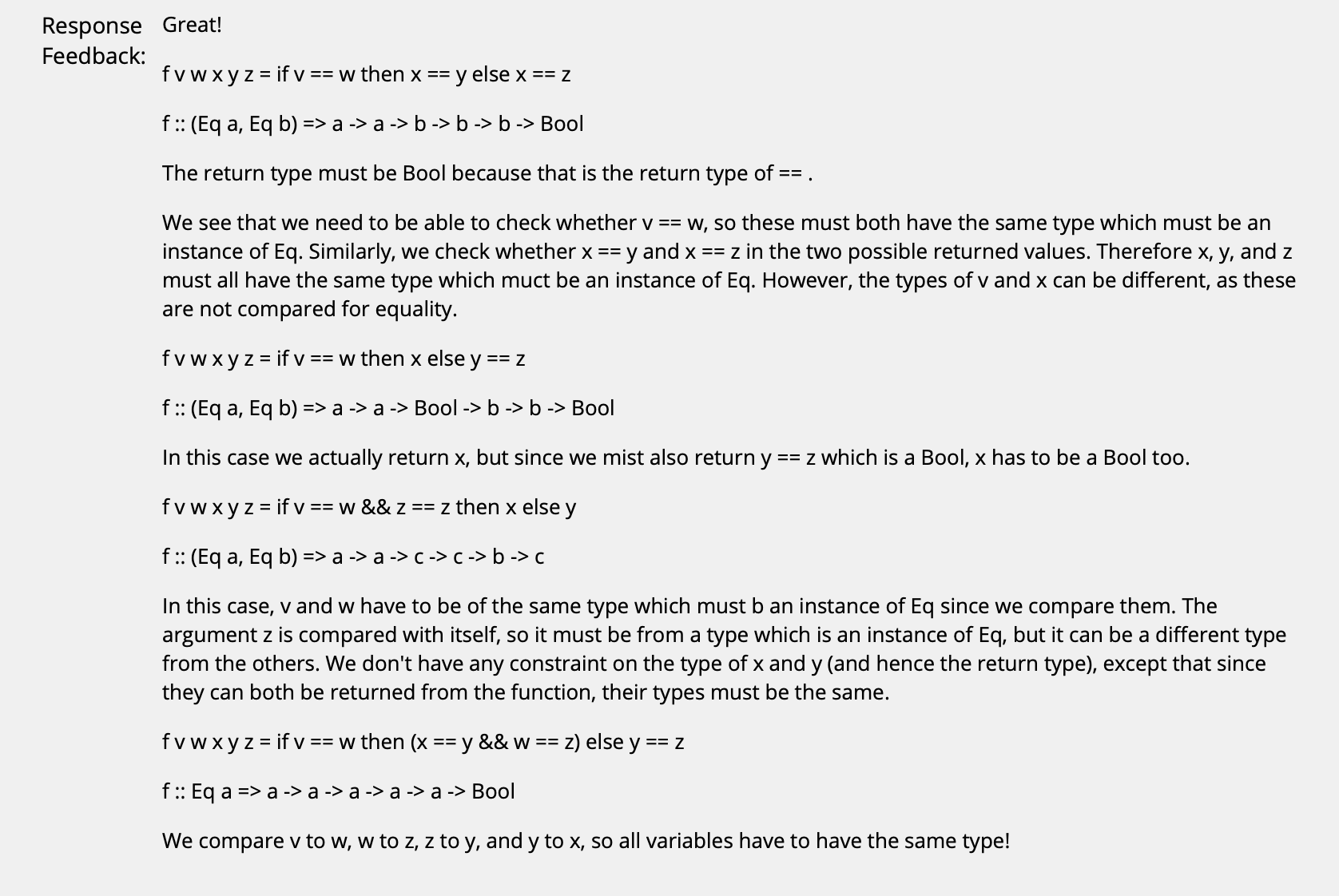
($\uparrow$ 注意, 在涉及到 “==” (也就是 Eq) 时需要注意, 只有等式两边的变量类型相同才能比较是否相等. 如果有 Show 的话需要加上约束: 该变量被 Show 实现了, 也就是 Show x, x是对应变量. 我们还可以根据函数的返回值倒推变量的类型.)

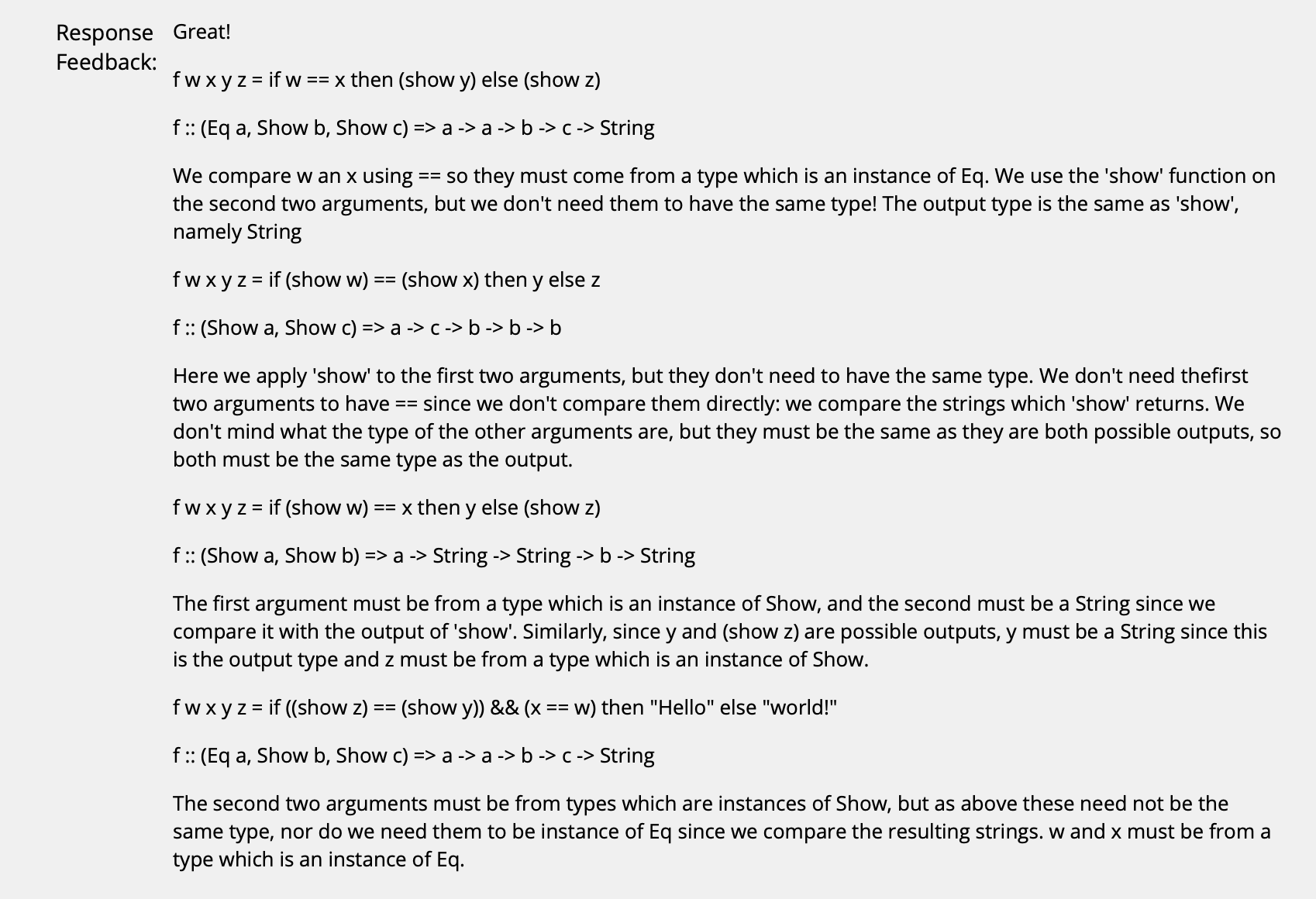
($\uparrow$ 做这种类型的题时需要时刻注意: 一定要尽可能地选择最一般化, most general 的结果.)


($\uparrow$ 前两个是 untypable 的原因是, 它们的输出类型 不固定. 如果出现这种情况是无法赋予类型的! 即便我们指定函数的输出是某个 (b, b), 也不意味着类型 b 就可任意取值看人下菜, 实际情况下它始终有一个固定值!)
5. Haskell: 输入输出
我们在最后一节中讨论如何使用 Haskell 编写 可交互式程序:
回顾我们在本章开头介绍的 Haskell 特征: 万物皆函数 / 万物皆变量. 在 Haskell 中, 输入/输出 也被当成变量处理.
而 Haskell 程序也可被视为一个 定义非常复杂的, 类型为 输入输出 (IO) 的变量. 而无论如何, 在任何 Haskell 程序中我们都 必须定义一个类型为 IO 的常量: main.
而 Haskell 编译器所做的事本质上可以视为: 它基于这个常量 main 的接收值计算它本身的值, 然后生成一个 具备对应输入/输出效果 的可执行文件, 仅此而已.

如上图所示, 第 $1, 2$ 行中的 print 在实际输出时根本不会被 evaluate, 因为输出时所被evaluate的只有第 $4$ 行的东西. 因为只有第 $4$ 行包括了 main. 即使这两行被编译器 evaluate, 其结果也只是: “这两行分别包含了一种 对输出的描述, 而不是输出本身”.
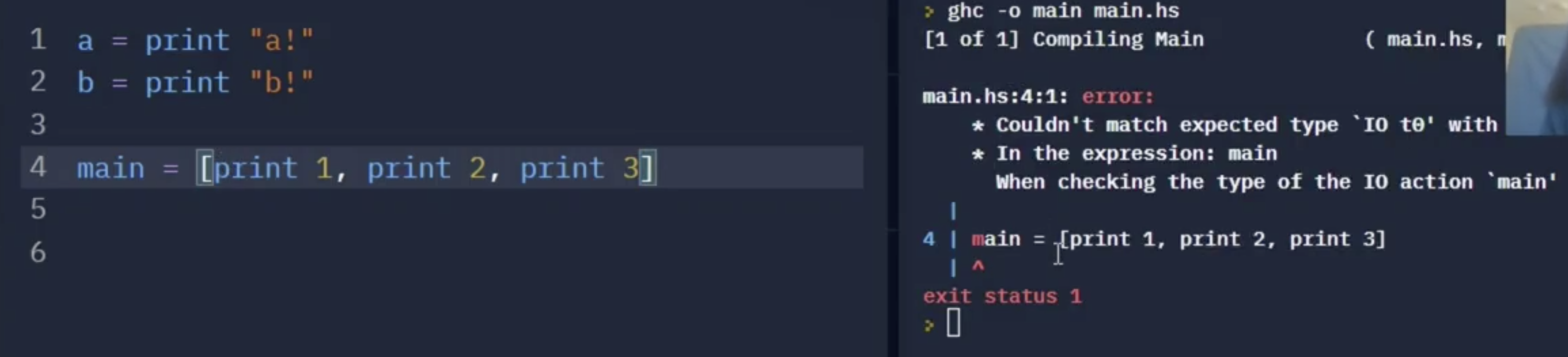
从上面的例子可以看出, main 所接受的只是类型为 IO 的变量. 此时如果我们从列表中取出第一个元素, 则程序可以被正常编译并遵照 print 1 的输出描述, 正常输出 $1$.
此外, 由于 IO Value 只是变量值, 因此它也可以作为 函数的输出:
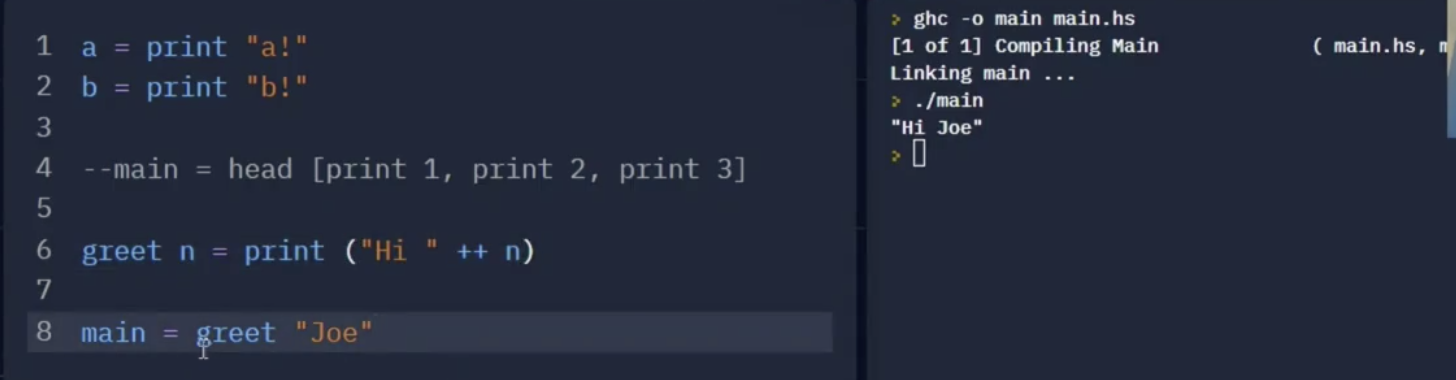
在上面的例子中: greet 只是一个接收字符串作为输入, 返回描述输出行为的, IO 类型变量的一个函数, 它本身不负责任何实际的 IO 操作 (如输出).
除了 print, 我们还可以使用 getLine 描述 Haskell 程序的输入输出行为. getLine 的作用是 从命令行接收用户输入, 并将用户的输入存储在某个变量中供程序的其他部分使用.
而 return 不实际执行任何 I/O 操作, 但 “It make this variable being available to future IO actions that we might carry out”.

下面介绍如何使用 IO Values 中的变量.
I/O behaviour 的输入显然是 无法被确定 的. 因此, 它无法被作为 Haskell 中的常规数学变量, 以函数参数的形式直接参加运算.
但是, 无论 IO 输入的源头是什么 (如用户输入, 网络传入等), 从某一时刻开始只要它被提供, 那么它总是确定的. 因此我们仍然可以 (而且需要!) 对它进行操作.
Haskell 解决这一问题的方法是: 将需要对输入/输出变量进行的操作 (实际上也就是以输入/输出变量作为参数的函数) 嵌入到某个I/O 描述中:
Haskell 提供了一个用于 将 IO 变量 “feed” 到函数中的内置谓词: >>=:
1
>>= :: IO b -> (b -> IO c) -> IO c
它的理解方式为: “>>= 将一个 IO 输入 $b$ 作为函数输入, feed到一个类型为 (b -> IO c) 的函数中, 并将该函数的返回值 IO c 输出.”
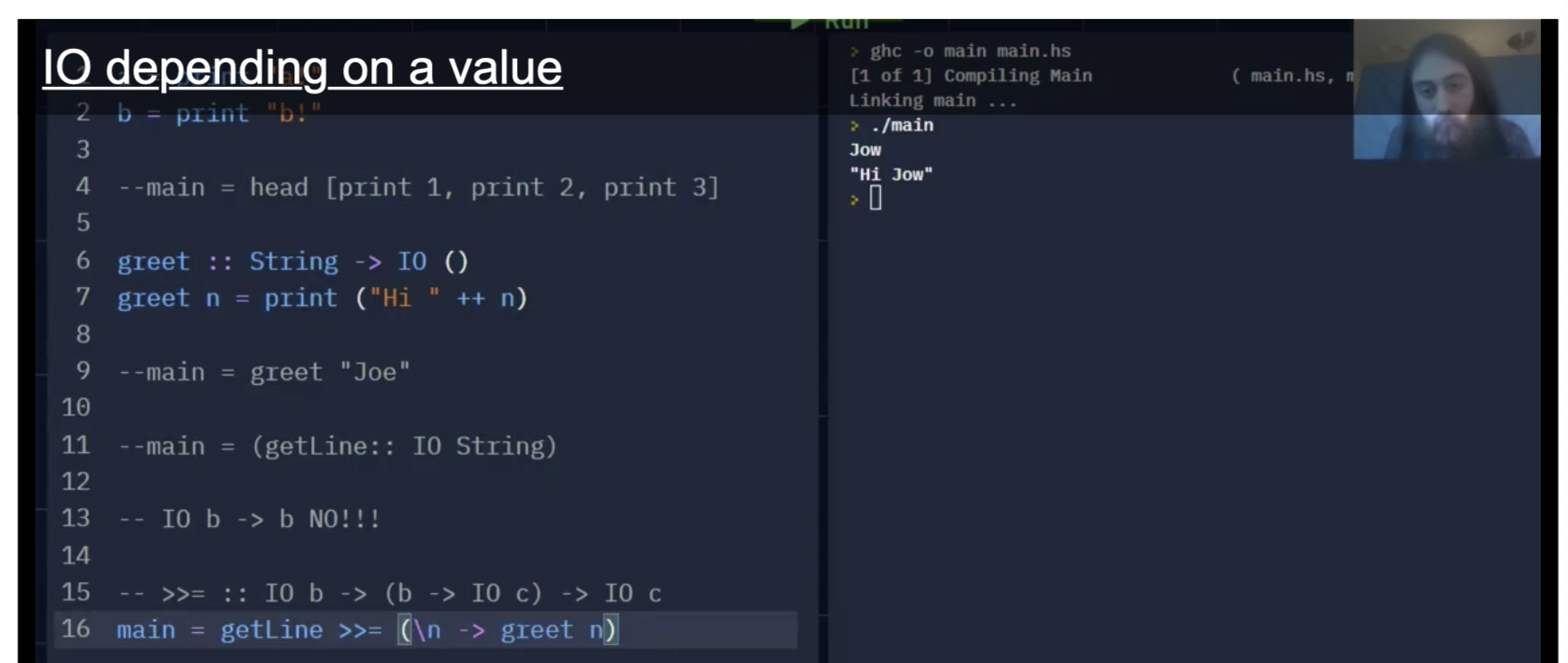
由此可见程序正常执行. 第 $16$ 行的写法只是一种为了方便理解函数传值过程而进行的清晰写法.
同时注意, 如果我们使用 >> 而非 >>=, 则符号左边 IO 操作的输入会被丢弃掉 (Discarded), 不会被作为参数传入右边的函数里.
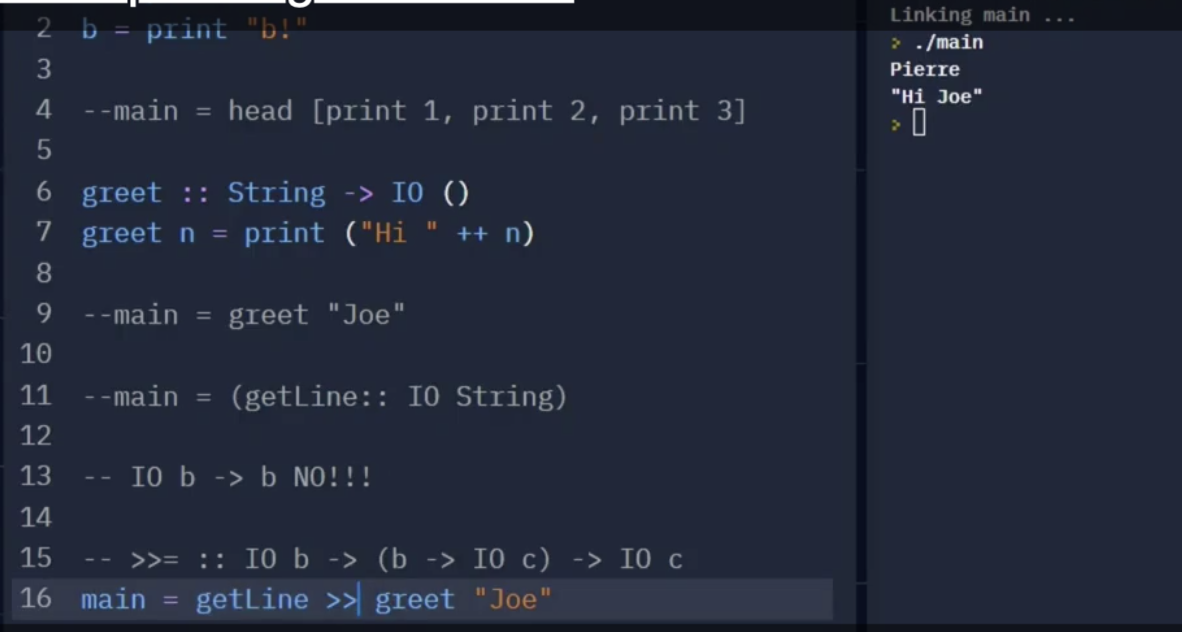
可见, >> 左侧的 IO 输入 “Pierre” 并没有被作为右侧 greet 的输入.
我们最后讨论 递归定义的 IO. 考虑下面的例子:
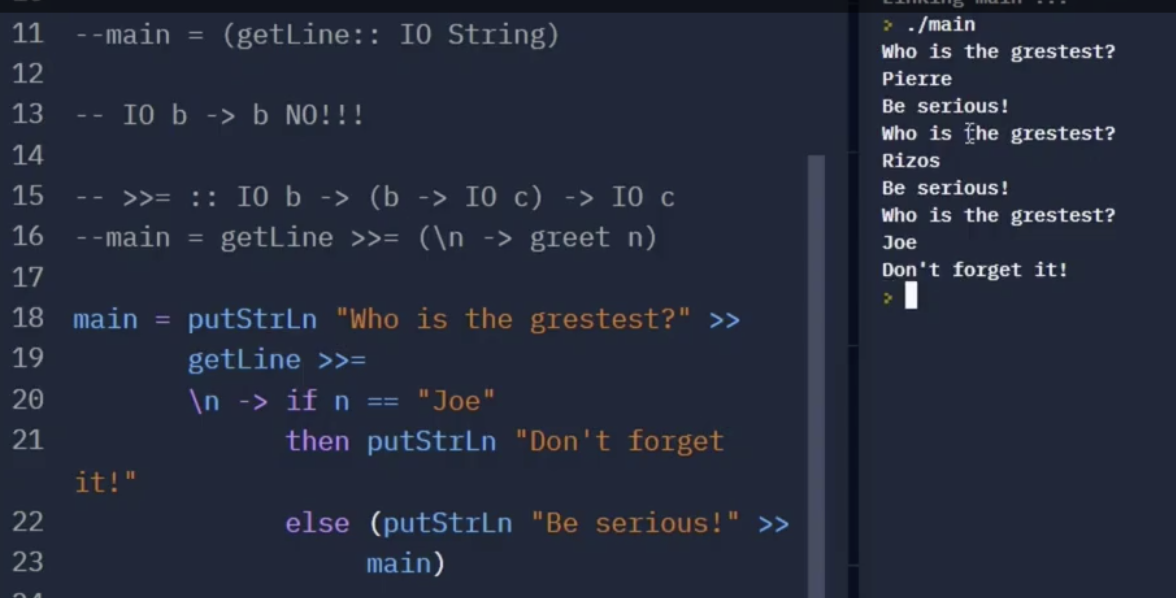
我们可以看到, 上面的函数中定义了这个 IO 对不同输入的返回值. 在 $22, 23$ 行中, 可以看到我们使用了 >> 来 丢弃从 getLine 得到的用户输入, 并 递归调用了 main.
如果我们将 $22$ 行的 putStrLn 替换为 return, 则 “Be Serious” 将不会被输出, 因为 return 不执行任何实际的 IO 操作. 同时由于 return 的作用是保留接受的输入作为变量供后续的 IO 操作利用, 但 main 是一个 不接受任何输入的函数, 所以它在此处毫无作用.
同时需要注意: Haskell 中 不存在控制流语句, return 不会 “让程序从某个循环体中跳出来”, if..else 也不是真正的控制流语句.
在一些特殊情况下, 我们可能需要写很多个 >>= (bind) 算符进行 IO 传值. Haskell 提供了一个语法糖 do 用来 “简化” 写法:

如上图所示, 该函数先后接受两个从控制台传来的用户输入 $n, m$. 这个写法可以被简化为下列的方式:
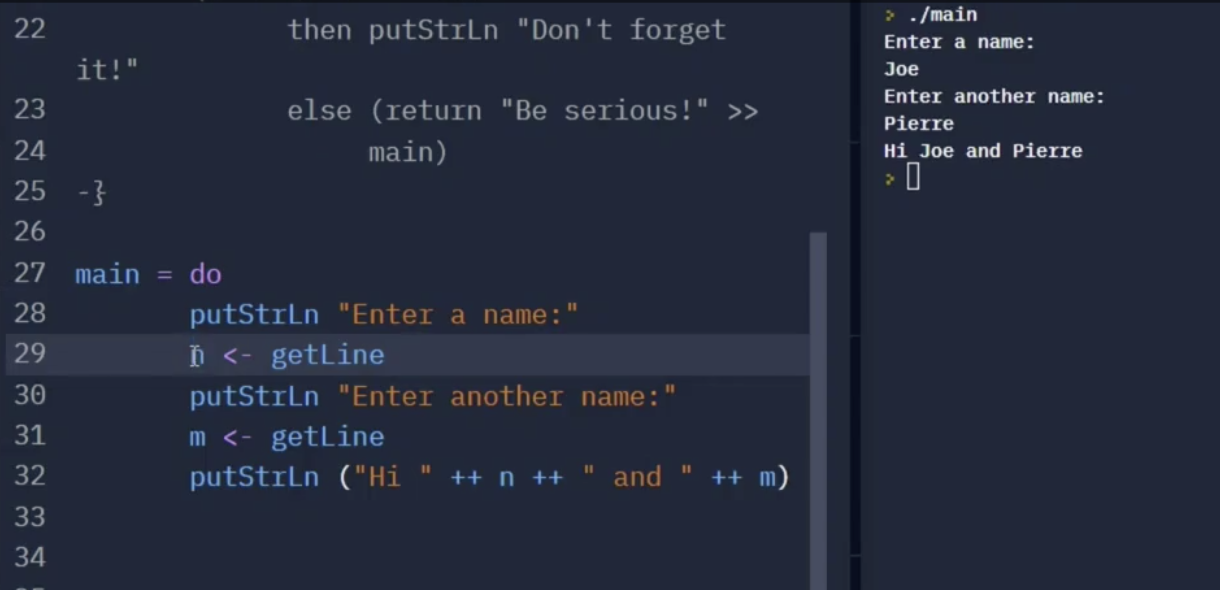
它类似于 “let n = ‘result of getLine’”.
相关题目解析:


($\uparrow$ 注意: 1. “return” 不产生任何实际的 IO 操作, 只是起到类似 “传值” 的作用. 2. 程序实际执行是从最底下 in prog1 那一行开始的.)
