量化布尔公式

在本章中, 我们介绍 量化布尔公式 (Quantified Boolean Formula). 它是基于谓词公式的基础上推广而来的产物, 相比常规的谓词公式多出了 “存在 ( $\exists$)”, “任意 ($\forall$)” 等量化谓词, 因此相比普通的谓词公式, 我们可以使用它更简明地表达相同的问题. 一般而言, 量化布尔公式常被用于表示状态有限的组合问题, 如规划问题或博弈问题.

我们将首先介绍量化布尔公式的语法和语义, 并解释 界限变量 和 自由变量 的定义和性质. 其次, 我们将讨论量化布尔公式的可满足性定义. 在此之后, 我们还将给出量化布尔公式的单调替换定理和等价替换定理, 最后我们研究量化布尔公式的代换 (Substitution).

我们随后给出量化布尔公式可成为的两种 范式 (Normal Form): 前束范式 (Prenex Form) 与 合取范式 (CNF).

最后, 我们将介绍一系列检测量化布尔公式可满足性的方法.

9.1 量化布尔公式

我们首先在本节中介绍量化布尔公式的语法, 语义和它 真假性, 可满足性 的定义, 进而说明对量化布尔公式而言, 检查它的某个解释的真值与检验该公式的可满足性或重言性同等困难的特征. 最后, 我们讨论量化布尔公式中的 界限变量 和 自由变量, 并由这两种新变量类型导致的, 无法在量化布尔公式上使用原本在常规谓词公式上可用的 “代换” 方法的问题, 引入对量化布尔公式的等价性和代换方法的讨论.

9.1.1 语法和语义

从本节开始我们将 布尔变量 简称为 变量. 量化布尔公式相比常规为此公式的推广是通过允许对公式中的变量使用量化谓词修饰而实现的.

定义 9.1.1 (量化布尔公式)

对量化布尔公式的定义相比谓词公式的定义, 只多出了下面的一条:
考虑布尔变量 $p$ 和布尔公式 $F$, 则 $\forall p F$ 和 $\exists p F$ 也都是量化布尔公式.

分别称 $\forall$ 和 $\exists$ 为 全称量词 和 存在量词.

我们同时对量词表达式 $\forall p$, $\exists p$ 给出定义:

1. 若公式 $F$ 中包含 $\forall p$, 则称在 $F$ 中, $p$ 为 全称量化 (Universally Quantified) 的.

2. 若公式 $F$ 中包含 $\exists p$, 则称在 $F$ 中, $p$ 为 存在量化 (Existentially Quantified) 的.

显然地, $\forall p F$ 和 $\exists p F$ 分别表示:

1. 对 $p$ 的任意可能取值, $F$ 的解释均为真.
2. 对 $p$ 的某一个可能取值, $F$ 的解释为真.

下面讨论量化布尔公式的 语义.

我们首先引入一个新的表述:

记 $I, p, b$ 分别为某个 解释, 某个 变量 和某个 布尔值. 则定义 $I[p \leftarrow b]$ 如下:

显然对 $I[p \leftarrow b]$ 而言, 该解释由 $I$ 扩充而来, 它对其他任何不同于 $p$ 的变量的定义均与 $I$ 一致.

我们下面使用上面所定义的这个记号表述量化布尔公式的 真性 (Truth):

定义 9.1.2 (量化布尔公式的真性)

量化布尔公式的真性除了包含 谓词公式的真性的定义 外, 还包括下列两条:

1. $I(\forall p F) = 1$ 当且仅当 $I[p \Leftarrow 0] (F)=1$ 且 $I[p \Leftarrow 1] (F)=1$.
2. $I(\exists p F) = 1$ 当且仅当 $I[p \Leftarrow 0] (F)=1$ 或 $I[p \Leftarrow 1] (F)=1$.

和谓词公式的情形一样, 若 $F$ 在解释 $I$ 下的语义为真, 则记为 $I \vDash F$.

定义 9.1.3~9.1.5 (量化布尔公式的可满足性, 重言性, 等价性)

量化布尔公式的可满足性, 重言性和等价性与常规的谓词公式的定义一致.

需要注意的是, 对某个量化布尔公式而言, 给定它的某个解释进而检查该解释下给定量化布尔公式的值这一操作的复杂性和检验该布尔公式的可满足性等价.

这是因为一旦量化布尔公式中的任何变量被量化谓词修饰 (限定), 我们就需要根据修饰它的量化谓词的不同而相应地考虑不同的情况. 若变量被全称量词修饰, 我们必须考虑公式在该变量取得可取的每一个值的情况下对应的解释; 而若变量被存在量词修饰, 我们则要确保至少在该变量取到某一个值的情况下公式为真, 这也被称为 构造 AND-OR 选择树.

9.1.2 界限变量和自由变量

我们知道, 对谓词公式 $F$, 它的真值取决于 $F$ 中出现的所有变量 $p$ 的值. 而从上述的例子中可以看出, 对量化布尔公式 $G$ 而言, $G$ 在解释 $I$ 下的真值不完全取决于 $I$: $G$ 中任何被量词修饰的变量都会 独立于解释 $I$ 对 $G$ 的真值产生影响, 这一影响不会随着 $I$ 对这些被修饰变量的值的限定而产生改变, 也就是说 $I$ 对这些被修饰变量的值的限定本质上是无效的.

定义 9.1.6 (界限变量和自由变量)

对量化布尔公式 $F$ 而言, 若在它中所出现的某个变量 $p$ 被全称量词或存在量词中的任意一个所修饰, 则称其为 界限变量. 若 $p$ 在公式中没有被任何一种量词修饰, 则称其为 自由变量.

我们接下来对量化布尔公式的 子式, 极性, 量化布尔公式中变量的 自由出现 和 受限出现 给出定义:

定义 9.1.7 (量化布尔公式的子式)

对量化布尔公式的子式的定义相比谓词公式中的定义扩展了下列一条:
公式 $F_1$ 是 $\forall p F_1$ 和 $\exists p F_1$ 的子式.

定义 9.1.8 (量化布尔公式的极性)

对量化布尔公式的极性的定义相比谓词公式中的定义扩展了下列一条:
记 $F\vert _{\pi} = G$, 且 $G$ 形为 $\forall p G_1$ 或 $\exists p G_1$. 则 $\pi . 1$ 为 $F$ 中的一个 位置, 且 $F \vert _{\pi.1} \overset{def}{=} G_1$ 且 $\text{pol}(F, \pi.1) \overset{def}{=} \text{pol}(F, \pi).$

注: 在量化布尔公式中, 我们沿用 “谓词公式的极性” 定义中, “正出现” 与 “负出现” 的定义.

定义 9.1.9 (量化布尔公式中变量的自由出现与受限出现)

考虑布尔变量 $p$, 且 $F\vert _{\pi} = p$ (即 $p$ 在量化布尔公式 $F$ 中), 称 “$p$ 在量化布尔公式 $F$ 的位置 $\pi$ 上的一次出现” 为 受限出现, 若这次出现所在的位置 $\pi$ 可表示为两个子位置 $\pi_1, \pi_2$ 的联结, 且 $F\vert _{\pi_1}$ 形如 $\forall p G$ 或 $\exists p G$, 反之称这次出现为 自由出现.

上述的形式化定义用人话表示, 就是说, 若变量 $p$ 在 $F$ 的某个位置上被某种量化谓词修饰, 则称 $p$ 的这次出现为 受限出现, 反之这次出现则为 自由出现.

定义 9.1.10 (自由变量与受限变量)

这个定义是 定义 9.1.9 的推广. 若 $F$ 中的某个变量 $p$ 在其中有至少一次受限出现 (或自由出现) , 称其为 $F$ 的受限变量 (或自由变量).

需要注意的是, 量化布尔公式中的一个变量可以 既是自由变量, 同时也是受限变量, 如

中, 变量 $p$ 的第一次出现是自由的, 而最后一次出现就是受限的. 同时, $q$ 在该公式中只有受限出现, $r$ 只有自由出现.

我们最后引入一个记号. 从此开始, 我们使用记号 $\exists\forall$ 表示 “任一种量词”.

定义 9.1.11 (闭的量化布尔公式)

称量化布尔公式为 闭 的, 若该公式中不存在任何自由变量.

9.1.3 真性和满足性

我们下面讨论如何检验量化布尔公式的真性和可满足性.

首先基于第一小节中对量化布尔公式真性的定义, 我们不难得出下列结论: 量化布尔公式的真值只取决于它自由变量的值.

引理 9.1.1

记 $I_1, I_2$ 为对量化布尔公式 $F$ 上所有自由变量具有相同定义的两个解释, 则 $I_1 \vDash F$ 当且仅当 $I_2 \vDash F$.

由上述结论, 我们可得到这个结果:

引理 9.1.2

对 闭的量化布尔公式 而言, 它的 真性, 重言性, 可满足性 等价:
对任意解释 $I$ 和闭的量化布尔公式 $F$, 下列三个命题等价:

1. $I \vDash F$.
2. $F$ 是可满足的.
3. $F$ 是重言式.

证明
首先可知, $F$ 为重言式 $\Rightarrow I \vDash F \Rightarrow F$ 为可满足的.

其次可知, 若 $F$ 为可满足的, 则存在某个解释 $I_1$ 满足 $I_1 \vDash F$. 由 引理 9.1.1, 知任何与 $I_1$ 对于 $F$ 的自由变量具有相同定义的解释 $I_2$ 同样满足 $I_2 \vDash F$. 由于 $F$ 不存在自由变量, 因此对任意 $I_2$, 均满足 $I_2 \vDash F$. 因此 $F$ 为重言式. $\blacksquare$

一般地, 我们可将量化布尔公式的可满足性和真性视为 闭的量化布尔公式的可满足性 (或真性/重言性) 的特殊情况.

引理 9.1.3

记 $F$ 为量化布尔公式, 其自由变量为 $p_1, p_2, \cdots, p_n$, 则 $F$ 为可满足的 (或重言的), 当且仅当 闭的量化布尔公式 $\exists p_1, \exists p_2, \cdots, \exists p_n F$ (或 $\forall p_1, \forall p_2, \cdots, \forall p_n F$) 为可满足的.

9.1.4 等价性: 单调替换定理和等价替换定理

我们下面考虑定义在量化布尔公式中定义谓词公式所具备的单调替换定理和等价替换定理.

定理 9.1.1 (量化布尔公式的单调替换定理)

记 $F_1$ 为量化布尔公式 $G_1$ 的子式, 且 $F_1 \rightarrow F_2$ 为重言式. 将 $G_1$ 中 至少一处$F_1$ 的正出现 (或负出现) 用 $F_2$ 替代, 则公式 $G_1 \rightarrow G_2$ (或 $G_2 \rightarrow G_1$) 也是重言的.

换言之, 量化布尔公式的真值在正出现的子公式上是单调的, 在负出现的子公式上是反单调的.

我们进而有下述的等价替换定理:

定理 9.1.2 (量化布尔公式的等价替换定理)

记 $F_1$ 为量化布尔公式 $G_1$ 的子公式, 且 $F_1 \equiv F_2$. 记 $G_2$ 为从 $G_1$ 中替换至少一处 $F_1$ 出现为 $F_2$ 得到的公式, 则 $G_1 \equiv G_2$.

9.1.5 代换

值得注意的是, 由于受限变量的存在, 常规谓词公式的等价替换定理不适用于量化布尔公式. 考虑解释 $I = {p \rightarrow 1, ~ q \rightarrow 1}$, 则有 $I \vDash q \rightarrow p$. 由于 $I \vDash \forall \exists p (q)$和 $\neg I \vDash \forall \exists p (p)$, 显然 $I \vDash p \leftrightarrow q$ 成立, 而 $I \nvDash \forall p (p) \leftrightarrow \forall p (q)$.

由于在本章将要介绍的一系列公式中都将涉及到对任意公式 (包括量化布尔公式的子公式) 的替换, 我们将在本节中讨论受限公式的替换问题.

定义 9.1.12 (对某个变量自由的公式)

记量化布尔公式 $F, G$, 记 $p$ 为变量. 称 $G$ 对于 $F$ 中的 $p$ 自由, 若将 $F$ 中变量 $p$ 的全部出现用 $G$ 替换后, 对 $G$ 中任何一个自由变量而言, 它都不会在替换后, 成为 $F$ 中的一个受限变量, 换言之 $G$ 中不能出现在原先的 $F$ 中被量词限定的变量. 用更正式的语言表述: 称 $G$ 对于 $F$ 中的变量 $p$ 不是自由的, 若存在路径 $\pi_1, \pi_2$ 和 公式 $F_1$, 使 $F_{\pi_1. \pi_2} = p$, 且 $p$ 在位置 $\pi_1. \pi_2$ 上的出现是自由的, 且 $F_{\pi_1} = \exists \forall q F_1$, 其中 $q$ 为 $G$ 中的某个自由变量.

显然, 在公式 $F := \exists q(\neg p \leftrightarrow q)$ 中, 公式 $q$ 关于 $F$ 中的变量 $p$ 就不是自由的. 一般地, 公式 $G$ 对于 $F$ 中的变量 $p$ 是自由的, 当且仅当变量 $q$ 不为 $G$ 中的自由变量.

若 $F, G$ 均为量化布尔公式且 $p$ 为变量, 我们记 通过将公式 $F$ 中, 变量 $p$ 的所有自由出现替换为公式 $G$ 所得到的公式 为 $F_{p}^{G}$. 注意, 使用这一记号等同于默认 $G$ 关于 $F$ 中的变量 $p$ 为自由的.

若我们需要将 $F$ 中的某个变量 $q$ 替换为公式 $G$, 而公式 $G$ 并不关于 $F$ 中的变量 $q$ 自由, 我们就需要 先将 $F$ 转换为公式 $F’$, 使得 $G$ 关于 $F’$ 中的变量 $q$ 自由, 然后再执行替换. 转换的实质是将 $F$ 中的某个 (或某些) 受限的, 但在 $G$ 中是自由的变量替换为其他的受限变量, 这一操作被称为 受限变量重命名. 下面我们给出一个它的, 适用于大多数情况的定义.

定义 9.1.13 (受限变量重命名)

称公式 $F’$ 是通过将公式 $F$ 中的受限变量重命名而得到的, 若 $F’$ 可通过一系列步骤从 $F$ 转换而来:
设 $\exists \forall p G$ 为 $F$ 的某个子公式, $q$ 为某个 未在 $F$ 中出现过的变量, 将 $\forall \exists p G$ 替换为 $\forall \exists q (G_{p}^{q})$.

引理 9.1.4

若 $F’$ 为通过重命名受限变量从 $F$ 转换而来的公式, 则 $F’ \equiv F$.

定义 9.1.14 (经修正的公式)

称 $F$ 为 经过修正的, 若它满足下列几条约束:

1. $F$ 中 不存在既受限又自由 的变量.
2. 对任意变量 $p$, $F$ 最多包涵一个限定它的量词.

举例而言, 公式 $\exists p \neg p \rightarrow \exists \neg p$ 因包含两个限定 $p$ 的量词 $\exists$ 而不是修正的, $\exists \neg p \rightarrow p$ 同样不是修正的, 因其中 $p$ 既是受限的, 也是自由的. 但显然, 这两个不同的量化布尔公式都可以通过对受限变量重命名而得到修正. 因此, 我们进一步地可以得到下列结果:

引理 9.1.5

任何量化布尔公式都可通过对受限变量重命名转化为一个语义上等价的, 经修正的公式.

9.2 范式

在本节中我们考虑量化布尔公式的两种范式. 在对谓词公式的学习中, 我们引入了合取范式和子句范式, 而我们即将讨论的两种范式为前束范式与合取范式.

9.2.1 前束范式

粗略地说, 所有满足 “限定公式中任何受限变量的量词都位于公式开头” 的量化布尔公式都属于前束范式.

定义 9.2.1 (前束范式)

称量化布尔公式 $F$ 为 前束范式 或 前束公式, 若它形为

$$\exists \forall_{1}p_1 \exists \forall_2 p_2 \cdots \exists \forall_{n} p_n G$$

其中 $G$ 为不含任何量词的谓词公式.称公式 $F$ 为 $G$ 的前束范式, 若 $F$ 是前束的且 $F \equiv G$.

算法 9.2.1 (量化布尔公式前束范式转换算法)

通过不断使用下列的重写规则将 经过修正的公式 $F$ 进行转换, 当我们再也无法对其应用重写规则时所得到的公式则为 $F$ 的前束范式.

引理 9.2.1

上述的全部重写规则在应用到经修正的公式上时都保持其语义.

值得注意的是, 我们对经修正的公式应用上述任一条重写规则所得到的新公式仍是经过修正的. 此外, 需要注意到, 前束化算法的重写规则不适用于双蕴含 $\leftrightarrow$, 双蕴含必须在执行前束化算法前被等价替换掉.

定理 9.2.1

记 $F$ 为不包含双蕴含谓词的, 经修正的量化布尔公式. 则将它作为前束化算法的输入时, 算法的输出为 $F$ 的前束范式.

证明
由于可终结性显然恒成立, 且由 引理 9.2.1 可知在每一步转换中算法都保持语义, 因此上述定理显然成立. $\blacksquare$

9.2.2 合取范式

下面我们研究量化布尔公式的合取范式.

定义 9.2.2 (量化布尔公式的合取范式)

称量化布尔公式 $F$ 为 合取范式 (CNF), 若它为下列三种形式的任一种:

1. $\perp$
   
2. $\top$
   
3. $\exists \forall_{1}p_1 \exists \forall_2 p_2 \cdots \exists \forall_{n} p_n F_1$
   其中 $n \geqslant 0$ 且 $F_1$ 为某个为合取范式的谓词公式.
   

称公式 $G$ 为 $F$ 的合取范式, 若 $G \equiv F$ 且 $G$ 为合取范式.

换言之, 量化布尔公式 $G$ 为合取范式, 若 $G$ 为前束范式且它的谓词公式部分是 (谓词公式的) 合取范式.

结合谓词公式的合取范式转换算法与量化布尔公式的前束范式转换算法, 我们就可以构造出量化布尔公式的合取范式转换算法. 需要注意的是, 这一算法沿袭了前束范式转换算法的 全部限制.

算法 9,2.2 (量化布尔公式的合取范式转换算法)

量化布尔公式的合取范式转换算法的重写规则是谓词公式的合取范式转换算法的重写规则与量化布尔公式的前束范式转换算法的重写规则相结合的产物.
在执行合取范式转换算法时, 若在任一步上得到的公式不是经过修正的, 我们需要应用受限变量重命名规则将修正后才能继续应用重写规则.

定理 9.1.3

量化布尔公式的合取范式转换算法具备可终止性, 且它的输出必为输入公式的合取范式.

9.3 可满足性检测: 分割算法和DPLL算法

我们将在最后一节中讨论量化布尔公式的可满足性检测问题.

在展开讨论之前, 我们首先约定对量化布尔公式的简化规则与其 “真假” 的定义:

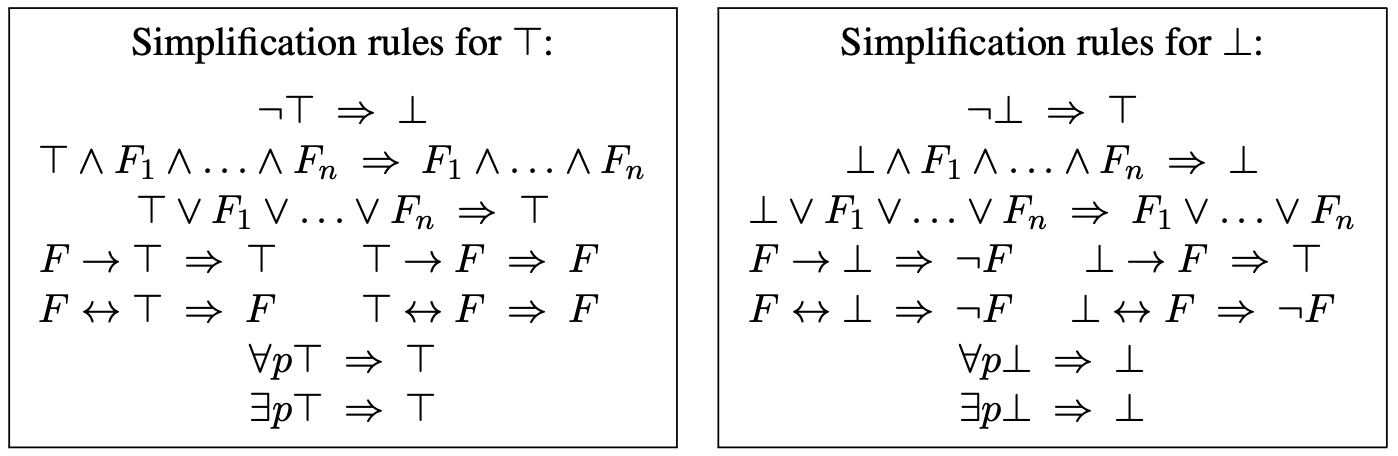
引理 9.3.1

1. 称闭的量化布尔公式 $\forall p F$ 为真, 当且仅当 $F_{p}^{\perp}$ 和 $F_{p}^{\top}$ 均为真.
   
2. 称闭的量化布尔公式 $\exists p F$ 为真, 当且仅当 $F_{p}^{\perp}$ 和 $F_{p}^{\top}$ 至少一个为真.
   

谓词公式的分割算法基于这个简单的原则: 将公式划分为 $F_{p}^{\perp}$ 和 $F_{p}^{\top}$, 并对包含 $\perp$ 或 $\top$ 的公式进行简化. 对量化布尔公式而言, 我们自然需要扩充简化规则, 将对量词的简化也包括进来.

我们进一步引入一个简单的记法. 考虑量化布尔公式 (前束范式)

其中 $G$ 为谓词公式. 称 $F$ 最外层的前缀 为 $\exists \forall_1 p_1 \cdots \exists \forall_i p_i$, 其中 $\exists \forall_1 = \cdots = \exists \forall_i$.

举例而言, $\exists p \exists q (p \wedge q)$ 的最外层前缀为 $\exists p \exists q$, 而 $\forall p_1 \exists p_2 \exists p_3 G’$ 的则为 $\forall p_1$.

算法 9.3.1 (量化布尔公式的分割算法)

量化布尔公式的分割算法如下图所示.

引理 9.3.2 (纯原子)

记 $p$ 为布尔变量, $F$ 为量化布尔公式:

1. 若 $F$ 的所有出现均为正, 则 $\exists p F$ 和 $F_{p}^{\top}$ 等价, 且 $\forall p F$ 和 $F_{p}^{\perp}$ 等价.
   
2. 若 $F$ 的所有出现均为负, 则 $\exists p F$ 和 $F_{p}^{\perp}$ 等价, 且 $\forall p F$ 和 $F_{p}^{\top}$ 等价.
   

我们最后对量化布尔公式的 DLL 算法进行讨论. 它在谓词公式情况下的相应形式是结合单位传播法与合取范式得到的. 由于全称量词的存在, 我们不能直接在量化布尔公式上沿用谓词公式的单位传播法: 一个显然的例子是, 考虑公式 $\forall p (p)$, 它本身显然是不可满足的, 但若对它应用单位传播法, 得到的结果是可满足的 ${p}$.

因此, 在量化布尔公式的单位传播法中, 我们认定任何形如 $\forall p (p \wedge F)$ 为不可满足的, 而 $\exists p (p \wedge F)$ 则与 $F_{p}^{\top}$ 等价.

定义 9.2.3 (单位传播)

记 $S$ 为由一系列子句组成的集合, $Q$ 为一系列量词 $\exists \forall_1 p_1 \cdots \exists \forall_n p_n$. 称这一系列子句组成的集合 $S‘$ 是结合量词序列 $Q$, 通过 单位传播 从 $S$ 得来的, 若 $S’$ 为从 $S$ 使用一系列转换所得来:
若 $S$ 包含一个由单个文字 $L$ 组成, 形如 $p$ 或 $\neg p$ 的单位字句 (Unit Clause), 则

1. 若 $Q$ 包含 $\forall p$, 则将 $S$ 替换为集合 ${\square}$.
2. 否则进行下列操作:
   2.1 将 $S$ 中所有形如 $L \vee C’$ 的子句移除.
   2.2 将 $S$ 中所有形如 $\widetilde{L} \vee C’$ 的子句取代为 $C’$.
   

算法 9.3.2 (量化布尔公式的 DLL 算法)

量化布尔公式的 DLL 算法如下图所示:

其中, select_literal() 每次从公式中选出一个被量词修饰的谓词变量.

我们同样可以引入纯文字法则 (Pure Literal Rule). 考虑量词前缀 $Q$, 引入关于量词前缀的偏序 $>_{Q}$: 若在 $Q$ 中, $p$ 先于 $q$ 出现, 则记 $p > q$, 如在 $Q = \forall p \exists q \forall R$ 中, 就有 $p > q > r$.

进一步地, 我们可以将这样的顺序推广到文字上. 对于分别包含变量 $p_1, p_2$ 的文字 $L_1, L_2$, 若 $p_1 > p_2$, 则 $L_1 > L_2$.

下面约定一个记法: 称文字 $L$ 在 $Q$ 中为 全称 (存在) 的, 若 $Q$ 包含 $\forall p$ ($\exists p$) 且 $p$ 在 $L$ 中出现.

下面看一个例子: 考虑 (显然为合取范式) 公式

该公式的量词前缀 $Q := \exists p \forall q \exists r$, 且$p > q > r$.

同时由 $p > q$ 可知 $p > \neg q, ~ \neg p > \neg q, ~ \neg p > q$.

在该公式中, 全称文字分别为 $p, \neg p, r, \neg r$, 而存在文字为 $q, \neg q$.

引理 9.3.3 (全称文字删除规则)

令 $G = Q(C_1 \wedge \cdots \wedge C_n)$ 为一个闭合的, 修正的合取范式, 其中 $Q$ 为量词前缀. 假设某个 $C_i$ 不为重言式, 且它包含一个在 $Q$ 内全称 (Universal) 的文字 $L$. 若该文字在关于谓词变量的偏序 $>$ 下比 $C_i$ 中任何存在文字都小, 则从 $C_i$ 中删除 $L$ 不影响 $G$ 的真值.

举例而言, 考虑 $Q = \forall q \exists q \forall r \exists s$, 则从 $Q$ 中任何不为重言式的字句中删除任何包含 $r$ 但不包含 $s$ 的文字都不会改变 $Q$ 的真值.

进一步地我们可以立即得到下列的结论:

若某个子句 $C_i$ 只包含在 $Q$ 中全称的文字, 则 $G$ 是不可接受的, 因为更具上述引理, 我们可以将 $C_i$ 简化为空子句.

• Previous
  逻辑学探幽 Part8
• Next
  逻辑学探幽 Part10