二元决策图
在本章中, 我们将介绍一种可以高效表示含有逻辑连接词的, 复杂谓词公式的数据结构: 二元决策图 (BDD). 该数据结构具有以下的三个基本特征:
- 能够简洁地表示谓词公式, 或由谓词公式所表示的布尔函数.
- 可以执行对谓词公式的逻辑运算 (布尔运算).
- 能够被用于检查谓词公式的基本性质, 如可满足性和等价性.
下面我们首先通过引入二元决策树并, 进而对和它相似的数据结构: BDD (Binary Decision Diagram) 进行介绍, 并阐明它的基本特点和性质. 随后, 我们进一步对 BDD 进行推广, 阐明另一种数据结构: OBDD (Ordered Binary Decision Diagram, 有序二元决策图) 的定义和性质.
8.1 二元决策树
回顾在 第四章 中所介绍的分割算法 Splitting Algorithm, 通过对谓词公式应用分割算法, 我们可以得到一棵 分割树. 如下例所示, 对谓词公式
应用分割算法, 所得到的分割树如下图所示:
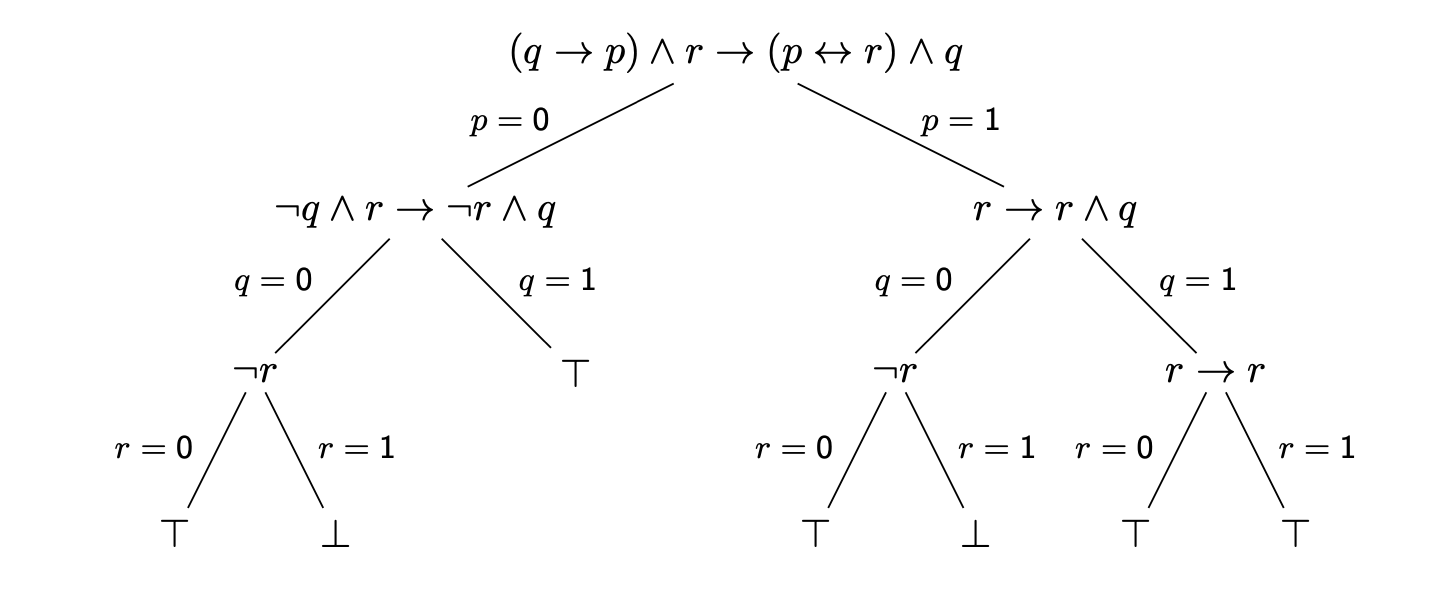
通过将分割树中的叶子节点 $\top$ 和 $\perp$ 替换为 $1$ 和 $0$, 将树的内部节点从原本的谓词公式替换为在该节点处将要被赋值的谓词变量, 再将分割树的边替换为从上一级节点指向下一级节点的箭头, 将标记直接替换为对应的赋值, 分割树就被转换为了二元决策树的形式. 在本章中, 我们使用另一种二元决策树的表示法, 其形式如下图右侧所示.
注意, 在我们的表示方式中, 代表赋值 $0$ 的虚线边始终连接左侧节点, 代表赋值 $1$ 的实线始终连接右侧节点.
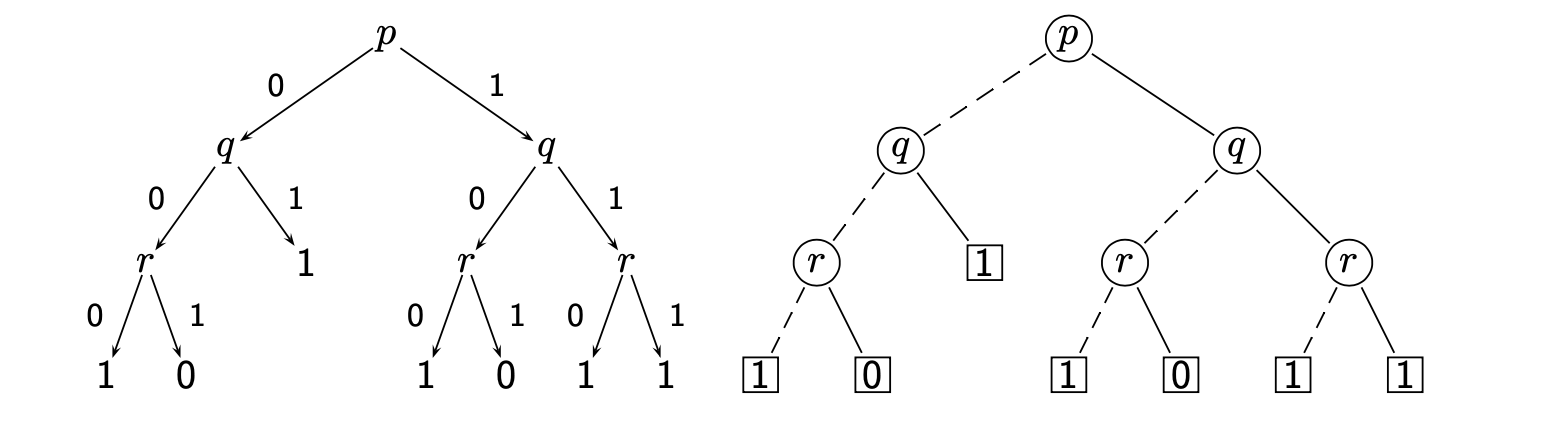
显然地, 二元决策树可被视为分割树的简化表达形式, 且同样具有极其便于检查根节点代表的谓词公式的可满足性的特点.
同时不难看到, 二元决策树完整保留了谓词公式的语义信息 (Semantical Information), 但不保持原谓词公式中可被简化的结构 (也就是原谓词公式中的句法结构). 比如, 公式
和公式
\[\neg \neg((q \rightarrow p) \wedge r \rightarrow (p \leftrightarrow r) \wedge q)\]的二元决策树是相同的. 同一个二元决策树可以对应多个句法结构不同但语义相同的谓词公式.
定义 8.1.1 (二元决策树)
称满足下列条件的树 $d$ 为 二元决策树:
- $d$ 的内部节点由谓词变量标记.
- $d$ 的叶子结点被 $0$ 或 $1$ 标记.
- 每一个内部节点 $n$ 都恰有两个子节点, 且从节点 $n$ 到它的两个子节点的边分别标记为 $0$ 和 $1$. (形式分别为虚线和实线).
- $d$ 中每一条路径上的节点都被 唯一地标记.
需要进一步阐明的是, 二元决策树需满足的性质 $4$ 实际上限定了, 在决策树的每一条路径 (也就是对根节点代表的谓词公式的每一次赋值检验) 上, 公式包含的任何一个谓词变量只能被检测一次, 也就是不允许谓词变量的重复赋值.
8.2 INF 范式
我们在本节中定义谓词公式 (布尔函数) 和二元决策树之间的对应关系.
定义 8.2.1 (INF 范式)
我们如下定义
INF(if-then-else) 范式:\[\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2.\]
- $\top, ~ \perp$ 均为
INF范式中的公式.- 若 $F_1, ~ F_2$ 均为不包含谓词变量 $p$ 的, 位于
INF范式中的公式, 则下列公式也位于INF范式中:
我们可以将 if-then-else 视为一个新的三元联结词, 它等价于:
定义 8.2.2 (给定公式的 INF 范式)
考虑谓词公式 $F, ~ G$, 称 $G$ 为 $F$ 的
INF范式, 若 $G$ 位于INF范式中, 且 $G$ 与 $F$ 等价.
在给出上述的定义后, 我们可将任何一棵二元决策树使用下列的语言表述:
对任一二元决策树中的, 被变量 $p$ 标记的内部节点 $n$, 记其左右子树分别为 $\text{neg(n)}$ 和 $\text{pos(n)}$: 它们分别对应于决策 $p=0$ 和 $p=1$.
定义 8.2.3 (二元决策树的 INF 范式表述)
考虑二元决策树 $d$. 对 $d$ 中的任一节点 $n$, 我们使用下列规则归纳它所表示的谓词公式 $F_n$:
\[F_n \overset{def}{=} \text{if} ~p~ \text{then} ~F_{\text{pos}(n)}~ \text{else} ~F_{\text{neg}(n)}.\]
- 若 $n$ 为 $\boxed{0}$ , 则 $F_n \overset{def}{=} \perp$. 若 $n$ 为 $\boxed{1}$ , 则 $F_n \overset{def}{=} \top$.
- 若 $n$ 为一个由变量 $p$ 标记的内部节点, 则有
我们记通过上述的范式表述所转换得到的谓词公式 $\text{form(d)}$ 为 $F_r$, 其中 $r$ 为二元决策树 $d$ 的根节点. 称 $d$ 为 公式 $F$ 的二元决策树, 若 $F$ 和 $\text{form(d)}$ 等价.
引理 8.2.1
对任意谓词公式 $F$ 和谓词原子 $p$, 公式
\[p\rightarrow F, ~~ p \rightarrow F_{p}^{\top}\]等价, 且公式
\[\neg p\rightarrow F, ~~ p \rightarrow F_{p}^{\perp}\]也等价.
证明
此处我们只考虑第一种情况的证明.
设 $I$ 为某个解释, 首先考虑 $I \nvDash p$ 的情形, 则
\[I \vDash p\rightarrow F, ~~ I \vDash p \rightarrow F_{p}^{\top}.\]故有
\[I \vDash (p\rightarrow F) \leftrightarrow (p \rightarrow F_{p}^{\top}).\]现在考虑 $I \vDash p$ 的情形. 此时有 $I \vDash p \leftrightarrow \top$. 由 等价替换定理 得:
\[I \vDash (p\rightarrow F) \leftrightarrow (p \rightarrow F_{p}^{\top}).\]因此可知, $p\rightarrow F$ 和 $p \rightarrow F_{p}^{\top}$ 等价. $\blacksquare$
推论 8.2.1
对任何谓词公式 $F, G$ 和变量 $p$, 公式:
\[\text{if} ~p~ \text{then} ~F~ \text{else} ~G\]等价于
\[\text{if} ~p~ \text{then} ~F_{p}^{\top}~ \text{else} ~G_{p}^{\perp}.\]
证明
由 INF 范式的定义可知, 公式
等价于
\[(p \rightarrow F) \wedge (\neg p \rightarrow G).\]由 引理 8.2.1: 该式和
\[(p \rightarrow F_{p}^{\top}) \wedge (\neg p \rightarrow G_{p}^{\perp})\]等价. 因此可得原推论结论成立. $\blacksquare$
值得注意的是, 推论中公式
\[\text{if} ~p~ \text{then} ~F_{p}^{\top}~ \text{else} ~G_{p}^{\perp}.\]里的 $F_{p}^{\top}$, $G_{p}^{\perp}$ 均不含谓词变量 $p$, 因此该公式实际上是通过该推论生成的 INF 范式, 我们也可以用该推论直接构造 INF 范式.
定理 8.2.1
任何谓词公式 $F$ 都有一个对应的
INF范式.
证明
我们对 $F$ 中谓词变量的个数应用数学归纳法:
- 若 $F$ 中不含任何变量, 则或 $F \equiv \top$, 或 $F \equiv \perp$. 这两种情况下, $F$ 均有对应的
INF范式: $\top$ 和 $\perp$. -
下面考虑 $F$ 中变量个数不为 $0$ 的情况. 可知, $F$ 等价于
\[\text{if} ~p~ \text{then} ~F~ \text{else} ~F.\]由 推论8.2.1: $F$ 等价于
\[\text{if} ~p~ \text{then} ~F_{p}^{\top}~ \text{else} ~F_{p}^{\perp}.\]并可知公式 $F_{p}^{\top}, ~F_{p}^{\perp}$ 所含的谓词变量数均比 $F$ 小.
由归纳假设可知, 它们分别也有对应的
\[\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2.\]INF范式, 不妨记为 $F_1$, $F_2$. 故 $F$ 等价于
故原命题成立. $\blacksquare$
通过上述定理可知, 要构造一个给定的, 至少包含一个谓词变量的谓词公式 $F$ 的二元决策树, 我们首先需要选定它的一个变量 $p$, 分别为 $F_{p}^{\top}, ~ F_{p}^{\perp}$ 构造决策树 $F_1,~ F_2$ 并继续递归下去, 直到构造出一个以 $p$ 为根节点, $F_1, ~F_2$ 为左, 右子树的决策树. 这样的过程可被总结为下列的算法:
算法 8.2.1 (二元决策树构造算法)
二元决策树构造算法如下图所示. 其中, 参数
select_variable为一个从 $F$ 中挑选谓词变量的函数,simplify为谓词公式的简化函数.

二元决策树的性质可被总结如下:
- 谓词公式 $F$ 的二元决策树大小的增长速度是关于谓词公式本身大小的 指数级别.
- 对用二元决策树表示的谓词公式的可满足性检测花费的时间相比公式本身大小的增长速度为 常数级别.
- 二元决策树不能被用来有效地检测公式的等价性.
- 我们不能对二元决策树进行有效的逻辑运算.
8.3 二元决策图
二元决策图是二元决策树通过消除两种冗余而得到的:
定义 8.3.1 (二元决策图)
二元决策图为一个满足下列两条性质的二元决策树 (有根节点的有向无圈图):
- 树中每个节点的左右子图均不同.
- 对全体子树而言, 任一对子树都是 不同构 的, 也就是说它们的形式不得相同.
上述两条规则决定, 有向无圈图 (DAG, Directed Acyclic Graph) $d$ 不包含对任何变量的重复赋值 (也就是重复测试), 也不包含任何同构的子图.
我们可以通过如下的两种变换将任意的二元决策树转换为二元决策图:
- 冗余测试消除规则:
若存在节点 $n$, 使 $\text{neg}(n)$ 和 $\text{pos}(n)$ 为相同的有向无圈图, 则删除该节点: 将节点 $n$ 所在的位置替换为 $\text{neg}(n)$. - 同构子图融合规则:
若位于两个 不同节点 $n_1$, $n_2$ 的子图是同构的, 则将这两个子图融合: 删除其中一个, 并将原先所有指向被删除子图的根节点的边重定向到另一子图的根节点处.
二元决策图的基本性质总结如下:
- 谓词公式 $A$ 的二元决策图大小的增长速度是关于谓词公式本身大小的 指数级别.
- 与二元决策树相同, 对用二元决策图表示的谓词公式的可满足性检测花费的时间相比公式本身大小的增长速度也为 常数级别.
- 二元决策图同样不能被用来有效地检测公式的等价性.
- 我们同样不能对二元决策图进行有效的逻辑运算.
8.4 有序二元决策图
和在上一章中介绍的 语义树 相似, 任何公式的二元决策图都受到对其变量测试的先后顺序的影响: 如果我们尝试对公式中的第一个变量先进行赋值测试并构造二元决策图, 这样的图很可能和我们先选择最后一个变量时构造的图在大小和结构上都有显著差别.
为了确保决策图的唯一性, 我们对谓词公式中出现的所有谓词变量引入 顺序 的概念. 通过人为限制构造决策图时测试变量的先后顺序, 我们可以确保这样构造出的二元决策图一定是唯一的.
定义 8.4.1 (有序二元决策图)
令 $>$ 为对谓词变量的线性偏序, 记 $d$ 为一个二元决策图. 若对每个由变量 $p_1$ 所标记的节点 $n_1$, 设其子节点 $n_2$ 由变量 $p_2$ 标记, 则 $p_1 > p_2$, 则称这样的二元决策图为 有序的.
我们下面说明, 对给定谓词公式 $F$, 在限定组成它的谓词变量的顺序后, 它的 OBDD 必是唯一的:
引理 8.4.1
考虑谓词变量 $p$ 和不包含 $p$ 的谓词公式 $F_1, F_2, G_1, G_2$. 则:
\[(\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2) \equiv (\text{if} ~p~ \text{then} ~G_1~ \text{else} ~G_2)\]当且仅当
$F_1 \equiv F_2$ 且 $F_2 \equiv G_2.$
证明:
必要性: 设
\[(\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2) \equiv (\text{if} ~p~ \text{then} ~G_1~ \text{else} ~G_2),\]要证 $F_1 \equiv G_1$, $F_2 \equiv G_2$ 亦然. 我们下面通过说明 $F_1$, $G_1$ 的模型相同达成这一点.
取 $F_1$ 的某个模型 $I$. 定义 $I’$:
\[I'(q) \overset{def}{=} \begin{cases} I(q) ~~ \text{if}~p \neq q \\ 1 ~~~~~~~ \text{if}~p=q\end{cases}.\]显然知 $I’ \vDash F_1$. 由 $I’ \vDash p$ 且 $I’ \vDash F_1$, 我们同时有
\[I' \vDash \text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2.\]同时由
\[(\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2) \equiv (\text{if} ~p~ \text{then} ~G_1~ \text{else} ~G_2)\]可得:
\[I' \vDash \text{if} ~p~ \text{then} ~G_1~ \text{else} ~G_2.\]由上式以及 $I’\vDash p$ 可知: $I’ \vDash G_1$. 由于 $G_1$ 中不包含变量 $p$, 由 $I’$ 定义知: $I \vDash G_1$.
由此可知, $F_1$ 的任一模型都是 $G_1$ 的模型. 对称地, 我们同样可证 $G_1$ 的任一模型都是 $F_1$ 的模型.
充分性: 设 $F_1 \equiv G_1$, $F_2 \equiv G_2$. 由等价替代定理可得:
\[(\text{if} ~p~ \text{then} ~F_1~ \text{else} ~F_2) \equiv (\text{if} ~p~ \text{then} ~G_1~ \text{else} ~G_2). \blacksquare\]定理 8.4.1 (OBDD 的权威性)
记 $d_1, ~d_2$为谓词公式 $F$ 的两个
OBDD, 则它们是同构的.
我们下面给出将节点 融合 入 OBDD 和构造 OBDD 的算法:
算法 8.4.1 (OBDD 节点融合算法)
该算法步骤如下图所示:

算法 8.4.2 (OBDD 构造算法)
该算法步骤如下图所示:

注: 具体的解题过程详见教材 $145-148$ 页.
8.5 有序二元决策图的运算
与二元决策图不同, 我们可以对有序二元决策图进行 逻辑运算. 一般地, 对谓词公式的有序二元决策图的逻辑运算可以总结为下列算法:

我们下面给出两个例子: 对二元决策图的 合取 与 析取:


