经典规划
在本章中, 我们考虑较复杂的规划问题. 我们将在第一节中引入一种可用于表示规划问题的语言, 在第二节中介绍 前向搜索算法 和 后向搜索算法, 在最后一节中介绍如何使用 规划图 这一数据结构高效地搜索规划.
1. 定义经典规划
在本章中, 我们使用 要素化表示 (Factored Representation): 用变量表示规划问题的不同状态的表示方法, 对我们的规划问题进行建模.
进一步地, 我们使用一种简单化的 PDDL 语言 (Planning Domain Definition Language) 描述用于定义搜索问题的 四要素: 初始状态, 当前状态下的可用动作, 某个动作应用后的结果, 以及目标测试.
在我们的 PDDL 中, 每个状态表示为 流 (Fluent, 也就是无变量, 无函数的原子, 表示某个用于描述状态的, 不可再分的基础元素, 可以类比谓词逻辑的原子公式) 的 合取.
同时, 我们的 PDDL 使用数据库语义, 也就是说任何没有在状态中提到的流都不为真.
在一个 状态 中, 包含变量的流, 形为否定式的流 以及 使用了函数符号表示的流 都不可被包含在其中.
在对 状态 建模时, 我们需要精心地设计 状态的表示, 从而使状态能够表示为 多个流的合取, 进而我们可以用 逻辑推理 操作它. 我们也可以将状态的表示设计为 流的集合, 并使用 集合运算 操作它.
在对 动作 建模时, 我们可以用 定义了动作的前提和效果 的一组模式来描述. PDDl 通过指出 哪些东西发生了变化 来描述动作的结果, 而不提及其它任何不受动作影响的东西.
动作的 前提 和 效果 都是 文字 (Literal, 正或负的原子语句, 定义和谓词逻辑中的相同) 的 合取:
前提 定义了 “能够使动作被执行” 的条件, 而 效果 定义了执行这个动作的结果. 我们称: 动作 $a$ 能在状态 $s$ 时被执行, 若 $s$ 蕴含了 $a$ 的前提. 同时, 若状态 $s$ 满足 $a$ 的前提, 称 在 $s$, $a$ 是适用的 (Applicable).
在状态 $s$ 执行动作 $a$ 的结果定义为状态 $s’$, 它也由一组流表示. 通过从 $s$ 中 去除在动作效果中以负文字出现的流 (也就是除去因动作执行而不再成立的事实), 并 增加在动作效果中以正文字出现的流 (即添加因动作执行而成立的事实), 我们就得到了 $s’$.
需要注意的是: 在 PDDL 中, 动作状态中的时间和状态是 隐式的: 效果 总是指向 前提 后的那一个时刻.
我们可以用一组动作模式定义 规划域. 在这个域中, 一个特定问题用一个初始状态加上一个目标来定义. 若我们能找到某个 动作序列 使得从初始状态开始, 通过执行这个序列能够在一个 蕴含了目标 的状态 $s$ 结束, 实际上这个特定问题就得到了解决.
经过上述的讨论, 显然易见我们将规划定义成了一个搜索问题.
2. 前向和后向搜索算法
在本节中, 我们讨论状态空间的搜索规划算法.
2.1 前向 (前进) 状态空间搜索
由于我们已经将规划问题转换为了一个搜索问题, 我们可以使用启发式搜索算法或其他搜索算法 从初始状态出发 求解规划问题.
在应用中, 我们通常结合实际人为地定义在任何一步上执行任何一种可行的新行为的 成本 (Cost), 结合启发式算法 (如分支定界或 $\text{A}^*$ 算法) 解决问题, 否则算法在每一步上都需要枚举所有可能的行为, 导致搜索规模过于庞大.
2.2 后向 (后退) 状态空间搜索
在后向搜索中, 我们从 目标 出发, 从后往前地应用动作, 直到找到能够达到初始状态的步骤序列.
我们的搜索从 目标: 对一组状态进行描述的文字的合取 开始. 我们首先要将所有已知的动作 “取逆”, 也就是将它们分别 转换为后退动作. 由于我们此前在 PDDL 中的设计, 我们只需要对每个已知动作构造一个对应的新的动作, 令这一动作 增加的效果不必在前一时刻为真, 而原动作的前提在前一时刻必须成立 即可.
也就是说, 给定一个基元目标描述 $g$ 和动作 $a$, 从 $g$ 通过 $a$ 回退到 $g‘$, 可定义为
\[g' = (g - \text{ADD}(a)) \cup \text{Precond}(a)\]需要注意的是, 在上述公式中并未提及 $\text{DEL}(a)$, 因为 我们并不知道 $\text{DEL}(a)$ 中的流在动作 $g$ 之前是否为真, 因此没有必要提及它.
同时, 对于给定的节点 $v$, 该节点的目标描述记为 $\text{goals}(v)$, 则在该节点处可后退的动作 $\alpha$ 满足下列条件:
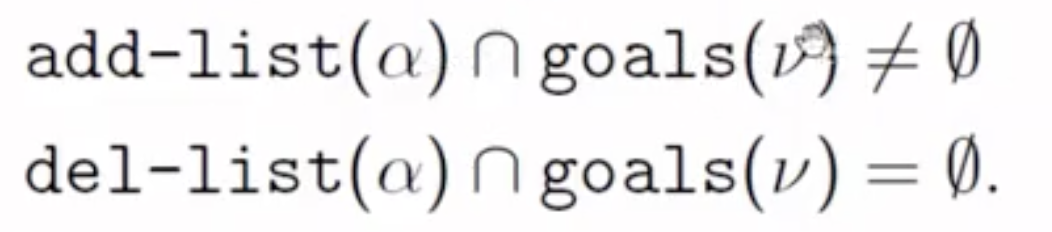
随后, 我们需要决定哪些动作是后退的 候选动作. 在前向搜索中, 我们选择的候选动作是那些 适用的 动作, 而在后向搜索中, 我们需要选择 相关的 (Relevant): 导致 当前目标状态的规划中可以作为最后一个步骤 的那些动作.
我们在搜索中, 持续选定那些 相关的, 明显对将当前状态反向转换为贴近目标状态 (在这里也就是初始状态) 的动作, 从后往前搜索, 最终也可以得到一条能够达到初始状态的步骤序列.
2.3 Means-End Approach
我们还可以通过分步解决 Goal 的方式求解问题:

其实质是:
选择一个 执行后效果是 $G$ 的一部分 的操作 $\alpha$, 先找到某个能从初始状态开始到达某个满足 $\alpha$ 的前束条件状态的执行计划 $\pi$, 然后再找一个从 $\alpha$ 执行完状态开始可以到达最终目标状态 $G$ 的执行计划 $\pi’$, 从而 $\pi; \alpha; \pi’$ 就是一个可以确保满足目标的执行计划.
显然在执行 $\pi; \alpha$ 后 原问题目标的一部分: $\text{add-list}(\alpha)$ 得到了满足. 而 $\pi’$ 则确保了目标中需要被满足的剩下的子目标 $G \backslash \text{add-list}(\alpha)$ 得到满足. 这也就是 $\alpha$ 的效果必须包含 $G$ 的一部分的原因. 若 $\alpha$ 对满足 $G$ 毫无贡献, 则永不可能构造出以 $\alpha$ 为分界的子问题.
3. 规划图
在本节中, 我们给出一个可以给出更好的启发式估计的, 称为 规划图 (Planning Graph) 的数据结构.
规划问题向我们提出的要求是, 我们能否从初始状态出发达到目标. 不妨假设记录了 从初始状态到后继状态, 进而到 “后继状态的后继状态” 的所有行动的树 (类比谓词逻辑中的决策树), 我们只需要检索这棵树就可以确定这个要求能否被满足. 虽然这一方法会在应用中由于树的大小是 指数级别 而不切实际, 我们可以通过构造出 对这棵树的多项式大小的估计: 规划图, 来估计出从某个状态 $S_0$ 达到目标 $G$ 需要执行的步数.
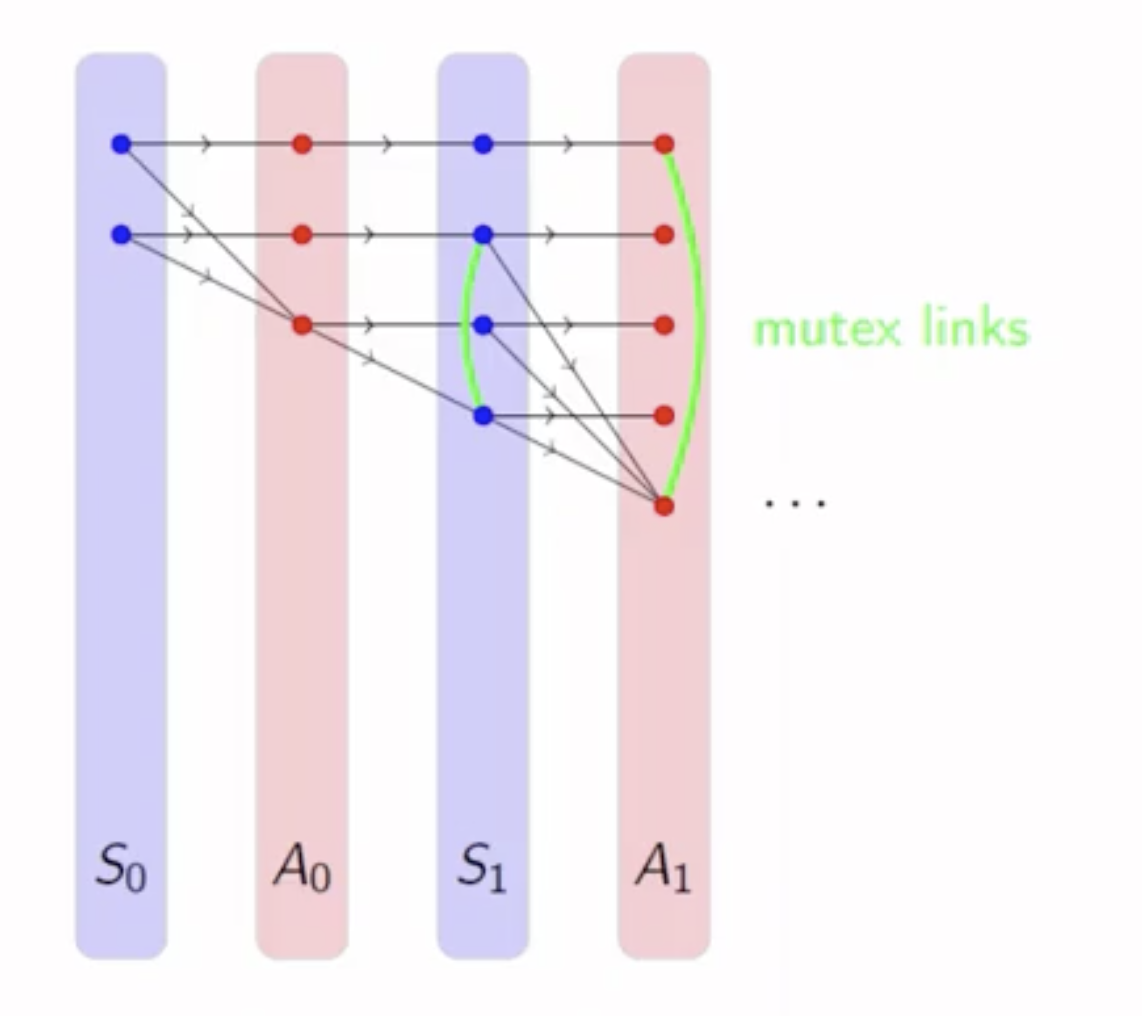
规划图 是由有向图层叠而组织起来的: 它的结构首先是初始状态层 $S_0$, 由 在 $S_0$ 成立的每个谓词文字 $p$ 和 所有在 $S_0$ 不成立的谓词文字 $p$ 的取反 $\neg p$ 组成; 其次是层次 $A_0$, 由在 $S_0$ 适用的每个基元动作节点组成; 随后是层次 $S_1$, 由 $A_0$ 中所有动作节点的效果 (不同的动作可能导致新的谓词文字成立, 也可能导致原本成立的不再成立) 组成 , 后面紧跟 $A_1$, 然后是 $S_2$…, 这样的迭代会持续下去, 直到规划图 稳定 为止: $S_i$ 不再发生任何变化.
需要注意, 一旦某个谓词文字在某个状态层 $S_i$ 成立,它就会在规划图中后面的任何一个状态层中均保持成立.
我们同时会在每一个状态层和动作层上基于下列原则标记该层中 互斥 的谓词文字或动作:

由于在规划图中无论是状态层还是动作层的大小都在单调递增, 而在任何系统中可被建模的状态和动作都是有限的, 因此任何规划图必然都能最终达到稳态, 也就是说它是 有限的.
在规划图达到稳态之后, 我们就可以拿着问题的目标态所需要满足的条件列表对规划图的每一个状态层进行对比, 由此可以进一步地得到:
- 实现目标列表 $G$ 中某个子目标 $g$ 所需要花的 最小 步数 (
Under-estimate). - 实现目标列表中所有子目标所需要花的 最小步数 (也就是 $G$ 中所有子问题 $g$ 所需步数的最大值).
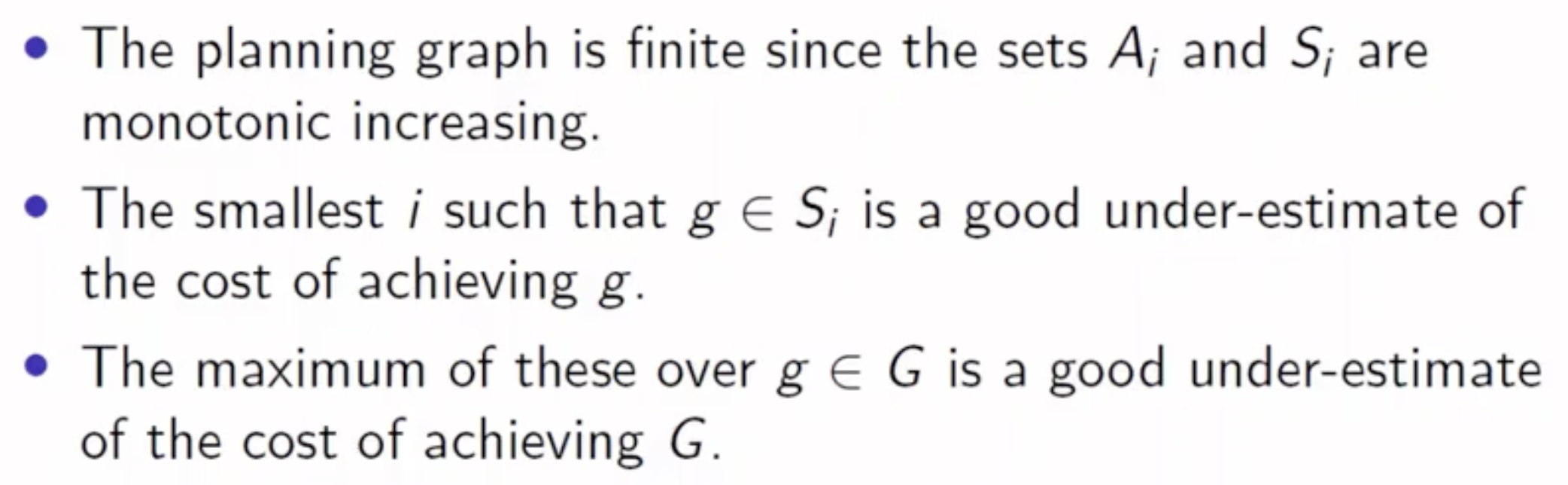
4. 补充: Planning with Logic


注: 所有涉及行为的谓词都在 do 里面, -> 前后的谓词都要标记state

frame problem: the challenge of representing the effects of action in logic without having to represent explicitly a large number of intuitively obvious non-effects.
qualification problem: the qualification problem is concerned with the impossibility of listing all the preconditions required for a real-world action to have its intended effect.
