对抗搜索算法
在本章中, 我们将对 包含两个竞争的决策者的对抗式决策 问题建模, 并介绍数个用于为这样的问题找出可行解的算法: 对抗搜索算法 Mini-Max Search, 并进一步地介绍它的剪枝优化版本: Alpha-Beta Pruning.
对抗搜索问题
我们考虑 由两个智能体 之间, 信息透明且对等 的, 通过 竞争 实现的 零和博弈 问题. 称这样的问题为 对抗搜索问题.
这样的决策问题有两方参与者, 彼此为 你死我活 的竞争关系, 一方得利必然导致另一方失利, 且两方所得到利益的总和永远为 $0$. 此外, 信息对于双方而言都是透明对等的, 交战双方由此为依据作出合理决策, 目标为让自身利益最大化, 从而赢得游戏.
我们接下来会介绍两种算法: Mini-Max (最小最大) 算法, 以及 Alpha-Beta 剪枝算法.
Mini-Max 算法
我们以标准的棋类游戏 (围棋, 奥赛罗棋, 象棋等) 说明该算法. 此算法的核心是, 假设对手始终理性最大化, 一定能在任何局面下作出对自身最优的决策. 因此通过定义某个对当前局势的 “评价”, 算法所服务的 “我方” 目标即为, 在上述假设的基础上, 尽可能地选择让对手最终所得最小化 的决策, 也就是 “在假设对手总会最小化我方得利的前提下 (Mini), 尽可能地选择能让自身利益最大化的决策 (Max)”.
这样的决策过程同样可以使用 决策树 表示. 这样的决策树具备一系列共同特征:
- 图中的节点代表棋局的某一状态, 且基于执子方的不同而被分为两类: 由我方执子的
Maximizing Node: 算法需要在这样的棋局下选择 最大化 我方利益的决策, 以及由对方决策的Minimizing Node: 算法需要模拟对方, 在这样的棋局下选择 最小化 我方利益的决策. - 图中的边代表在上一状态下作出的某种决策. 边所连接的两个节点之间的关系是: 从上一节点, 通过执行边所代表的决策, 状态转移为新的节点.
在不考虑计算机运算能力限制的前提下, 显然基于当前棋局下, 所向下推演所得到的最终局势反推, 才能够得到真正意义上的最优解. 实际上, 为了让算法能够在可接受的时间内执行完毕, 我们会定义一个 递归最大深度, 限制程序所能够向下查找的决策步数.
由于对抗决策问题 回合制 的特性, 算法每一次执行得到的结果只是 相对最优的, 下一步的决策. 从最底层向上考虑, 对属于某一层的节点的打分只会有下列三种情况:
- 考虑的是底层节点, 由于不能再继续向下检索, 程序只能直接返回节点本身的打分值.
- 考虑的是位于中间层的
max节点. 为了最大化我方利益, 所返回的是子节点中的 最大分数. - 考虑的是位于中间层的
min节点. 为了最小化我方利益, 所返回的是子节点中的 最小分数.
因此, 我们采用 递归调用 的方式实现自底向下上的最优解评分.
1
2
3
4
5
6
7
8
9
def miniMaxValidation(Node, Depth):
if Depth == 0:
return staticValue(Node)
else if Node.isMaximizing() == true:
compute miniMaxValidation(Daughter, Depth-1) for each daughter
return the MAXIMUM among all results
else
compute miniMaxValidation(Daughter, Depth-1) for each daughter
return the MINIMUM among all results
基于上述算法, 我们可以得到某个节点的评分, 该评分所表示的是遵循算法的假设时, 我们所能得到的最大利益. 因此, 为了选出 相对最优的, 下一步的决策, 我们还需要在 miniMaxValidation() 上再包装一层函数进行对节点的选择:
1
2
3
4
5
6
7
def miniMaxhelper(Node, Depth):
if Node.isMaximizingNode == true:
compute miniMaxValidation(Daughter, Depth-1) for each daughter
return THE MOVE WHICH LEADS TO A MAXIMUM VALIDATION
else:
compute miniMaxValidation(Daughter, Depth-1) for each daughter
return THE MOVE WHICH LEADS TO A MINIMUM VALIDATION
将 miniMax 评价函数和 miniMax 外层包装函数结合, 我们就得到了完整的 MiniMax 算法实现.
显然, 在决策树有限的情况下, MiniMax 算法是完备的. 基于 “对手绝对理性” 的假设, MiniMax 算法也一定能给出假设下的最优结果.
我们记决策树的最大深度为 $d$, 决策树考虑范围内节点上有效走法 (有效决策) 数量的最大值为 $n$, 则由于 MiniMax 算法本质上是单纯的深度优先搜索, 其时间复杂度为 $O(n^d)$.
MiniMax 算法是一种简单有效的对抗手段, 由于考虑到了决策中的最坏情况, 因此即使对手犯错也能得到一个不错的解, 若对手完全理性则能返回最优结果. 但搜索树的规模严重影响算法的运行时间. 为了缓解这一问题, 就必须要对搜索树剪枝.
Alpha-Beta 算法
Alpha-Beta 算法本质上是对 MiniMax 算法的剪枝改进版本, 不同之处在于 Alpha-Beta 会维护 根结点基于已进行的搜索结果所知的我方的理论最高收益 和 对方基于已进行的搜索结果所知的对我方的理论最大伤害. 在递归计算每一个节点的评价时, 算法会将每一个节点的评价和已知最优解进行比较, 从而及时 丢弃 对 进一步更优化已知解无益 的决策分支, 也就是 剪枝.
通过对 miniMax 评价函数作下述修改, 我们就能完成对 Alpha-Beta 算法的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def miniMaxValidationwABPruning(Node, Depth, alpha, beta):
if Depth == 0:
return staticValue(Node)
else if Node.isMaximizing() == true:
alpha = NEGATIVE.INFINITY
for each Daughter in Node.daughters():
alpha = max(alpha, miniMaxValidation(Daughter, Depth-1, alpha, beta))
if alpha >= beta:
break
return alpha
else
beta = POSITIVE.INFINITY
for each Daughter in Node.daughters():
beta = min(alpha, miniMaxValidation(Daughter, Depth-1, alpha, beta))
if alpha >= beta:
break
return beta
注意此处的记号. 对于每一个节点, 我们都使用 alpha 和 beta 值分别表示当前基于现有的搜索结果已知的, 该节点能够给予我方利益的 下界 和 上界. 通过对每一个子节点时相应地对它们进行修正, 我们就可以在递归中一直更新并维护这两个作为剪枝依据的关键数据.
在 Maximum 节点下, 由于算法基于己方利益考量, 故此处做出的选择不可能进一步恶化现有的理论最大利益, 因此 Maximum 节点能且只能更新和维护表示下界的 alpha 值.
在 Minimum 节点下, 由于算法基于对方利益考量, 故此处做出的选择不可能进一步放大我方现有的理论最大利益, 因此 Minimum 节点能且只能更新和维护表示上界的 beta 值.
同样的, 在任何情形下一个有价值的解中都不可能出现 alpha >= beta 的情况. 因此, 该情形若出现, 我们就可以终止搜索, 执行剪枝.
得益于剪枝, Alpha-Beta 算法 (一般) 能够更快地给出假设下的最优解.
上面的解释可能艰深晦涩, 难以理解. 我们下面来看一个例子, 希望能够对各位有所启发 (此处强烈感谢王老师):
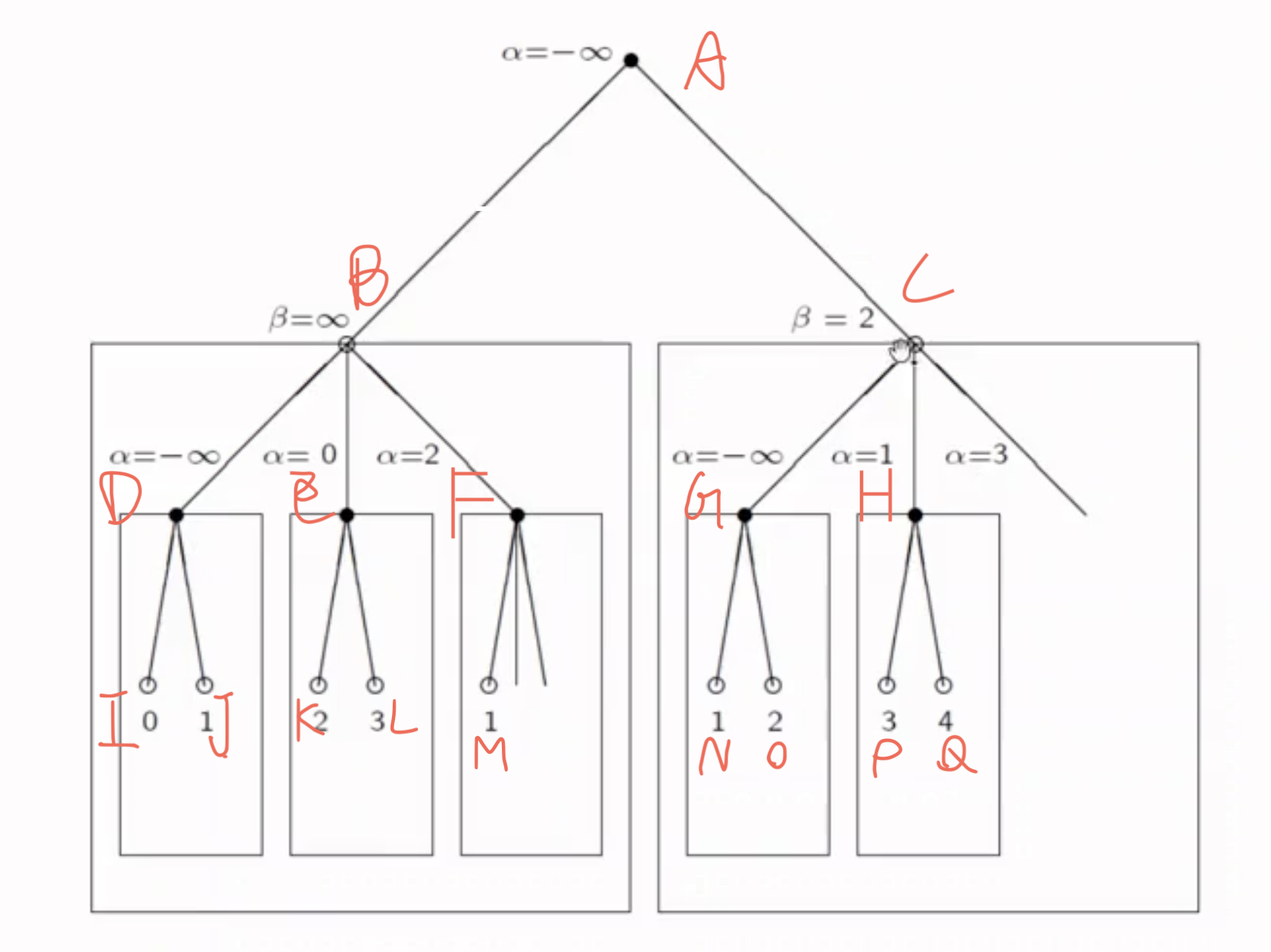
我们考虑课上的Slides提到的例子, 逐步解释 Alpha-Beta Pruning 是如何用于解决该题, 并且执行剪枝的:
Alpha-beta Pruning 执行的搜索是 自顶向下递归, 深度优先 的. 首先可看出第 $1, 3$ 层为 Minimizing Node, 第 $2, 4$ 层为 Maximizing Node.
在图中的 每个节点 上, 都会相应地维护 它们自己的 $\alpha, \beta$. 其中, $\alpha$ 表示利益下界, 如果不从父节点继承的话初始化为 $-\infty$, 而表示利益上界的 $\beta$ 节点值若不从父节点继承的话被初始化为 $\infty$.
我们的搜索从根节点 $A$ 开始. 由于根节点是 Minimizing Node, 它的目的是维护 $\beta$ (取得该节点上判断的 $\beta$ 的最小值, 因此该节点的 $\beta$ 需要被初始化为 $\infty$. 又因为它没有父节点, 因此对它来说, 有: $\alpha = -\infty$.
从根节点 $A$ 向下遍历它的第一个子节点 $B$. 由于 $B$ 是 Maximizing Node, 它的目的是维护 $\alpha$ (取得该节点上判断的 $\alpha$ 的最大值, 因此该节点的 $\alpha$ 需要被初始化为 $-\infty$. 而该节点的 $\beta$ 从父节点继承, 因此对它来说, 有: $\beta = \infty$.
基于深度优先搜索思想, 我们再遍历 $B$ 的第一个子节点 $D$. 由于 $D$ 是 Minimizing Node, 它的目的是维护 $\beta$ (取得该节点上判断的 $\beta$ 的最小值, 因此该节点的 $\beta$ 需要被初始化为 $\infty$, 而 $\alpha$ 从 $B$ 继承, 值为 $-\infty$.
$B$ 更新 $\beta$ 的方式是: 基于深度优先思想遍历其子节点, 选取子节点评分里最小的那一个作为 $\beta$ 的值. 显然我们第一个遍历到的子节点是 $I$. $I$ 是 Maximizing Node, 它的目的是维护 $\alpha$ (取得该节点上判断的 $\alpha$ 的最大值, 因此该节点的 $\alpha$ 需要被初始化为 $-\infty$. 而该节点的 $\beta$ 从父节点继承, 因此对它来说, 有: $\beta = \infty$. 由于自身评分为 $0$, 它自己的 $\alpha$ 被更新为 $0$. 由于自身已经是叶子节点, 因此达到最高递归深度, 开始回溯.
在回溯时, 将 $I$ 的 $\alpha$ 的值作为该节点的评分. 由此可知在将 $I$ 和 $D$ 的 $\beta$ 值比对时, $0 < \infty$, $D$ 的 $\beta$ 值暂时被更新为较小的 $0$. 回溯到 $D$ 节点后继续遍历另一分支 $J$, 由于 $J$ 的评分为 $1$, 因此 $D$ 的 $\beta$ 值保持为 $0$.
至此 $D$ 这一支子树已经遍历完成, 继续回溯到 $B$. 将 $D$ 和 $B$ 做比较, 由于 $D$ 是 Minimizing Node, 取它的 $\beta$ 值作为它的评分. 因此可知 $B$ 的 $\alpha$ 值暂时被更新为 $0$.
继续遍历另一分支 $E$, 不难看出在遍历完该分支后, $B$ 的 $\alpha$ 值被更新为 $3$.
此时再从 $B$ 开始遍历 $F$. 由于此时 $B$ 节点的 $\alpha = 2, \beta = \infty$, $M$ 的评分为 $1$, 因此得出 $F$ 有 $\alpha=2, \beta=1$, 显然违背了 $\alpha < \beta$ 的条件. 因此分支 $F$ 是一个非法分支, 需要从 $M$ 处开始剪枝, 搜索到此为止.
至此以 $B$ 为根节点的子树已经全部搜索完毕, 下面需要将 $B$ 的评分 $2$ (因为 $\alpha=2$) 回传到根节点 $A$ 处用于更新根节点的 $\beta$ 的值.
基于更新规则可知根节点的 $\beta$ 被更新为 $2$. 然后, 我们带着更新后的 $\beta$ 遍历到 $C$, 此时 $C$ 满足 $\alpha=-\infty, \beta=2$. 同样地对 $C$ 的子节点执行深度优先搜索并使用同样的方法判断每个子节点的评分并回传给父节点更新父节点的 $\alpha$ 或 $\beta$ 值, 在遍历完节点 $H$ 后可得 $C$ 此时满足 $\alpha=3, \beta=2$. 由于此时再度违背了 $\alpha < \beta$ 的条件, 因此从此开始我们从节点 $C$ 的第二棵子树 $H$ 处开始剪枝, 不再搜索剩下的子树.
