Prolog 入门: 剪枝与回溯
在本章中, 我们将介绍一个新的用于剪枝 (Cut) 的内置谓词 !, 并解释如何使用它控制 Prolog 的回溯行为.
随后我们将介绍回溯谓词 fail, 并介绍剪枝谓词和它的联合应用: negation as faiulure.
1. 剪枝谓词 Cut
Prolog 的证明搜索机制高度依赖自动化的回溯算法, 但基于预置规则的回溯行为有时可能会导致遍历了完全没有必要遍历的内容, 降低程序的运行效率.
在第三章中我们已经了解到, 通过调节规则和目标的顺序, 我们可以一定程度地影响 Prolog 证明搜索的行为. 本节将介绍一个 Prolog 内置谓词: 剪枝谓词 (Cut), 它可用于人为终止 Prolog 的回溯和证明搜索行为, 从而为我们提供对程序行为更精细的控制.
Cut 的占位符为 !, 它是一个可被直接写入子句中的原子谓词:
1
axton(X) :- rhythm_gamer(X), proficient_developer(X), !, android_user(X), windows_user(X).
剪枝谓词 Cut 具如下性质:
- 在证明搜索过程中若它被视为目标, 则它为一个 永远被满足的目标.
- 考虑某个子句 $\alpha$ 包含了剪枝谓词
!. 则在某次为了尝试满足目标 $G$ 的证明搜索尝试联合该子句时, 剪枝谓词会 直接将自目标 $G$ 和包含子句的规则左侧联合之前所执行的所有选择, 包括对这个特定子句 $\alpha$ 的选择作为查询的结果提交, 即使联合失败程序也不会再尝试新的规则或变量.
我们来看下面的一个例子.
1
2
3
4
5
6
7
p(X) :- a(X).
p(X) :- b(X), c(X), d(X), e(X).
p(X) :- f(X).
a(1). b(1). c(1).
d(2). e(2). f(3).
b(2). c(2).
我们若查询 p(X) 可得:
1
2
3
4
5
6
?- p(X).
X = 1 ;
X = 2 ;
X = 3.
false
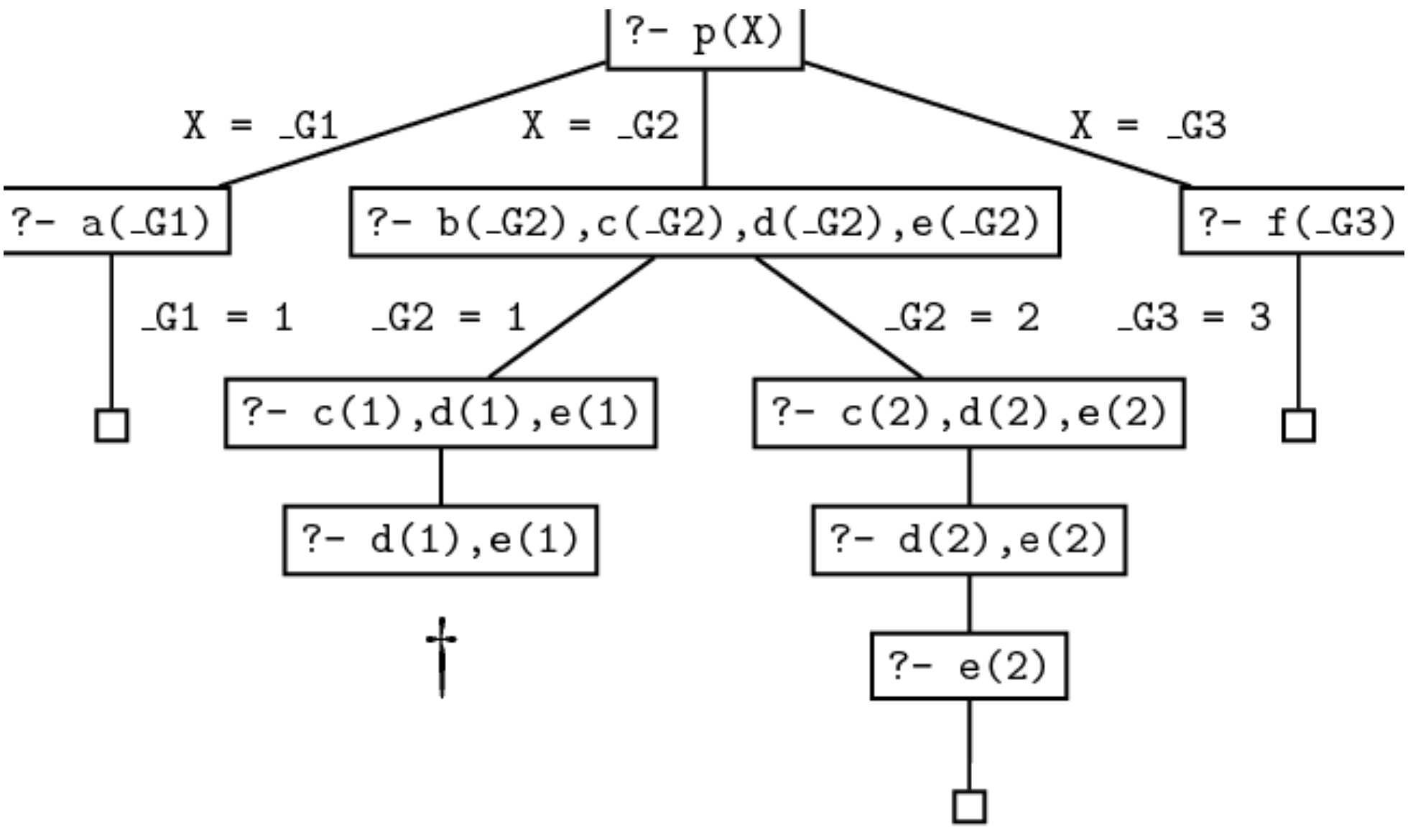
我们在执行证明搜索时,搜索树如下图所示. 可见 Prolog 在处理第二条规则时执行了一次回溯:
我们下面对第二条规则进行简单改动:
1
p(X) :- b(X), c(X), !, d(X), e(X).
则此时我们若执行同样的查询, 返回的结果如下:
1
2
3
?- p(X).
X = 1 ;
false.
可见 Prolog 不再为我们提供另两个可行解. 下面我们分析程序的执行流程来解释这一现象的成因.
- 在程序执行伊始
Prolog尝试首先联合第一条规则, 因此我们得到目标a(X). 通过检索知识库将a实例化为 $1$, 程序即可将a(X)和事实a(1)联合, 从而找到第一个可行解X=1. 到此为止新程序的执行流程和原先没有任何差别. - 下面
Prolog会尝试联合第二条规则, 而得到目标序列b(X),c(X),!,d(X),e(X). 由于Prolog顺着知识库中事实排序尝试联合变量X, 此次尝试还是会从X=1开始. 联合的结果使得我们满足了目标序列中的前两个子目标, 此时的目标序列变为!,d(X),e(X). - 我们对第二条规则的修改在此处真正生效. 由于
!被视为一个自动被满足的目标, 因此程序会提交我们此前做出的选择X=1和我们当前对第二条规则的选择, 跳过!并尝试联合下一个子目标d(X). - 由于无法从知识库中找到满足目标的事实
d(1), 此次联合失败, 并且我们找不出任何能够满足该子目标的其他方法. 由于Prolog在处理内置谓词!时已经将我们在这一轮证明搜索中对事实和规则的选择提交, 程序不再被允许回溯并重新选择事实b(2)进行联合, 也更不会被允许回溯到原点选择第三条规则进行联合, 因此我们只能得到在第一轮联合中得到的唯一解X=1.
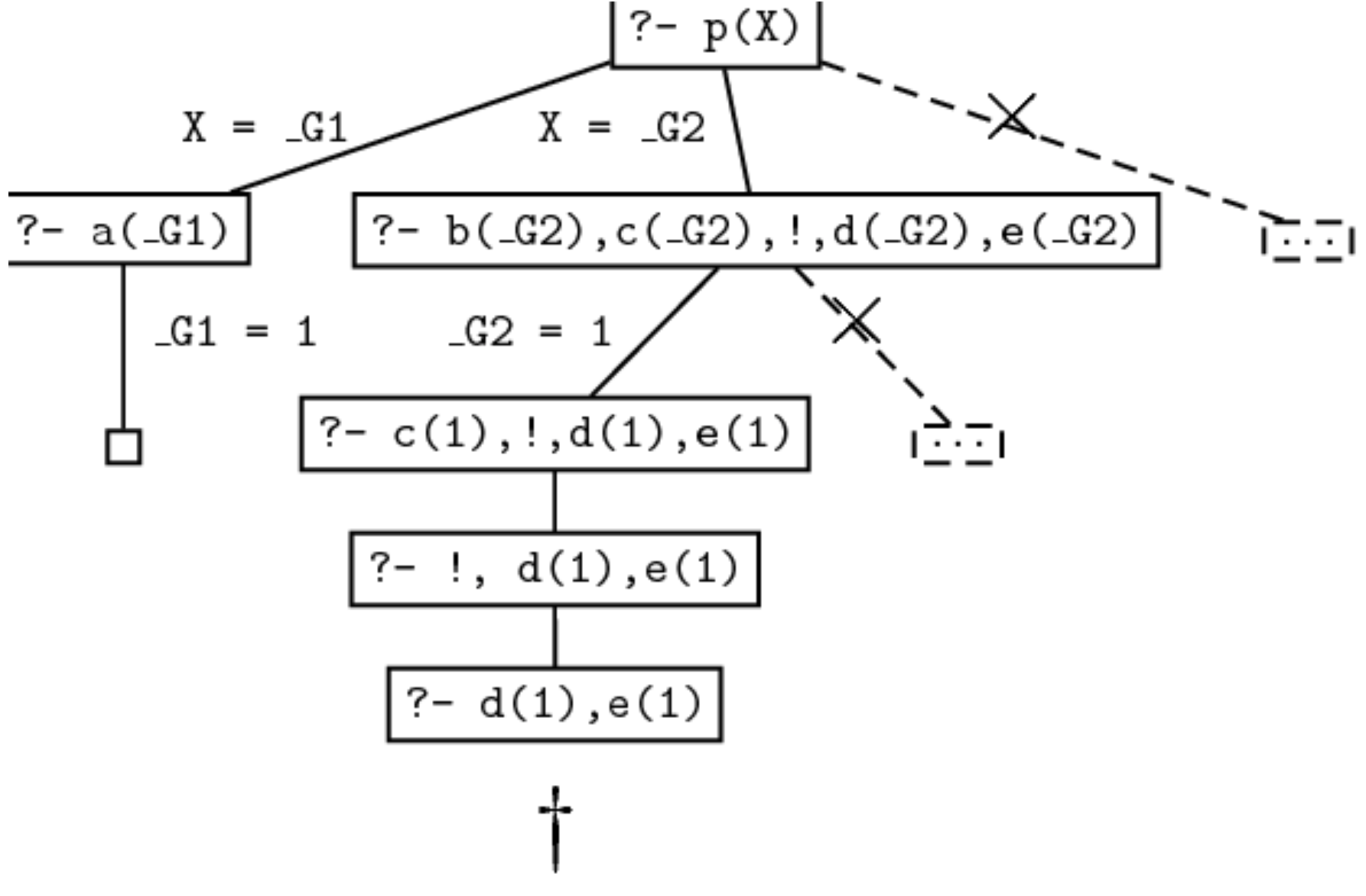
在这里需要注意一点. 剪枝谓词 Cut 实质上移除的仅仅是程序回溯到该谓词左侧以及更低一层地, 作出尝试联合母子句那一层的可能, 而不会限制比它更深层级的回溯. 举例而言, 考虑规则
1
q:- p1,...,pn, !, r1,...,rm
则谓词 ! 并不会限制程序在 r1, ..., rm 中的任何回溯.
2. 对剪枝谓词的利用
我们下面讨论对剪枝谓词的利用. 考虑下列的例子:
1
2
max(X,Y,Y) :- X =< Y.
max(X,Y,X) :- X > Y.
我们定义了一个三元谓词 max/3, 用于检查第三个元素是否 恰好 为第一个和第二个元素中更大的哪一个.
该程序显然可以正常执行被设计的功能, 但不包含剪枝谓词的设计可能导致较低的执行效率. 考虑第三个元素恰好为最大元的情况, 此时程序会尝试执行完全没有执行必要的, 和已经被满足的第一条规则实际上互斥的第二条规则, 显然这纯粹是浪费时间.
我们所希望的是, 若满足第一条规则, 则不应该再去执行第二条. 通过如此修改程序我们就可以实现这一点:
1
2
max(X,Y,Y) :- X =< Y, !.
max(X,Y,X) :- X > Y.
对该程序的过程式描述如下:
程序首先尝试从知识库中联合第一条规则, 若第一条规则蕴含的目标不可被满足 (也就是Y不是最大元), 程序尝试联合第二条规则并得到可行解.
若程序在联合第一条规则时即可满足子目标 X =< Y, 由于剪枝谓词的存在当前的一切选择会被提交为查询结果, 程序在联合完成后就会终止而不会尝试徒劳地联合第二条规则.
显然, 我们在这一例子中加入的剪枝谓词在不改变程序原本功能的前提下实现了对程序执行效率的优化. 这样的剪枝谓词被称为 安全剪枝 (Green Cuts).
我们下面考虑第二个优化的例子. 看上去我们可以去除第二个规则查询符号右侧的数值大小判断:
1
2
max(X,Y,Y) :- X =< Y, !.
max(X,Y,X).
虽然看上去程序更加简洁, 但此时程序会在 max/3 的三个作用域全部被分别实例化为某些值 (也就是被赋值) 的情况下出错:
1
?- max(114, 514, 114).
此时执行查询, 由于程序无法成功联合第一条规则, 而第二条规则不会对 X, Y 的大小关系作任何检查, 因此我们提出的明显有误的查询语句会得到 true.
但是这不意味着简化第二条规则的尝试完全是徒劳的. 实际上, 这一问题出现的原因只是我们没有让程序在执行变量联合后再执行剪枝. 只需要进行下述的修改, 就可以得到一个既简化了第二条规则又不影响设计功能的程序:
1
2
max(X,Y,Z) :- X =< Y, !, Y = Z.
max(X,Y,X).
需要注意的是, 此处的剪枝谓词不再是安全的, 因为 我们将它从程序中移除后得到的新程序功能不再和原先的保持一致, 它兼具了 影响程序功能 和 优化运行效率 的作用.
在设计程序时, 应尽量避免使用 不安全剪枝 (Red Cuts), 而只将剪枝谓词用于优化程序的运行效率.
3. 回溯谓词
我们下面考虑这个问题: 要表示 “Vincent enjoys burgers”, 我们只需要将这一概括声明为下列的规则语句:
1
enjoys(vincent, X) :- burger(X).
而我们若要引入一条新的规则: “Vincent doesn’t like Big Kahuna burgers”, 也就是 “Vincent enjoys burgers, except Big Kahuna burgers”, 要如何实现这一规则?
在这里, 我们的基本逻辑是: 声明两条规则, 其中第一条规则用于检测给定的变量 X 是否为 Big Kahuna burgers, 而第二条规则单纯检测 X 是否为其他类型的汉堡. 需要注意的是, 若 X 确实为 Big Kahuna burger, 则查询搜索在完成对第一条规则的联合后就应该立刻停止.
在上述两节的学习中我们已经了解了 Prolog 内置的, 用于阻止回溯的 ! (Cut) 谓词, 在这个例子中我们可以利用剪枝谓词提交证明搜索的结果. 而要让程序在尝试满足某个子目标时终止, 就必须确保这个子目标始终无法被满足, 从而强制程序执行回溯.
Prolog 内置的另一个谓词 fail/0 (回溯谓词) 就可以实现这一点. 和 ! 类似, fail 可被视为一个始终 无法得到满足的目标, 因此在任何一轮证明搜索时如果 fail 作为子目标之一, 那么证明搜索就无法继续下去而被迫执行回溯, 也就是说 fail 有 强制程序在当前节点回溯 的作用. 当回溯谓词和剪枝谓词结合时, 我们就可以一并利用它们各自的性质完成对 “特例” 的实现.
继续考虑原来的例子. 在下面一段代码中, 知识库中的第一条规则经过修改后引入了回溯谓词和剪枝谓词. 可见当程序尝试联合第一条规则, 并满足了第一个子目标 big_kahuna_burger(X) 后, 当前对知识库中事实和对知识库中规则的选择会被 ! 作为查询结果提交 (Commit), 此时程序会因为需要满足一个永不能被满足的子目标 fail 而被迫停机, 返回的查询结果就是此前剪枝谓词提交的结果.
1
2
3
4
5
6
7
8
9
10
11
enjoys(vincent,X) :- big_kahuna_burger(X),!,fail.
enjoys(vincent,X) :- burger(X).
burger(X) :- big_mac(X).
burger(X) :- big_kahuna_burger(X).
burger(X) :- whopper(X).
big_mac(a).
big_kahuna_burger(b).
big_mac(c).
whopper(d).
需要注意的是, 上述修改仍然依赖规则的顺序. 若我们将两条规则顺序对换, 程序的功能和行为会相应地发生改变, 第一条规则中的剪枝谓词显然也是 不安全的. 简而言之, 经过上述的修改, 我们得到的 Prolog 程序中两条规则互相依赖, 而且它们的正常执行也是高度依赖于 Prolog 程序执行中的过程式解释性质的.
我们可以进一步将程序定义 “特例” 的核心部分 封装. 在这个例子中, 显然我们所定义的 “特例” 本质上是一种 否定: “Vincent DOES NOT enjoy X if X is a Big Kahuna burger”.
也就是说, 第一条规则中剪枝谓词和回溯谓词的结合实际上表示了某种否定. 我们称这样的结合为 否定为失败, 它是对逻辑否定进行的释义: 公式的否定为真, 当且仅当该公式无法被证明为真:
1
2
neg(Goal) :- Goal, !, fail.
neg(Goal).
显然, neg(Goal) 为真, 当且仅当目标 Goal 不为真.
在将剪枝谓词和回溯谓词的结合封装为否定即失败谓词 neg/1 后, 我们可以将程序简化为:
1
enjoys(vincent, X) :- burger(X), neg(big_kahuna_burger(X)).
也就是说: “Vincent enjoys X if X is a burger and X is not a Big Kahuna burger.”
否定即失败 谓词除了可以简化逻辑表述外, 它被封装为单个谓词的形式令我们无法直接接触 不安全剪枝谓词, 因此减少了在程序设计时出现奇怪错误的几率. Prolog 中直接内置了 否定即失败谓词 : \+. 我们无需自行定义和实现否定即失败谓词, 而可以直接调用它:
1
enjoys(vincent, X) :- burger(X), \+ big_kahuna_burger(X).
需要注意的是, 否定即失败谓词 对程序行为的影响是 和它在规则中的位置有关的. 考虑下面的例子:
1
2
3
4
5
6
7
8
9
10
enjoys(vincent, X) :- burger(X), \+ big_kahuna_burger(X).
burger(X) :- big_mac(X).
burger(X) :- big_kahuna_burger(X).
burger(X) :- whopper(X).
big_mac(a).
big_kahuna_burger(b).
big_mac(c).
whopper(d).
若我们将 \+ big_kahuna_burger(X) 和 burger(X) 调换位置, 程序将始终输出查询结果 no, 因为在替换后执行证明搜索时首先需要被满足的子目标就是 \+ big_kahuna_burger(X), 也就是说要满足 “big_kahuna_burger(X) 不能被满足”, 而对于首次证明搜索, 程序显然是可以从知识库中找到满足 big_kahuna_burger(X) 的事实 big_kahuna_burger(b) 的, 因此 \+ big_kahuna_burger(X) 无法被满足, 从而联合失败, 证明搜索返回结果 no.
总的来说, 否定即失败谓词 并不是单纯的逻辑否定, 我们更需要关注它的过程式描述. 此外, 除非为了提高程序的运行效率, 在大多数情况下使用该谓词都比在程序中应用不安全剪枝更合适.
