语义树
本章介绍 语义树, 它是另一种可用于可满足性检查和生成谓词公式模型的工具. 给定谓词公式的语义树的生成规则基于对逻辑联结词运算表的分析. 通过应用这些生成规则, 我们就可以得到给定谓词公式的 所有模型.
我们首先对 语义树 进行定义, 随后讨论语义树逻辑演算的健全性和完备性. 在第三节中, 我们将给出一个通过捕捉从分支中被删除的公式并使用名为 可逆性 的证明理论论证来确立公式的可满足性的语义树运算.
7.1 语义树 (Semantic Tableaux)
首先考虑一个检查谓词公式
\[\neg (q \vee p \rightarrow p \vee q)\]可满足性的例子.
首先考虑逻辑联结词 $\neg$, 显然可知若该公式存在一个解释 $I$, 则该解释必使
\[(q \vee p \rightarrow p \vee q)\]为真. 进一步地考虑联结词 $\rightarrow$, 可知 $I$ 必使
\[(q \vee p) = 1, ~~ (p \vee q)=0.\]最后, 同时考虑两个 $\vee$, 我们可得该解释必须同时满足
\[p=0, ~~ q=0; ~~ q=1 ~\text{or} ~ p=1.\]由于这样的赋值是互相矛盾的, 显然可知该谓词公式不存在任何模型, 因此它是不可满足的.
在上述的过程中, 我们基于联结词对子公式进行的分别检查流程大致可以用下图表示:
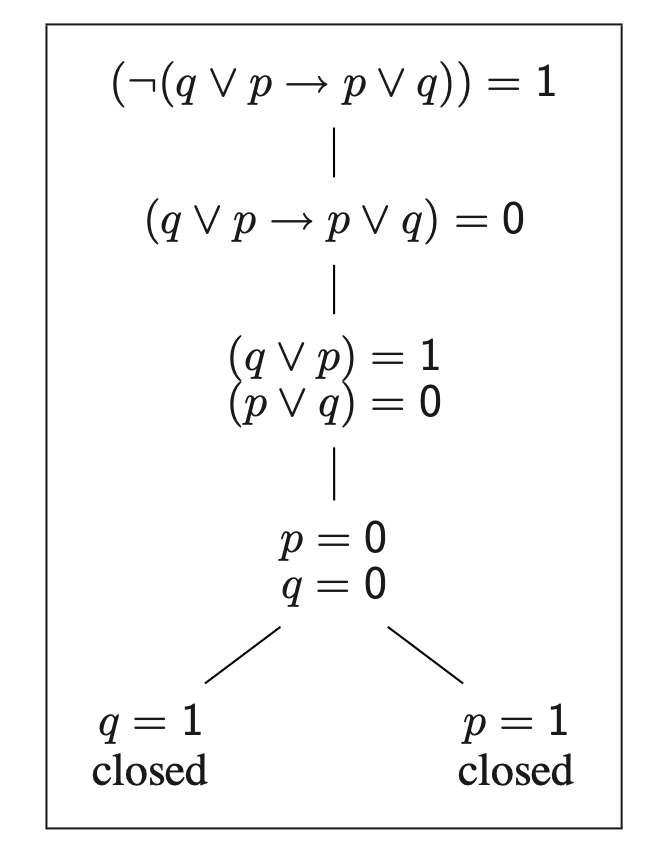
其中决策树的节点为所需要满足的子公式赋值, 而每一个分支都代表一种可选的赋值方式.
本质上, 在尝试构造该公式的模型时, 我们采取的策略是基于逻辑联结词的操作表得出 “为了使包含该联结词的谓词公式被解释为特定值, 该公式内位于该链接词不同作用域内的子式需要满足的条件”, 并根据这些在拆解过程中逐步被简化的条件最终依次得出为使原公式被解释为真, 各个变量所需要被赋予的值.
由于我们在每一次拆分中都会将所有可行的赋值方式和解释方式考虑在内, 通过这种方法得出的全体解释就是原谓词公式的全部模型.
将我们的检索过程可视化的搜索树被称为 语义树 (tableaux). 语义树的分支分为两种类型: 开 和 闭:
定义 7.1.1 (开分支和闭分支) 若语义树中的任何一个分支可被确认为无法得到原公式的一个模型, 则这一分支就被称为 闭分支, 反之则称为 开分支.
构造语义树可被视为一个单人决策过程 (One-Player Game). 这样的决策过程包含一系列决策: 在每一步中, 决策者都从可选的规则和策略中选择一个, 而每一次决策都会影响当前局势的配置 (Configuration).
对于语义树问题而言, 将它视为决策问题时它的配置就是一张语义表 tableau. 在为给定的一个谓词公式 $\alpha$ 构造语义表时, 首先构造一个被标记为 $\alpha$ 的单节点, 注意此时我们的语义表中有且只有一条分支, 且该分支显然应该被同时声明为 开分支.
随后, 决策者可执行的操作被大致分为以下的两类:
i. 在当前的语义表中选择某个开分支 $B$, 并在该分支上选择一个 有符号公式 $\alpha$, 且该公式需满足 $\alpha$ 不为有符号原子 (也就是说要选择一个尚未被赋值的谓词原子并且同时考虑某个在该分支中包含该原子的子式).
ii. 使用下列的规则扩展语义表:
我们下面介绍语义表的扩展规则. 这些规则或在分支 $B$ 下增加新节点, 或在当前分支处展开新分支. 规定 $B$ 表示分支, 而 $\beta$ 表示将要作为叶子节点添加到 (相对而言的!) 根结点 $B$ 下的谓词公式, 或包含公式 $\beta$ 的叶子结点. 则我们有下列规则:
规则 7.1.1 (分支扩展规则)
\[(A_1 \leftrightarrow A_2)=1,\]
若 $\alpha$ 形为
\[(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=0,\]则将 $\beta$ 作为 $n$ 个子节点 挂在 $B$ 下, 分别为
\[A_1=0, A_2=0, \cdots, A_n=0.\]若 $\alpha$ 形为
\[(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=1,\]则将 $\beta$ 作为一个 单独子节点 挂在 $B$ 下, 包含公式
\[A_1=1, A_2=1, \cdots, A_n=1.\]若 $\alpha$ 形为
\[(A_1 \vee A_2 \vee \cdots \vee A_n)=0,\]则将 $\beta$ 作为一个 单独子节点 挂在 $B$ 下, 包含公式
\[A_1=0, A_2=0, \cdots, A_n=0.\]若 $\alpha$ 形为
\[(A_1 \vee A_2 \vee \cdots \vee A_n)=1,\]则将 $\beta$ 作为 $n$ 个子节点 挂在 $B$ 下, 分别为
\[A_1=1, A_2=1, \cdots, A_n=1.\]若 $\alpha$ 形为
\[(A_1 \rightarrow A_2)=0,\]则将 $\beta$ 作为一个 单独子节点 挂在 $B$ 下, 包含公式
\[A_1=1, A_2=0.\]若 $\alpha$ 形为
\[(A_1 \rightarrow A_2)=1,\]则将 $\beta$ 作为 $2$ 个子节点 挂在 $B$ 下, 分别为
\[A_1=0, A_2=1.\]若 $\alpha$ 形为
\[(\neg A_1)=0,\]则将 $\beta$ 作为一个 单独子节点 挂在 $B$ 下, 包含公式
\[A_1=1.\]若 $\alpha$ 形为
\[(\neg A_1)=1,\]则将 $\beta$ 作为一个 单独子节点 挂在 $B$ 下, 包含公式
\[A_1=0.\]若 $\alpha$ 形为
\[(A_1 \leftrightarrow A_2)=0,\]则将 $\beta$ 作为 $2$ 个子节点 挂在 $B$ 下, 分别为
\[A_1=0, A_2=1\]和
\[A_1=1, A_2=0.\]若 $\alpha$ 形为
则将 $\beta$ 作为 $2$ 个子节点 挂在 $B$ 下, 分别为
\[A_1=0, A_2=0\]和
\[A_1=1, A_2=1.\]
上述规则可被总结为下图, 其中有符号谓词公式 $\alpha$ 位于符号 $\rightsquigarrow$ 左侧, 叶子结点 $\beta$ 的子节点位于符号右侧, 若有多个子节点的话则用 $\vert$ 分隔.
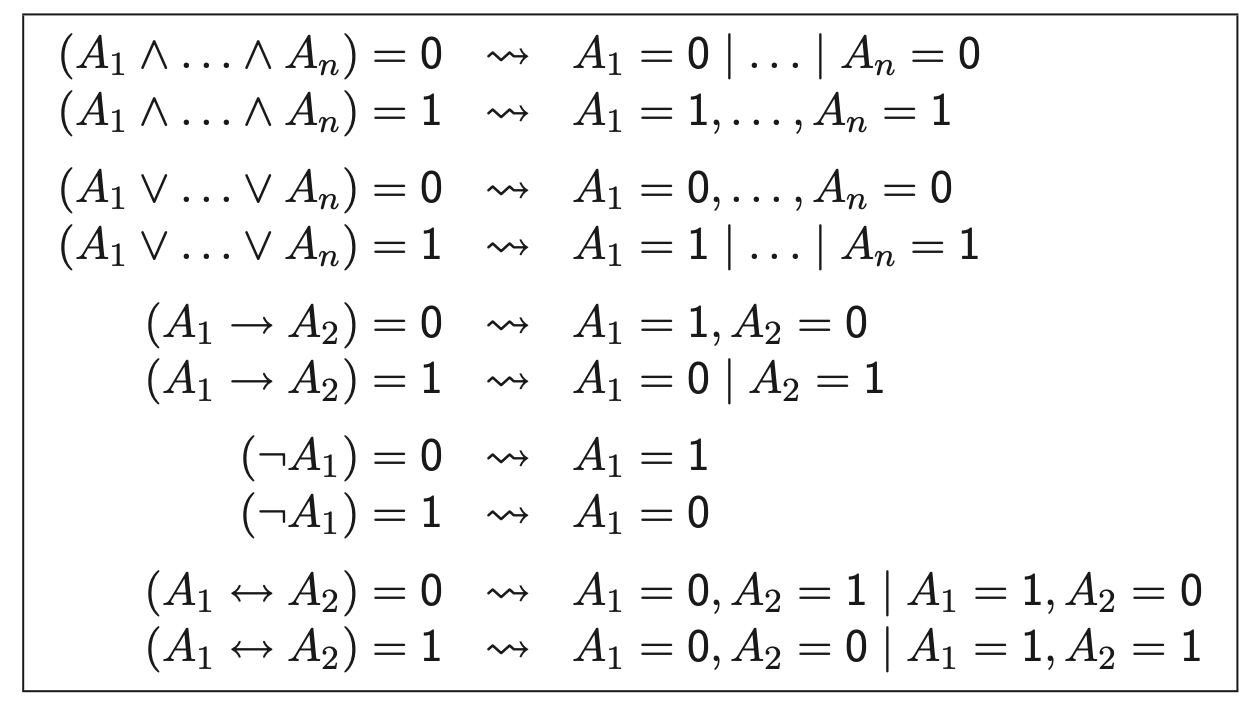
与之相对的, 我们还有两条 分支闭合规则:
规则 7.1.2 (分支闭合规则)
i. 若语义表的某个分支同时包含某个有符号谓词原子 $p$ 的一对值
\[p=0, ~~ p=1\]则该分支被标记为 闭合分支.
ii. 若语义表的某个分支包含任一赋值
\[\top = 0\]或
\[\perp=1\]则该分支也被标记为 闭合分支.
显然. 基于分支扩展和分支闭合规则生成的语义表会随着决策着做出选择的变化而变化, 因而它是 非确定性 的.
此外, 为了确保决策一定会终止, 我们必须 禁止对分支上已选择过的公式进行二次选择. 此外, 不可选择已经被标记为闭合分支的分支.
不难看出, 在引入上述规则后任何博弈过程都是有限的, 因为在每次决策过程执行后, 在原节点下加入的新子式都比原式小. 因此, 对于任何决策, 我们都有下述的两种可能:
- 由于所有分支都闭合, 不再存在任何可能的新决策.
- 存在一个开分支, 但该分支上的任何有符号公式都已经被选择过, 因而不可再进行任何选择.
我们称第一种情况下 给定的原公式是不可满足的, 而对于第二种情况下原公式是 具备可满足性 的.
下面我们说明, 在第二种情况下我们可以构造出一个原公式的模型:
不妨假设一次决策终止且我们得到的语义表中 包含一个开分支. 设 $B$ 为这个开分支中的全部有符号公式, 考虑对于任意布尔变量 $p$, 满足下述要求的解释 $I$:
\[I(p) \overset{\text{def}}{=} \begin{cases} 0~~~ \text{if} ~~ (p=0) \in B \\ 1 ~~~ \text{if} ~~ (p=1) \in B\end{cases}\]而若某个布尔变量 $p$ 在该分支中没有出现 (也就是说它的可行取值没有被限定), 则我们可以在构造解释 $I$ 时对它取任意值. 不难证明 (见下节), 这样构造出的解释 $I$ 不仅是位于语法树根部的谓词公式的模型, 还是分支上每一个有符号公式的模型.
7.2 可靠性和完备性
逻辑往往使用合适的概念模型 (Notion of Model), 以语义 (Semantic) 的方式定义. 语义树的 逻辑演算 或 解析演算 则是通过 证明 或 逻辑推断 的概念定义的.
为了确认构造的模型理论语义 (Model-Theoretic Notions) 和证明理论语义 (Proof-Theoretic Notions) 具一致性, 我们需要证明它的 可靠性 (Soundness) 和 完备性 (Completeness).
直观地说, 可靠性 意味着任何在该算法下有证明的谓词公式都是语义上合法的 (谓词公式要么为有效的, 要么为可满足的). 而 完备性 意味着任何有效或可满足的公式在该算法下都有对应的证明.
在本章中, 我们将证明语义树法是 可靠和完备 的. 也就是说:
- 有符号谓词公式 $\alpha$ 是可满足的, 当且仅当每一个终止的决策都有一个开分支.
- 有符号谓词公式 $\alpha$ 是可满足的, 当且仅当每一个终止的决策的分支都是闭的.
假设每一轮决策 (game) 都从一个记为 $\gamma$ 的初始有符号公式开始. 一般地, 我们会将 语义表的某个分支 和 位于该分支上的全部有符号谓词公式组成的集合 相关联. 举例而言, 若语义表的某个分支上全部有符号谓词公式组成的集合是可满足的, 我们则称该分支为 可满足的.
下面我们将证明两个命题:
- 若某个语义表的全部分支都是闭分支, 则 $\gamma$ 为不可满足的.
- 若在决策过程终止后语义表中仍存在一开分支, 则我们可从这一分支中提取出 $\gamma$ 的一个模型.
引理 7.2.1
记解释 $I$, 记 $T$ 为通过数轮决策后所得到的语义表. 则 $I$ 为 $\gamma$ 的一个模型, 当且仅当 $I$ 为 $T$ 的任一分支的模型.
证明
我们对决策的轮数应用数学归纳法.
首先考虑基础情形. 在进行了 $0$ 轮决策后, $T$ 仍是原来的语义表, 因此结论显然成立.
其次假设原结论对这样生成的某个 $T$ 亦成立, 并且对一切从 $T$ 通过应用任意一条分支扩展规则而得到的新表 $T’$也成立. 不妨假设 $B$ 为从 $T$ 中选定的一条分支, $\alpha$ 为在该分支中选定的一个谓词公式.
下面只考虑 $\alpha$ 形如 $(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=0$ 的情形:
设 $B, B_1, \cdots, B_m$ 为 $T$ 的所有分支, 则 $T’$ 的分支为 $B_1, \cdots, B_m$: $B \cup {A_1 = 0}, B \cup {A_2 = 0}, \cdots, B \cup {A_n = 0}$. 由归纳假设: $I$ 为 $\gamma$ 的模型, 当且仅当 $I$ 为 $T’$ 某分支的模型.
由于 $I$ 为 $B_1, \cdots, B_m$ 模型的情形显然, 我们下面考虑 $I$ 不为 $B_1, \cdots, B_m$ 的模型的情形.
必要性: 假设 $I$ 为 $B$ 的某个模型, 则 $I$ 为 $(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=0$ 的某个模型. 故我们可以立刻得知, 对于某个 $i \in [n]$, $I$ 必为 $A_i = 0$ 的模型. 由于该有符号谓词公式位于分支 $B$ 上, 且 $I$ 同时为 $A_i = 0$ 的模型, 故它必为 $B \cup {A_i=0}$ 的模型. $\blacksquare$
充分性: 显然从 $I$ 为 $B \cup {A_i=0} ~~ \text{for some}~i \in [n]$ 可知, $I$ 显然是 $B$ 的一个模型. $\blacksquare$
我们下面引入 平凡地不可接受的 的概念:
定义 7.2.1 (平凡地不可接受的)
若某个有一系列由符号谓词公式组成的集合中包含:
- 一对原子 $p$ 的相反赋值 $p=1, ~ p=0$
- 至少包含 $\top = 0$ 或 $\perp = 1$ 其中一个 则称该集合是 平凡地不可接受的.
显然, 任何 平凡地不可接受的 有符号谓词公式集合都是不可接受的. 进一步地我们有下列引理:
引理 7.2.2
一个语义表的分支为 闭分支, 当且仅当它为 平凡地不可接受的.
引理 7.2.3
记 $T$ 为公式 $\gamma$ 的语义表. 若 $T$ 中所有分支都为闭分支, 则 $\gamma$ 为不可接受的.
证明
不妨假设 $\gamma$ 存在一个解释 $I$. 则由 引理7.2.1, $I$ 亦为 $T$ 中任一分支的模型. 由定义知 $T$ 中任何闭合分支均为 平凡地不可接受的, 因此不可能被任何解释满足, 不存在模型, 和证明开头的假设矛盾, 因此假设不成立, 原引理为真. $\blacksquare$
通过上面的叙述, 我们已经证明了若某个语义表的全部分支都是闭分支, 则 $\gamma$ 为不可满足的. 下面我们说明, 在决策过程终止后语义表中仍存在的开分支的模型存在. 我们首先引入 饱和集 的概念:
定义 7.2.2 (饱和集)
称由有符号谓词公式组成的集合 $S$ 为 饱和的 (
Saturated), 若:
若 $S$ 包含一个有符号公式 $(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=0$, 则 $S$ 同时至少包含有符号公式 $A_1=0, A_2=0, \cdots, A_n=0$ 中的至少一个.
若 $S$ 包含一个有符号公式 $(A_1 \wedge A_2 \wedge \cdots \wedge A_n)=1$, 则 $S$ 同时至少包含有符号公式 $A_1=1, A_2=1, \cdots, A_n=1$ 中的至少一个.
若 $S$ 包含一个有符号公式 $(A_1 \vee A_2 \vee \cdots \vee A_n)=0$, 则 $S$ 同时包含有符号公式 $A_1=0, A_2=0, \cdots, A_n=0$.
若 $S$ 包含一个有符号公式 $(A_1 \vee A_2 \vee \cdots \vee A_n)=1$, 则 $S$ 同时包含有符号公式 $A_1=1, A_2=1, \cdots, A_n=1$.
若 $S$ 包含一个有符号公式 $(A_! \rightarrow A_2)=0$, 则 $S$ 同时包含有符号公式 $A_1=0, A_2=0$.
若 $S$ 包含一个有符号公式 $(A_! \rightarrow A_2)=0$, 则 $S$ 或包含有符号公式 $A_1=0$, 或包含 $A_2=1$.
若 $S$ 包含一个有符号公式 $\neg A_1 = 0$, 则 $S$ 同时包含 $A_1 = 1$.
若 $S$ 包含一个有符号公式 $\neg A_1 = 1$, 则 $S$ 同时包含 $A_1 = 0$.
若 $S$ 包含一个有符号公式 $A_1 \leftrightarrow A_2=0$, 则 $S$ 同时包含 $A_1 = 0, ~ A_2=1$, 或 $A_1 = 1, ~ A_2=0$.
若 $S$ 包含一个有符号公式 $A_1 \leftrightarrow A_2=1$, 则 $S$ 同时包含 $A_1 = 0, ~ A_2=0$, 或 $A_1 = 1, ~ A_2=1$.
显然, 若一个集合为饱和集, 它必包含了能够使得该集合中全部有符号公式都为其预设值 (如考虑公式 $\neg A_1=1$, 则其预设值就是 $1$) 的的变量赋值. 因此有下列结果:
引理 7.2.4
记对 $\gamma$ 的语义树决策在语义表 $T$ 终止. 则 $\gamma$ 中的任何 开分支 都是饱和集.
引理 7.2.5
记 $B$ 为由一系列谓词公式组成的饱和集. 则 $B$ 为可满足的, 当且仅当它不为 平凡地不可接受 的.
证明
显然 $B$ 为不可接受的, 若它是平凡地不可接受的. 下面考虑 $B$ 不为平凡地不可接受的情形, 则要证我们可以生成 $B$ 的某个模型.
下面构造满足如下条件的解释 $I$:
\[I(p) \overset{\text{def}}{=} \begin{cases} 0~~~ \text{if} ~~ (p=0) \in B \\ 1 ~~~ \text{if} ~~ (p=1) \in B\end{cases}\]显然 $I$ 良好地定义了 $B$ 中每一个原子的值, 不会出现对某个原子 $p$, 解释 $p=0$ 和 $p=1$ 同时在 $I$ 中出现的情形. 下证 $I$ 为 $B$ 中任一有符号公式 $\alpha$ 的模型:
我们可对 $\alpha$ 的大小应用数学归纳法, 并不难看出该结论成立. 此处不再赘述具体的证明过程.
在完成了上述的全部铺垫后, 我们下面可以给出对语义表方法可靠性和完备性的证明:
定理 7.2.1 (可靠性和完备性)
设 $T$ 为某个以有符号公式 $\alpha$ 为起点的, 终止了的决策生成的语义表. 则 $\gamma$ 为不可满足的, 当且仅当语义表 $T$ 中所有分支均为闭分支.
证明
若 $T$ 中全部分支均为闭分支, 则由
引理 7.2.3, $\gamma$ 为不可接受的. 下面证明原陈述的反面: 若 $T$ 中存在开分支, 则 $\gamma$ 必为可满足的:若存在某个开分支 $B$, 则由
引理 7.2.4, $B$ 必为饱和集, 同时 $B$ 不为平凡地不可接受的. 因此又由引理 7.2.5, 可知 $B$ 为可接受的, 进而 $B$ 必有一个模型 $I$.由于任何分支必包含根结点 $\gamma$, 因此 $\gamma \in B$, 由此可知 $I$ 同时也是 $\gamma$ 的模型, 由此 $\gamma$ 为可满足的. $\blacksquare$
值得注意的是, 和语义树的规模不同, 该定理成立与否和我们在执行决策时对分支的选择 无关.
下面讨论一些 可靠性和完备性定理 的应用:
推论 7.2.1
下列陈述成立:
- 谓词公式 $F$ 是可满足的, 当且仅当对于任意有符号谓词公式 $F=1$ 的终止的语义表都具一个开分支.
- 谓词公式 $F$ 是有效 (
valid)的, 当且仅当对于任意有符号谓词公式 $F=0$ 的终止的语义表的分支都是闭分支.- 谓词公式 $F_1, F_2$ 为等价的, 当且仅当任意对有符号谓词公式 $(F_1 \leftrightarrow F_2) = 0$ 的终止的语义表的分支都是闭分支.
7.3 语义树的另一种解释法
在上面的数节中我们介绍了将语义树字面意义地视为树的解释法. 这一解释法无法正确表达 “我们不能重复地在同一分支上选择曾经被选择过的谓词公式” 这一规则, (我们显然不能删除树的某个节点, 因为其副作用是该节点的所有子节点会被一并删除) 并且我们还需要建立截然不同的 分支扩展规则 和 分支闭合规则.
为了规避这一问题, 下面引入对语义树的另一种解释法: 我们会将其视为 一系列由分支组成的集合.
定义 7.3.1 (分支和语义表)
称 分支 为非空的, 有一系列有符号谓词公式组成的集合, 语义表 为由一系列分支
\[\{B_1, \cdots, B_n\}\]组成的有限集合, 记为
\[B_1 \vert \cdots \vert B_n.\]$n=0$ 时, 称其为 空语义表, 记为 $\boxplus$. 称解释 $I$ 为 语义表 $T$ 的一个模型, 若 $I$ 为该表中 至少一个分支 的模型.
注:
- 空语义表不存在任何模型.
- 若某个语义表只包含一条分支, 则该表示可满足的, 当且仅当它所包含的唯一分支是可满足的.
下面我们考虑谓词逻辑下的语义表运算:
定义 7.3.2 (语义表运算)
定义谓词逻辑下的语义表运算包含下列的推断规则:
\[B \cup S_1, ~ B \cup S_2, \cdots, B\cup S_m.\]
分支扩充规则.
\[\alpha \rightsquigarrow S_1 \vert \dots S_m\]
考虑在第一节中介绍的规则 7.1.1. 对于其中任意一条规则, 若它形如且语义表 $T$ 包含分支 $B$, 分支 $B$ 中的谓词公式 $\alpha$ 包含 $\alpha$, 则将 $T$ 中该分支 $B$ 替代为 $m$ 个新分支
分支闭合规则
\[\top = 0, ~ \perp = 1\]
若某分支包含有符号谓词公式中的至少一个或一对互相矛盾的谓词原子取值
\[p=0, ~~ p=1\]则可从语义表中删除这条分支.
对应的, 我们可以将上述的两个规则分别表示为下列的推断法则:

注意, 在 分支扩充规则 中, $B$ 中原先的有符号谓词公式 $\alpha$ 实际上是被 删除 (或替代)的. 在 分支闭合规则 中, 被 “闭合” 的规则实际上也是被 删除 的.
引理 7.3.1
令 $T$ 为某个不可应用任何一条推断法则的语义表. 则有:
- 该表中只包含有符号原子和有符号公式 $\top = 0, ~ \perp = 1$.
- 表中不存在互相矛盾的谓词原子取值.
- 表中的每一条分支都是可满足的.
- 该表为可满足的, 当且仅当该表非空.
我们已经将 分支扩充规则 和 分支闭合规则 表示为两条推断法则 (Inferences). 下面我们引入推断法则 可逆性 的定义, 并利用它直观地证明语义表运算的可靠性和完备性.
定义 7.3.3 (可逆的)
若某个 推断规则 的结论 (
Conclusion) 是可满足的, 当且仅当它的 所有 前提 (Premise) 是可满足的. 则称其为 可逆的.若某个 推断 的的结论 (
Conclusion) 是可满足的, 当且仅当它的 某个 前提 (Premise) 是可满足的. 则称其为 可逆的.
需要注意的是: 语义表推断规则系统中的两条推断规则都有相同的结构: 它们都 只有一条前提, 一条结论.
引理 7.3.2
语义表运算中的每条推断都是可逆的.
定理 7.3.1 (可靠性和完备性)
记 $\gamma$ 为有符号公式, $T$ 为任一语义表, 满足:
- 存在一个从 $\gamma$ 到 $T$ 的推导 (
Derivation).- 任何推断规则都不可应用于 $T$ 上.
则 $\gamma$ 为不可满足的, 当且仅当 $T = \boxplus$.
