可满足性与随机化

在本章中, 我们将继续讨论可满足性的检验问题和随机化问题.

首先我们将讨论如何生成随机化的可满足性问题, 随后我们将说明, 随机生成的可满足性问题集中体现出 “急剧相变” (Sharp-Phase Transition) 的特点: 在一个很小的范围区间内, 可满足性问题就会突然转变为不可满足性问题. 最后, 我们简要说明随机生成的可满足性问题对现存的可满足性检查算法的困难性. 随机化不但会生成极为复杂的可满足性问题, 也能帮助我们求解他们. 我们随后会介绍一系列基于随机生成解释的, 用于检测谓词公式可满足性的随机化算法.

6.1 随机生成的 $\text{SAT}$ 问题

首先回顾 子句 的定义: 子句本质上是一系列文字的析取. 为了随机生成一个由一系列子句组成的集合, 我们需要限制子句的结构并控制文字可选择的范围, 也就是:

1. 确定集合中 要生成的子句的个数.
2. 限制 组成子句的文字的可选范围.
3. 确定 每个子句由多少个文字组成.

我们分别将这三个参数定义为 $m$, $n$ 和 $k$. 显然, 为了确保文字的对称性, $n$ 应当是某个 偶数. 对于给定的 $2n$, 我们可以从 $p_1, p_2, \cdots, p_n, \neg p_1, \neg p_2, \cdots, \neg p_n$ 共 $2n$ 个不同的文字中选择, 因而每个文字被选择的概率均为 $\frac{1}{2n}$.

下面我们考虑在 ${p_1, p_2, \cdots, p_n, \neg p_1, \neg p_2, \cdots, \neg p_n}$ 中任意挑选文字, 随机生成 $m$ 个 $k-$ 子句并组成一个子句集合, 讨论该集合的可满足性, 求生成的集合具备不可满足性的概率.

在 $m=1$ 时, 显然生成的集合只包含一个子句, 它自然是可满足的.

在 $m=2$ 时, 如果这样的集合是不可满足的, 显然它的两个元素必须互斥, 也就是说它们必然形如 $p_{i1} \vee p_{i2} \cdots \vee p_{ik}$ 和 $\neg p_{i1} \vee \neg p_{i2} \cdots \vee \neg p_{ik}$. 显然生成这样的集合的概率为:

显然这个数额对于任何 $n$ 和 $k$ 而言都是相当小的, 这意味着在这个限制条件下我们不太可能构造出具备不可满足的集合, 也就是说对于 $m$ 很小的情形, 这个问题是 乏约束 (under-constrained) 的. 然而, 若我们考虑 $m$ 足够大的情形时, 这个问题会变成一个 过约束 (over-constrained) 问题, 因为此时若我们还希望能够找到一个具备可满足性的集合, 就需要同时满足比原来多得多的约束条件, 因此可行解的求解难度直线上升.

我们考虑这样的坐标系: 横轴为 生成子句的个数 $m$ 和文字的可选范围 $n$ 的比值 $\frac{m}{n}$, 纵轴为该比例对应的, 基于这个配置生成的子句集合 具不可满足性 的概率. 对于每一个 $n$, 实际上都存在一个交叉点 (crossover point), 在 $\frac{m}{n}$ 移过该点时对应的概率恰好完成从 $< \frac{1}{2}$ 到 $> \frac{1}{2}$ 的跨越. 而概率关于比值 $\frac{m}{n}$ 的分布非常类似于 Sigmoid 函数: 概率值在交叉点附近会出现从极度趋近于 $0$ 到极度趋近于 $1$ 的剧烈转变.

从此处开始若无特殊说明, 我们只考虑 $k=3$ 的情况, 也就是只考虑 $3-\text{SAT}$ 问题. 下面给出对在上一段中介绍的一些概念的严格定义:

定义 6.1.1 (比值)

称 比值 (Ratio) 为 生成子句的个数 $m$ 和文字的可选范围 $n$ 的比 $\frac{m}{n}$, 记为 $r$.

注:

此处我们记 “由 $r \cdot n = m$ 个随机生成的, 由范围 ${p_1, p_2, \cdots, p_n}$ 内可选的文字所组成的 $3-$ 子句随机生成的子句集合具不可满足性” 的概率为 $\pi(r, n)$.

定义 6.1.2 (交叉点)

称满足下列条件的值 $r$ 为 交叉点 (Crossover Point):

1. 对任意 $r’ < r$, 有 $\pi(r’, n) < 0.5$.
2. 对任意 $r’ > r$, 有 $\pi(r, n) \geqslant 0.5$.

6.2 急剧相变

下面的例子明确揭示了 急剧相变 的基本特征: 在一个以 交叉点 为中心的极小区间内, 函数值从趋近于 $0$ 到 趋近于 $1$ 急剧变动.

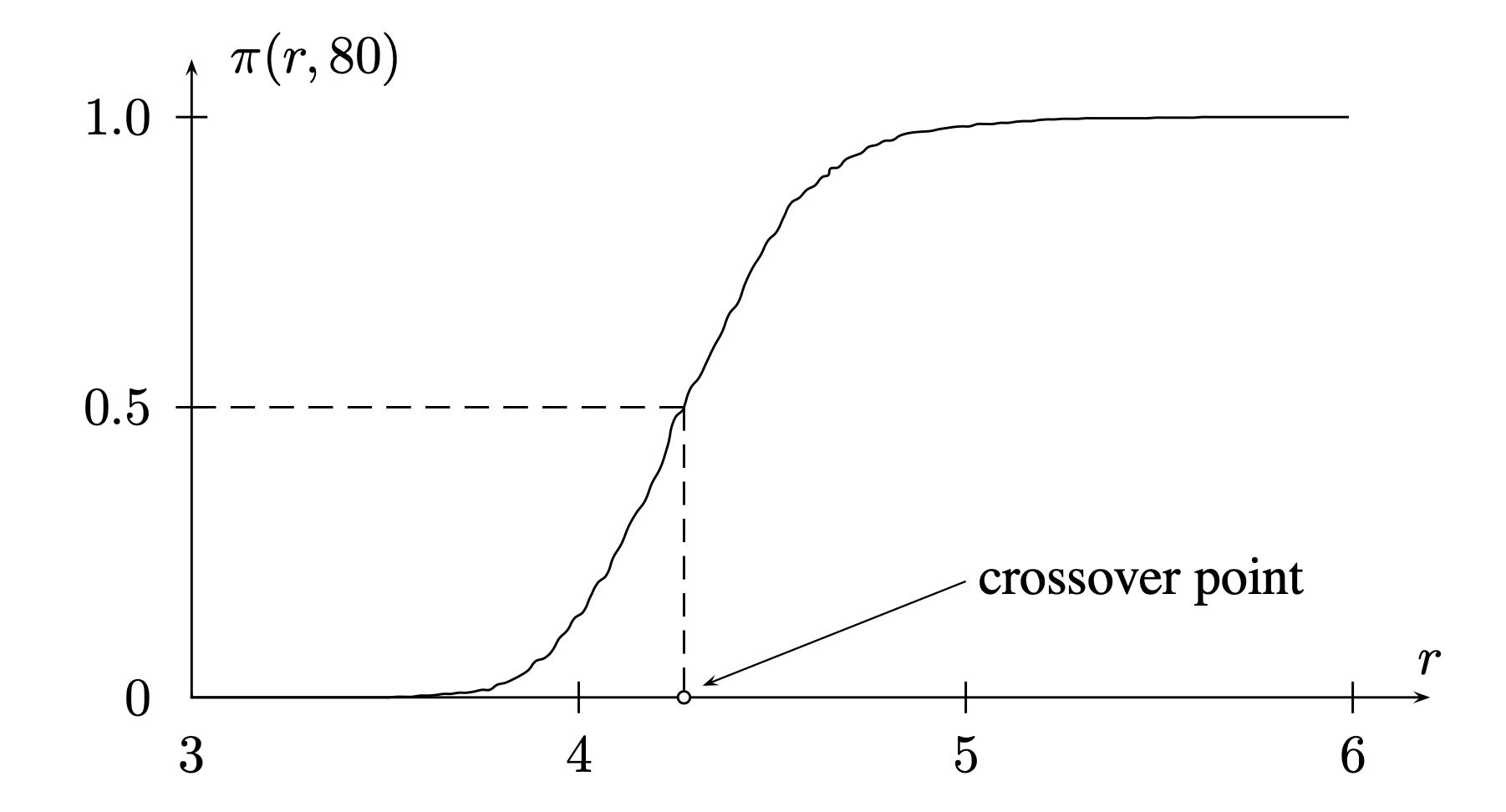
为了形式化地定义 “很接近于”, 我们选取一个很小的整数 $\epsilon$, 称其为 几乎为 $0$, 并称 $1-\epsilon$ 为 几乎为 $1$.

定义 6.2.1 (窗口)

考虑满足条件 $0 < \epsilon < 0.5$ 的实数 $\epsilon$. 称 $\epsilon-$ 窗口 为由所有满足 $\epsilon \leqslant \pi(r, n) \leqslant 1-\epsilon$ 的比例 $r$ 组成的集合.

本质上, “$\epsilon-$ 窗口” 就是概率值从 “几乎为 $0$” 转变为 “几乎为 $1$” 的区域. 若这个窗口非空, 则它必包含 交叉点.

我们同时记窗口的宽度为 $\text{window}(\epsilon, n)$. 关于 窗口的宽度, 我们有下述结论:

推论 6.2.1

对随机生成的 $3-\text{SAT}$ 问题, 任何 $\epsilon$ 均满足:

\[\lim_{n \rightarrow \infty} (\frac{\text{window}(\epsilon, n)}{\text{crossover}(n)}) = 0.\]

也就是说, $\epsilon-$ 窗口的宽度会随着 $n$ 的递增而逐渐收缩, 直到最终退化为交叉点, 而函数本身从一个类 Sigmoid 函数退化为一个单纯的阶跃函数.这就是所谓的 急剧相变.

6.3 面向 SAT 问题的随机化算法

我们可以通过引入 随机性 构造一个可用于检验 SAT 问题是否具备不可满足性的算法. 这样的随机算法可以用于解决更复杂的, 那些常规算法无法解决的问题, 但随机算法 是不完备的, 它只能部分地解决我们的问题: 如果给定的 SAT 问题是可满足的, 它有 一定的几率 给出这个问题的一个解释, 从而得证该问题具可满足性; 而若该问题实际上是不可满足的, 它由于无法在多项式时间内遍历地检测该问题的所有解释并说明这些解释都不能满足它, 因此算法 并不能说明该问题的不可满足性.

本质上, 这样的 不完备 算法依赖 随机生成 的解释, 若能找到满足问题的特例才能得出确定的结果, 反之则并不能给出肯定的答复.

所有的 $\text{NP-Complete}$ 问题都具备类似的特征. 进一步地, 任何 $\text{NP}$ 都有多项式长度的见证.

定义 6.3.1 (见证)

我们称某个决策问题的实例 $i$ 的某个 见证 (Witness) 为一个字符串 $s$, 使得给定实例 - 见证对 $(s, i)$, 我们可以在多项式时间内检测在 $s$ 的基础上实例 $i$ 是否为真.

显然, 如果一个问题有足够短的见证, 我们就可以通过随机地猜测它的见证, 通过检测这些见证是否真的使实例为真. 若能找到一个这样的见证, 我们就可以终止流程并对问题的真伪给出肯定的答复, 但如果我们找不到见证的话, 我们并不能得出任何新的事实. 通过这样的逻辑, 我们就得到了 不完全 的算法.

下面我们将介绍数个用于检测谓词可满足性的不完备算法. 我们首先来看一个最直观的随机算法:

1. Toy Model

算法 6.3.1 (CHAOS)

1
2
3
4
5
6
7
8
9
10
11
procedure CHAOS(S)
input: set of clauses S
output: interpretation I such that I ⊧ S or don't know
parameters: positive integer MAX-TRIES

begin 
    repeat MAX-TRIES times
        I := random interpretation
        if I ⊧ S then return I
    return don't know
end

CHAOS 算法通过检测给定的子句集合是否能被随机生成的有限个解释中任意一个满足来判断能否确定该子句集合具备可满足性. 解释的生成方式是纯粹随机的, 不受任何其他因素的影响, 因而性能有限.

我们下面介绍一系列更复杂的随机化算法:

2. 局部搜索 (GSAT)

局部搜索过程基本上基于一个假设: 通过不断修改解释使得该解释无法满足的子句数量最小化, 我们就更有可能最终得到一个能够满足整个子句集合的解释. 这样的流程一般被称为 GSAT.

对于给定的, 无法完全满足子句集合 $S$ 的解释 $I$, 我们尝试 翻转 $I$ 中的一个变量, 旨在让新的解释 $I$ 能满足集合中子句的数量最大化. 若对不同变量的翻转得到的可满足子句数相同, 我们就从这些同等最优的结果中随机挑选一个.

这一步骤的伪代码化描述如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
procedure GSAT (S)
input: set of clauses S
output: interpretation I such that I ⊧ S or don’t know 
parameters: positive integers MAX-TRIES, MAX-FLIPS 

begin
    repeat MAX-TRIES times
        I := random interpretation 
        if I ⊧ S then return I 
        repeat MAX-FLIPS times
            p := a variable such that flip(I, p) satisfies
                    the maximal number of clauses in S
            I = flip(I,p)
            if I ⊧ S then return I 
    return don’t know
end

需要注意的是, 对于局部搜索过程而言, “局部搜索选择了错误的方向, 并最终只能得到局部最优而非全局最优” 的概率是 不能被排除的. GSAT 避免局部最优的方法很激进: 若在某一次尝试中, 基于当前解释多次翻转变量得到的新结果性能一致, 且翻转次数超过了预设的最大限制 `$\text{MAX-FLIPS}$ 时, 算法会认定该解陷入了局部最优而直接舍弃该解重新随机生成新解.

3. 随机游走 (GSAT with random walks)

和机器学习中引入随机性优化梯度下降法从而得到随机梯度下降法的基本逻辑相同, 我们也可以通过进一步地在 GSAT 中引入随机性降低它在寻找最优解的过程中陷入局部最优的概率.

和局部搜索不同, 随机游走在每一步中找到最优解释后还会以概率 $\pi$ 翻转解释中的变量 $p$. 需要注意的是, 变量 $p$ 并不是随机选择的, 而要满足一定的条件才会对避免陷入局部最优起到正面效果. 一般地, 这样的 $p$ 应该在至少一条不可被当前解释满足的子句中出现.

随机游走的伪代码描述如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
procedure GSAT (S)
input: set of clauses S
output: interpretation I such that I ⊧ S or don’t know 
parameters: positive integers MAX-TRIES, MAX-FLIPS
            real number 0 ≤ μ ≤ 1 (probability of a sideways move),
begin
    repeat MAX-TRIES times
        I := random interpretation 
        if I ⊧ S then return I 
        repeat MAX-FLIPS times
            with probability μ
                p := a variable such that flip(I,p) satisfies...
                     ...the maximal number of clauses in S with...
                     ...probability 1 − μ
                randomly choose p among variables occurring...
                ...in clauses false in I 
            I = flip(I,p)
            if I ⊧ S then return I
    return don’t know 
end               

• Previous
  逻辑学探幽 Part5
• Next
  逻辑学探幽 Part7