DPLL
本章讨论的主要对象是最常见的可满足性检验方法: DPLL,其名称来源自它的发明者. 该方法所检验的对象是 合取范式 或 由一系列子句构成的集合.
我们首先引入 子句 与 合取范式 的概念, 并在第二节中回顾对于谓词公式的合取范式求解算法. 我们会在第三章中讨论合取范式求解算法的时间复杂度问题, 并给出一种基于定义上的将谓词公式转换为由一系列子句构成的集合的方法.
我们会在第四节中介绍一个关于子句的可满足性的特殊问题: $k-\text{SAT}$. 在第五节中, 我们对 DPLL 所使用的核心规则: 单元子句传播 (Unit Propagation). 在剩下的几节中, 我们会描述 DPLL 算法, 并最后简单讨论算法的优化问题.
5.1 子句 (Clauses)
为了规避分裂法 (Splitting Method) 中由于对任意谓词公式的可满足性检查不能始终保证高效率的问题, 大多数的自动推理 (Automated Reasoning) 算法都使用 子句 作为可满足性检查的最小单位, 无论自动推理的作用域为谓词逻辑还是一节谓词逻辑都是如此.
这种选择的合理性有以下两点:
首先 (在后面我们对子句与合取范式定义的介绍中我们可以立即看出), 所有的针对任意谓词公式的可满足性检查问题都可以被转换为一个等价的, 针对一系列子句的可满足性的检查问题.
其次, 相比任意结构的谓词公式, 子句具有显著的结构简易的特点.
粗略地说, 在一个基于 子句 的可满足性检测问题中, 作为输入的谓词公式或者一系列谓词公式将首先被转换为一系列子句, 然后某个用于检测子句可满足性的算法会作用在这个由子句组成的集合上.
下面, 我们为 子句 给出精确的定义. 在引入子句的定义之前, 我们首先需要引入另一种特殊的谓词公式, 文字 (literal).
定义 5.1.1 (文字)
文字 或为某个原子公式 $A$ 本身或它的否定形式 (
negation) $\neg A$.若一个 文字 形为某个原子公式, 称其为 正的 (
Positive), 反之称其为 负的 (Negative).
我们随后定义 文字的补:
定义 5.1.2 (文字的补)
给定文字 $L$, 它的 补 $\widetilde{L}$ 定义为:
\[\widetilde{L} \overset{\text{def}}{=} \begin{cases} \neg L ~~~ \text{if L is positive} \\ ~~~L ~~~ \text{if L has the form} ~ \neg A\end{cases}\]
不难得出, 文字 $p$ 和 $\neg p$ 互为对方的 $补$. 并且, 显然地:
\[\widetilde{\widetilde{L}} = L.\]本质上, 文字就是原子公式的别名. 在完成对 文字 和 文字的补 的定义后, 我们下面引入 子句 的严格定义:
定义 5.1.3 (子句)
子句
clause本质上就是一系列文字 $L_1, L_2, \cdots, L_n, ~ n\geqslant0$ 的析取 $L_1 \vee L_2 \vee \cdots \vee L_n.$
下面再给出一些特殊形式子句的额外定义.
-
若 $n=0$, 称这样的子句为 空 (
empty), 用 $\square$ 表示. -
若 $n=1$, 此时子句恰由一个文字组成, 称这样的子句为 单位 (
unit). -
若组成子句的文字中 最多有一个为真, 称这样的子句为
Horn子句. -
类似地, 若组成子句的文字全为真, 称该子句也为 正的, 反之若全为假, 则称该子句为 负的.
结合上述定义, 我们同时可以得到以下结论:
- 显然, 任何单位子句都是
Horn子句. - 一个 正的 子句为
Horn子句, 当且仅当它或为单位子句, 或为空. - 任何 负的 子句都是
Horn子句.
我们下面考虑基于 文字 和 子句 框架下的可满足性.
首先, 对于 正的 文字 $p$, 任一解释 $I$ 满足它, 当且仅当 $I(p)=1$; 对于 负的 文字 $\neg p$, 满足它的解释 $I$ 需要满足 $I(p)=0$, 也就是 $I(\neg p) = 1$.
其次, 我们考虑子句. 由于子句本质上是一系列文字的析取, 因此若某个解释 $I$ 满足某个子句 $C$, 当且仅当该解释满足组成该子句的至少一个文字. 基于这个事实, 我们认为空子句实际上和 $\perp$ 等价, 因为任何解释 $I$ 都永无法满足空子句.
我们同时可以看到, 与空子句的永不可满足性相对, 任何非空的子句都是可满足的. 此外, 如果某个子句中同时包含相对的一对文字 $p$ 和 $\neg p$, 这个子句实际上就是一个重言式 (tautology), 因为无论 $p$ 取和值, 它恒为真.
相应地, 若某个子句中不包含任何一对相对的文字, 我们总可以构造出一个让它为假的解释 $I$:
\[I(p) = \begin{cases} 0 ~~~ \text{if literal p is positive} \\ 1 ~~~ \text{if literal p is negative}\end{cases}.\]从上面的讨论可以看出, 对单独某个子句的可满足性的检测是非常简单的, 但对于一系列子句而言则并非如此. 我们下面引入 合取范式 和 析取范式 的概念, 并借此说明任何形式的谓词公式的可满足性问题都可以被转化为某些子句的可满足性问题.
定义 5.1.4 (合取范式)
称一个谓词公式为 合取范式, 当且仅当它为 $\top, \perp$, 或为多个文字析取 (也就是子句) 的合取:
\[A = \bigwedge_{i} \bigvee_{j} L_{i,j}\]
定义 5.1.5 (析取范式)
称一个谓词公式为 析取范式, 当且仅当它为 $\top, \perp$, 或为多个文字合取的析取:
\[A = \bigvee_{i} \bigwedge_{j} L_{i,j}\]
我们称谓词公式 $B$ 为谓词公式 $A$ 的 合取 (析取) 范式, 当且仅当两个谓词公式 等价 且公式 $B$ 为 合取 (析取) 范式.
显然根据上述定义, 针对合取范式的可满足性问题实质上和针对一系列子句的可满足性问题是等价的.
5.2 向合取范式的转换
下面给出一个最基础的合取范式转换算法:
算法 5.2.1 (基础合取范式转换算法)
该算法基于下图展示的 改写律. 在不考虑同级符号下谓词文字的交换问题和结合问题 (也就是说, 我们认为它满足交换律和结合律) 的情况下, 通过多次应用改写律, 我们最终可以得到所输入算法的合取范式.
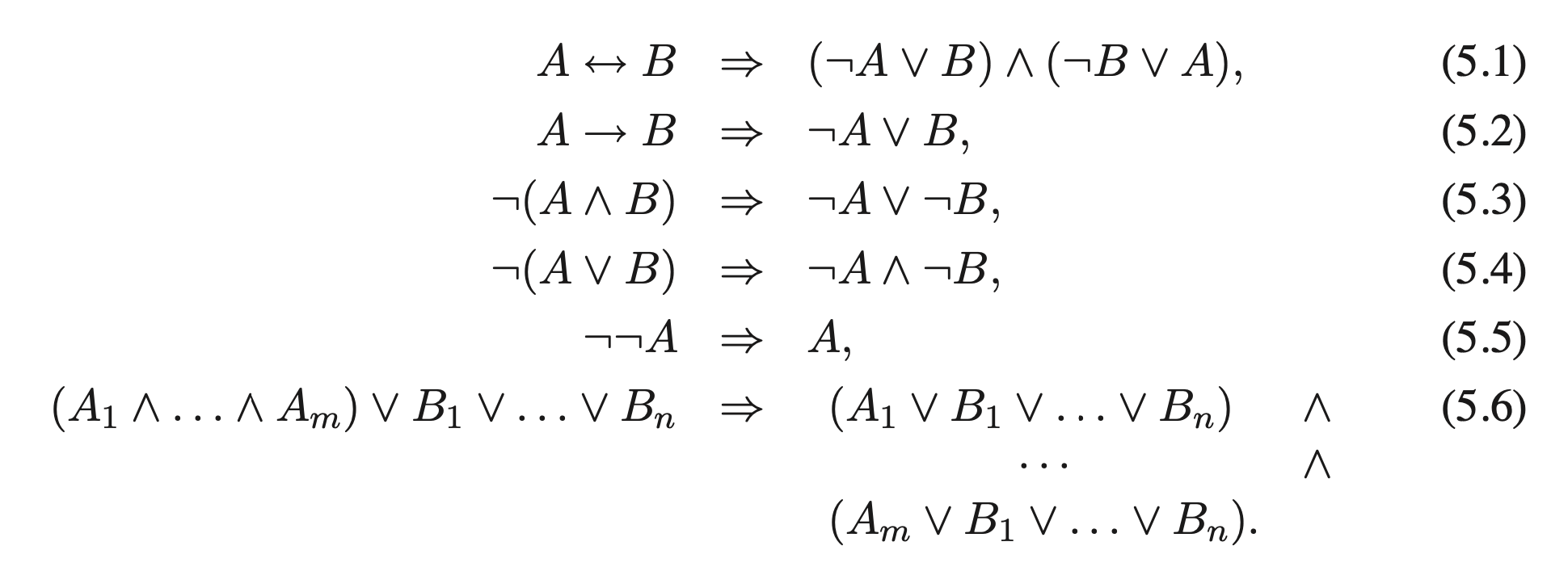

5.3 子句形式和定义变换
首先来用一个例子侧面说明引入 子句形式 的必要性.
考虑谓词公式
\[p_1 \leftrightarrow (p_2 \leftrightarrow (p_3 \leftrightarrow (p_4 \leftrightarrow (p_5 \leftrightarrow p_6))))\]不难看到, 在我们要采用基础合取范式转换算法尝试求得它的合取范式的过程中, 在改写律的规定下, 每一次对外层 $\leftrightarrow$ 的改写都会在原来包含子式 $p_5 \leftrightarrow p_6$ 的谓词公式基础上引入两个新的 $p_5 \leftrightarrow p_6$. 因此, 不难看出对于给定的谓词公式而言, 随着逐步应用改写律, 我们得到的新谓词公式中子式数量的增长速度将会是指数级别, 进一步处理如此复杂度的子式将会令其更加复杂, 这是在实际应用中绝不可接受的.
为了规避这一问题, 我们不再要求算法在对给定谓词公式进行转换后给出一个严格与之等价的新公式, 而将要求弱化到只需要给出一个在可满足性上与原公式相同的结果即可. 为了实现这一点, 我们下面对 定义 (命名) 和 子句形式 给出定义.
定义 5.3.1 (命名)
给定谓词公式 $P$, 称引入谓词变量 $n$, 规定 $n \leftrightarrow P$, 则原先包含 $P$ 的公式 $P \leftrightarrow Q$ 可被转换为:
\[n \leftrightarrow Q \\ n \leftrightarrow P\]我们称这个过程为 用 $n$ 对 $P$ 的命名, 并且称公式 $n \leftrightarrow P$ 为对变量 $n$ 的 定义.
命名的对象是某个已经存在的谓词公式, 定义的对象是某个尚不明确的谓词变量或公式. 命名的本质是用一个被定义为与原来的较为复杂的子式等价的谓词变量, 通过在原公式中对复杂子式的替换, 从而实现简化子式的效果. 在大部分情况下, 只要我们注意选择被 命名 的子式, 原公式的复杂度都可以得到相当程度的简化.
需要注意的是, 对给定谓词公式的某个或某些子式命名后得到的新公式和原来的并不等价:
考虑这样的例子. 不妨假设 $S$ 为一个只包含了一个谓词公式 $p$ 的集合, 可知 $S$ 的模型 (model) 即为所有使 $p$ 为真的解释 $I_S$. 若此时添加一个对 $p$ 的定义, 则有:
显然可知, $S’$ 的 模型为所有使得 $p$ 和 $q$ 为真的解释 $I_{S’}$ (因为我们需要让 $p$ 为真的同时 $p \leftrightarrow q$ 也为真, 那就只能确保 $p$, $q$ 同真), 自然 $I_{S} \neq I_{S’}$, 也就得到了 $S$ 和 $S’$ 不等价的结论.
为了进一步说明 命名 (定义) 的概念, 并便于我们将谓词公式转换为一系列子句, 我们下面引入 子句形式 的概念.
定义 5.3.2 (子句形式)
记 $A$ 为某个谓词公式. $A$ 的 子句形式 即为和 $A$ 共享可满足性的一系列子句.
也就是说, $A$ 为可满足的, 当且仅当 $A$ 的子句形式也是可满足的.
子句形式和合取范式最本质的区别在于它们和原公式之间的等价性不同. 子句形式只在可满足性上和原公式相同, 而合取范式是和原公式完全等价的. 这说明对任一谓词公式或一系列谓词公式, 我们总能找到一个足够短的子句形式. 通过定义变换所得到的新的谓词公式的长度增长速度将会是随着原谓词公式规模的增长的多项式级别而非基础合取范式转换算法的指数级别.
下面我们通过一个引理详细解释 命名 (定义) 的作用.
引理 5.3.1
设 $S$ 为一系列谓词公式, $B$ 为 $S$ 中的一个谓词公式, 记 $n$ 为一个不在 $B$ 和 $S$ 中出现过的谓词变量.
则 $S$ 为可满足的, 当且仅当 $S \cup {n \leftrightarrow B}$ 为可满足的. 注意我们一般记 $S \cup {n \leftrightarrow B}$ 为 $S’$.
证明
\[I'(q) \overset{\text{def}}{=} \begin{cases} I(B) ~~~ \text{if} ~q=n \\ I(q) ~~~~ \text{else}\end{cases}\]
必要性: 显然可知, $S \cup {n \leftrightarrow B}$ 的任一模型都是 $S$ 的一个模型, 故必要性成立. $\blacksquare$
充分性: 不妨假设 $S$ 在解释 $I$ 下为可满足的. 我们定义新的解释 $I’$ 如下:
显然, $I’$ 同时满足 $S$ 和在对 $B$ 命名的过程中新引入的公式 $n \leftrightarrow B$. 同时由于 $I’$ 对 $n$ 的解释完全不影响 $S$, 故 $I’$ 同时也是 $S$ 的一个模型, 且有 $I(B) = I’(B)$.
由 $I’$的定义我们又知, $I’(n) = I(B) \rightarrow I’(n) = I’(B)$. 因此, $I‘$ 也满足 $n \leftrightarrow B$. 由此可知, $I’$ 也是 $S \cup {n \leftrightarrow B}$ 的一个模型.
因此, 无论对于 $S$ 的任意一个模型 $I$, 我们总能基于它构造出一个 $S \cup {n \leftrightarrow B}$ 的模型, 记为 $I’$, 故充分性成立. $\blacksquare$
综上, “$S$ 为可满足的” 和 “$S \cup {n \leftrightarrow B}$ 为可满足的” 互为充要条件. $\blacksquare$
由此可见, 命名 (定义) 可以用于对某个谓词公式中的复杂且重复出现多次的子项进行命名并将其等价替换, 从而得到一个更加简化的式子. 我们下面介绍一个应用了这一技巧的算法:
算法 5.3.1 (定义变换)
我们可以使用如下的算法将任意谓词公式 $A$ 替换为一个由一系列子句组成的集合 $S$, 其中 $S$ 为 $A$ 的子句形式:
\[S \overset{\text{def}}{=} \{C_1, C_2, \cdots, C_n\}.\]
- 若 $A$ 本身已经是一系列子句 $C_1, C_2, \cdots, C_n$ 的合取: 则
若不然, 对 $A$ 中的每一个不是文字的子式 $B$, 我们定义一个执行转换的函数 $n(B)$:
\[n(B) \overset{\text{def}}{=} \begin{cases} B ~~~ \text{if} ~B~ \text{is a literal} \\ p_B ~~~ \text{else}\end{cases}\]并且记 $\widetilde{n}(B)$ 为 $n(B)$ 的否定. 我们基于如下的规则定义 $p_B \leftrightarrow B$:
\[p_B \leftrightarrow n(B_1) \wedge n(B_2) \cdots \wedge n(B_m)\]
i. 若 $B$ 形为 $B_1 \wedge B_2 \wedge \cdots \wedge B_n$, 则将对变量 $p_B$ 的定义:加入 $S$ 中, 也就是:
\[\begin{aligned} &\neg p_B \vee n(B_1), \\ &\cdots \\ &\neg p_B \vee n(B_m), \\ &\widetilde{n}(B_1) \vee \cdots \vee \widetilde{n}(B_m) \vee p_B \end{aligned}\]\[p_B \leftrightarrow n(B_1) \vee n(B_2) \cdots \vee n(B_m)\]
ii. 若 $B$ 形为 $B_1 \wedge B_2 \vee \cdots \vee B_n$, 则将对变量 $p_B$ 的定义:加入 $S$ 中, 也就是:
\[\begin{aligned} &p_B \vee \widetilde{n}(B_1), \\ &\cdots \\ &p_B \vee \widetilde{n}(B_m), \\ &n(B_1) \vee \cdots \vee n(B_m) \vee \neg p_B \end{aligned}\]\[p_B \leftrightarrow (n(B_1) \rightarrow n(B_2))\]
iii. 若 $B$ 形为 $B_1 \rightarrow B_2$, 则将对变量 $p_B$ 的定义:加入 $S$ 中, 也就是:
\[\begin{aligned} &\neg p_B \vee \widetilde{n}(B_1) \vee \widetilde{n}(B_2), \\ &n(B_1) \vee p_B, \\ &\widetilde{n}(B_2) \vee p_B\end{aligned}\]\[p_B \leftrightarrow \neg n(B_1)\]
iv. 若 $B$ 形为 $\neg B_1$, 则将对变量 $p_B$ 的定义:加入 $S$ 中, 也就是:
\[\begin{aligned} &\neg p_B \vee \widetilde{n}(B_1), \\ &n(B_1) \vee p_B \end{aligned}\]\[p_B \leftrightarrow (n(B_1) \leftrightarrow n(B_2))\]
v. 若 $B$ 形为 $B_1 \leftrightarrow B_2$, 则将对变量 $p_B$ 的定义:加入 $S$ 中, 也就是:
\[\begin{aligned} &\neg p_B \vee \widetilde{n}(B_1) \vee \widetilde{n}(B_2), \\ &\neg p_B \vee \widetilde{n}(B_2) \vee \widetilde{n}(B_1), \\ &n(B_1) \vee n(B_2) \vee p_B, \\ &\widetilde{n}(B_2) \vee \widetilde{n}(B_2) \vee p_B\end{aligned}\]最终将单位子句 $p_A$ 加到 $S$ 中.
我们同时可以得到:
引理 5.3.2
设 $S$ 为一系列谓词公式, $B$ 为 $S$ 中的一个谓词公式, 记 $p$ 为一个不在 $B$ 和 $S$ 中出现过的谓词变量.
设 $S’$ 为 $S$ 通过用 $p$ 替换掉至少一处正的 (或负的) $B$ 得到的一系列谓词公式, 则 $S$ 为可满足的, 当且仅当 $S‘ \cup {p \rightarrow B}$ (或$S‘ \cup {B \rightarrow p}$) 为可满足的.
证明
此处指考虑 $p$ 为正的情况, $p$ 若为负的话同理.
必要性: 设 $S$ 为可接受的, 则由
引理 5.3.1, 显然 $S’$ 是可接受的, 进一步 $S’ \cup {p \leftrightarrow B}$ 也是可接受的.由于显然 $S’ \cup {p \leftrightarrow B}$ 的任一个模型均为 $S’ \cup {p \rightarrow B}$ 的模型, 故对于 $S‘$ 的任一个模型, 我们可以相应地一步步构造出 $S’$ 的, $S’ \cup {p \leftrightarrow B}$ 的, 直到 $S’ \cup {p \rightarrow B}$ 的模型, 因此 $S’ \cup {p \rightarrow B}$ 也是可接受的. $\blacksquare$
充分性: 设 $S’ \cup {p \rightarrow B}$ 为可满足的, 要证 $S$ 也是可满足的. 取 $S’ \cup {p \rightarrow B}$ 的任意模型 $I$. 对 $\forall A \in S$, 由定义可知, $S’$ 中必存在某个子句 $A’$, 通过将 $A’$ 中的某 (几) 处 $p$ 用 $B$ 替代即可得到 $A$.
由于在我们的假设下这些 B 都以 正 的形式出现, 且我们有 $I \vDash A’, ~~ I \vDash p \rightarrow B$, 自然地有 $I \vDash A$, 充分性得证. $\blacksquare$
我们下面引入一个利用了上述引理进一步简化了转换过程的, 优化的定义转换算法:
算法 5.3.2 (优化的定义变换)
我们可以使用如下的算法将任意谓词公式 $A$ 替换为一个由一系列子句组成的集合 $S$, 其中 $S$ 为 $A$ 的子句形式:
\[S \overset{\text{def}}{=} \{C_1, C_2, \cdots, C_n\}.\]
- 若 $A$ 本身已经是一系列子句 $C_1, C_2, \cdots, C_n$ 的合取: 则
若不然, 对 $A$ 中的每一个不是文字的子式 $B$, 我们定义一个执行转换的函数 $n(B)$:
\[n(B) \overset{\text{def}}{=} \begin{cases} B ~~~ \text{if} ~B~ \text{is a literal} \\ p_B ~~~ \text{else}\end{cases}\]并且记 $\widetilde{n}(B)$ 为 $n(B)$ 的否定. 我们基于如下的规则定义 $p_B \leftrightarrow B$.
i. 若 $B$ 形为 $B_1 \wedge B_2 \wedge \cdots \wedge B_n$, 则将对变量 $p_B$ 的定义加入 $S$ 中:
| 极性 $+1$ | 极性 $-1$ |
|---|---|
| $p_B \rightarrow n(B_1) \wedge n(B_2) \cdots \wedge n(B_m)$ | $n(B_1) \wedge n(B_2) \cdots \wedge n(B_m) \rightarrow p_B$ |
| $\neg p_B \vee n(B_1),$ $\cdots$ $\neg p_B \vee n(B_m)$ |
$\widetilde{n}(B_1) \vee \cdots \vee \widetilde{n}(B_m) \vee p_B$ |
ii. 若 $B$ 形为 $B_1 \wedge B_2 \vee \cdots \vee B_n$, 则将对变量 $p_B$ 的定义加入 $S$ 中:
| 极性 $+1$ | 极性 $-1$ |
|---|---|
| $p_B \rightarrow n(B_1) \vee n(B_2) \cdots \vee n(B_m)$ | $n(B_1) \vee n(B_2) \cdots \vee n(B_m) \rightarrow p_B$ |
| $n(B_1) \vee \cdots \vee n(B_m) \vee \neg p_B$ | $p_B \vee \widetilde{n}(B_1),$ $\cdots$ $p_B \vee \widetilde{n}(B_m)$ |
iii. 若 $B$ 形为 $B_1 \rightarrow B_2$, 则将对变量 $p_B$ 的定义加入 $S$ 中:
| 极性 $+1$ | 极性 $-1$ |
|---|---|
| $p_B \rightarrow (n(B_1) \rightarrow n(B_2))$ | $(n(B_1) \rightarrow n(B_2)) \rightarrow p_B$ |
| $\neg p_B \vee \widetilde{n}(B_1) \vee n(B_2)$ | $n(B_1) \vee p_B,$ $\widetilde{n}(B_2) \vee p_B$ |
iv. 若 $B$ 形为 $\neg B_1$, 则将对变量 $p_B$ 的定义加入 $S$ 中:
| 极性 $+1$ | 极性 $-1$ |
|---|---|
| $p_B \rightarrow \neg n(B_1)$ | $\neg n(B_1)\rightarrow p_B$ |
| $\neg p_B \vee \widetilde{n}(B_1)$ | $n(B_1) \vee p_B$ |
v. 若 $B$ 形为 $B_1 \leftrightarrow B_2$, 则将对变量 $p_B$ 的定义加入 $S$ 中:
| 极性 $+1$ | 极性 $-1$ |
|---|---|
| $p_B \rightarrow (n(B_1) \leftrightarrow n(B_2))$ | $(n(B_1) \leftrightarrow n(B_2)) \rightarrow p_B$ |
| $\neg p_B \vee \widetilde{n}(B_1) \vee n(B_2),$ $\neg p_B \vee \widetilde{n}(B_2) \vee n(B_1)$ |
$n(B_1) \vee n(B_2) \vee p_B,$ $\widetilde{n}(B_2) \vee \widetilde{n}(B_2) \vee p_B$ |
最终将单位子句 $p_A$ 加到 $S$ 中.
5.4 SAT 和 k-SAT
通过上一节, 我们知道定义的子句形式变换 (Definitional Clausal Form Transformation) 可以在多项式时间内将对某个命题公式的可满足性问题转换为对一系列子句的可满足性问题. 下面我们对 “对一系列子句的可满足性问题” 本身进行简单讨论.
定义 5.4.1 (SAT)
记
SAT为这样的决策问题: 考虑一个有限的, 由子句组成的集合, 若该集合是可满足的, 则该决策问题的答案为 “是”, 反之为 “否”.
我们随后讨论的对象基本集中于能够有效求解 SAT 问题的算法. 下面对一些情况特殊的 SAT 给出定义:
定义 5.4.2 (k-SAT)
记正整数 $k$, 称 $k-\text{clause}$ 为恰包含$k$ 个文字的子句. 称
k-SAT问题为关于一系列最多含有 $k$ 个文字的子句的可满足性问题.
注:
- $2-\text{SAT}$ 问题可在多项式时间内求解.
- $k-\text{SAT}$ 在 $k \geqslant 3$ 的情况下为一个 $\text{NP}$-完全问题.
5.5 单位子句传播法
通过引入子句的概念, 我们可以引入一种新的, 用于 证明谓词公式的不可满足性 的方法: 单位子句传播.
定义 5.5.1 (单位子句传播法)
记 $S$ 为一系列子句, 称 $S’$ 是 通过单位子句传播法从集合 $S$ 得到的, 若 $S’$ 是通过多次重复下列的转换而从 $S$ 得到的:
若 $S$ 包含一个单位子句 (即一个只包含某个文字 $L$ 的子句), 则:
- 从 $S$ 中将任何形如 $L \vee C’$ 的子句移除.
- 将 $S$ 中任何形如 $\widetilde{L}\vee C’$ 的子句替换为 $C’$.
在该过程中, 每一次执行转换时对我们起初所选取的单位子句进行的消除都会在整个集合中自顶而下, 自左而右的传播, 如同一道道涟漪. 随着转换的不断执行, 集合被不断简化, 直到最终一无所剩 (如果该子句集合具备可满足性的话), 一切重新归于平静.
通过应用单位子句传播法, 我们可以快速高效地检查复杂谓词公式的子句形式的不可满足性:

5.6 Horn SAT
本节中, 我们将说明单位子句传播法同样可用于求解一系列 $\text{Horn}$ 子句的可满足性问题.
首先说明一个所有由一系列子句组成的具备不可满足性的集合的共同性质:
引理 5.6.1
记 $S$ 为具不可满足性的, 由一系列子句组成的集合. 则 $S$ 至少包含一个 正子句 和至少一个 负子句.
证明
此处只列出对正子句存在性的证明, 负子句的存在性与其类似.
不妨假设 $S$ 中不存在任何正子句, 则 $S$ 中的每个子句都是负的.只需构造解释 $I$ 令所有谓词变量在该解释下均为假, 则这个解释 $I$ 就是可满足 $S$ 的, 和原假设 ”$S$ 是不可满足的“ 矛盾. 故 ”$S$ 中正子句不存在“ 的假设矛盾, 进而得 $S$ 中至少存在一个正子句. $\blacksquare$
定理 5.6.1
设 $S$ 为由一系列 $\text{Horn}$子句组成的集合, $S’$ 为 $S$ 通过单位传播法得到的新子句集合, 则 $S$ 具可满足性, 当且仅当 空子句 $\square \notin S’$.
证明
由单位传播法保持可满足性可知, 只需证 $S’$ 具可满足性, 当且仅当 空子句 $\square \notin S’$. 显然任何具可满足性的子句集合不可能包含空子句 $\square$. 下面证明若 $S’$ 具不可满足性, 则它包含 $\square$.
由于单位传播法应用于一系列 $\text{Horn}$ 子句得到的结果还是一系列 $\text{Horn}$ 子句, 故由
引理 5.6.1可知 $S’$ 必包含一个正子句. 由于正的 $\text{Horn}$ 子句或为单位子句或为空子句, 而 $S’$ 为单位传播法的结果, 不可能包含单位子句, 故 $S’$ 一定包含空子句. $\blacksquare$
由此可以看出, 定理 5.6.1 给出了一个用于检查一系列由 $\text{Horn}$ 子句构成的集合 $S$ 的可满足性的简易方法, 在对其应用单位传播法后, 我们只需检查得到的结果中是否含有空子句即可, 若它不含空子句, 则原集合具可满足性, 反之则不具备.
显然, 单位传播法的时间复杂度最多为多项式级别. 实际上, 通过使用恰当的数据结构, 我们还可以得到更强的结果:
定理 5.6.2
对一系列由 $\text{Horn}$ 子句的可满足性检查可在 线性时间内 完成.
5.7 DPLL
在上面的几节中, 我们介绍了一种用于简化由一系列子句组成的集合的方法: 单位传播法, 并且在上一章中展示了一种特殊情况: 我们可以仅仅使用单位传播法就能检测一种特殊的子句集合: $\text{Horn}$ 子句集合的可满足性.
然而, 单位传播法在本质上还仅是一种简化法, 而必须和其他的可满足性检测法结合才能实现最优性能. 本章中我们介绍一种结合了单位传播法和切分法的可满足性检测算法: DPLL.
定理 5.7.1 (DPLL)
下列图片展示了
DPLL算法的基本流程. 在该算法中, 从某个由一系列子句组成的集合中抽取子句的方法和对子句集合应用单位传播法的方法分别被参数化为select_literal()和propogate().

下面来看一个例子:

我们可以将 DPLL 对子句集合的处理的过程可视化为一棵 决策树. 在 DPLL 给出 “给定子句集合具备可满足性” 的结论后, 我们一般需要找出一个满足该集合的解释. 我们可以通过下列的定理实现这一点:
定理 5.7.2 (模型构造定理)
设
\[I(p) = \begin{cases} 1~~~ \text{if} ~ p \in \mathscr{L} \\ 0~~~ \text{if} ~ \neg p \in \mathscr{L}\end{cases}.\]DPLL作用于子句集合 $S$ 得到的结果为 “该集合具备可满足性”, 设 $\mathscr{L}$ 为由所有在DPLL的处理决策树中导致最终得到空子句 (空子句集) 的分支上所有文字组成的集合, 则至少存在一个解释 $I$ 使:并且任何满足上述性质的解释 $I$ 都满足 $S$: $I \vDash S$.
证明
设文字 $L \in \mathscr{L}$, 也就是说 $L$ 在单位传播法的应用过程中被使用过, 故显然 $\widetilde{L} \notin \mathscr{L}$, 故至少存在一个解释 $I$ 满足定理条件.
下面证明对任何满足条件的解释 $I$, 它都满足 $S$:
只需注意, 在
DPLL算法的任何一步中被移除的子句 $C$ 都在 $\mathscr{L}$ 中包含一个文字. 由于子句是一系列文字的析取, 故 $I \vDash C$.由假设 $S$ 具可满足性, 故其中所有的子句最终都被
DPLL移除, 也就是说该集合中的所有子句军备该解释满足, 故有 $I \vDash S$. $\blacksquare$
5.8 优化与实现
DPLL 的核心逻辑已经足够简单以至于难以进一步优化. 行之有效的优化手段一般从算法效率方面入手. 在此我们介绍两种针对 DPLL 逻辑的优化: 重言式消除 (Tautology Elimination) 和纯文本法则 (Pure Literal Rule).
重言式消除
显然, 重言式必然是可满足的, 因此将它们从子句集合中移除不会对原集合的可满足性产生任何影响.
由于 DPLL 执行过程中不会引入任何新的重言式, 我们只需要在算法执行前对给定的子句集合执行一次重言式消除, 就有可能通过消除集合中的所有重言式而对其简化.
纯文本法则
我们称谓词原子 $p$ 在子句集合 $S$ 中只有 正事件 (Positive Occurrences) 若 $S$ 不包含任何形如 $\neg p \vee C$ 的子句.
相应的, 负事件 (Negative Occurrences) 指在 $S$ 中不包含任何形如 $p \vee C$ 的子句 的原子谓词 $p$.
定义 5.8.1 (纯文本)
称子句集合 $S$ 中出现的 文本 $\widetilde{L}$ 为 纯文本, 若 $S$ 不包含任何形如 $\widetilde{L} \vee C$ 的子句.
本质上, 纯文本法则会将一个子句集合中所有包含纯文本的子句全部移除.
在 DPLL 中, 我们可以通过计算每个文本 $L$ 在子句集合中出现的次数判断它是否为纯文本.
一般来说, 我们使用 回溯算法 实现 DPLL. 我们会在函数 select_literal() 选取下一个文本 $L$ 时记录当前的状态, 随后对集合 $S \cup {L}$ 进行搜索. 而在搜索结束后, 通过恢复, 我们可以回到原来的状态并转而搜索另一分支 $S \cup {\widetilde{L}}$.
在 DPLL 的搜索过程中应用回溯算法会导致它的搜索次数呈指数级别, 因此对 select_literal() 选择下一文本的规则进行优化是至关重要的. 在这里我们不再介绍对算法效率本身的优化方法, 本章到此结束. $\blacksquare$
