Prolog 入门: 递归
在本章中, 我们将介绍 Prolog 中的递归定义, 并举例说明一个问题: Prolog 程序的 声明性含义 与 过程性含义 之间可能会存在不匹配的情形.
1. 递归定义
在 Prolog 中, 谓词可以被 递归地 定义. 简单来说, 如果一个谓词的定义中至少有一条规则包含了其本身, 则称它是 递归地定义 的.
我们首先考虑下列的知识库:
1
2
3
4
5
6
7
8
is_digesting(X, Y) :- just_ate(X, Y).
is_digesting(X, Y) :-
just_ate(X, Z),
is_digesting(Z, Y).
just_ate(mosquito,blood(john)).
just_ate(frog,mosquito).
just_ate(stork,frog).
上述的知识库中定义了 $3$ 条事实和 $2$ 条规则. 同时, 可以看出谓词 is_digesting 也是递归定义的, 因为在第二行对其的定义中出现了它自身. 而最重要的是, 由于 (并不是递归定义的) 第一条规则的存在, 我们可以从从第二条规则所构造的无限递归 (循环) 中挣脱出来. 下面我们分别对我们构造的知识库的 声明式含义 和 过程式含义 进行讨论.
“声明” (declarative), 即指给定 Prolog 知识库的逻辑含义. 也就是说, Prolog 知识库的 声明式含义 所描述的就是 “这个知识库说了什么”, 或者 “从逻辑的角度上看, 这个知识库告诉了我们什么”.
我们在知识库中所定义的两条规则从声明式含义的角度理解就是:
1
2
3
4
5
6
7
% If X has just eaten Y, then X is now digesting Y.
is_digesting(X, Y) :- just_ate(X,Y).
% If X has just eaten Z and Z is digesting Y, then X is digesting Y, too.
is_digesting(X, Y) :-
just_ate(X, Z),
is_digesting(Z, Y).
这两条规则显然在声明式含义的解释下都是符合逻辑的.
下面我们需要考虑这条递归定义的规则在 过程式含义 的解释下的真实含义, 也就是说, 当我们的某条查询指令用到了或者涉及到它时, 这条递归定义究竟会做什么.
对于常规的非递归规则而言, 它在过程式含义的解释下意义非常显然. 而对于本例提及的第二条递归定义而言, 这样的定义使 Prolog 可以使用这样的策略判断 is_digesting(X, Y): 尝试找到某个 Z, 并且它满足: 1. just_ate(X, Z) 为真; 2. is_digesting(Z, Y) 为真. 换句话说, 该条规则的定义使 Prolog 将执行证明搜索寻找可行解的任务切分为两个子任务. 理想状态下, 通过检索知识库, 两个子任务都能够得到解决, 从而原任务相应地也得到了解决.
我们下面考虑查询语句 is_digesting(stork,mosquito)..
基于上一章所介绍的证明搜索流程, 我们知道 Prolog 首先会尝试联合知识库中的第一条规则. 通过对变量 X 和 Y 进行实例化 (与规则中的项联合), 我们可以得到一条并不存在于知识库中的规则
1
just_ate(stork, mosquito).
第一条解路径并不能满足目标, 因此 Prolog 回溯至原点尝试第二条规则. 经过联合后程序需要满足的目标变为:
1
2
just_ate(stork, Z),
is_digesting(Z, mosquito).
也就是说, Prolog 需要找到一个同时满足两条目标的值为变量 Z 赋值.
经过对知识库的检索, Prolog 可以找到一个满足第一条目标的值 frog. 并且在尝试满足第二个目标时, 由于 第一条规则的存在, 我们可以通过推导 is_digesting(frog,mosquito). 得到位于知识库中的事实 just_ate(frog,mosquito)., 最终完成证明搜索.
从这个例子中不难看出, 形如第一条规则一般, 允许 Prolog 在执行对递归定义的证明搜索中最终跳出递归的规则是至关重要的 我们一般称其为
基本子句 (Escape Clause, or Base Clause). 倘若我们的知识库中不存在这样的基本子句, Prolog 就会重复执行无意义的计算而无法自拔.
我们再来看一个将递归应用于 Prolog 程序设计中的例子, 体会通过应用递归的概念, 我们是如何轻松愉快地定义 后代 (descendent) 的概念的.
首先给定一个记录了关系 child(X, Y) 的知识库:
1
2
child(bridget, caroline).
child(caroline, donna).
可见 Caroline 是 Bridget 的孩子, 而 Donna 又是 Caroline 的孩子. 我们下面首先尝试使用 非递归定义 对 后代 这一概念建模. 我们可以给出如下定义:
1
2
3
descend(X, Y) :- child(X, Y).
descend(X, Y) :- child(X, Z),
child(Z, Y).
如此我们就定义了深度为 2 的 后代 关系. 但是不难看出, 使用这种方式进行的定义不具备任何可扩展性, 当我们需要考虑深度更高的 后代 关系时, 它就不再适用了. 随着深度愈发递增, 我们需要为每一层 后代 关系单独定义, 此时我们的知识库大小就要被迫膨胀到不可描述的级别.
实际上, 我们不难观察到 后代 这一待建模的概念具有传递性. 基于传递性, 首先显然有:
1
2
3
%Y is a child of X, if...
descend(X, Y) :- child(X, Z), % 1. Z is a child of X
descend(Z, Y). % 2. Y is a descendant of Z
不难看出上述的递归子句具有高度的可扩展性. 并且在深度为 $1$ 时, 后代 和 孩子 的定义具有等价性:
1
descend(X, Y) :- child(X, Y).
将两条规则拼接即可得到由一条 基本子句 和一条 递归子句 组成的 完整的 递归定义. 在使用结合了递归定义的规则的知识库进行查询时, Prolog 在每一次搜索证明中都会首先尝试联合基本子句以尝试满足当前目标, 而若不满足的话就联合第二条递归子句将问题进一步变换. 最终, 我们可以得到一条形如下图的搜索树.
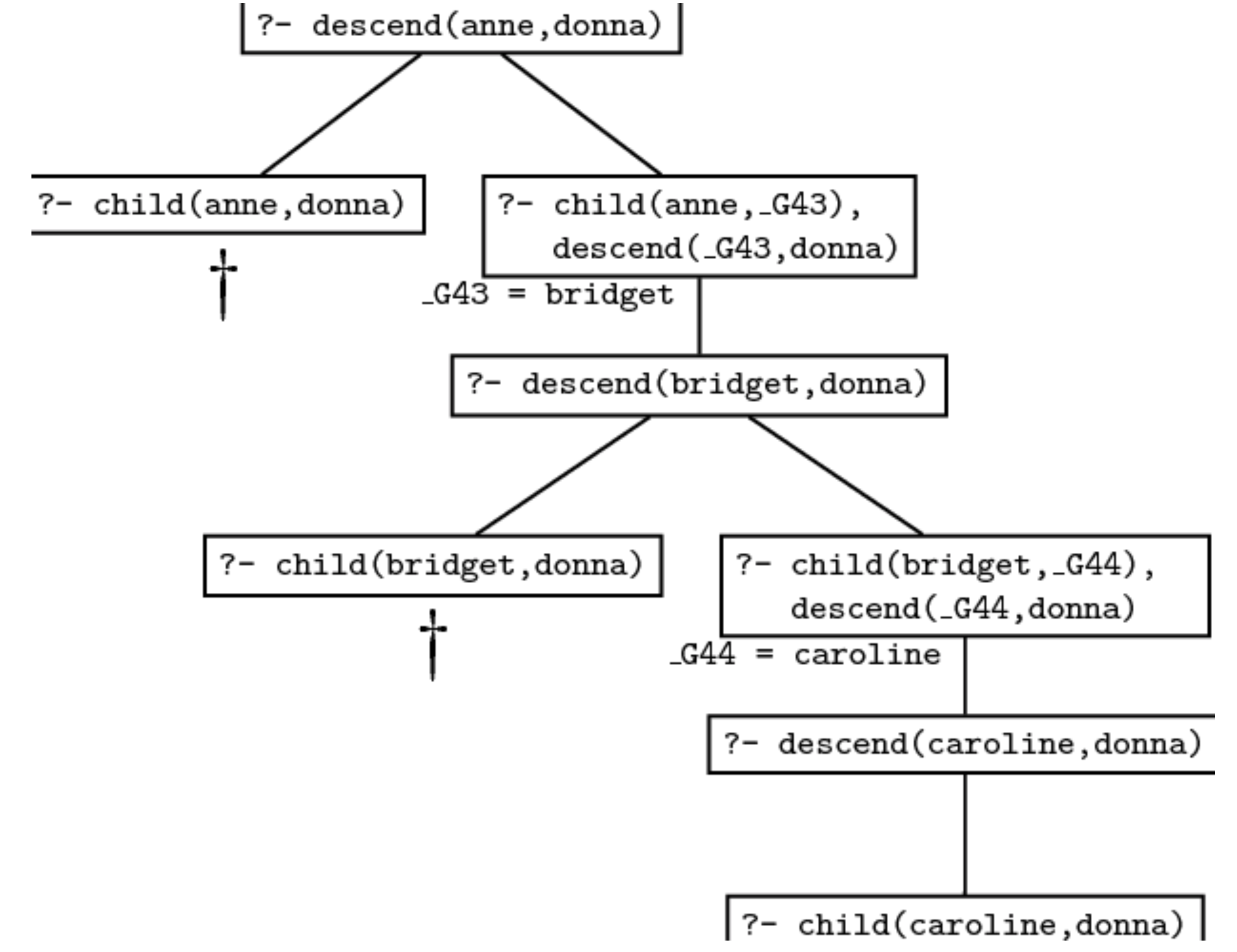
得益于递归子句的结构性和定义本身的可扩展性, 我们可以使用简单的递归子句实现定义, 并在需要的情形下轻松地通过递归将定义的深度扩展到需要的级别而无需让定义本身复杂化.
我们再来看一个利用递归定义在 Prolog 中实现 计数 的例子.
我们使用一种递归定义进行数字表示:
- 定义 $0$ 为数字.
- 若 $X$ 为一个数字, 它的后继数字 (
Successor) $\text{succ}(X)$ 也是一个数字.
显然, 上述的定义也是递归的, 并且性质 “数字” 同样具有传递性. 定义知识库
1
2
numeral(0).
numeral(succ(X)) :- numeral(X).
则我们在执行查询 numeral(X). 时, 可以在每一次证明搜索得出结果后使用预置谓词 ; 强制 Prolog 回溯, 而在这一过程中, 我们实际上通过回溯后的新的联合得到了新的数字:
1
2
3
4
5
6
7
8
9
10
X = 0 ;
X = succ(0) ;
X = succ(succ(0)) ;
X = succ(succ(succ(0))) ;
X = succ(succ(succ(succ(0)))) ;
X = succ(succ(succ(succ(succ(0))))) ;
X = succ(succ(succ(succ(succ(succ(0)))))) ;
X = succ(succ(succ(succ(succ(succ(succ(0))))))) ;
X = succ(succ(succ(succ(succ(succ(succ(succ(0))))))))
yes
在此基础上, 我们以介绍一个递归定义的加法来结束本章.
利用在上一个例子中定义的, 递归的数字表示法, 我们来尝试递归地定义加法. 考虑一个三元谓词 add(X, Y, Z): 给定三个变量, 它的功能是将 X+Y 赋值给 Z, 如下列的代码片段所示:
1
2
3
4
5
?- add(succ(succ(0)), succ(succ(0)),
succ(succ(succ(succ(0))))).
yes
?- add(succ(succ(0)), succ(0),Y).
Y = succ(succ(succ(0)))
对加法中可能出现的情形进行分别考虑, 我们有:
- 若给定的首个参数
X为 $0$, 则返回参数Z的值恒等于Y:1
add(0, Y, Y).
-
若给定的前两个被加数均不为 $0$, 设 $X$ 为某个已知的数 $X_1$ 的后继数字, 则不难从 $X_1 + Y$ 计算出 $X + Y$: 后者自然也是前者的后继数字, 在形式上只是相差一个函子而已. 由于我们希望从较大的后继数字反推它的前继, 从而利用
succ()谓词的计数特性计算累加结果, 故我们定义递归子句如下:1
add(succ(X), Y, succ(Z)) :- add(X, Y, Z)
下面以 add(succ(succ(succ(0))), succ(succ(0)), R). 为例说明 Prolog 在执行 add()/3 语句时的证明搜索过程.
由于首位变量非 $0$, Prolog 会跳过无法执行联合的第一条规则, 也就是我们定义的基本子句, 而尝试将查询语句与第二条递归子句联合. 在联合时, 首位 succ(succ(succ(0))) 最外层的函子 succ() 被剥离, 第二位维持不变, 然后分别作为递归查询语句 add(X, Y, Z) 的前两个参数. 而查询语句的末位参数被赋予为一个尚未实例化的临时值 (这是显然的, 因为此刻我们并不知道该给它赋什么值才能满足目标), 不妨记其为 _G648. 需要注意的是, 此时我们已经可以确定 _G648 和原语句中 R 的关系, 因为当这个查询语句和递归子句的谓词左侧的项 add(succ(X), Y, succ(Z)) 联合时, R 显然会被实例化为 succ(_G648). 也就是说, 此时 R 实际上是一个以某个值未知的变量 _G648 为参数的复合项 succ(_G648).
随后, Prolog 会尝试对这个通过联合递归子句得到的递归查询语句执行证明搜索, 从而在得到新的递归查询语句的同时, 一层层地剥离 succ() 函子直到剥出最内层的 0. 该过程的搜索树如下图所示:
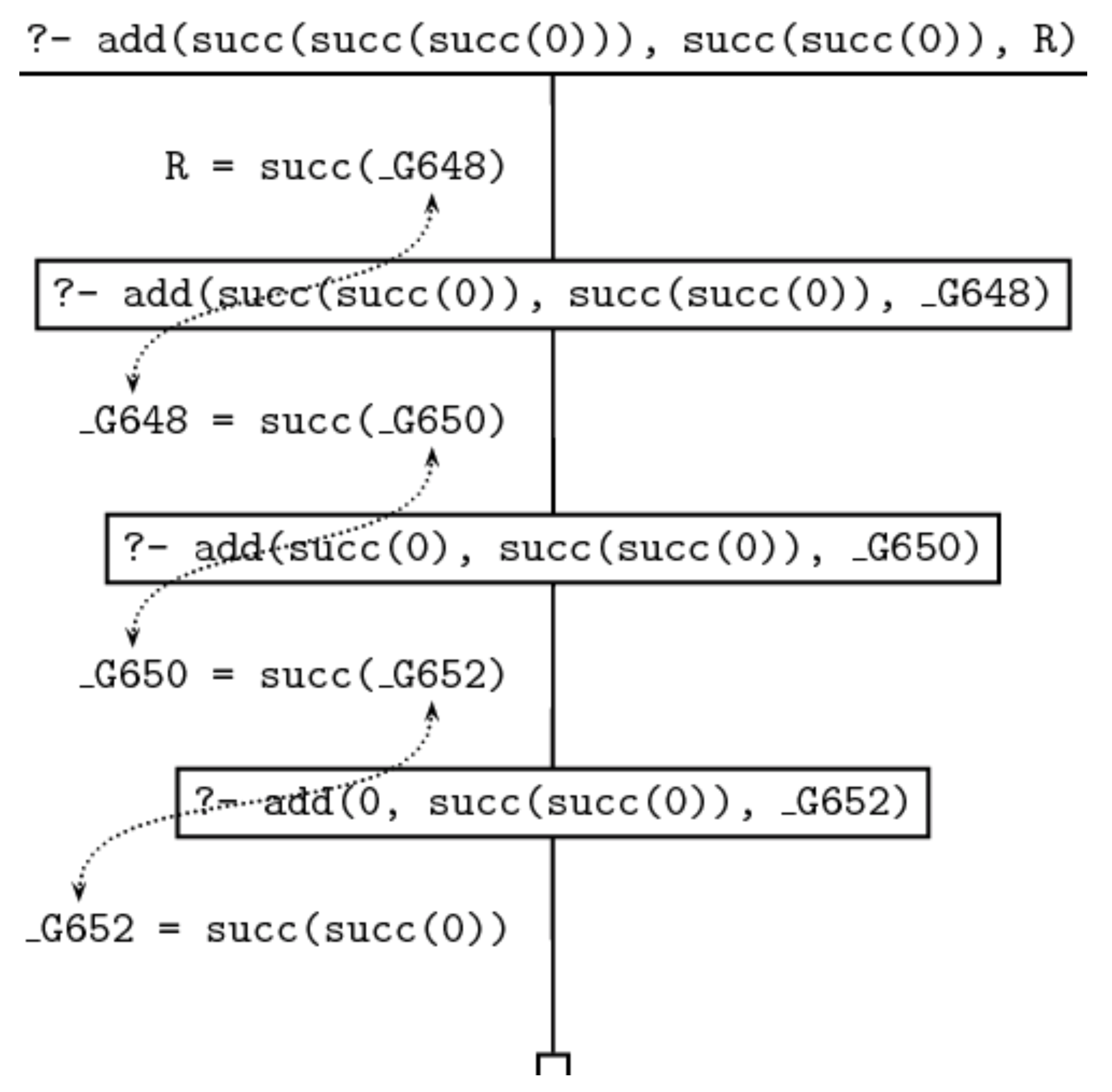
此时, 要满足当前目标, 我们只需要将语句与知识库中的第一条基本子句联合, 这样就得到了计算加法的结果: succ(succ(0)).
2. 规则顺序, 目标顺序与程序可终止性
在典型的 “逻辑程序设计语言” 中, 程序设计者不需要具体地告知计算机需要执行的指令是什么, 而应该只向计算机展示对 问题本身的描述, 并让计算机 (中运行的逻辑程序设计环境) 基于某种规则自行求解.
然而需要注意的是, Prolog 并不是完全和这样的 “逻辑程序设计语言” 划等号的: 我们在讨论递归定义时就已经了解到, 在一些特定情形下对某些 Prolog 程序进行 描述性解释 和 过程性解释 所得到的含义是截然不同的. 本质上而言, Prolog 处理用户查询的过程实际上是在执行对给定知识库的, 自上而下, 自左而右的检索. 下面我们再用一个简单的例子说明一个事实: 知识库中规则和目标语句的顺序会影响程序的执行情况, 求解速度, 甚至程序的可终止性.
首先考虑如下的知识库:
1
2
3
4
5
6
7
8
9
child(anne, bridget).
child(bridget, caroline).
child(caroline, donna).
child(donna, emily).
descend(X, Y) :- child(X, Y).
descend(X, Y) :- child(X, Z),
descend(Z, Y).
随后将两条规则的顺序对换. 这样就得到了:
1
2
3
4
5
6
7
8
9
child(anne, bridget).
child(bridget, caroline).
child(caroline, donna).
child(donna, emily).
descend(X, Y) :- child(X, Z),
descend(Z, Y).
descend(X, Y) :- child(X, Y).
从逻辑上看, 对规则顺序的更改没有对程序的含义造成任何影响. 但这样的对换从过程上 (略微地) 改变了程序本身: Prolog 基于两个知识库进行同一个查询语句的证明搜索后, 得到的第一个解很可能是不同的. 也就是说, 对规则顺序的更改往往会导致程序求解过程行为的变更.
我们下面再考虑对规则内部目标顺序的变更. 我们对换规则
1
2
descend(X, Y) :- child(X, Z),
descend(Z, Y).
中目标 child(X, Z) 和 descend(Z, Y) 的顺序, 就得到了
1
2
3
4
5
6
7
8
9
child(anne, bridget).
child(bridget, caroline).
child(caroline, donna).
child(donna, emily).
descend(X, Y) :- descend(Z, Y),
child(X, Z).
descend(X, Y) :- child(X, Y).
同样, 我们所得到的新知识库从逻辑上看与原先的没有任何区别. 但是这一知识库在用作对语句
1
descend(anne, emily).
查询的参考时就会出现明显的问题:
根据 Prolog 证明搜索的顺序, 它总是会优先尝试位置靠前的规则. 因此, 在尝试将语句和
1
descend(X, Y) :- descend(Z, Y), child(X, Z).
联合时, 它需要找到一个变量 $W_1$ 使目标 descend(W1, emily) 成立. 而为了满足这一目标, 由于 Prolog 总会优先尝试联合第一个子目标, 问题就被转换为本质上毫无变化的: “找到变量 $W_2$ 满足目标 descend(W2, emily)”. 由于在一次次的转换中问题没有得到任何变化和求解的进展, 程序会无休止地运行下去直到超出内存限制.
我们最后考虑如下的知识库:
1
2
3
4
5
6
7
8
9
child(anne, bridget).
child(bridget, caroline).
child(caroline, donna).
child(donna, emily).
descend(X, Y) :- child(X, Y).
descend(X, Y) :- descend(Z, Y),
child(X, Z).
它和上一个知识库的差别仅在于两条规则的顺序, 因此在逻辑上它们仍然是完全相同的. 由于它仍然包含一条以递归定义作为第一个子目标的规则, 对某些查询语句而言它仍然是不可终止的, 比如
1
descend(anne, emily).
但是和上一个知识库不同的是, 对于某些无法在上一个知识库中求解的查询语句, 它却可以找出可行解:
1
descend(anne, bridget).
这告诉我们, 对于某些不具备可终止性的 Prolog 程序而言, 改变知识库中规则的顺序可能会让我们找到额外的可行解. 同时我们也不难看到, 规则语句中子目标的顺序具备 过程重要性, 正是它决定了程序是否具备可终止性.
总的来说, 对 Prolog 程序知识库中规则顺序的对换往往会影响程序求解的流程, 对规则内部子目标顺序的对换会影响该程序的可终止性. 对于不具备可终止性的程序而言, 对换知识库中规则的顺序有可能让我们得到本无法求得的额外可行解.
从程序设计的角度来看, 这意味着我们在设计 Prolog 程序时不仅要考虑到知识库在逻辑角度上的含义, 同时需要额外关注知识库中规则的形态和顺序编排会如何对 Prolog 在该知识库上进行查询时的行为造成影响. 同时, 在设计递归定义时我们还需要额外注意它的可终止性: 我们需要满足的最基本要求就是, 确保存在合理的基础语句, 并且尽可能地将具有递归特性的子目标顺序排在不具有递归特性的子目标之后.
