Prolog 入门: 联合与证明搜索

在本章中, 我们将对 Prolog 中 联合 的定义和性质作简单介绍, 引入两个内置谓词 = 和 unify_with_occurs_check, 并区分它和常规的 联合 的差别.

此外, 我们还将解释 Prolog 是如何使用 肯定前件式假言推理 (MP, Modus Ponens) 从已知信息得到新结论的.

1. 联合

我们首先给出 联合 的定义:

定义 (联合)

两个项可以被联合, 当且仅当:

1. 它们或是相同的项
2. 或这些项中包含了可以 (同时) 通过与项一并实例化使得这两个项相同的变量.

显然, 基于上述定义, 可以立即得知, student(axton)和 student(axton) 这两个项因为完全相同故可被联合, rhythm_game_player(axton) 和 rhythm_game_player(tom) 既不相同, 也不包含任何可以通过实例化而使得两个项相同, 因此它们无法被联合.

类似地, likes(axton, X) 和 likes(axton, cytusii) 是可以被联合的, 因为我们显然可以通过对变量 X 进行赋值使两个项相同; 而 likes(axton, cytusii) 和 likes(Y, arcaea) 则是不可以被联合的, 因为我们永远无法通过对 Y 进行赋值而使这两个项相等.

我们下面对 Prolog 判定 联合 的规则作更严格的定义:

定义 (联合规则)

在 Prolog 中, 我们称两个项可被联合, 当且仅当它们同时满足下述三条规则:

1. 若两个项均为 常量 (Constants), 当且仅当它们为同一个原子或同一个数字时, 两项联合.
2. 若 项1 为变量而 项2 为任何类型的项, 则两项联合,且此时变量被实例化为 项2, 反之亦然. 若两项均为变量, 则在联合过程中被互相实例化. 称它们的值共享. (share values).
3. 若两项均为复杂项, 则其联合当且仅当:
   3.1 函子和元 (functor and arity) 相同.
   3.2 所有对应的参数都可联合.
   3.3 变量实例化过程是无冲突的, 例如不存在 “必须让某个变量同时在两个不同的位置上取不同的值才能满足对应参数可联合” 的情况.

同样我们举几个例子说明一下上述的联合规则.

首先, 我们可以选择下列的任一方式使用 = 谓词:

1
2
3
4
5
% a rather unnatual notation
?- =(axton, axton).

% the most common one: infix notation
?- axton = axton.

其次:

1
2
3
4
5
6
7
8
9
10
11
% fits clause 1
?- axton = axton
true.

% fits clause 1: both terms are numbers
?- 114514 = 114514.
true.

% doesn't fix: atom 'axton' and 'ryan' are different
?- axton = ryan.
false.

注意此处 Prolog 的一个特性:

1
2
3
4
% quirk: prolog will consider any atoms of the form 
% 'symbols' as the atom of form symbols.
?- 'axton' = axton.
true.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
% clearly the variable can unify with the constant following clause 2.
?- axton = X.
true.

% now consider complex terms.
?- k(s(g), Y) = k(X, t(k)).
true.
% clearly it's true as long as s(g) = X, and Y = t(k), 
% which follows clause 3.

% the last example
?- loves(axton, phigros) = loves(X, X).
false.
% this will not work, as it violates clause 3: the cariable instantiation is incompatible.

我们最后介绍 Prolog 处理联合时的一个可能导致问题的策略.

考虑一个对象为某个变量 X 和一个包含该变量的项 axton(X) 的联合 X = axton(X).

若要执行关于一个变量和一个项之间的联合, 对于常规的联合算法, 它首先会检测项中是否也包含了那个变量, 这一过程就叫做 Occurs Check. 若确实如此, 该算法会认为该联合不可执行, 因为无论我们将变量 X 实例化为任何值, 由于该变量同时作为项的参数, 因此谓词 = 两侧永远不等, 不满足联合规则的任意一条, 因此联合无法执行.

但对于 Prolog 而言, 由于联合是该语言中最基础的操作之一, 因此出于优化性能和运算速度的考量, Prolog 被设计为在执行联合前刻意跳过 Occurs Check 而直接尝试执行联合. 这一策略将导致它原则是在执行这样的联合时会陷入无限循环而无法自拔, 直到超出内存限制. 实际上, 它在递归超过固定步数后会返回类似于如下的信息:

1
2
3
?- X = axton(X).
X  =  axton(axton(axton(axton(...)))))))) 
yes.

可以看到其输出和标准的联合算法在处理这样的联合时输出的结果是不同的.

不过, Prolog 内置了一个用于以标准联合算法执行联合操作的谓词: unify_with_occurs_check. 使用这一谓词处理这样的联合, 我们就能得到正确的结果.

2. 证明搜索

在完成对联合的学习和了解后, 我们下面讨论 证明搜索 (Proof Search).

为了更清晰地明确证明搜索的过程, 我们先来看一个例子.

首先我们定义下列的知识库:

1
2
3
4
5
6
7
8
9
10
11
12
13
% facts for f()
f(a).
f(b).

% facts for g()
g(a).
g(b).

% facts for h()
h(b).

% predifine a rule
k(X) :- f(X), g(X), h(X).

编译加载后, 查询语句 k(Y). 则很显然, 我们所预期的答案自然是 k(b). 下面我们来考虑 Prolog 对该问题的求解过程.

Prolog 对问题的求解流程基本上是基于给定的知识库, 自顶而下地尝试将用户的查询语句和知识库中的某条事实或定义的某个规则相联合. 显然, 在当前考虑的例子中, Prolog 只能将查询语句 k(Y) 和 规则 k(X) :- f(X), g(X), h(X). 联合.

在将用户查询语句中的变量 (在这里是 Y) 与知识库中的某个事实中的变量或规则相联合时, Prolog 会生成一个随机的新变量用于指代这些在规则中共享的变量. 不妨假定:

1
k(_G34)

则此时可知

1
k(_G34)  :-  f(_G34),  g(_G34),  h(_G34).

也就是说, 我们将意为 “我想要找到满足条件 k 的项” 的用户查询语句转换为了规则: “这样的项满足条件 k, 当且仅当它同时具备性质 f, g 和 h”. 也就是说, 下面的任务就是要找到同时满足这三个性质的项.

从此处开始我们将处理用户查询的过程以抽象图形表示. 箱盒中的或为查询, 或为目标; 竖线表示某个联合过程, 而横线下方的文字为经过联合过程后我们得到的目标.

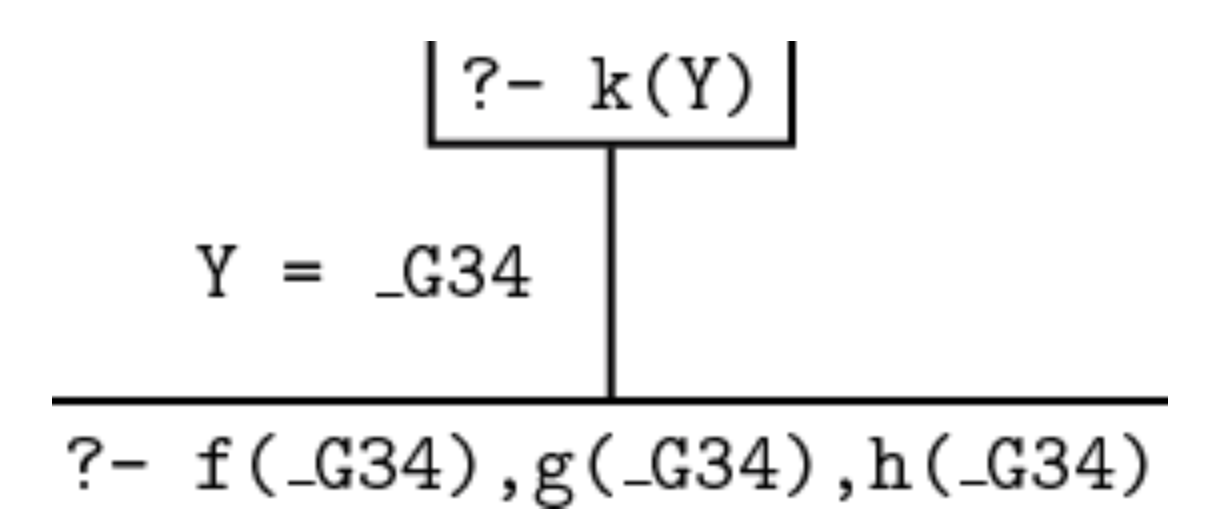
在得到了一列 (a list of, 我们进一步将它们抽象为一个存储目标的列表) 要满足的目标后, Prolog 会顺着这个列表自左向右地依次尝试满足它们. 根据这个规则, 此处首先需要完成的目标就是 f(_G34), 也就是 “我需要一个满足性质 f 的项”. 而基于此目标在知识库中执行自上而下的搜索, Prolog 首先查询到的, 可以与该目标联合的项就是 f(a). 经过与 f(a) 的联合, 变量 _G34 被实例化为 a, 第一个目标得到满足. 因此我们有:

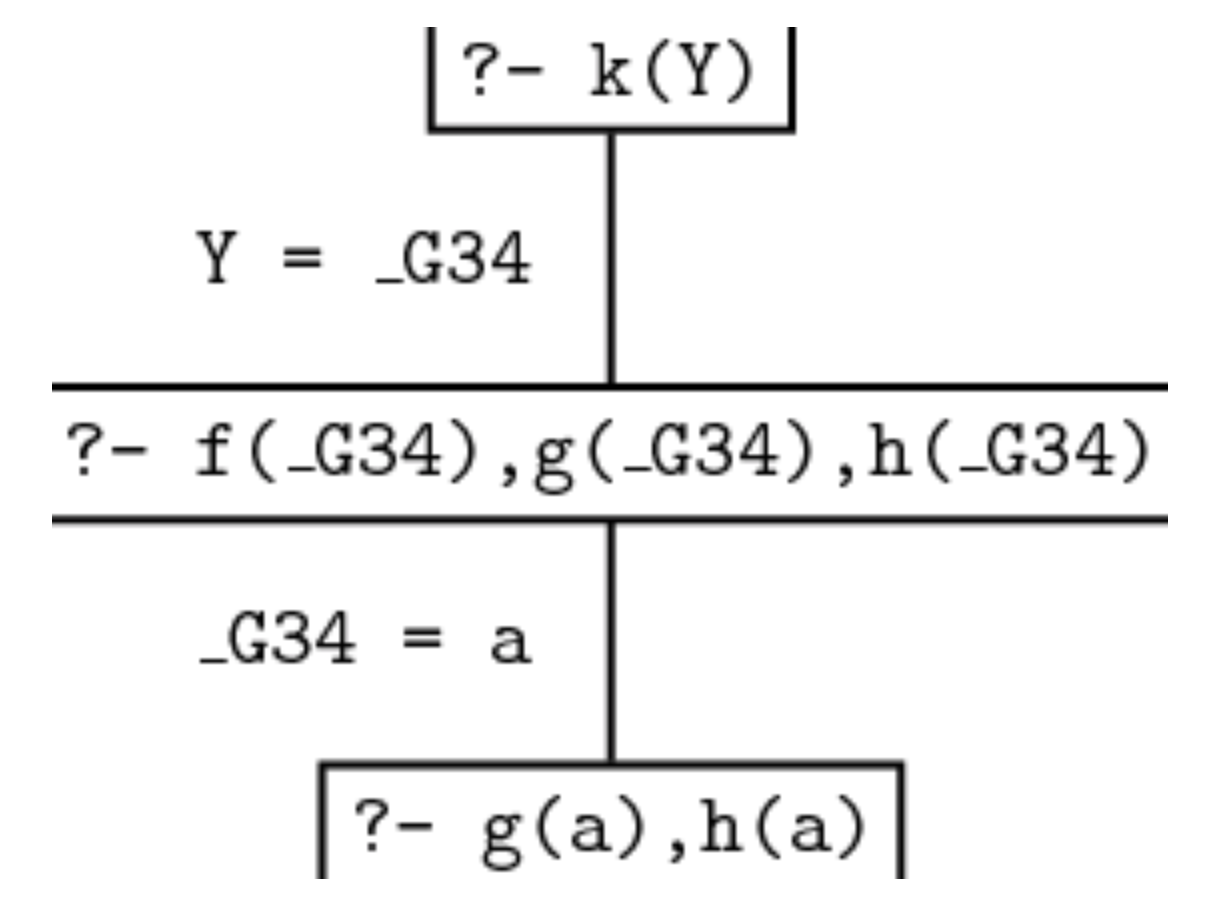
将目标切换为 g(a), 重复上述流程可得, 知识库中事实 g(a) 可与目标联合. 故此时有

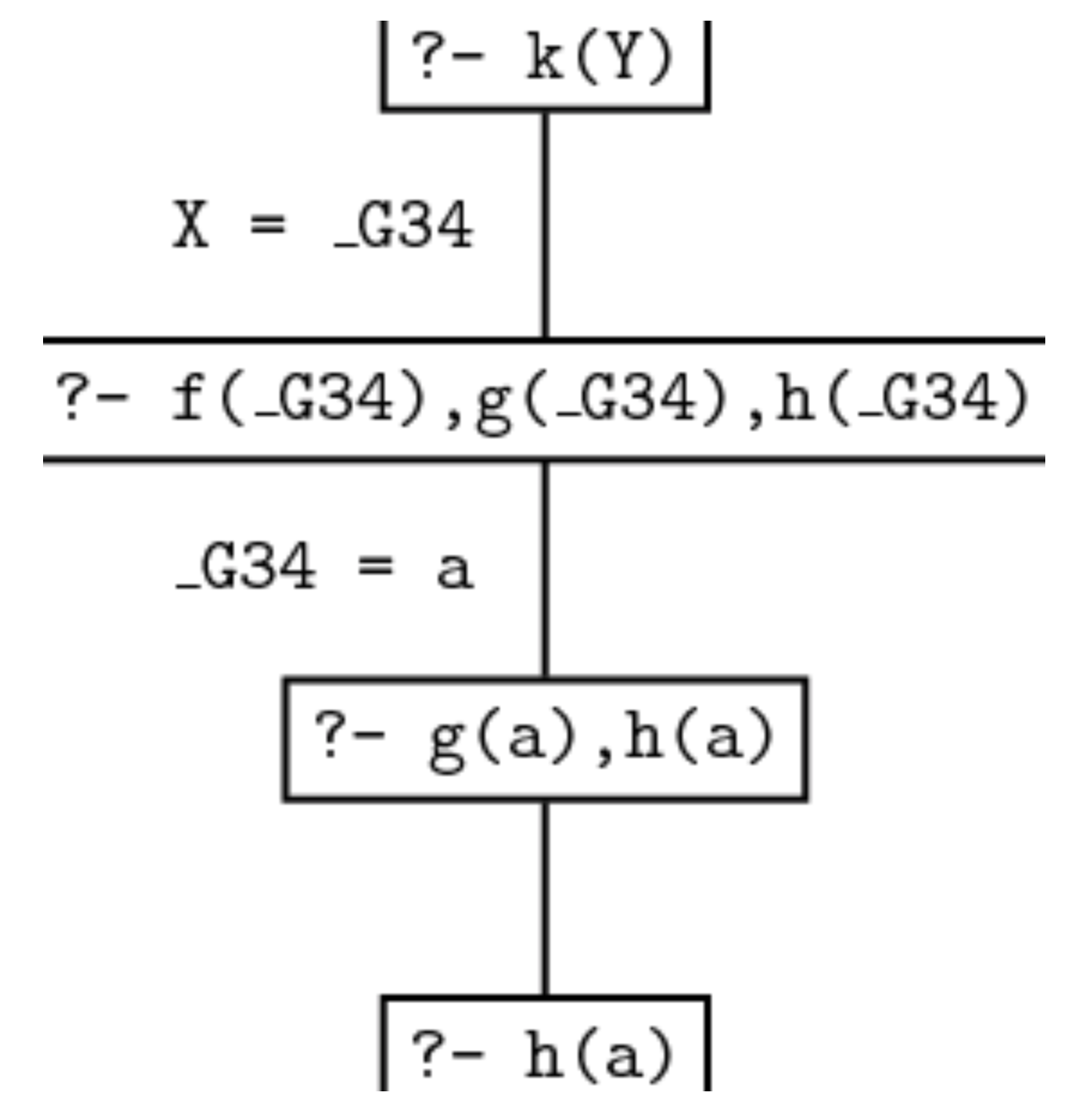
但将目标再切换为 h(a), 经过检索无法在知识库中找到任何可以与目标联合的项.

此时, Prolog 会将该情况判定为 “选择错误”, 并且回头检查是否在上一轮对旧事实的联合中能够找到另一种解法, 这一过程也就是在求解树上的回溯 Backtrack. 由于 Prolog 在求解过程中会记录所有的决策点 (也就是记录了决策过程中需要依次满足的每一个目标, 并且记录了每一步中选择了知识库中的哪一条规则), 因此如果无法求解, Prolog 可以沿着决策树依次回溯直到原点. 在此处的例子中, 我们最终回溯到原点, 在此处我们需要满足下列目标:

1
f(_G34),g(_G34),h(_G34).

由于在上次检索中首先联合了事实 f(a), 故此次换用事实 f(b) 与第一个目标联合. 执行上文中描述的搜索过程, 此次我们就可以最终发现, h(b) 可以与知识库中完全相同的事实相联合, 故目标列表中的全体都可被满足. 并且, 由于在该过程中 Y 被实例化为 b, Prolog 也记录下了满足目标的方法.

此时我们输入 ; 就可以查询是否存在其他解. 虽然在本例中显然这样的解不存在. 但是如果还有其他的事实可供尝试的话, Prolog 会重新执行一遍沿知识库自顶而下, 沿目标列表自左而右的检索流程.

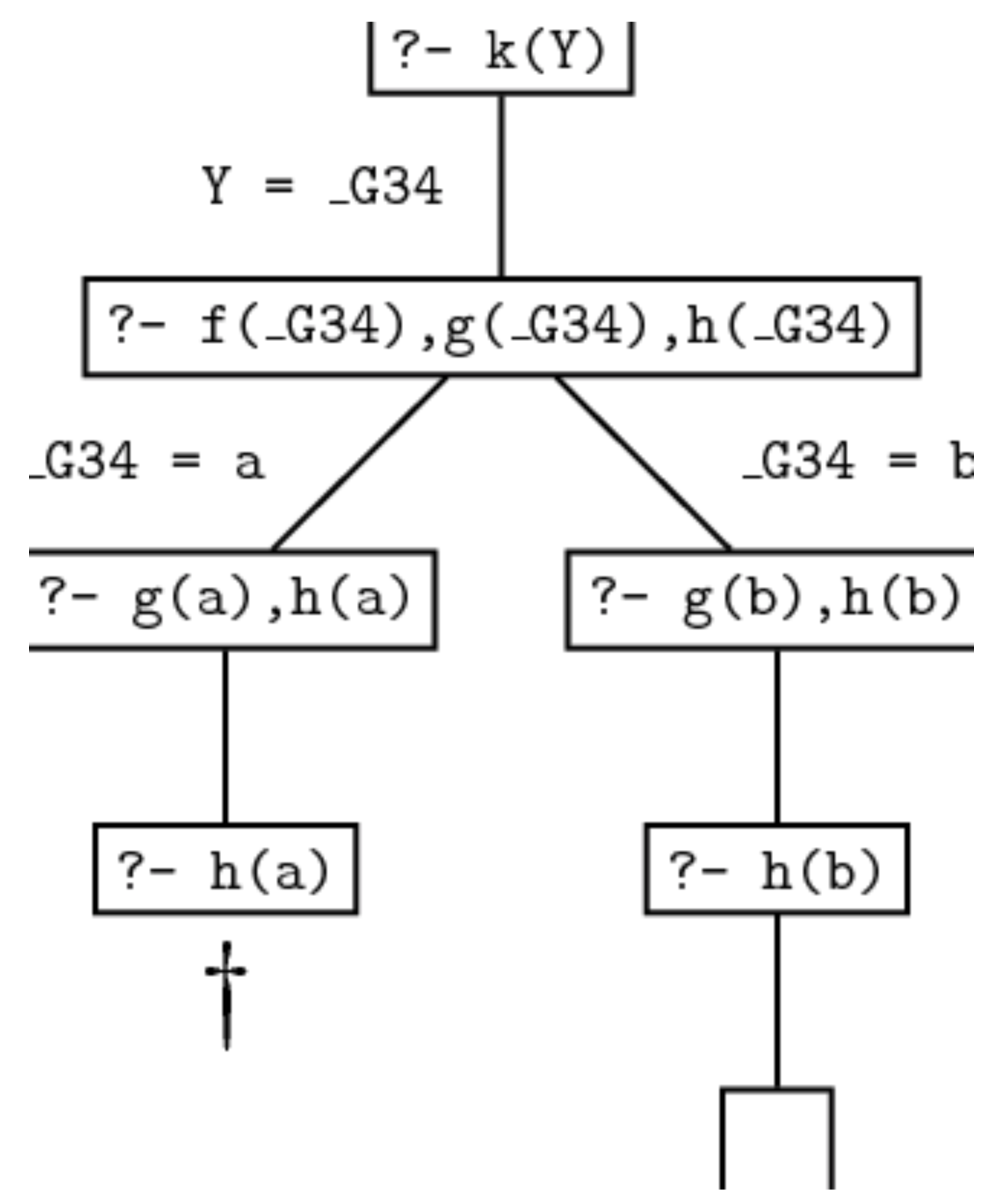
最后, 我们欣赏一下 Prolog 解决该问题时所生成的决策树:

• Previous
  Prolog 学习 Ch1
• Next
  Prolog 学习 Ch3