4. While 语法及其状态描述
在本章中, 我们将引入结构简单的 While 语法, 作为我们在接下来的章节中所将要介绍和学习的诸多概念的载体. 我们将对该语法本身, 使用该语法构造简单程序的方法流程及使用 状态 和 正则语义 对使用该语法构造的程序的执行状态的描述方法进行详细介绍:
While 程序语法
程序语法本质上是对我们所希望计算机执行的操作的一种描述方法. 为了让程序完全按照我们的设想执行, 程序语法必须是 无歧义 (Unambiguous) 的. 下面, 我们对 While 程序语法进行定义:
对于该语法, 我们分别定义了 陈述 (Statements), 布尔表达式(Boolean Expression) 和 运算表达式(Arithmetic Expression).
为了确保该语法的简易性, 我们仅在语法定义中给出了部分基本的程序组成元素, 但使用这些基本的组成元素已经足以让我们将语法的功能按需扩展.
如: 该语法缺失了
\[\text{if} ~...~ \text{then}~...~\]语句. 而为了实现它, 我们只需对语法所提供的
\[\text{if} ~...~ \text{then}~...~ \text{else} ~...~\]语句进行简单修改, 因为:
\[[\text{if} ~b~ \text{then}~S~] \equiv [\text{if} ~b~ \text{then}~S~ \text{else} ~\text{skip}~].\]我们可以这样对语法中其他缺失的语句和特性进行定义.
描述 While 程序执行状态
我们下面对该程序语义的 状态 进行定义:
定义 (状态)
我们称 状态 为一个从变量映射到整数的函数: \(\text{State} = \text{Var} \rightarrow \mathbb{Z}.\)
我们使用符号 $\sigma$ 表示 状态.
例:
定义
\[\sigma = [x \rightarrowtail 5, y\rightarrowtail 7, z\rightarrowtail 0]\]则有
\[\sigma(x) = 5, \sigma(y) = 7.\]注意: 我们认为一切变量的默认值均为 $0$, 因此 $\sigma$ 又等价于
\[[x \rightarrowtail 5, y\rightarrowtail 7].\]定义 (改变状态)
我们使用方括号作为 状态修改符号.
例:
令
\[\sigma' = \sigma[x \rightarrowtail v]\]则有
\[\sigma'(x) = v\]且对 $\forall~ y \neq x:$
\[\sigma'(y) = y.\]我们下面对状态更新语法进行描述:
定义如下记号
\[<~S~, ~\sigma~>\]其中, $S$ 为一个使用 $\text{while}$ 语法的程序, 而 $\sigma$ 为某个状态. 下表描述了状态转换规则:
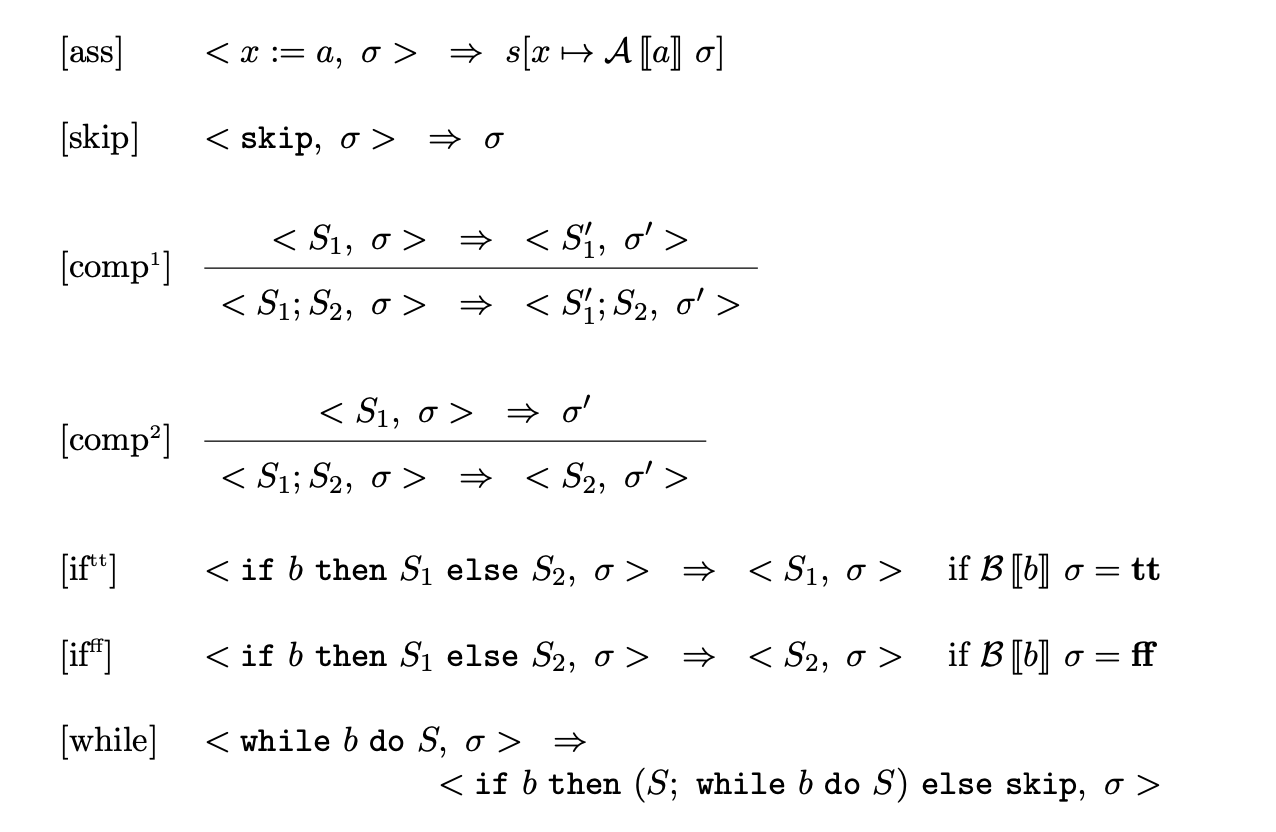
其中对 $\mathscr{A}$ 和 $\mathscr{B}$ 的定义分别如下:

它们的实质是对 数值运算 和 布尔表达式 在某个状态 $\sigma$ 下的 解释 (Interpretation).
使用上表中的状态转换规则, 我们可以描述使用 $\text{while}$ 语法的程序的每一步运行状态. 如:
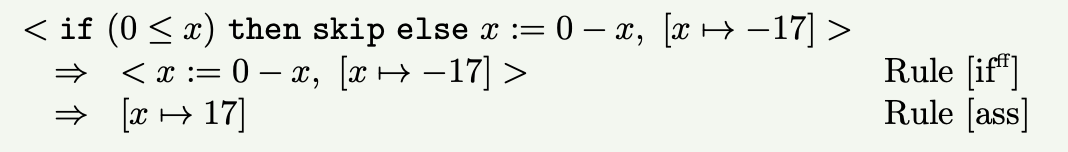
构造简单数据结构
我们接下来研究如何将有限的数据结构编码到自然数中. 这意味着对于给定的数据结构, 我们需要定义一个从它到自然数集的双射. 这样, 我们对数据结构的操作可以体现为某个自然数的变化, 而给定任何自然数, 我们也可以基于该映射得出它所被编码的内容.
首先, 我们考虑 整数. 考虑如下函数:
\[\beta(x) = \begin{cases} 2x ~~~~~~~~~~~~~~~~x \geq 0 \\ -2x-1 ~~~~~~\text{else}\end{cases}\]它将所有非负整数映射到偶数上, 而将负整数映射到奇数上. 并且不难证明, 这个函数是双射.
我们再研究 数对. 考虑如下函数:
\[\phi(n, m) = 2^n(2m+1)-1.\]不难看出, 该函数将任意不同的数对 $(n, m)$ 映射到不同的整数上, 并且它也是双射.
我们最后考虑 列表. 由于几乎所有的数据结构都可以被表示成数对和列表的组合, 在完成对 列表 的构造后, 我们就具备了构造复杂数据结构的基础.
我们首先回顾对 列表 的递归定义:
\[\text{list} = [] ~~\vert~~ n:: \text{list}\]其中, $n$ 为任意自然数, $[]$ 为某个空列表, 而 $::$ 为链接符, 表示将自然数 $n$ 连接到某个列表的表头.
我们给出如下的递归定义:
\[\begin{aligned}\Phi([]) =& 0 \\ \Phi(n :: l) =& 2^n(2\Phi(l) + 1) = \phi(n, \Phi(l)) + 1.\end{aligned}\]