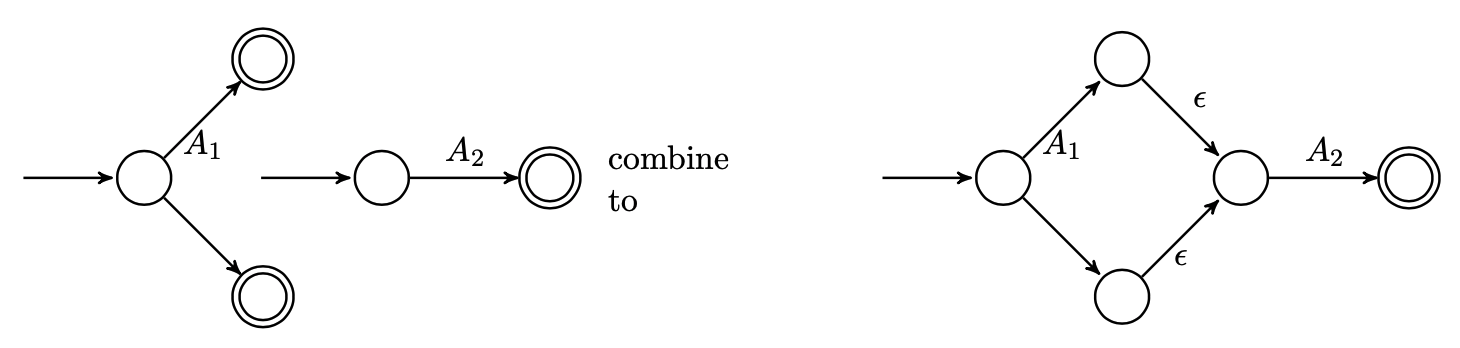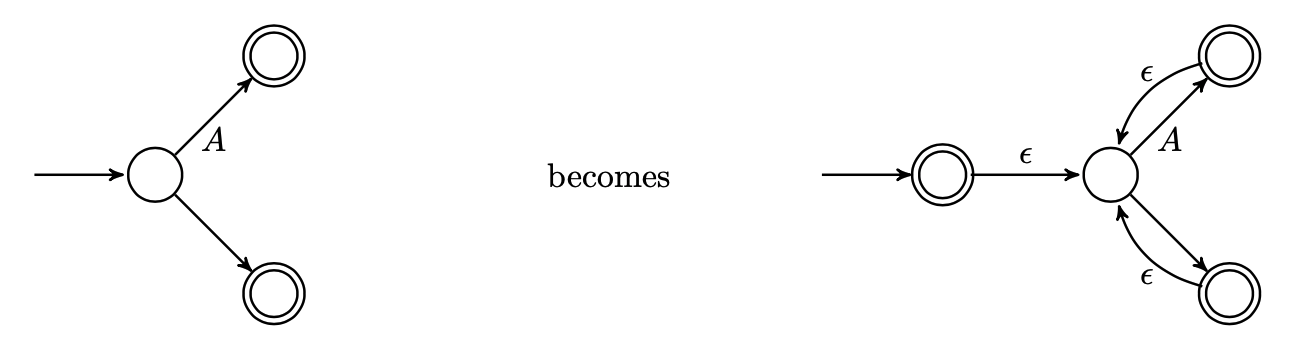自动机

本章介绍不同种类的自动机 (Automata), 并介绍多个实现在自动机和模式 (正则表达式) 之间进行转换的算法:

1. 有限状态自动机 Finite State Automata

在上一学期的课程中我们已经接触到了有限状态机, 以及有限状态机的状态转换图. 我们首先对有限状态机的定义进行回顾:

定义2.1.1 有限状态机

任何有限状态机均有下列元素所组成:

• 数个状态
• 一个起始态 (Initial State)
• 数个可接受态 (Accepting State, 可以是 $0$ 个)
• 与字母表 $\Sigma$ 中每一个字母 $x$ 一一对应的转换关系, 其接受 $x$ 为条件, 并以此将状态从某一个转换为另外一个.

注: 对 转换关系 的正规化定义如下:

定义2.1.2 转换函数

我们称从集合 \(Q \times \Sigma = \{(q, x) \vert q \in Q, x \in \Sigma \}\) 接受输入, 并以某个状态作为输出的函数为 状态转换函数, 记号为 $\delta$.

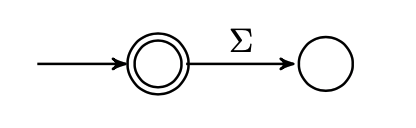
下面我们规定在状态转换图中表示起始状态与终止状态 (可接受态) 的记号和方法:

我们使用一个单箭头, 将单箭头所指向的状态标记为起始态; 我们使用双圆环标记状态转换图中的所有可接受态.

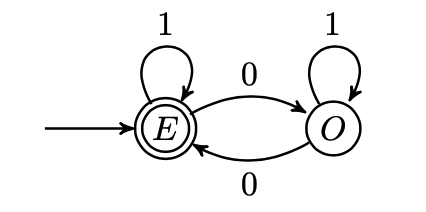
下图为一个在字母表 ${0, 1}$ 上过滤出所有以 $010$ 结尾的文字的有限状态机的状态转换图.

2. 确定性有穷自动机 Deterministic Finite Automata

确定性有穷自动机有时也被简称为 有限状态机, 其核心特征为基于给定条件的状态转换始终唯一. 其定义如下:

定义2.2.1 确定性有穷自动机

基于字母表 $\Sigma$ 的确定性有穷自动机由以下元素组成:

• 状态集 $Q$, 有限非空.
• 起始状态 $q_{\cdot}$, $q_{\cdot} \in Q$.
• 可接受态集 $F$, $F \subset Q$.
• 状态转换函数 $\delta$:
  

\[\begin{aligned}\delta: &Q \times \Sigma \rightarrow Q \\ &q \rightarrowtail ^{x}q' \end{aligned}\]

其中 $^{x}q’$ 表示以输入 $x$ 为条件, 从状态 $q$ 将要转换到的目标状态.
一般地, 我们用一个四元组 $(Q, q_{\cdot}, F, \delta)$ 表示一个确定性有穷自动机.

定义2.2.2 被确定性有穷自动机所接受的文字

称文字 $s = x_1x_2\cdots x_n$ 被确定性有穷自动机 $(Q, q_{\cdot}, F, \delta)$ 接受 (Accepted), 若:

\[\begin{cases}\begin{aligned}&\delta(q_{\cdot}, x_i) = q_1 ~~~~~~\text{for} ~~ \forall x \in [n]\\&q_n \in F \end{aligned}\end{cases}.\]

空文字 $\epsilon$ 当且仅当该确定性有穷自动机的起始状态为一个可接受态时被该自动机所接受.

进一步地:

定义2.2.3 被确定性有穷自动机所接受的语言

称某一语言被某个确定性有穷自动机所 接受 (recognized), 当且仅当该语言中的所有文字均被自动机所接受.

3. 非确定性有穷自动机 Non-deterministic Finite Automata

非确定性有穷自动机与确定性有穷自动机相反, 其核心特征为基于给定条件的状态转换可能不唯一. 其定义如下:

定义2.3.1 非确定性有穷自动机

基于字母表 $\Sigma$ 的非确定性有穷自动机由以下元素组成:

• 状态集 $Q$, 有限非空.
• 起始状态 $q_{\cdot}$, $q_{\cdot} \in Q$.
• 可接受态集 $F$, $F \subset Q$.
• 状态转换 关系 $\delta$:
  

\[\begin{aligned}\delta: &Q \times \Sigma\rightarrow Q\\&q \rightarrowtail ^{x}q'\end{aligned}\]

其中 $^{x}q’$ 表示以输入 $x$ 为条件, 从状态 $q$ 将要转换到的目标状态, 这样的目标状态可以是不唯一的, 因此我们在此不称 $\delta$ 为函数, 而称其为 关系.
一般地, 我们用一个四元组 $(Q, q_{\cdot}, F, \delta)$ 表示一个非确定性有穷自动机.

定义2.3.2 被非确定性有穷自动机所接受的文字

称文字 $s = x_1x_2\cdots x_n$ 被非确定性有穷自动机 $(Q, q_{\cdot}, F, \delta)$ 接受 (Accepted), 若: 存在状态链

\[q_0, q_1, \cdots, q_n\]

其中 $q_0 = q_{\cdot}$, 且 $(q_i, x_i) \rightarrow_{\delta} q_{i+1}$, $q_n \in F$.

进一步地:

定义2.2.3 被非确定性有穷自动机所接受的语言

称某一语言被某个非确定性有穷自动机所 接受 (recognized), 当且仅当该语言中的所有文字均被自动机所接受.

4. 非确定性有穷自动机 $\rightarrow$ 确定性有穷自动机的转换算法

定义2.3.1 和定义2.2.1 间有很明显的包含关系. 下述定理阐明了这一关系:

定理2.4.1

对任何一个非确定性有穷自动机, 恒存在一个确定性有穷自动机与之等价.

下面, 我们考虑非确定性有穷自动机到确定性有穷自动机的转换方法.

算法1 非确定性有穷自动机 - 确定性有穷自动机转换算法

1. 对给定非确定性有穷自动机各个状态进行编号.
2. 从起始状态开始:
   • 枚举基于每一个可能的条件可以到达的所有的新状态$s_1, s_2, \cdots, s_n$.
   • 将这些新状态整合为同一个自定义的新状态, 记为 $s_1s_2\cdots s_n$.
   • 检查新状态 $s_1s_2\cdots s_n$ 的可接受性: 若 $s_1, s_2, \cdots, s_n$ 中至少有一个可接受态, 则将$s_1s_2\cdots s_n$ 也标记为可接受态.
   • 持续遍历所有的状态链, 直到不可再继续遍历. 此时所生成的有穷自动机即为所要求的确定性有穷自动机.

通过对非确定性有穷自动机 $(Q, q_{\cdot}, F, \delta)$ 应用 算法1, 我们所得到的确定性有穷自动机满足如下特征:

• 其状态集为 $Q$ 的幂集
• 其起始状态和原自动机的一致
• 该确定性有穷自动机的任一状态 $S$ 是可接受态, 当且仅当 $\exists q \in S, q \in F$.

• 该确定性有穷自动机的可接受态集定义为:
  

  \[F' = \{q' \in Q \vert \exists q \in S ~~ \text{with} ~~ q \in F\}.\]

• 对于新状态 $S \in \mathscr{P}(Q)$ 和字母 $x \in \Sigma$，给定条件 $x$, 可转换到:
  

  \[\{q' \in Q \vert \exists q \in S ~~ \text{with} ~~ q \rightarrow^x q'\}.\]

我们称这样的确定性有穷自动机为 由非确定性有穷自动机 $(Q, q_{\cdot}, F, \delta)$ 生成的确定性有穷自动机.

5. 自动机 $\rightarrow$ 表达式的转换算法

本节我们研究从确定性有穷状态机到正则表达式的转换算法.

算法2 确定性有穷自动机 - 正则表达式转换算法

• 首先按照各个状态的复杂度对其进行先后编号
• 下面对问题进行分治:
  • 将问题基于最终到达的可接受态的不同而分成数个不同的子问题
  • 对每一个子问题, 再分别基于可行的路径所会经过的中间态的不同对其进行二度分治
• 解决所有的子子问题后我们可以得到数个不同的可行语言描述 (也就是路径描述)
• 将其取并可得到与DFA对应的语言的集合化描述
• 将集合描述转化为正则表达式描述, 即得到所要求的正则表达式.

一般地:
将自动机的状态记为 ${0, 1, \cdots, n}$, 并将起始态记为 $j$, $0 \leqslant j \leqslant n$. 因此, 在语言 $\mathscr{L}$ 中, 所有被自动机所接受的文字可表为该集合:

\[\bigcup_{i \in F} \mathscr{L}_{j \rightarrow i} = \bigcup_{i \in F} \mathscr{L}_{j \rightarrow i}^{\leqslant n}\]

其中, $\mathscr{L}_{j \rightarrow i}$ 为 所有在 “以 $j$ 为起始态, $i$ 为可接受终止态” 这一边界条件下, 通过自动机的状态转换所得到的文字的集合 (语言).

实际上, \(\mathscr{L}_{j \rightarrow i},\)$\mathscr{L}_{j \rightarrow i}^{\leqslant n}$ 是等价的, 也就是 所有在 “以 $j$ 为起始态, $i$ 为可接受终止态, 并且经过的状态编号最大不超过 $n$” 这一边界条件下, 通过自动机的状态转换所得到的文字的集合 (语言). 我们在这个思想的指导下就可以进一步地对状态判定进行分治.

我们可以逐次将边界条件中 ”经过的状态编号最大不超过 $k$“ 中的 $k$ 从 $n$ 递减至 $0$, 并依次求出对应边界条件下自动机所有可能经由的状态转换列, 并将其表示出来.

而在考虑边界条件 “以 $j$ 为起始态, $i$ 为可接受终止态, 并且经过的状态编号最大不超过 $k$” 时, 我们可以将问题进一步划分为两个部分: 遵循条件 “经过的状态编号最大不超过 $k-1$” 的情形

以及遵循条件 先经过多个编号最大不超过 $k-1$的状态从 $i$ 到达 $k$, 然后再任意次经过多个编号最大不超过 $k-1$ 的状态原地打转, 再最终经过一些编号小于等于 $k-1$ 的状态到达可接受终止态 $i$ 的情形.

也就是:

\[\mathscr{L}_{j \rightarrow i}^{\leqslant k} = \mathscr{L}_{j \rightarrow i}^{\leqslant k-1} \cup \mathscr{L}_{j \rightarrow k}^{\leqslant k-1} \cdot (\mathscr{L}_{k \rightarrow k}^{\leqslant k-1})^{\star} \cdot \mathscr{L}_{k \rightarrow i}^{\leqslant k-1}.\]

而对每一条路径, 在将其对应的不同可行语言描述取并时, 有:

\[\mathscr{L}^{\leqslant -1}_{i \rightarrow i} = \begin{cases} \{\epsilon\} ~~~~~~~~~~~~~~~~~~~~~~ \text{if no transition from i to i} \\ \{\epsilon, x_1, x_2,\cdots\} ~~~ x_i ~\text{are all labels on the transition from i to i} \end{cases}\] \[\mathscr{L}^{\leqslant -1}_{j \rightarrow i} = \begin{cases} \{\emptyset\} ~~~~~~~~~~~~~~~~~~~~~~ \text{if no transition from j to i} \\ \{x_1, x_2,\cdots\} ~~~~~~~ x_i ~\text{are all labels on the transition from j to i} \end{cases}\]

这也就是 算法2 中的第三步.

我们有以下的两个结论:

定理2.5.1

任何确定性有穷自动机均可被转换为某个正则表达式.

定理2.5.2

任何确定性或非确定性有穷自动机所接受的语言都是正则的.

6. 表达式 $\rightarrow$ 自动机的转换算法

要从正则表达式转换到某个有穷自动机, 我们需要先将正则表达式转换为含空转换的非确定性有穷自动机, 然后可以将其转换为确定性有穷自动机, 也可以再进一步地转换为确定性有穷自动机. 为了实现正则表达式到自动机的转换, 我们首先需要引入一系列新概念:

定义2.6.1 含空转换的非确定性有穷自动机

定义 $\Sigma$ 为不包含 $\epsilon$ 的字母表. 基于 $\Sigma$ 的, 含空转换的非确定性有穷自动机 为一个定义在 $\Sigma$ 上的, 可能以 $\epsilon$ 作为某些状态的转换条件的非确定性有穷自动机.

定义2.6.2 被含空转换的非确定性有穷自动机接受的文字

称字母表 $\Sigma$ 上的文字 $x_1x_2\cdots x_n$ 被含空转换的非确定性有穷自动机 $(Q, q_{\cdot}, F,\sigma)$ 所接受, 若存在状态链
\(q_0 = q_{\cdot}, q_1, \cdots q_l\) 且
对于 $\forall i \in [n]$:

\[q_{m_i-1} \rightarrow^{\epsilon} q^{1}_{m_i + 1} \rightarrow^{\epsilon} \cdots \rightarrow^{\epsilon} q_{m_i - 1} \rightarrow^{x_i} q_{m_i}\]

并且

\[q_{m_n} \rightarrow^{\epsilon} q^{1}_{m_{n} + 1}\rightarrow^{\epsilon} \cdots \rightarrow^{\epsilon} q_{l}\]

并规定 $m_0 = 0$, 因此 $q_l$ 为一个可接受态. 注意在此处任何一个从 $m_i-1$ 到 $m_i+1$ 的状态转换都可能完全不经过任何以空文字 $\epsilon$ 为条件的中间状态转换.

定义2.6.3 被含空转换的非确定性有穷自动机所接受的语言

称由所有被含空转换的非确定性有穷自动机所接受的文字组成的集合为 被含空转换的非确定性有穷自动机所接受的语言.

下面我们介绍将正则表达式转换为含空转换的非确定性有穷自动机的算法:

算法3 正则表达式至含空转换的非确定性有穷自动机转换算法

我们使用如下的递归转换将正则表达式转换为含空转换的非确定性有穷自动机:

• 模式 $\emptyset$ 由下图定义:
  

• 模式 $\epsilon$ 由下图定义:
  
• 模式 $x, x\in \Sigma$ 由下图定义:
  

• 连接 (Concatenation) 由下图定义:
  下图所示的状态转换分别为接受 $p_1, p_2$ 的状态转换. 在此我们将 $A_1$ 的全部可接受态转为不可接受态, 并用 $\epsilon$ 连接至 $A_2$ 的起始态. 在 $A_1$ 只有一个可接受态时, 则直接将其可接受态剔除, 连接到 $A_2$ 的起始态而无需额外的 $\epsilon$ 连接.
  

• 取并 (Alternative) 由下图定义:
  下图所示的状态转换分别为接受 $p_1, p_2$ 的状态转换. 我们新建一个中间态, 并将其同时用 $\epsilon$ 连接到 $A_1$ 和 $A_2$, 从而生成接受 $p_1 \vert p_2$ 的状态转换.
  
• 克莱尼星号:
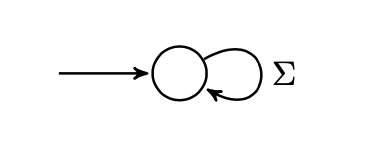
  我们使用如下的方式表示克莱尼星号: 给定自动机 $A$，首先引入一个新的可接受态作为起始状态, 并将其用 $\epsilon$ 连接到原来的起始态, 再将原图中所有的可接受态用 $\epsilon$ 连接到原先的起始态.
  
  需要注意的是, 在转换克莱尼星号时切勿忘记引入新的起始态 (用于表示克莱尼星号中的 $\epsilon$).

在使用 算法3 将正则表达式转换为含空转换的非确定性有穷自动机后, 我们往往还需要将其再转换为非确定性有穷自动机. 我们下面介绍将含空转换的非确定性有穷自动机转为非确定性有穷自动机的转换法:

算法4 含空转换的非确定性有穷自动机至非确定性有穷自动机转换算法

• 将所有可通过空条件转化为可接受态的不可接受态转为可接受态.
• 从原始的 $\epsilon-\text{NFA}$ 中保留所有含非空条件的转换态.
• 将含有空条件和非空条件的混合转换态简化(我们可以略过从起始状态由空条件转换到的所有中间态, 而只去考虑由非空条件而转换到的最终态): 如果某状态可以通过数个空条件以及 最后 的一个非空条件转换到另一状态, 则在图中添加一个直接由该非空条件, 从原状态转换至另一状态的转换关系.
• 最后从状态转换图中删去所有不可达态, 即得到所要求的非确定性有穷自动机.

一般地, 给定含空转换的非确定性有穷自动机 $(Q, q_{\cdot}, F, \delta)$, 我们如下定义它的 (不含空转换的) 非确定性有穷自动机:

• 令 \(F' = F\cup \{q \in Q \vert \exists q = q_0, \cdots, q_n \in Q ~\text{with}~ q_i \rightarrow^{\epsilon} q_{i+1} ~\text{for}~ \forall i \in [n-1] ~\text{and}~ q_n \in F \}.\) 换言之, 这是 算法4 第一步的数学定义.

• 设 $q, q’ \in Q, ~x \in \Sigma$. 规定 $\delta’$ 将 $(q, x)$ 关联至 $q‘$ 当且仅当存在状态列
  

  \[q = q_1, q_2, \cdots, q_n = q'\]

  使得
  

  \[q = q_1 \rightarrow^{\epsilon} q_2 \cdots q_{n-2} \rightarrow^{\epsilon} q_{n-1} \rightarrow^{x} q_n = q'.\]

  这是 算法4 第三步的数学定义.

  
  

  通过使用 算法3 和 算法4, 我们实现了从正则表达式到非确定性有穷状态机的转换. 我们可以进一步使用 算法1 将其转换为确定性有穷自动机.

  
  

  基于上述算法, 我们可以得到如下结论:

  定理2.6.1

  对任意一个含空转换的非确定性有穷状态机, 恒存在一个与之等价的 (不含空转换的) 非确定性有穷状态机.

  
  

  定理2.6.2

  对任意的正则表达式, 我们都可以将其转换为:

  • 确定性有穷状态机
  • 非确定性有穷状态机
  • 含空转换的非确定性有穷状态机
    

  且它们在描述符号化语言上具有同等效力.

  
  

7. 正则语言的一般性质

下面我们介绍正则语言的一些基本性质.

• 正则语言的正则性对 连接运算, 克莱尼星号 以及 取反运算 等封闭. 也就是说:

定理2.7.1 正则性质的封闭特性

设 $\mathscr{L_1}, \mathscr{L2}$ 为正则语言, 且分别被正则表达式 $p_1, p_2$ 所定义. 则:

• 对它们取连接运算所得的新语言也是正则的.
• 对它们中的任何一个作克莱尼星号运算所得的新语言也是正则的.
• 对它们中的任何一个作取反运算所得的新语言也是正则的.
• 对它们中的任何一个作取并运算所得的新语言也是正则的.
• 对它们中的任何一个作取交运算所得的新语言也是正则的.
• 对它们中的任何一个作取补运算所得的新语言也是正则的.

我们定义 “取反运算”:

定义2.7.1 取反 (Reversal)

设文字 $s$ 定义于字母表 $\Sigma$ 上. 则对其进行取反运算后得到的新文字是将其从后往前遍历所得到的结果:

下面我们考虑如何使用自动机表示经过上述运算后所得到的新语言.

对于取连接运算, 立即有:

\[\mathscr{L_1} \cdot \mathscr{L_2} = \mathscr{L}(p_1)\cdot \mathscr{L}(p_2) = \mathscr{L}(p_1p_2)\]

对于作克莱尼星号运算, 有:

\[\mathscr{L^{\star}}\]

对于取反运算, 有:

\[\mathscr{L}^{R} = \{x_nx_{n-1}\cdots x_{2}x_{1} ~ \vert ~ x_1x_2\cdots x_{n-1}x_{n} \in \mathscr{L}\}.\]

对于取并运算, 有:

\[\mathscr{L_1} \cup \mathscr{L_2}\]

并且上述的四种运算所对应的自动机表述已经在前一节的 算法3 中说明.

下面我们考虑 交运算 和 取补运算 的自动机表述:

交运算的自动机表述远不如上述的几种运算一样直观. 为了满足交运算指定的限制条件, 也就是该自动机能且只能过滤出同时属于两种语言中的文字, 我们不能再简单地将两个自动机拼接在一起, 而要设法在执行文字过滤时, 同时在两个自动机中执行状态转移.

要实现这一目标, 我们需要结合原有的两个自动机 $(Q_1, q_{\cdot}^{1}, F_1, \delta_1), (Q_2, q_{\cdot}^{2}, F_2, \delta_2)$ , 创建一个新的:

• 这个新的自动机的状态集将是 $Q_1 \times Q_2$
• 其起始态将是 $(q_{\cdot}^{1}, q_{\cdot}^{2}).$
• 其可接受集将是 $F_1 \times F_2$.
• 其状态转换关系 $\delta$ 将是一个将状态 $(q_1, q_2)$ 在以 $x$ 为转换条件的前提下映射至 $(q_1’, q_2’)$ 的函数.

我们称这一自动机为 两个自动机的乘积.

而补运算是指, 若 $\mathscr{L}$ 为定义在字母表 $\Sigma$ 上的语言, 则它的补被定义为 $\Sigma^{\star} - \mathscr{L}$. 也就是, 所有定义在字母表上, 而不属于该语言的文字.

8. 自动机的等价性

我们知道, 同样的正则表达式可以被不同的自动机所等价描述. 在一些情形下, 确定两个自动机之间的等价性是很重要的, 这一节我们研究解决两个 确定性有穷自动机 的等价性的问题.

回顾定义, 我们认为接受相同语言的自动机就是等价的, 无论它是非确定性状态机还是确定性状态机. 在最简单的情况下, 如果两个自动机除了编号和标记有所区别的话, 我们可以立即判定出这两个自动机的等价性. 而对于更为复杂的情况, 我们也有解决的方法.

首先介绍使用补运算和交运算判定两个自动机的等价性的方法:

该方法的原理是应用下列结论:

\[\begin{aligned} \mathscr{L} = \mathscr{L'} ~~~~&\text{iff} ~~~~ \mathscr{L}\subseteq \mathscr{L'} ~ \text{and} ~ \mathscr{L'} \subset \mathscr{L} \\ &\text{iff} ~~~~ \mathscr{L} \cap (\Sigma^{\star} - \mathscr{L'} = \emptyset) ~\text{and}~ \mathscr{L'} \cap (\Sigma^{\star} - \mathscr{L}) = \emptyset. \end{aligned}\]

而要应用这一方法, 需要我们首先计算两次自动机的补, 再计算两次自动机的并, 最后将其与 $\emptyset$ 比较. 从计算量上看, 这一方法并不实际.

我们再介绍另一个方法: 通过 “模拟” 确定, 对于第一个自动机的每一个状态所可能的每一个下一步转换, 另一个自动机中都有一个状态与之等价, 从而证明两个自动机所接受的语言是相同的.

定义2.8.1 自动机的等价

定义关系 $\sim$ 为任意两个自动机 $A: (Q, q_{\cdot}, F, \delta), B: (P, p_{\cdot}, E, \gamma)$ 之间的 模拟 (Simulation), 当且仅当:

• \[q_{\cdot} \sim p_{\cdot}\]
• \[\begin{aligned} \text{if} ~ q \sim p &~\text{for some } ~ q \in Q, p \in P ~ \text{then} \\ &-~\text{if} ~ q \rightarrow^{x} q', ~ \text{then} ~ \exists ~ p' \in P, ~\text{s.t.} ~ p \rightarrow^{x} p' ~\text{and}~ q' \sim p'. \\ &-~q \in F ~ \text{implies}~ p \in E.\end{aligned}\]

并且有以下的结论确保 “模拟” 的可行性:

命题2.8.1

若存在一个从某个非确定性有穷自动机到另一个的 “模拟”, 则任何被第一个自动机所接受的文字必同样被第二个所接受. 因此可以确定, 第一个自动机所接受的语言是第二个的子集.

定理2.8.2

设 $A, B$ 为任两个非确定性有穷自动机. 若存在一个从 $A$ 到 $B$ 的 “模拟”, 并且反方向的 “模拟” 同样存在, 则 $A$ 所接受的语言和 $B$ 相同.

对于确定性有穷自动机, 我们还有更强的结论:

命题2.8.2

设 $A, B$ 为任两个确定性有穷自动机. 若 $A$ 所接受的语言是 $B$ 的子集, 则必存在一个从 $A$ 到 $B$ 的 “模拟”.

定理2.8.3

设 $A, B$ 为任两个确定性有穷自动机. $A$ 所接受的语言和 $B$ 相同, 当且仅当 存在一个从 $A$ 到 $B$ 的 “模拟”, 并且反方向的 “模拟” 同样存在.

需要注意的是, “存在一个从 $A$ 到 $B$ 的 “模拟”, 并且反方向的 “模拟” 同样存在” 对于 NFA 而言只是 必要不充分 条件, 而对于 DFA 则是 充要条件.

我们还观察到, 许多确定性有穷自动机是可以被进一步简化的. 通过比对两个自动机的最简化形式, 也可以判断出它们的等价性.

定理2.8.4 自动机最简化定理 (Minimalization)

对任何确定性有穷自动机 $A$, 我们总能找到它的最简形式 $M$, 满足:

• $M$ 与 $A$ 等价.
• 对任何其他与 $A$ 等价的自动机 $B$, $B$ 的状态数量恒大于等于 $M$ 的.

换言之, 在不考虑编号差异的情况下, $M$ 是唯一的.

下面我们介绍一种计算某个确定性有穷自动机最简形式的算法 - 填表算法 (Table Filling Algorithm):

在介绍该算法之前, 我们给出对于状态的 可分别性 的定义:

定义2.8.2 状态的可分别性 (Distinguishable)

记 $A = (Q, q_{\cdot}, F, \delta)$ 为一个定义在 $\Sigma$ 上的确定性有穷自动机. 对其任两个状态 $p, q \in Q$: 我们称它们是 可分别的, 若:

• $p \in F, q \notin F ~\text{or vice versa, or:}~$
• $\exists ~ x \in \Sigma, \delta(p, x) ~ \text{is disginguishable from } ~ \delta(q, x).$

换言之, 在检查两个状态是否具有可分别性时, 我们只需要检查:

• 它们的可接受性是否相同?
• 以它们为某个转换的起始状态, 是否能基于完全相同的条件, 转换到完全相同的新状态?

算法5 填表算法

填表算法的流程很简单:

• 为要检查的确定性有穷自动机的所有状态编号.
• 构造一个以所有编号作为行与列的表格.
• 不考虑对角线上方的所有状态对 (任何状态与其自身一定不可区分, 无需考虑), 并判定剩下的每一个状态对的可分别性.
• 若所有的状态对都是可分别的, 则说明该自动机已经是最简的.
• 若存在至少一对不可分别的状态对, 则将其简化.
• 在简化完所有的, 不可分别的状态对后, 所得到的自动机即为输入自动机的最简形式.

在本章中, 我们介绍了使用 有穷自动机 描述正则语言的方法, 并解释了不同种类自动机与正则语言之间的转换算法. 此外, 我们还介绍了自动机等价性的定义和判断方法, 并介绍了正则语言的一般性质. 在下一章中, 我们将继续探究对复杂语言的表述方法, 介绍 上下文无关语法, 以及 巴克斯 - 诺尔范式 .

---

• Previous
  Ch1 计算理论 语言和正则表达式
• Next
  Ch3 计算理论 表述复杂语言

---