卷积神经网络
卷积神经网络的结构和之前所介绍的神经网络相似, 都可以通过对不同层的组合实现网络的构建. 在卷积神经网络中, 我们新引入了 卷积 (Convolution) 层和 池化 (Pooling) 层.
在详细介绍卷积层和池化层的原理与实现之前, 我们首先简述通过组装层构建 CNN 的方法. 对于常规的神经网络而言, 连接层可以用 Affine 层实现, 而激活函数层中可以使用 ReLU 函数, 在最后的输出层中, 激活函数可以选用 SoftMax 函数.
而对卷积神经网络而言, 其层的连接顺序是: 卷积层 - 激活函数层 (如 ReLU 层) - 可省略的池化层, 如下图所示:

使用全连接层的神经网络会丢弃输入数据的维度信息. 无论作为数据集的原始数据先天具有何种维度 (如三维的图像) , 它都将被统一转换为一维数据, 由此丢失了一些可能对学习而言至关重要的空间信息. 相比之下, 卷积层可以保持输入数据的维度信息不变. 当输入数据为具有三个维度的图像时, 卷积层会以三维数据的形式接收它, 并以同样的维度输出至下一层. 因此, 卷积神经网络相比常规的全连接神经网络更有可能正确理解和提炼出图像等多维数据中隐藏的信息.
在卷积神经网络中, 卷积层的输入输出数据又称为 特征图 (Feature Map), 卷积层的输入数据称为 输入特征图 (Input Feature Map), 其输出数据称为 输出特征图 (Output Feature Map).
1. 卷积层和池化层
卷积层中所进行的运算即为 卷积运算.
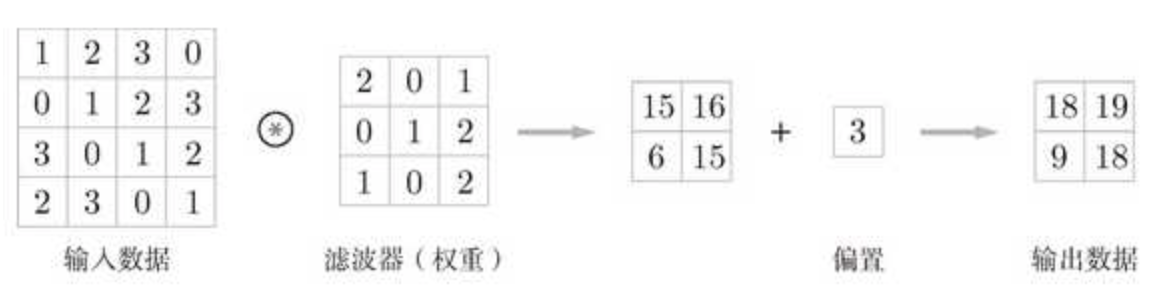
卷积运算涉及两个变量. 其一是作为输入的原始数据, 一般是一个较大的高维矩阵. 其二是卷积核 (也称 “滤波器” ), 即一个小于原始数据的矩阵. 在计算过程中, 我们将从原始数据中剥离出和卷积核维度一致的子矩阵 (我们也可以将卷积核看作叠加在原始数据之上的 “窗口”, 将剥离过程视为 “窗口的滑动”), 并将其和卷积核进行矩阵乘法, 再将所得矩阵中所有元素的值相加, 即完成一次卷积计算, 得到一个值, 它将作为输出矩阵中的一个元素. 按照给定的 “滑动步长” (步幅, stride) , 将卷积核从原始数据矩阵的左上角继续移动, 每一次移动均进行一次卷积计算, 直到卷积核矩阵的右下角到达原始数据矩阵的右下角, 计算终止. 而通过计算卷积核横向移动的步长和卷积核在滑动过程中 “换行” 的次数, 我们可以得出输出矩阵的维度.
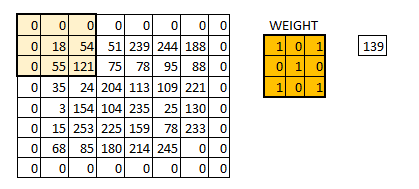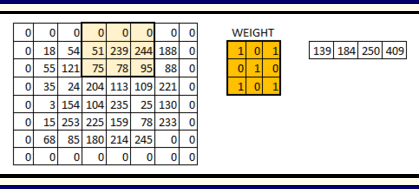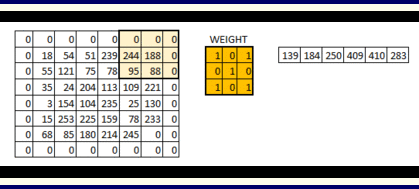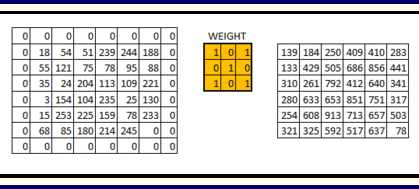
在计算卷积运算的偏置时, 只需将偏置分别加到输出矩阵的每一个元素上即可:
填充 (Padding) 是一种常用的, 面向输入数据的处理方法:
卷积运算中的 填充处理 就是向输入数据的周围填入 $0$, 从而改变输入数据的维度. 这一操作的目的主要是调整输出的大小. 如果对维度为 $4, 4$ 的输入数据应用步长为 $1$, 维度为 $3, 3$ 的卷积核, 所得到的输出数据维度为 $2, 2$. 为了避免在多次卷积运算中输出数据维度不断缩减导致最终缩减为 $1, 1$ 以致于无法再对其应用卷积运算, 我们可以对输入数据施加幅度为 $1$ 的填充使其维度变为 $5, 5$, 这样的话输出维度就会和输入维度保持一致.
下面我们考虑三通道数据 ($3$ 维数据) 的卷积运算:
三维数据的卷积运算在多出的纵深方向上增加了相应的特征图. 在纵深方向上有多个特征图时, 还会按通道方向进行输入数据和卷积核之间的卷积运算.
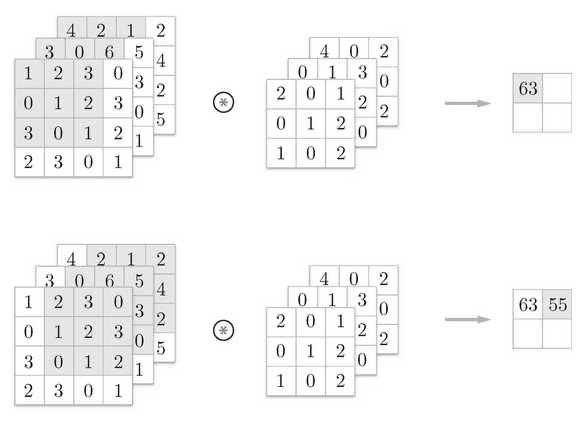
在 $3$ 维数据的卷积运算中, 输入数据的通道数和卷积核的通道数应保持一致.
池化就是缩小数据在长和高方向上大小的运算. 如下图所示, 通过使用 Max 池化, 我们将 $2*2$ 的数据范围集约为 $1$ 个元素的数据处理, 我们缩小了空间大小.
Max 池化是获取最大值的运算, 在上图所示的运算中, 我们选定的目标区域大小是 $2*2$. 此外, 我们还将步幅设为了 $2$. 一般而言, 我们将池化窗口大小和步幅设为相同的值.
池化方法除了 Max 池化外, 还有 Average (均值) 池化, Stochastic (随机) 池化, Median (中值) 池化等.
池化层具有以下特点:
- 和卷积层不同, 池化只是从目标区域中取最值, 池化层没有需要学习的参数.
- 池化运算的计算是按照通道而独立进行的, 因此池化运算并不会改变输出数据和输入数据的通道数.
- 一般而言, 在输入数据发生微小偏差时, 池化仍然会返回相同的结果. 这一特性也被称为池化运算的 健壮性.
2. 卷积层与池化层的实现
下面我们进行卷积层和池化层的实现 (处理 $3$ 维数据) :
在 CNN 中, 各层间传递的数据维度为 $4$: 数据数量, 数据高, 数据长, 数据通道数.
1
2
3
4
x = np.random.rand(10, 1, 28, 28)
//the 1st data: x[0]
//the 1st data's 1st channel data: x[0][0]
为提高运算效率, 我们使用 im2col 函数实现卷积运算.
img2col 是一个可以将输入数据展开以使其适应卷积核的函数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
filter_h : 滤波器的高
filter_w : 滤波器的长
stride : 步幅
pad : 填充
Returns
-------
col : 2维数组
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
下面使用该函数实现卷积层.
卷积层的初始化方法接收 卷积核(权重), 偏置, 步幅和填充. 滤波器为 $(\text{FN}, \text{C}, \text{FH}, \text{FW})$ 的四维形状. 这四个参数分别为: Filter Number, Channel, Filter Height, Filter Width.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
def forward(self, x):
FN, C, FH. FW = self.W.shape
N, C, H, w = x.shape
out_h = int(1 + (H + 2*self.pad-FH) / self.stride)
out_w = int(1 + (w + 2*self.pad-FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out
和卷积层相同, 池化层也使用 im2col 展开输入数据. 但对于池化而言, 其数据展开在通道方向上是独立的.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
return out
